1 Introduction
The concept of coherent structures in wall-bounded flows probably originated with Theodorsen (Reference Theodorsen1952). It was soon associated with the phenomenon of bursting, which was first observed in turbulent boundary layers by Kline et al. (Reference Kline, Reynolds, Schraub and Runstadler1967) as an oscillation and breakdown of what were later recognised to be streaks of low streamwise velocity. Both have received continuing attention since then because they are locally strong events that promise, up to a point, an independent evolution from the rest of the flow. They make chaotic turbulence appear ‘simpler’. It was not initially clear whether the intermittency observed in experiments was due to measurement artefacts or to true temporally recurrent motions. The temporal analysis of direct numerical simulations (DNS) of boundary layers by Robinson (Reference Robinson1991), and later of minimal flows in the buffer (Jiménez & Moin Reference Jiménez and Moin1991) and logarithmic layers (Flores & Jiménez Reference Flores and Jiménez2010) of channels, showed that the experimentally observed bursts are passing intense structures, but that these structures grow and wane over longer periods of the order of their turnover time (Jiménez et al. Reference Jiménez, Kawahara, Simens, Nagata and Shiba2005). More recently, visual inspection has begun to be substituted by automatic machine processing, allowing the spatial and temporal characterisation of bursting structures in full-scale channels at reasonably high Reynolds numbers (Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014). The structural point of view has become an indispensable and complementary method to statistics, and the two are often blended together (Jiménez Reference Jiménez2013b ).
Streaks are created by the interaction of the wall-normal velocity with the shear (Bakewell & Lumley Reference Bakewell and Lumley1967; Kim & Lim Reference Kim and Lim2000; Jiménez Reference Jiménez2013a ), and they are known to form even in the absence of walls (Uzkan & Reynolds Reference Uzkan and Reynolds1967; Lee, Kim & Moin Reference Lee, Kim and Moin1990). Bursting appears to require more restrictive conditions. The simplest shear flow is unbounded homogeneous shear turbulence (HST), which, unfortunately, does not have an asymptotic statistically stationary state. Ideal HST in unbounded domains grows indefinitely, both in intensity and in length scale (Champagne, Harris & Corrsin Reference Champagne, Harris and Corrsin1970; Harris, Graham & Corrsin Reference Harris, Graham and Corrsin1977; Lee et al. Reference Lee, Kim and Moin1990; Kida & Tanaka Reference Kida and Tanaka1994), and simulations are typically discontinued as the growing length scale approaches the size of the computational box (Rogers & Moin Reference Rogers and Moin1987). However, Pumir (Reference Pumir1996) extended the simulation to longer times and reached a statistically stationary state (SSHST) in which the largest-scale motion is constrained by the computational box and undergoes a succession of growth and decay phases of the kinetic energy and the enstrophy, reminiscent of the bursts in wall-bounded flows. This suggests that bursting is also a common feature of shear-induced turbulence, but that it requires the restriction of the structures before growth can be reinitiated. In SSHST, this restriction is due to the numerical box. In wall-bounded turbulence, it is presumably due to the wall or, when simulated in a small box, to the constrained spanwise direction (Flores & Jiménez Reference Flores and Jiménez2010). It should be noted that this implies that any simulation of SSHST is minimal, especially in the spanwise direction (Sekimoto, Dong & Jiménez (Reference Sekimoto, Dong and Jiménez2016), SDJ16 from now on), and that its largest scales are not necessarily representative of those of unbounded HST.
Nevertheless, previous investigators have found that the growth rates of the kinetic energy during bursts in SSHST and in the logarithmic layer of minimal channels are very similar, and that their growth phase is qualitatively the same as in the initial shearing of isotropic turbulence (Pumir Reference Pumir1996; Gualtieri et al. Reference Gualtieri, Casciola, Benzi, Amati and Piva2002). Indeed, SDJ16 showed that the evolution of the flow during all the phases of the SSHST bursts is similar to that in wall turbulence, undergoing lift-up, instability, breakdown and regeneration. Statistics, such as the two-point correlation of the vertical velocity, also agree well between both flows (SDJ16).
The purpose of this paper is to study the coherent flow structures in SSHST, compare them with those in turbulent channels, and study their behaviour in a simpler setting than wall turbulence. In particular, by comparing the structures in the two flows, we seek to distinguish which features are dominated by the wall and which ones are general properties of shear-driven turbulence. For the sake of brevity, we will refer from now on to statistically stationary homogeneous shear turbulence simply as HST.
One of the best-studied characterisations of bursting is based on the quadrant analysis introduced by Wallace, Eckelman & Brodkey (Reference Wallace, Eckelman and Brodkey1972) and Willmarth & Lu (Reference Willmarth and Lu1972). If
![]() $u$
and
$u$
and
![]() $v$
are the streamwise and wall-normal velocity fluctuations, Reynolds-stress
$v$
are the streamwise and wall-normal velocity fluctuations, Reynolds-stress
![]() $(uv)$
events can be classified into Q1s (
$(uv)$
events can be classified into Q1s (
![]() $u>0,v>0$
), Q2s (ejections,
$u>0,v>0$
), Q2s (ejections,
![]() $u<0,v>0$
), Q3s (
$u<0,v>0$
), Q3s (
![]() $u<0,v<0$
) and Q4s (sweeps,
$u<0,v<0$
) and Q4s (sweeps,
![]() $u>0,v<0$
). The co-gradient Q2s and Q4s, with
$u>0,v<0$
). The co-gradient Q2s and Q4s, with
![]() $uv<0$
, will be collectively denoted as Q
$uv<0$
, will be collectively denoted as Q
![]() $^{-}$
s, while the counter-gradient Q1s and Q3s are Q
$^{-}$
s, while the counter-gradient Q1s and Q3s are Q
![]() $^{+}$
s. Coherent Qs are defined as specially intense
$^{+}$
s. Coherent Qs are defined as specially intense
![]() $(uv)$
events, classified in terms of their quadrant. Early investigators found that approximately 70 % of the total Reynolds stress in a turbulent boundary layer is contained in those Q
$(uv)$
events, classified in terms of their quadrant. Early investigators found that approximately 70 % of the total Reynolds stress in a turbulent boundary layer is contained in those Q
![]() $^{-}$
s that are strong enough to be easily distinguishable from the rest of the flow (Kim, Kline & Reynolds Reference Kim, Kline and Reynolds1971; Lu & Willmarth Reference Lu and Willmarth1973), and Qs soon came to be considered as one of the best burst indicators in terms of one-point measurements (Bogard & Tiederman Reference Bogard and Tiederman1986). More recently, Qs have been extended to three-dimensional objects by Lozano-Durán, Flores & Jiménez (Reference Lozano-Durán, Flores and Jiménez2012, LFJ12 hereafter), who later studied their temporal evolution (Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014). It is interesting that, although the thresholds used in these papers to define strong structures were determined in a very different way from experiments, they turned out to be very similar to those in previous papers, giving some support to the idea that ‘strong’ Qs have objective significance. LFJ12 found that Qs can be divided into readily distinguishable families of wall-attached and detached structures according to whether their minimum distance from the wall is below or above
$^{-}$
s that are strong enough to be easily distinguishable from the rest of the flow (Kim, Kline & Reynolds Reference Kim, Kline and Reynolds1971; Lu & Willmarth Reference Lu and Willmarth1973), and Qs soon came to be considered as one of the best burst indicators in terms of one-point measurements (Bogard & Tiederman Reference Bogard and Tiederman1986). More recently, Qs have been extended to three-dimensional objects by Lozano-Durán, Flores & Jiménez (Reference Lozano-Durán, Flores and Jiménez2012, LFJ12 hereafter), who later studied their temporal evolution (Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014). It is interesting that, although the thresholds used in these papers to define strong structures were determined in a very different way from experiments, they turned out to be very similar to those in previous papers, giving some support to the idea that ‘strong’ Qs have objective significance. LFJ12 found that Qs can be divided into readily distinguishable families of wall-attached and detached structures according to whether their minimum distance from the wall is below or above
![]() $y^{+}\approx 20$
. Using the term in that sense, attached Q
$y^{+}\approx 20$
. Using the term in that sense, attached Q
![]() $^{-}$
s are the dominant structures from the point of view of momentum transfer. Bursting Qs have recently been associated with the linearised transient Orr (Reference Orr1907) amplification mechanism by Jiménez (Reference Jiménez2013a
, Reference Jiménez2015).
$^{-}$
s are the dominant structures from the point of view of momentum transfer. Bursting Qs have recently been associated with the linearised transient Orr (Reference Orr1907) amplification mechanism by Jiménez (Reference Jiménez2013a
, Reference Jiménez2015).
Also associated with bursting in wall-bounded flows are hairpin vortices (Theodorsen Reference Theodorsen1952; Perry & Chong Reference Perry and Chong1982), although mostly observed at relatively low Reynolds numbers, near the wall or in transition (Head & Bandyopadhyay Reference Head and Bandyopadhyay1981; Acarlar & Smith Reference Acarlar and Smith1987; Zhou et al. Reference Zhou, Adrian, Balachandar and Kendall1999; Adrian Reference Adrian2007). The interest in hairpins is largely due to their simple shape, which makes them easy to visualise as triggers of bursts. The two legs of a hairpin are quasi-streamwise vortices that move low-velocity fluid away from the wall to create streaks that eventually become unstable and break down. In this sense, hairpins are models for the Q2s described in the previous paragraph. A different kind of vortical structure was studied by del Álamo et al. (Reference del Álamo, Jiménez, Zandonade and Moser2006, AJZM06 from now on), who examined three-dimensional connected vortex clusters defined by the discriminant of the velocity-gradient tensor in the logarithmic layer of channels at relatively high Reynolds number. They found a self-similar hierarchy of structures fitting the attached-eddy model of Townsend (Reference Townsend1961). As in the case of Qs, vortex clusters separate into wall-attached and detached families, but, although the averaged flow field of an attached vortex cluster contains a long conical low-speed streamwise-velocity ‘wake’ reminiscent of streaks, headed by a shorter pair of ejections, the instantaneous shapes are irregular and very different from hairpins. The question of whether hairpin vortices persist in high-Reynolds-number wall-bounded turbulence, and of whether they should be understood as instantaneous structures (Wu & Moin Reference Wu and Moin2009; Schlatter et al. Reference Schlatter, Li, Örlü, Hussain and Henningson2014) or as conditional statistical constructs (AJZM06; Tanahashi et al. Reference Tanahashi, Kang, Miyamoto and Shiokawa2004; Flores & Jiménez Reference Flores and Jiménez2006; Jiménez Reference Jiménez2013b ), remains controversial, and is the subject of much current debate.
Streaks, Qs and vortical structures are not unrelated to each other. On average, Q2s and Q4s in channels form spanwise pairs located at the interface between high- and low-velocity streaks. The flow field conditioned to these pairs includes a central longitudinal large-scale roller (LFJ12; Jiménez Reference Jiménez2013b ), reminiscent of the average arrangement of streaks and quasi-streamwise vortices in the buffer layer (Robinson Reference Robinson1991; Jiménez & Pinelli Reference Jiménez and Pinelli1999; Schoppa & Hussain Reference Schoppa and Hussain2002). Vortex clusters are also located on average between the two Qs, closer to the Q2. Whether the quasi-streamwise roller is an averaged reflection of these vortex clusters is unclear, and will be one of the questions considered in this paper. Similarly, it is also unknown whether hairpins are connected with the structure just described.
Another question to be addressed is the relation between wall-attached and detached structures. Most of the properties mentioned above apply mostly to attached Qs and clusters. Hairpins have also been considered mostly in relation to the wall, although Rogers & Moin (Reference Rogers and Moin1987) found that hairpin vortices, or at least hairpin vortex lines, exist in HST, and Vanderwel & Tavoularis (Reference Vanderwel and Tavoularis2011) found both ‘upright’ and ‘inverted’ hairpins in experimental HST, distinct enough to be made visible as concentrations of hydrogen bubbles. In wall-bounded flows, detached Qs tend to be small and isotropic, and do not carry net Reynolds stress. LFJ12 showed that structures with similar properties are found in free-shear flows, including flows with no mean shear. Even if it appears natural to compare eddies in HST with detached ones in wall turbulence, the difference between attached and detached structures has to be clarified and will be examined in this paper.
In fact, the distinction between the two families is not absolute. There are large detached structures in wall-bounded turbulence, although very large ones tend to hit the wall and become attached. Structures that are detached at a given threshold may be attached at lower ones, and, when Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) examined the temporal evolution of Qs and vortex clusters in channels, they found that a given structure may start life as detached only to later attach to the wall, and vice versa.
The similarities and differences between the statistics of HST and wall turbulence have been examined by Pumir (Reference Pumir1996), Gualtieri et al. (Reference Gualtieri, Casciola, Benzi, Amati and Piva2002) and SDJ16, but, as far we are aware, the relationship between their three-dimensional structure has not been studied in any detail.
The rest of the paper begins by introducing the database in § 2. The identification method used to extract coherent structures is detailed in § 3, followed in § 4 by the description of their geometric and flow characteristics, including comparisons with channels. Their spatial organisation is studied in § 5, followed in § 6 by the conditionally averaged flow fields in their neighbourhood. The paper closes with discussion and conclusions.
2 Numerical experiments
Throughout this paper,
![]() $x$
and
$x$
and
![]() $z$
are respectively the streamwise and spanwise directions, and
$z$
are respectively the streamwise and spanwise directions, and
![]() $y$
is the (vertical) coordinate in the direction of the mean shear. The corresponding velocities are
$y$
is the (vertical) coordinate in the direction of the mean shear. The corresponding velocities are
![]() $\hat{u}$
,
$\hat{u}$
,
![]() ${\hat{w}}$
and
${\hat{w}}$
and
![]() $\hat{v}$
. Upper-case symbols are used for mean values averaged over time and over all the homogeneous directions of the flow, as in
$\hat{v}$
. Upper-case symbols are used for mean values averaged over time and over all the homogeneous directions of the flow, as in
![]() $\unicode[STIX]{x1D6F7}=\langle \hat{\unicode[STIX]{x1D719}}\rangle$
. Fluctuations with respect to those averages are in lower case,
$\unicode[STIX]{x1D6F7}=\langle \hat{\unicode[STIX]{x1D719}}\rangle$
. Fluctuations with respect to those averages are in lower case,
![]() $\unicode[STIX]{x1D719}=\hat{\unicode[STIX]{x1D719}}-\unicode[STIX]{x1D6F7}$
, and root-mean-squared (r.m.s.) intensities are denoted by primes, as in
$\unicode[STIX]{x1D719}=\hat{\unicode[STIX]{x1D719}}-\unicode[STIX]{x1D6F7}$
, and root-mean-squared (r.m.s.) intensities are denoted by primes, as in
![]() ${\unicode[STIX]{x1D719}^{\prime }}^{2}=\langle \unicode[STIX]{x1D719}^{2}\rangle$
. Occasionally, the coordinates and velocities are represented by subscripts in the range
${\unicode[STIX]{x1D719}^{\prime }}^{2}=\langle \unicode[STIX]{x1D719}^{2}\rangle$
. Occasionally, the coordinates and velocities are represented by subscripts in the range
![]() $x\ldots z$
, in which case repeated indices imply summation. This is always the case for the vorticities
$x\ldots z$
, in which case repeated indices imply summation. This is always the case for the vorticities
![]() $\unicode[STIX]{x1D714}_{i}$
. The time-dependent average over the homogeneous directions of a fluctuating quantity
$\unicode[STIX]{x1D714}_{i}$
. The time-dependent average over the homogeneous directions of a fluctuating quantity
![]() $\unicode[STIX]{x1D719}$
is denoted by
$\unicode[STIX]{x1D719}$
is denoted by
![]() $\overline{\unicode[STIX]{x1D719}}(t)$
. If
$\overline{\unicode[STIX]{x1D719}}(t)$
. If
![]() $S=\,\text{d}U/\,\text{d}y$
is the mean shear, the friction velocity is defined as
$S=\,\text{d}U/\,\text{d}y$
is the mean shear, the friction velocity is defined as
![]() $u_{\unicode[STIX]{x1D70F}}^{2}=|\unicode[STIX]{x1D708}S-\langle uv\rangle |$
in HST and as
$u_{\unicode[STIX]{x1D70F}}^{2}=|\unicode[STIX]{x1D708}S-\langle uv\rangle |$
in HST and as
![]() $u_{\unicode[STIX]{x1D70F}}^{2}=\unicode[STIX]{x1D708}|S_{w}|$
in channels, where
$u_{\unicode[STIX]{x1D70F}}^{2}=\unicode[STIX]{x1D708}|S_{w}|$
in channels, where
![]() $S_{w}$
is the shear at the wall and
$S_{w}$
is the shear at the wall and
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity. Quantities in the wall units defined by
$\unicode[STIX]{x1D708}$
is the kinematic viscosity. Quantities in the wall units defined by
![]() $u_{\unicode[STIX]{x1D70F}}$
and
$u_{\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D708}$
are denoted by the superscript ‘
$\unicode[STIX]{x1D708}$
are denoted by the superscript ‘
![]() $+$
’. The dimensions of the simulation boxes are
$+$
’. The dimensions of the simulation boxes are
![]() $L_{x}$
,
$L_{x}$
,
![]() $L_{y}$
and
$L_{y}$
and
![]() $L_{z}$
. Lengths in channels are normalised with the half-height
$L_{z}$
. Lengths in channels are normalised with the half-height
![]() $h=L_{y}/2$
, and the buffer, logarithmic and outer layers are defined as
$h=L_{y}/2$
, and the buffer, logarithmic and outer layers are defined as
![]() $y^{+}<100$
,
$y^{+}<100$
,
![]() $100\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}<y<0.2h$
and
$100\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}<y<0.2h$
and
![]() $y>0.2h$
respectively.
$y>0.2h$
respectively.
The code for the HST simulations is described in detail in SDJ16. It integrates the time evolution of the vertical vorticity
![]() $\unicode[STIX]{x1D714}_{y}$
and of the Laplacian of
$\unicode[STIX]{x1D714}_{y}$
and of the Laplacian of
![]() $v$
. The numerical domain is periodic in
$v$
. The numerical domain is periodic in
![]() $x$
and
$x$
and
![]() $z$
, with boundary conditions in
$z$
, with boundary conditions in
![]() $y$
that enforce periodicity between uniformly shifting points at the upper and lower boundaries. The spatial discretisation is dealiased Fourier spectral in the two periodic directions, and compact finite differences with spectral-like resolution in
$y$
that enforce periodicity between uniformly shifting points at the upper and lower boundaries. The spatial discretisation is dealiased Fourier spectral in the two periodic directions, and compact finite differences with spectral-like resolution in
![]() $y$
(Lele Reference Lele1992). The shifting boundary condition in
$y$
(Lele Reference Lele1992). The shifting boundary condition in
![]() $y$
avoids the periodic remeshing required by tilting-grid codes (Rogallo Reference Rogallo1981) and most of their associated enstrophy loss (SDJ16).
$y$
avoids the periodic remeshing required by tilting-grid codes (Rogallo Reference Rogallo1981) and most of their associated enstrophy loss (SDJ16).
Table 1. Simulation parameters for the three DNS of HST used in this paper. Here,
![]() $Re_{\unicode[STIX]{x1D706}}$
is the Reynolds number based on the Taylor microscale;
$Re_{\unicode[STIX]{x1D706}}$
is the Reynolds number based on the Taylor microscale;
![]() $A_{xz}$
and
$A_{xz}$
and
![]() $A_{yz}$
are the box aspect ratios;
$A_{yz}$
are the box aspect ratios;
![]() $\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}$
,
![]() $\unicode[STIX]{x0394}y/\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x0394}y/\unicode[STIX]{x1D702}$
and
![]() $\unicode[STIX]{x0394}z/\unicode[STIX]{x1D702}$
are the average resolutions in terms of the Kolmogorov scale
$\unicode[STIX]{x0394}z/\unicode[STIX]{x1D702}$
are the average resolutions in terms of the Kolmogorov scale
![]() $\unicode[STIX]{x1D702}$
, with their standard deviations due to intermittency;
$\unicode[STIX]{x1D702}$
, with their standard deviations due to intermittency;
![]() $\unicode[STIX]{x0394}x$
and
$\unicode[STIX]{x0394}x$
and
![]() $\unicode[STIX]{x0394}z$
are computed from the number of Fourier modes before dealiasing;
$\unicode[STIX]{x0394}z$
are computed from the number of Fourier modes before dealiasing;
![]() $L_{c}$
is the Corrsin scale;
$L_{c}$
is the Corrsin scale;
![]() $\unicode[STIX]{x1D70E}_{u}/u^{\prime }$
is the ratio of the r.m.s. of
$\unicode[STIX]{x1D70E}_{u}/u^{\prime }$
is the ratio of the r.m.s. of
![]() $[\overline{u^{2}}(t)]^{1/2}$
to the r.m.s. of the point-wise fluctuations of
$[\overline{u^{2}}(t)]^{1/2}$
to the r.m.s. of the point-wise fluctuations of
![]() $u$
, with similar definitions for
$u$
, with similar definitions for
![]() $\unicode[STIX]{x1D70E}_{v}/v^{\prime }$
and
$\unicode[STIX]{x1D70E}_{v}/v^{\prime }$
and
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6F1}}/\unicode[STIX]{x1D6F1}^{\prime }$
, where
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6F1}}/\unicode[STIX]{x1D6F1}^{\prime }$
, where
![]() $\unicode[STIX]{x1D6F1}$
is the second invariant of the velocity-gradient tensor. The two channels used for comparison are included for reference, with properties given at
$\unicode[STIX]{x1D6F1}$
is the second invariant of the velocity-gradient tensor. The two channels used for comparison are included for reference, with properties given at
![]() $y/h\approx 0.4$
, where
$y/h\approx 0.4$
, where
![]() $Re_{\unicode[STIX]{x1D706}}$
is maximum.
$Re_{\unicode[STIX]{x1D706}}$
is maximum.

The simulations are characterised by three dimensionless parameters: the streamwise and vertical aspect ratios of the simulation domain,
![]() $A_{xz}=L_{x}/L_{z}$
and
$A_{xz}=L_{x}/L_{z}$
and
![]() $A_{yz}=L_{y}/L_{z}$
, and the Reynolds number
$A_{yz}=L_{y}/L_{z}$
, and the Reynolds number
![]() $Re_{z}=SL_{z}^{2}/\unicode[STIX]{x1D708}$
. We also use the Corrsin (Reference Corrsin1958) shear parameter
$Re_{z}=SL_{z}^{2}/\unicode[STIX]{x1D708}$
. We also use the Corrsin (Reference Corrsin1958) shear parameter
![]() $S^{\ast }=Sq^{2}/\unicode[STIX]{x1D700}$
and the Reynolds number
$S^{\ast }=Sq^{2}/\unicode[STIX]{x1D700}$
and the Reynolds number
![]() $Re_{\unicode[STIX]{x1D706}}=q^{2}(5/3\unicode[STIX]{x1D708}\unicode[STIX]{x1D700})^{1/2}$
based on the Taylor microscale
$Re_{\unicode[STIX]{x1D706}}=q^{2}(5/3\unicode[STIX]{x1D708}\unicode[STIX]{x1D700})^{1/2}$
based on the Taylor microscale
![]() $\unicode[STIX]{x1D706}=q(5\unicode[STIX]{x1D708}/\unicode[STIX]{x1D700})^{1/2}$
, where
$\unicode[STIX]{x1D706}=q(5\unicode[STIX]{x1D708}/\unicode[STIX]{x1D700})^{1/2}$
, where
![]() $q^{2}=\langle u_{i}u_{i}\rangle$
and
$q^{2}=\langle u_{i}u_{i}\rangle$
and
![]() $\unicode[STIX]{x1D700}=\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{i}\rangle$
.
$\unicode[STIX]{x1D700}=\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{i}\rangle$
.
We mentioned in the introduction that the largest scales in the SSHST simulations are always constrained by their numerical box, and SDJ16 concluded that they are only useful as approximate models for other shear flows when
![]() $2<A_{xz}<5$
and
$2<A_{xz}<5$
and
![]() $A_{yz}>A_{xz}/2$
. These results are used to design the three simulations analysed in this paper, whose numerical parameters are summarised in table 1. They are labelled as L38, M32 and H32 by their ‘low’, ‘medium’ and ‘high’ Reynolds number (
$A_{yz}>A_{xz}/2$
. These results are used to design the three simulations analysed in this paper, whose numerical parameters are summarised in table 1. They are labelled as L38, M32 and H32 by their ‘low’, ‘medium’ and ‘high’ Reynolds number (
![]() $Re_{\unicode[STIX]{x1D706}}\approx$
50, 100 and 250), followed by their two aspect ratios. Basic flow statistics are compiled in table 2. We compare them with two channels in ‘large’ domains
$Re_{\unicode[STIX]{x1D706}}\approx$
50, 100 and 250), followed by their two aspect ratios. Basic flow statistics are compiled in table 2. We compare them with two channels in ‘large’ domains
![]() $(L_{x}=8\unicode[STIX]{x03C0}h,\,L_{z}=3\unicode[STIX]{x03C0}h)$
, and
$(L_{x}=8\unicode[STIX]{x03C0}h,\,L_{z}=3\unicode[STIX]{x03C0}h)$
, and
![]() $Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}h/\unicode[STIX]{x1D708}=934$
(denoted by C950, del Álamo et al.
Reference del Álamo, Jiménez, Zandonade and Moser2004) and
$Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}h/\unicode[STIX]{x1D708}=934$
(denoted by C950, del Álamo et al.
Reference del Álamo, Jiménez, Zandonade and Moser2004) and
![]() $Re_{\unicode[STIX]{x1D70F}}=2003$
(C2000, Hoyas & Jiménez Reference Hoyas and Jiménez2006). Although not discussed in detail in this paper, other HST simulations from SDJ16 are occasionally used to clarify the effect of the computational box on the statistics. They are labelled in the obvious way as L32, M34, etc.
$Re_{\unicode[STIX]{x1D70F}}=2003$
(C2000, Hoyas & Jiménez Reference Hoyas and Jiménez2006). Although not discussed in detail in this paper, other HST simulations from SDJ16 are occasionally used to clarify the effect of the computational box on the statistics. They are labelled in the obvious way as L32, M34, etc.

Figure 1. (a) Premultiplied one-dimensional spectra of the vorticity magnitude, normalised with the total enstrophy, as a function of the streamwise wavelength
![]() $\unicode[STIX]{x1D706}_{x}=2\unicode[STIX]{x03C0}/k_{x}$
, in Kolmogorov scaling. The vertical line is
$\unicode[STIX]{x1D706}_{x}=2\unicode[STIX]{x03C0}/k_{x}$
, in Kolmogorov scaling. The vertical line is
![]() $\unicode[STIX]{x1D706}_{x}/\unicode[STIX]{x1D702}=40$
. (b) One-dimensional co-spectra of
$\unicode[STIX]{x1D706}_{x}/\unicode[STIX]{x1D702}=40$
. (b) One-dimensional co-spectra of
![]() $u$
and
$u$
and
![]() $v$
normalised with
$v$
normalised with
![]() $u_{\unicode[STIX]{x1D70F}}$
and with the Corrsin length. The vertical line is
$u_{\unicode[STIX]{x1D70F}}$
and with the Corrsin length. The vertical line is
![]() $\unicode[STIX]{x1D706}_{x}/L_{c}=15$
. The solid lines are HST and the dashed ones are channels at
$\unicode[STIX]{x1D706}_{x}/L_{c}=15$
. The solid lines are HST and the dashed ones are channels at
![]() $y/h\approx 0.15$
, with symbols as in table 1.
$y/h\approx 0.15$
, with symbols as in table 1.
Table 2. Flow parameters for the three DNS of HST. Here,
![]() $\unicode[STIX]{x1D706}$
,
$\unicode[STIX]{x1D706}$
,
![]() $L_{\unicode[STIX]{x1D700}}$
and
$L_{\unicode[STIX]{x1D700}}$
and
![]() $S^{\ast }$
are respectively the Taylor and integral length scales, and the Corrsin (Reference Corrsin1958) shear parameter defined in the text.
$S^{\ast }$
are respectively the Taylor and integral length scales, and the Corrsin (Reference Corrsin1958) shear parameter defined in the text.

In the logarithmic layer of channels,
![]() $Re_{\unicode[STIX]{x1D706}}\approx 7{y^{+}}^{1/2}$
(Jiménez Reference Jiménez2013b
), so that the Reynolds number of L38 is similar to that in the buffer layer,
$Re_{\unicode[STIX]{x1D706}}\approx 7{y^{+}}^{1/2}$
(Jiménez Reference Jiménez2013b
), so that the Reynolds number of L38 is similar to that in the buffer layer,
![]() $y^{+}\approx 50$
, while those of M32 and H32 are equivalent to
$y^{+}\approx 50$
, while those of M32 and H32 are equivalent to
![]() $y^{+}\approx 200$
and
$y^{+}\approx 200$
and
![]() $y^{+}\approx 1300$
respectively. This comparison allows us to estimate the effective range of scales in our simulations, and how close they are to fully developed turbulence. Although the integral scale
$y^{+}\approx 1300$
respectively. This comparison allows us to estimate the effective range of scales in our simulations, and how close they are to fully developed turbulence. Although the integral scale
![]() $L_{\unicode[STIX]{x1D700}}=q^{3}/3\sqrt{3}\unicode[STIX]{x1D700}$
is usually taken to represent the largest flow scales, it was argued by Corrsin (Reference Corrsin1958) that a more relevant measure in shear flows is
$L_{\unicode[STIX]{x1D700}}=q^{3}/3\sqrt{3}\unicode[STIX]{x1D700}$
is usually taken to represent the largest flow scales, it was argued by Corrsin (Reference Corrsin1958) that a more relevant measure in shear flows is
![]() $L_{c}=(\unicode[STIX]{x1D700}/S^{3})^{1/2}$
, below which eddies are isotropically oriented and decouple from the effect of the mean shear. In this sense,
$L_{c}=(\unicode[STIX]{x1D700}/S^{3})^{1/2}$
, below which eddies are isotropically oriented and decouple from the effect of the mean shear. In this sense,
![]() $L_{c}$
is a measure of the small-scale limit of the energy-injection range, in the same way that the Kolmogorov scale
$L_{c}$
is a measure of the small-scale limit of the energy-injection range, in the same way that the Kolmogorov scale
![]() $\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D700})^{1/4}$
characterises the beginning of the dissipative range. It follows from their definition that
$\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D700})^{1/4}$
characterises the beginning of the dissipative range. It follows from their definition that
![]() $L_{c}=L_{\unicode[STIX]{x1D700}}(3/S^{\ast })^{3/2}$
. Since
$L_{c}=L_{\unicode[STIX]{x1D700}}(3/S^{\ast })^{3/2}$
. Since
![]() $S^{\ast }\approx 7{-}9$
both in HST (SDJ16) and in the logarithmic layer of wall-bounded flows (Jiménez Reference Jiménez2013b
), it follows that
$S^{\ast }\approx 7{-}9$
both in HST (SDJ16) and in the logarithmic layer of wall-bounded flows (Jiménez Reference Jiménez2013b
), it follows that
![]() $L_{c}\approx 0.25L_{\unicode[STIX]{x1D700}}$
. In our HSTs,
$L_{c}\approx 0.25L_{\unicode[STIX]{x1D700}}$
. In our HSTs,
![]() $L_{c}\approx 0.1L_{z}$
and
$L_{c}\approx 0.1L_{z}$
and
![]() $L_{c}/\unicode[STIX]{x1D702}\approx 0.033Re_{\unicode[STIX]{x1D706}}^{3/2}$
(see table 2). In the logarithmic layer of channels,
$L_{c}/\unicode[STIX]{x1D702}\approx 0.033Re_{\unicode[STIX]{x1D706}}^{3/2}$
(see table 2). In the logarithmic layer of channels,
![]() $L_{c}\approx 0.3y$
and
$L_{c}\approx 0.3y$
and
![]() $L_{c}/\unicode[STIX]{x1D702}\approx 0.4{y^{+}}^{3/4}$
.
$L_{c}/\unicode[STIX]{x1D702}\approx 0.4{y^{+}}^{3/4}$
.
Both
![]() $L_{c}$
and
$L_{c}$
and
![]() $\unicode[STIX]{x1D702}$
are characteristics scales, rather than absolute limits. Figure 1(a) shows enstrophy spectra in Kolmogorov scaling for the three HST cases and for the two channels, and figure 1(b) shows co-spectra of the tangential Reynolds stress scaled with the Corrsin length. Both collapse well, although the constricting effect of the numerical box on the Reynolds stress of the HST cases is obvious. It follows from these spectra that a reasonable lower limit of the inertial range is approximately
$\unicode[STIX]{x1D702}$
are characteristics scales, rather than absolute limits. Figure 1(a) shows enstrophy spectra in Kolmogorov scaling for the three HST cases and for the two channels, and figure 1(b) shows co-spectra of the tangential Reynolds stress scaled with the Corrsin length. Both collapse well, although the constricting effect of the numerical box on the Reynolds stress of the HST cases is obvious. It follows from these spectra that a reasonable lower limit of the inertial range is approximately
![]() $\ell _{\unicode[STIX]{x1D700}}\approx 40\unicode[STIX]{x1D702}$
. The largest active flow scale, in the sense of carrying Reynolds stress and net kinetic-energy production, is
$\ell _{\unicode[STIX]{x1D700}}\approx 40\unicode[STIX]{x1D702}$
. The largest active flow scale, in the sense of carrying Reynolds stress and net kinetic-energy production, is
![]() $L_{0}\approx 15L_{c}$
, so that the effective ‘inertial’ range of scales is approximately
$L_{0}\approx 15L_{c}$
, so that the effective ‘inertial’ range of scales is approximately
![]() $L_{0}/\ell _{\unicode[STIX]{x1D700}}=0.4L_{c}/\unicode[STIX]{x1D702}$
. Using the values in table 1,
$L_{0}/\ell _{\unicode[STIX]{x1D700}}=0.4L_{c}/\unicode[STIX]{x1D702}$
. Using the values in table 1,
![]() $L_{0}/\ell _{\unicode[STIX]{x1D700}}\approx 5$
, 14 and 50 for L38, M32 and H32 respectively, suggesting that the Reynolds number of L38 is probably too low to be considered as fully turbulent, and to be compared with the other two simulations.
$L_{0}/\ell _{\unicode[STIX]{x1D700}}\approx 5$
, 14 and 50 for L38, M32 and H32 respectively, suggesting that the Reynolds number of L38 is probably too low to be considered as fully turbulent, and to be compared with the other two simulations.
Due to the strong intermittency of HST (Pumir Reference Pumir1996), the instantaneous
![]() $\overline{\unicode[STIX]{x1D702}}(t)$
undergoes strong fluctuations. This is shown in table 1 by the standard deviation of the numerical resolution, which has to be set fine enough to capture well the smallest scales over the whole history. Our grids are adjusted to uniformly satisfy
$\overline{\unicode[STIX]{x1D702}}(t)$
undergoes strong fluctuations. This is shown in table 1 by the standard deviation of the numerical resolution, which has to be set fine enough to capture well the smallest scales over the whole history. Our grids are adjusted to uniformly satisfy
![]() $\unicode[STIX]{x1D6E5}/\overline{\unicode[STIX]{x1D702}}(t)\lesssim 1.5$
, which is the usual requirement for the study of vortex filaments in isotropic turbulence (Jiménez et al.
Reference Jiménez, Wray, Saffman and Rogallo1993). The result is that the simulation is over-resolved over much of its history, but it is also probably true that the resolution is marginal from the point of view of vorticity dynamics at isolated points during the most intense bursts. This is likely to be a local problem in most high-Reynolds-number simulations of turbulence, but it is made more obvious in minimal boxes because large-scale intermittency affects the whole flow at the same time.
$\unicode[STIX]{x1D6E5}/\overline{\unicode[STIX]{x1D702}}(t)\lesssim 1.5$
, which is the usual requirement for the study of vortex filaments in isotropic turbulence (Jiménez et al.
Reference Jiménez, Wray, Saffman and Rogallo1993). The result is that the simulation is over-resolved over much of its history, but it is also probably true that the resolution is marginal from the point of view of vorticity dynamics at isolated points during the most intense bursts. This is likely to be a local problem in most high-Reynolds-number simulations of turbulence, but it is made more obvious in minimal boxes because large-scale intermittency affects the whole flow at the same time.
3 Structure identification
The three-dimensional structure identification method used in this paper was first introduced for strong vorticity and strain rate in isotropic turbulence by Moisy & Jiménez (Reference Moisy and Jiménez2004), and extended by AJZM06 and LFJ12 to vortex clusters and Qs in channels. Defining the point-wise Reynolds stress as
![]() $\unicode[STIX]{x1D70F}=-uv$
, the Qs are defined as connected regions in which all of the points satisfy the intensity criterion
$\unicode[STIX]{x1D70F}=-uv$
, the Qs are defined as connected regions in which all of the points satisfy the intensity criterion
Vortex clusters are similarly defined as connected regions where the second invariant
![]() $\unicode[STIX]{x1D6F1}$
of the velocity-gradient tensor (Chong, Perry & Cantwell Reference Chong, Perry and Cantwell1990) exceeds a fraction
$\unicode[STIX]{x1D6F1}$
of the velocity-gradient tensor (Chong, Perry & Cantwell Reference Chong, Perry and Cantwell1990) exceeds a fraction
![]() $\unicode[STIX]{x1D6FC}$
of its r.m.s. value,
$\unicode[STIX]{x1D6FC}$
of its r.m.s. value,
It should be noted that
![]() $\unicode[STIX]{x1D6F1}^{\prime }$
,
$\unicode[STIX]{x1D6F1}^{\prime }$
,
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $v^{\prime }$
are functions of
$v^{\prime }$
are functions of
![]() $y$
in channels, but not in HST. It should be noted also that
$y$
in channels, but not in HST. It should be noted also that
![]() $\unicode[STIX]{x1D6F1}$
is often denoted by
$\unicode[STIX]{x1D6F1}$
is often denoted by
![]() $Q$
in publications, but we avoid that notation here to prevent confusion with the Q structures. The reason for choosing
$Q$
in publications, but we avoid that notation here to prevent confusion with the Q structures. The reason for choosing
![]() $\unicode[STIX]{x1D6F1}$
to define vortex clusters instead of the discriminant
$\unicode[STIX]{x1D6F1}$
to define vortex clusters instead of the discriminant
![]() $D$
(AJZM06; LFJ12) is the different numerical resolution requirements of the two quantities. The discriminant is a sixth power of the velocity derivatives, while
$D$
(AJZM06; LFJ12) is the different numerical resolution requirements of the two quantities. The discriminant is a sixth power of the velocity derivatives, while
![]() $\unicode[STIX]{x1D6F1}$
is only quadratic, and it was shown by Lozano-Durán, Holzner & Jiménez (Reference Lozano-Durán, Holzner and Jiménez2015) that high-order quantities can quickly become numerically meaningless when the resolution is marginal. Chakraborty, Balachandar & Adrian (Reference Chakraborty, Balachandar and Adrian2005) showed that there are few statistically significant differences between the various vortex identification methods.
$\unicode[STIX]{x1D6F1}$
is only quadratic, and it was shown by Lozano-Durán, Holzner & Jiménez (Reference Lozano-Durán, Holzner and Jiménez2015) that high-order quantities can quickly become numerically meaningless when the resolution is marginal. Chakraborty, Balachandar & Adrian (Reference Chakraborty, Balachandar and Adrian2005) showed that there are few statistically significant differences between the various vortex identification methods.
The thresholds
![]() $H$
and
$H$
and
![]() $\unicode[STIX]{x1D6FC}$
are determined by a percolation analysis similar to that in Moisy & Jiménez (Reference Moisy and Jiménez2004), AJZM06 and LFJ12. Briefly, the ratio
$\unicode[STIX]{x1D6FC}$
are determined by a percolation analysis similar to that in Moisy & Jiménez (Reference Moisy and Jiménez2004), AJZM06 and LFJ12. Briefly, the ratio
![]() $V_{lar}/V_{tot}$
between the volume of the largest connected structure and the total volume contained in all of the structures is computed as a function of the threshold. For a sufficiently low threshold, the volume fraction of the largest structure increases sharply, and would reach unity for structures of a single kind if the threshold were chosen low enough. The nominal threshold for identifying structures is chosen near the middle of the percolation transition.
$V_{lar}/V_{tot}$
between the volume of the largest connected structure and the total volume contained in all of the structures is computed as a function of the threshold. For a sufficiently low threshold, the volume fraction of the largest structure increases sharply, and would reach unity for structures of a single kind if the threshold were chosen low enough. The nominal threshold for identifying structures is chosen near the middle of the percolation transition.

Figure 2. Percolation diagram of the volume fraction of the largest structure
![]() $V_{lar}/V_{tot}$
as a fraction of the total volume of all identified structures. All curves are normalised with their maximum. (a) Qs. (b) Vortex clusters. The vertical dashed lines indicate the nominal thresholds,
$V_{lar}/V_{tot}$
as a fraction of the total volume of all identified structures. All curves are normalised with their maximum. (a) Qs. (b) Vortex clusters. The vertical dashed lines indicate the nominal thresholds,
![]() $H=(-uv)_{thr}/u^{\prime }v^{\prime }=1.75$
for Qs and
$H=(-uv)_{thr}/u^{\prime }v^{\prime }=1.75$
for Qs and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6F1}_{thr}/\unicode[STIX]{x1D6F1}^{\prime }=1.5$
for vortex clusters. Symbols are as in table 1. (c) Time history of the kinetic energy
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6F1}_{thr}/\unicode[STIX]{x1D6F1}^{\prime }=1.5$
for vortex clusters. Symbols are as in table 1. (c) Time history of the kinetic energy
![]() $\overline{q^{2}}(t)/\langle q^{2}\rangle$
of M32, divided into ——, energetic part
$\overline{q^{2}}(t)/\langle q^{2}\rangle$
of M32, divided into ——, energetic part
![]() $(\overline{q^{2}}(t)>\langle q^{2}\rangle )$
; – – –, quiescent part
$(\overline{q^{2}}(t)>\langle q^{2}\rangle )$
; – – –, quiescent part
![]() $(\overline{q^{2}}(t)<\langle q^{2}\rangle )$
. (d) Percolation diagram for vortex clusters in ◃, energetic
$(\overline{q^{2}}(t)<\langle q^{2}\rangle )$
. (d) Percolation diagram for vortex clusters in ◃, energetic
![]() $(h)$
; ▹, quiescent
$(h)$
; ▹, quiescent
![]() $(l)$
parts in (c). In each case, the threshold is defined with respect to the corresponding r.m.s.,
$(l)$
parts in (c). In each case, the threshold is defined with respect to the corresponding r.m.s.,
![]() $\unicode[STIX]{x1D6F1}_{h}^{\prime }$
or
$\unicode[STIX]{x1D6F1}_{h}^{\prime }$
or
![]() $\unicode[STIX]{x1D6F1}_{l}^{\prime }$
. The line without symbols is the global average of M32, from (b).
$\unicode[STIX]{x1D6F1}_{l}^{\prime }$
. The line without symbols is the global average of M32, from (b).
The resulting percolation diagrams are shown in figures 2(a) and 2(b), where
![]() $V_{lar}/V_{tot}$
is given as a function of the threshold, with each curve normalised by its maximum. The definition of individual structures becomes more computationally expensive for the lower thresholds because structures are larger, and it sometimes becomes impractical to perform the percolation analysis over the whole computational box. For example, the analysis of the vortex clusters of H32 for
$V_{lar}/V_{tot}$
is given as a function of the threshold, with each curve normalised by its maximum. The definition of individual structures becomes more computationally expensive for the lower thresholds because structures are larger, and it sometimes becomes impractical to perform the percolation analysis over the whole computational box. For example, the analysis of the vortex clusters of H32 for
![]() $\unicode[STIX]{x1D6FC}<0.25$
could only be done in our servers for a quarter of the computational box (AJZM06), but we tested that this restriction did not make any difference for the higher thresholds within the percolation transition. At very high thresholds, there is (generically) a single point in the thresholded set, forming a single structure. The consequent growth of
$\unicode[STIX]{x1D6FC}<0.25$
could only be done in our servers for a quarter of the computational box (AJZM06), but we tested that this restriction did not make any difference for the higher thresholds within the percolation transition. At very high thresholds, there is (generically) a single point in the thresholded set, forming a single structure. The consequent growth of
![]() $V_{lar}/V_{tot}$
towards unity is clearly seen in figure 2.
$V_{lar}/V_{tot}$
towards unity is clearly seen in figure 2.
There is a subtle difference between the processing of Qs here and in previous papers. In LFJ12, all the points satisfying (3.1) were first isolated and separated into individual structures, and each structure
![]() $\unicode[STIX]{x1D6FA}$
was then classified into a quadrant according to the mean values of its two velocity components, defined, for example, as
$\unicode[STIX]{x1D6FA}$
was then classified into a quadrant according to the mean values of its two velocity components, defined, for example, as
 $$\begin{eqnarray}u_{m}=\frac{\displaystyle \int _{\unicode[STIX]{x1D6FA}}u\,\text{d}V}{\displaystyle \int _{\unicode[STIX]{x1D6FA}}\,\text{d}V}.\end{eqnarray}$$
$$\begin{eqnarray}u_{m}=\frac{\displaystyle \int _{\unicode[STIX]{x1D6FA}}u\,\text{d}V}{\displaystyle \int _{\unicode[STIX]{x1D6FA}}\,\text{d}V}.\end{eqnarray}$$
For perfectly resolved simulations, finding points of different quadrants within a single contiguous structure would imply a discontinuity in the flow (since the sign of some velocity component would have to change discontinuously, LFJ12), and it was explicitly tested in LFJ12 that the number of structures with ‘mixed’ points was negligible. However, when the resolution is limited, it is possible for different quadrants to coexist within a structure defined in this way. Even in LFJ12, approximately 5 % of the total volume of the largest Qs belongs to quadrants that are different from the average quadrant of their structure.
To avoid ambiguities, the present paper classifies points individually into quadrants before clustering them into contiguous structures. This could not be done in channels, where the points within a given Q change quadrant when they cross the central plane, but it has the added advantage of requiring less computational resources, since the structures of each quadrant involve fewer points than the total. For example, the classification of Qs in H32 could not be performed in our home servers when treating all the Qs together during strong bursts.
The differences from the older method were tested in HST by comparing the results of the two schemes. The difference in the number of Qs identified by the two methods was approximately 4 % in L38 and less than 1 % in M32, but the volume of the largest structure found when identifying all the quadrants together could be two times larger than when treating them separately. The effect in channels was tested in C950. The difference in the number of structures was relatively small, consistent with the percentage of misclassified points mentioned above, but the volume of the largest Qs found using the old method in some flow fields was found to be up to 50 % larger than when using the new one. In both HST and channels, statistical properties such as the fraction of Reynolds stress carried by the Qs and its distribution among Q classes differ little between the two methods.
An unwelcome consequence of computing the four Q classes independently is that their percolation behaviours are not exactly the same. To avoid using multiple thresholds and to facilitate the comparison with channels, figure 2 is computed using the sum of the volumes of the four Q classes, even if each of them is computed independently. Moreover, it is clear from figure 2(a) that the threshold found in LFJ12 for channels
![]() $(H=1.75)$
is within the percolation transition in HST, at least for the two highest Reynolds numbers. This is the value used here as the nominal threshold. The analyses presented below were repeated for the range
$(H=1.75)$
is within the percolation transition in HST, at least for the two highest Reynolds numbers. This is the value used here as the nominal threshold. The analyses presented below were repeated for the range
![]() $H=1.25{-}2.25$
with similar results, and we will only refer from now on to structures identified using the nominal threshold, unless stated otherwise.
$H=1.25{-}2.25$
with similar results, and we will only refer from now on to structures identified using the nominal threshold, unless stated otherwise.
Most of these problems do not apply to vortex clusters, which have no classes. Figure 2(b) suggests a percolation transition in the range
![]() $\unicode[STIX]{x1D6FC}=0.2{-}3$
. We chose
$\unicode[STIX]{x1D6FC}=0.2{-}3$
. We chose
![]() $\unicode[STIX]{x1D6FC}=1.5$
as our nominal threshold, and tested the range
$\unicode[STIX]{x1D6FC}=1.5$
as our nominal threshold, and tested the range
![]() $\unicode[STIX]{x1D6FC}=0.75{-}2.5$
. Although the variable used here to define vortex clusters is different from that used in AJZM06 and LFJ12 for channels, the results are compared below without recomputing the channels with
$\unicode[STIX]{x1D6FC}=0.75{-}2.5$
. Although the variable used here to define vortex clusters is different from that used in AJZM06 and LFJ12 for channels, the results are compared below without recomputing the channels with
![]() $\unicode[STIX]{x1D6F1}$
. Besides the already mentioned evidence in Chakraborty et al. (Reference Chakraborty, Balachandar and Adrian2005), we have tested that clusters based on the discriminant and on
$\unicode[STIX]{x1D6F1}$
. Besides the already mentioned evidence in Chakraborty et al. (Reference Chakraborty, Balachandar and Adrian2005), we have tested that clusters based on the discriminant and on
![]() $\unicode[STIX]{x1D6F1}$
are visually and statistically indistinguishable in our channels.
$\unicode[STIX]{x1D6F1}$
are visually and statistically indistinguishable in our channels.
A more serious problem has to do with the intermittency associated with the small computational boxes of HST. The reference
![]() $u^{\prime }$
,
$u^{\prime }$
,
![]() $v^{\prime }$
and
$v^{\prime }$
and
![]() $\unicode[STIX]{x1D6F1}^{\prime }$
in (3.1)–(3.2) are averaged over the whole flow history. In the larger boxes of the computational channels, the intermittency is spatial, and temporal and spatial averages are roughly equivalent. The intermittency in the minimal computational boxes of HST is temporal, and it is unclear whether a single threshold is adequate to isolate structures at different moments.
$\unicode[STIX]{x1D6F1}^{\prime }$
in (3.1)–(3.2) are averaged over the whole flow history. In the larger boxes of the computational channels, the intermittency is spatial, and temporal and spatial averages are roughly equivalent. The intermittency in the minimal computational boxes of HST is temporal, and it is unclear whether a single threshold is adequate to isolate structures at different moments.
Table 1 gives the ratios of the standard deviations of
![]() $[\overline{u^{2}}(t)]^{1/2}$
,
$[\overline{u^{2}}(t)]^{1/2}$
,
![]() $[\overline{v^{2}}(t)]^{1/2}$
and
$[\overline{v^{2}}(t)]^{1/2}$
and
![]() $[\overline{\unicode[STIX]{x1D6F1}^{2}}(t)]^{1/2}$
with respect to their long-time means. They are substantial and appear to increase with increasing
$[\overline{\unicode[STIX]{x1D6F1}^{2}}(t)]^{1/2}$
with respect to their long-time means. They are substantial and appear to increase with increasing
![]() $Re_{\unicode[STIX]{x1D706}}$
, although part of that increase is probably statistical. The case with the lowest Reynolds number (L38) also has a larger box that is not minimal in the vertical direction, chosen precisely to improve its statistics. The standard deviations for a smaller box at the same Reynolds number (
$Re_{\unicode[STIX]{x1D706}}$
, although part of that increase is probably statistical. The case with the lowest Reynolds number (L38) also has a larger box that is not minimal in the vertical direction, chosen precisely to improve its statistics. The standard deviations for a smaller box at the same Reynolds number (
![]() $A_{yz}=2$
, case L32 in SDJ16) are very similar to those of M32, and those in the large channels, which contain many structures, are less than one per cent of the means. Figure 2(c) displays an example of the temporal history of the kinetic energy in M32, classified into ‘energetic’ and ‘quiescent’ parts depending on whether the instantaneous
$A_{yz}=2$
, case L32 in SDJ16) are very similar to those of M32, and those in the large channels, which contain many structures, are less than one per cent of the means. Figure 2(c) displays an example of the temporal history of the kinetic energy in M32, classified into ‘energetic’ and ‘quiescent’ parts depending on whether the instantaneous
![]() $\overline{q^{2}}(t)$
is respectively higher or lower than the overall average
$\overline{q^{2}}(t)$
is respectively higher or lower than the overall average
![]() $\langle q^{2}\rangle$
. In order to verify whether the percolation results in figure 2(b) depend on the state of the flow, we plot in figure 2(d) the percolation diagrams for vortex clusters in the quiescent and energetic flow periods. When a uniform threshold is used at all times, there are fewer structures in quiescent periods than in energetic ones, but figure 2(d) shows that, when the percolation is plotted with respect to a rescaled threshold,
$\langle q^{2}\rangle$
. In order to verify whether the percolation results in figure 2(b) depend on the state of the flow, we plot in figure 2(d) the percolation diagrams for vortex clusters in the quiescent and energetic flow periods. When a uniform threshold is used at all times, there are fewer structures in quiescent periods than in energetic ones, but figure 2(d) shows that, when the percolation is plotted with respect to a rescaled threshold,
![]() $\unicode[STIX]{x1D6F1}_{thr}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6F1}_{j}^{\prime }$
, where
$\unicode[STIX]{x1D6F1}_{thr}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6F1}_{j}^{\prime }$
, where
![]() $\unicode[STIX]{x1D6F1}_{j}^{\prime }$
is
$\unicode[STIX]{x1D6F1}_{j}^{\prime }$
is
![]() $j=h$
or
$j=h$
or
![]() $j=l$
according to whether the statistics are compiled over the energetic or quiescent periods, the percolation diagrams collapse well, even if
$j=l$
according to whether the statistics are compiled over the energetic or quiescent periods, the percolation diagrams collapse well, even if
![]() $\unicode[STIX]{x1D6F1}_{h}^{\prime }/\unicode[STIX]{x1D6F1}_{l}^{\prime }=1.7$
. This strongly suggests that the physics of the structures differs little between the two periods, and that most of the differences in their identification could be accounted for by a temporally variable threshold. However, doing so would complicate the comparison with the spatially intermittent channels, and we use a constant threshold for all times.
$\unicode[STIX]{x1D6F1}_{h}^{\prime }/\unicode[STIX]{x1D6F1}_{l}^{\prime }=1.7$
. This strongly suggests that the physics of the structures differs little between the two periods, and that most of the differences in their identification could be accounted for by a temporally variable threshold. However, doing so would complicate the comparison with the spatially intermittent channels, and we use a constant threshold for all times.
Table 3. Parameters of the structures used in the paper. Here,
![]() $ST$
is the total simulation time measured in terms of the shear;
$ST$
is the total simulation time measured in terms of the shear;
![]() $T_{eto}\approx 0.4ST$
is the time in terms of the eddy turnover defined as
$T_{eto}\approx 0.4ST$
is the time in terms of the eddy turnover defined as
![]() $L_{\unicode[STIX]{x1D700}}/\sqrt{q^{2}/3}$
;
$L_{\unicode[STIX]{x1D700}}/\sqrt{q^{2}/3}$
;
![]() $N_{F}$
is the number of flow fields used to extract the structures;
$N_{F}$
is the number of flow fields used to extract the structures;
![]() $N_{C}$
and
$N_{C}$
and
![]() $N_{Q}$
are the numbers of vortex clusters and Qs identified with
$N_{Q}$
are the numbers of vortex clusters and Qs identified with
![]() $\unicode[STIX]{x1D6FC}$
=1.5 and
$\unicode[STIX]{x1D6FC}$
=1.5 and
![]() $H$
=1.75 respectively. For these thresholds,
$H$
=1.75 respectively. For these thresholds,
![]() $N_{i}$
and
$N_{i}$
and
![]() $V_{i}$
are the percentages of Q of each class in terms of their number and volume.
$V_{i}$
are the percentages of Q of each class in terms of their number and volume.

Table 3 contains information about the coherent structures identified, after structures with volume smaller than
![]() $(5\unicode[STIX]{x1D702})^{3}$
are discarded to avoid resolution issues. These small fragments typically represent a third of the total number of structures, but they only account for a negligible fraction of the total volume of the Qs, and for 1 %–2 % of the total volume of the vortex clusters.
$(5\unicode[STIX]{x1D702})^{3}$
are discarded to avoid resolution issues. These small fragments typically represent a third of the total number of structures, but they only account for a negligible fraction of the total volume of the Qs, and for 1 %–2 % of the total volume of the vortex clusters.
The Qs and vortex clusters account respectively for roughly 10 % and 3.5 % of the volume of the computational box at the reference threshold. Although the number of Qs is split roughly equally between the four quadrants at
![]() $H=1.75$
, their volume is mainly contributed by the Q
$H=1.75$
, their volume is mainly contributed by the Q
![]() $^{-}$
s, distributed equally in Q2s and Q4s, as expected from symmetry.
$^{-}$
s, distributed equally in Q2s and Q4s, as expected from symmetry.
We mentioned in the introduction that structures in channels can be classified as attached or detached according to whether their root reaches the neighbourhood of the wall or not, and that most of the volume and the Reynolds stresses of Qs are contained in the attached family (AJZM06; LFJ12). There are no walls in HST, but a related classification can be established between large and small structures. We have already seen that structures smaller than the Corrsin (Reference Corrsin1958) scale decouple from the shear. For example, vorticity becomes more isotropic as it moves away from the wall to scales smaller than
![]() $L_{c}$
(Jiménez Reference Jiménez2013b
). A rough classification of the structures in HST can thus be based on whether some characteristic size is larger or smaller than
$L_{c}$
(Jiménez Reference Jiménez2013b
). A rough classification of the structures in HST can thus be based on whether some characteristic size is larger or smaller than
![]() $L_{c}$
. Large and small structures can be expected a priori to be roughly equivalent to the attached and detached ones in channels. Whether this is actually the case will be examined below.
$L_{c}$
. Large and small structures can be expected a priori to be roughly equivalent to the attached and detached ones in channels. Whether this is actually the case will be examined below.

Figure 3. (a,b) Instantaneous structures extracted from the HST case M32 for (a) Q2 and (b) a vortex cluster, coloured by the vertical coordinate. (c,d) As in (a,b) for attached structures in the channel C2000, coloured by the distance from the wall. In all cases, structures are defined by the nominal threshold explained in the respective papers.
The probability density function (p.d.f.) of the volume of the Qs is roughly proportional to
![]() $V^{-5/3}$
at these Reynolds numbers. As a consequence, most Qs are small, but most of their volume is contained in large structures. For example, Qs with
$V^{-5/3}$
at these Reynolds numbers. As a consequence, most Qs are small, but most of their volume is contained in large structures. For example, Qs with
![]() $V>L_{c}^{3}$
contribute roughly 20 % of the number of structures in L38, and an almost negligible fraction in H32, but they account for 96.5 % and 87.6 % of the total volume respectively. In channels, approximately 70 % of the total Q volume is in tall attached Qs at all Reynolds numbers (LFJ12).
$V>L_{c}^{3}$
contribute roughly 20 % of the number of structures in L38, and an almost negligible fraction in H32, but they account for 96.5 % and 87.6 % of the total volume respectively. In channels, approximately 70 % of the total Q volume is in tall attached Qs at all Reynolds numbers (LFJ12).
The p.d.f. of the volume of the vortex clusters is steeper,
![]() $V^{-4}$
, so that small eddies dominate both in number and in volume. Large
$V^{-4}$
, so that small eddies dominate both in number and in volume. Large
![]() $(V>L_{c}^{3})$
vortex clusters account for 8.6 % of the total number of vortex clusters in L38, and for a negligible fraction in the two higher-Reynolds-number cases. Their contribution to the total volume also becomes less important as the Reynolds number increases (61.7 %, 3.0 % and 0.5 % for the three HST cases). Attached vortex clusters only occupy 10 %–15 % of the total cluster volume in channels, although their association with attached Q2s (AJZM06; LFJ12) has made them the subject of intensive study as markers of the momentum and energy cascades across different scales.
$(V>L_{c}^{3})$
vortex clusters account for 8.6 % of the total number of vortex clusters in L38, and for a negligible fraction in the two higher-Reynolds-number cases. Their contribution to the total volume also becomes less important as the Reynolds number increases (61.7 %, 3.0 % and 0.5 % for the three HST cases). Attached vortex clusters only occupy 10 %–15 % of the total cluster volume in channels, although their association with attached Q2s (AJZM06; LFJ12) has made them the subject of intensive study as markers of the momentum and energy cascades across different scales.
It will be found convenient in the rest to the paper to characterise the size of eddies by the ‘box diagonal’,
![]() $d$
, of a circumscribing parallelepiped aligned to the three coordinate directions (see figure 3). The relation between
$d$
, of a circumscribing parallelepiped aligned to the three coordinate directions (see figure 3). The relation between
![]() $d$
and the volume of the structure will be discussed in § 4.3. It depends on the type of structure and weakly on the Reynolds number, but
$d$
and the volume of the structure will be discussed in § 4.3. It depends on the type of structure and weakly on the Reynolds number, but
![]() $V=L_{c}^{3}$
corresponds to
$V=L_{c}^{3}$
corresponds to
![]() $d/L_{c}\approx 4$
for Qs, and
$d/L_{c}\approx 4$
for Qs, and
![]() $d/L_{c}\approx 7$
for vortex clusters in M32.
$d/L_{c}\approx 7$
for vortex clusters in M32.
Examples of an instantaneous Q2 and of a vortex cluster from the HST case M32 are shown in figure 3(a,b). They can be compared with the equivalent figures of structures in channels in figure 3(c,d), as well as with AJZM06 and LFJ12, or with the larger online collection of channel structures in http://turbulent beautycontest.appspot.com/. Although visual impressions should not substitute statistical analysis, the comparison reinforces the idea that the structures in HST are very similar to those in channels, especially to those detached from the wall.
4 Properties of the structures in HST and in channels
One of the motivations of this paper is to explore how coherent structures in HST are related to those in channels. Both flows draw their energy from the mean shear, but the channel is inhomogeneous in
![]() $y$
and has walls, while HST is homogeneous and has no walls. It is then reasonable to infer that properties shared by the structures in both flows are primarily due to the local shear, while those that are different are related either to inhomogeneity or to the presence of the wall. In this section, we study the geometrical and flow properties of the structures defined above, and enquire about their similarities and differences with the rest of the flow, and with the channel.
$y$
and has walls, while HST is homogeneous and has no walls. It is then reasonable to infer that properties shared by the structures in both flows are primarily due to the local shear, while those that are different are related either to inhomogeneity or to the presence of the wall. In this section, we study the geometrical and flow properties of the structures defined above, and enquire about their similarities and differences with the rest of the flow, and with the channel.
Before doing so, it is important to understand some differences between the two flows, even when considering channels far from walls. The first one concerns symmetry. If we denote a transformation by its effect on the flow variables, both channels and HST are statistically symmetric with respect to reflections across vertical
![]() $(x,y)$
planes, written as
$(x,y)$
planes, written as
This symmetry was used in LFJ12 to simplify some statistics, and will be used here for the same purpose. A symmetry of HST that is not shared by the channel is reflection across horizontal
![]() $(x,z)$
planes, which changes the sign of
$(x,z)$
planes, which changes the sign of
![]() $u$
and
$u$
and
![]() $v$
,
$v$
,
The product of these two symmetries is an inversion with respect to the origin, also exclusive to HST,
These symmetries can be used to constrain which relations among structures are statistically possible. For example, it was found in AJZM06 and LFJ12 that vortex clusters in channels tend to be associated with Q2s rather than with Q4s, but S3 leaves invariant the definition of vortex clusters, and transforms Q2s into Q4s. This implies that any preference of vortex clusters for Q2s or Q4s is statistically impossible in HST, and has to be a consequence of the differential advection of vorticity towards and away from the wall (Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014). It was also found in LFJ12 that the volume occupied by Q2s in channels is larger than that of the Q4s, especially for the largest structures, but the previous argument shows that the two should be similar in HST (as well as those of Q1s and Q3s). This is confirmed by the simulations, and statistics for HST will mostly be given in terms of Q
![]() $^{+}$
s and Q
$^{+}$
s and Q
![]() $^{-}$
s from now on.
$^{-}$
s from now on.
Another important difference between channels and our HST simulations is that the largest scales in the latter are limited in the spanwise direction by the computational box (SDJ16), while the flow in large channels is only constrained vertically by the wall. The consequence is that only relatively small scales (empirically smaller than
![]() $d\approx L_{z}/2\approx 5L_{c}$
) should be expected to behave similarly in the two cases.
$d\approx L_{z}/2\approx 5L_{c}$
) should be expected to behave similarly in the two cases.
4.1 Reynolds stress
The fraction of the total Reynolds stress carried by Qs in HST is listed in the first column of table 4. The next two columns give the distribution into Q classes, which roughly agrees with Pumir (Reference Pumir1996). At least within our range of Reynolds numbers, there is a weak trend towards a smaller overall fraction of Reynolds stress being carried by intense Qs as the Reynolds number increases, due both to stronger counter-gradient Q
![]() $^{+}$
s and to weaker co-gradient Q
$^{+}$
s and to weaker co-gradient Q
![]() $^{-}$
s. Since the fluctuation intensities reflect the sum of Q
$^{-}$
s. Since the fluctuation intensities reflect the sum of Q
![]() $^{+}$
s and Q
$^{+}$
s and Q
![]() $^{-}$
s, while the Reynolds stress reflects their difference, a consequence is that the correlation coefficient
$^{-}$
s, while the Reynolds stress reflects their difference, a consequence is that the correlation coefficient
![]() $c_{uv}=-\langle uv\rangle /u^{\prime }v^{\prime }$
between
$c_{uv}=-\langle uv\rangle /u^{\prime }v^{\prime }$
between
![]() $u$
and
$u$
and
![]() $v$
decreases from roughly 0.41 in L38 to 0.37 in H32. A similar trend of
$v$
decreases from roughly 0.41 in L38 to 0.37 in H32. A similar trend of
![]() $c_{uv}$
is found in wall-bounded flows as the Reynolds number increases. In that case, it is usually attributed to the increased importance of the inactive motions due to the blocking effect of the wall (Townsend Reference Townsend1961), but the present results suggest that there is at least some contribution from an increased cancellation among stress-carrying eddies of different kinds. Table 4 includes data from the ‘logarithmic’ range of wall distances in channel C950. They are comparable to those in HST, including the amount of momentum backscatter (Q
$c_{uv}$
is found in wall-bounded flows as the Reynolds number increases. In that case, it is usually attributed to the increased importance of the inactive motions due to the blocking effect of the wall (Townsend Reference Townsend1961), but the present results suggest that there is at least some contribution from an increased cancellation among stress-carrying eddies of different kinds. Table 4 includes data from the ‘logarithmic’ range of wall distances in channel C950. They are comparable to those in HST, including the amount of momentum backscatter (Q
![]() $^{+}$
).
$^{+}$
).
Table 4. Fraction of the Reynolds stress and enstrophy contained in structures with the nominal threshold. The column Q is the percentage of the total Reynolds stress in Qs. The columns Q
![]() $^{\pm }$
refer to the stress in each Q class, while the subscript ‘
$^{\pm }$
refer to the stress in each Q class, while the subscript ‘
![]() $C$
’ refers to Qs whose box diagonal is
$C$
’ refers to Qs whose box diagonal is
![]() $d>L_{c}$
, where
$d>L_{c}$
, where
![]() $L_{c}$
is the Corrsin scale. The final column is the percentage of total enstrophy within vortex clusters. Data for the channel C950 in the range
$L_{c}$
is the Corrsin scale. The final column is the percentage of total enstrophy within vortex clusters. Data for the channel C950 in the range
![]() $y^{+}\geqslant 100$
and
$y^{+}\geqslant 100$
and
![]() $y/h<0.4$
are included for comparison (LFJ12). The ‘
$y/h<0.4$
are included for comparison (LFJ12). The ‘
![]() $C$
’ subscript refers in this case to attached Qs.
$C$
’ subscript refers in this case to attached Qs.

An important property of channels is that only large attached Q
![]() $^{-}$
s carry net Reynolds stress, and that there are basically no large attached Q
$^{-}$
s carry net Reynolds stress, and that there are basically no large attached Q
![]() $^{+}$
s (LFJ12). For smaller detached structures, the counter-gradient contribution of the Q
$^{+}$
s (LFJ12). For smaller detached structures, the counter-gradient contribution of the Q
![]() $^{+}$
s cancels the co-gradient contribution of the Q
$^{+}$
s cancels the co-gradient contribution of the Q
![]() $^{-}$
s. The simplest interpretation is that a net Reynolds stress can only be produced by eddies larger than the Corrsin (Reference Corrsin1958) scale, in which statistical isotropy is broken by coupling with the shear, and that those eddies are mostly co-gradient. Observations in channels cannot easily distinguish whether the asymmetry between Q
$^{-}$
s. The simplest interpretation is that a net Reynolds stress can only be produced by eddies larger than the Corrsin (Reference Corrsin1958) scale, in which statistical isotropy is broken by coupling with the shear, and that those eddies are mostly co-gradient. Observations in channels cannot easily distinguish whether the asymmetry between Q
![]() $^{+}$
and Q
$^{+}$
and Q
![]() $^{-}$
is due to the size of the eddies or to the presence of the wall.
$^{-}$
is due to the size of the eddies or to the presence of the wall.
This is tested for HST in the right-hand part of table 4, which lists the fraction of the total stress carried by ‘active’ Q
![]() $_{C}$
with
$_{C}$
with
![]() $d>L_{c}$
. Comparing with the left-most columns of the table, it is clear that large structures are also responsible for most of the momentum transfer in the absence of walls. In fact, it can be shown that there are very few Q
$d>L_{c}$
. Comparing with the left-most columns of the table, it is clear that large structures are also responsible for most of the momentum transfer in the absence of walls. In fact, it can be shown that there are very few Q
![]() $^{+}$
s larger than
$^{+}$
s larger than
![]() $d\approx 5L_{c}$
(see also figure 5
b below). Although not strictly equivalent, Pumir (Reference Pumir1996) mentions that 60 %–70 % of the Reynolds stress in a cubic HST box is carried by the first spanwise mode, whose wavelength is approximately
$d\approx 5L_{c}$
(see also figure 5
b below). Although not strictly equivalent, Pumir (Reference Pumir1996) mentions that 60 %–70 % of the Reynolds stress in a cubic HST box is carried by the first spanwise mode, whose wavelength is approximately
![]() $10L_{c}$
.
$10L_{c}$
.
The last column of table 4 shows that the fraction of enstrophy carried by vortex clusters increases slowly with the Reynolds number.
4.2 Flow anisotropy

Figure 4. (a) Shifted Lumley invariants of the Reynolds-stress anisotropy tensor: ▫, M32; ○, H32; ▵, channel C2000 above the buffer layer, with the symbol marking the lower limit,
![]() $y^{+}=100$
. Lines with closed symbols are unconditional statistics. Those with open symbols are conditioned to Q
$y^{+}=100$
. Lines with closed symbols are unconditional statistics. Those with open symbols are conditioned to Q
![]() $^{-}$
s. For the two HST cases, the identification threshold increases in the direction of the arrow from
$^{-}$
s. For the two HST cases, the identification threshold increases in the direction of the arrow from
![]() $H=0.25$
to 4. The channel is only drawn for
$H=0.25$
to 4. The channel is only drawn for
![]() $H=1.75$
. The inset is a zoom of the region around the nominal threshold
$H=1.75$
. The inset is a zoom of the region around the nominal threshold
![]() $H=1.75$
, marked by symbols. The thin dashed line at the top of the figure is the realisability limit for the invariants. The thicker dashed line that follows the thresholded HST cases is the result for a thresholded velocity field with joint-Gaussian statistics and a correlation coefficient
$H=1.75$
, marked by symbols. The thin dashed line at the top of the figure is the realisability limit for the invariants. The thicker dashed line that follows the thresholded HST cases is the result for a thresholded velocity field with joint-Gaussian statistics and a correlation coefficient
![]() $c_{uv}=-0.4$
. (b) The thin solid elliptical contours are the joint p.d.f.,
$c_{uv}=-0.4$
. (b) The thin solid elliptical contours are the joint p.d.f.,
![]() $p_{G}(u/u^{\prime },v/v^{\prime })$
, of two Gaussian variables with
$p_{G}(u/u^{\prime },v/v^{\prime })$
, of two Gaussian variables with
![]() $c_{uv}=-0.4$
. They contain 10 %, 50 % and 90 % of the points. The thicker solid ones are
$c_{uv}=-0.4$
. They contain 10 %, 50 % and 90 % of the points. The thicker solid ones are
![]() $-p_{G}uv/u^{\prime }v^{\prime }$
, with contours
$-p_{G}uv/u^{\prime }v^{\prime }$
, with contours
![]() $[0.2,0.5,0.8]$
of its maximum. The dashed ones are the same quantity for M32, and the chain-dotted ones are for C2000 at roughly the same Reynolds number
$[0.2,0.5,0.8]$
of its maximum. The dashed ones are the same quantity for M32, and the chain-dotted ones are for C2000 at roughly the same Reynolds number
![]() $(y/h=0.15)$
. The two hyperbolas are
$(y/h=0.15)$
. The two hyperbolas are
![]() $H=-1.75$
.
$H=-1.75$
.
Another question is whether the flow within Qs is different from the flow as a whole. Figure 4(a) displays the Lumley invariants, which are defined from the anisotropy tensor of the Reynolds stresses,
![]() $\unicode[STIX]{x1D623}_{ij}=\langle u_{i}u_{j}\rangle /\langle u_{i}u_{i}\rangle -\unicode[STIX]{x1D6FF}_{ij}/3$
, as
$\unicode[STIX]{x1D623}_{ij}=\langle u_{i}u_{j}\rangle /\langle u_{i}u_{i}\rangle -\unicode[STIX]{x1D6FF}_{ij}/3$
, as
![]() $\unicode[STIX]{x1D701}^{2}=\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{ji}/6$
and
$\unicode[STIX]{x1D701}^{2}=\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{ji}/6$
and
![]() $\unicode[STIX]{x1D709}^{3}=\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{jk}\unicode[STIX]{x1D623}_{ki}/6$
(Pope Reference Pope2000). The dashed curve at the top of the figure is the two-component realisability limit, and the right-hand vertical axis is the axisymmetric one. The point where the two lines meet in the upper-right part of the plot corresponds to one-component flows. Isotropic flow is at
$\unicode[STIX]{x1D709}^{3}=\unicode[STIX]{x1D623}_{ij}\unicode[STIX]{x1D623}_{jk}\unicode[STIX]{x1D623}_{ki}/6$
(Pope Reference Pope2000). The dashed curve at the top of the figure is the two-component realisability limit, and the right-hand vertical axis is the axisymmetric one. The point where the two lines meet in the upper-right part of the plot corresponds to one-component flows. Isotropic flow is at
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D701}=0$
, below the lower-right corner of the plot. The two solid symbols in the lower part of the plot correspond to unconditioned statistics of the HST cases M32 and H32, with the Reynolds number increasing towards the right. The line marked with the solid triangle is C2000 for
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D701}=0$
, below the lower-right corner of the plot. The two solid symbols in the lower part of the plot correspond to unconditioned statistics of the HST cases M32 and H32, with the Reynolds number increasing towards the right. The line marked with the solid triangle is C2000 for
![]() $y^{+}>100$
, moving towards isotropy as
$y^{+}>100$
, moving towards isotropy as
![]() $y$
increases towards the right. The kink in the line is
$y$
increases towards the right. The kink in the line is
![]() $y/h\approx 0.2$
, and the two points for HST are near the top of the logarithmic layer of the channel,
$y/h\approx 0.2$
, and the two points for HST are near the top of the logarithmic layer of the channel,
![]() $y/h\approx 0.3{-}0.4$
.
$y/h\approx 0.3{-}0.4$
.
The shorter lines in the upper-right part of the plot are conditioned to points within Q
![]() $^{-}$
s. The two roughly diagonal solid curves are the HST cases, with thresholds that increase from
$^{-}$
s. The two roughly diagonal solid curves are the HST cases, with thresholds that increase from
![]() $H=0.25$
to
$H=0.25$
to
![]() $H=4$
in the direction of the arrow. The kinked line marked with a triangle is the channel
$H=4$
in the direction of the arrow. The kinked line marked with a triangle is the channel
![]() $(H=1.75)$
, with the kink at
$(H=1.75)$
, with the kink at
![]() $y/h\approx 0.2$
and
$y/h\approx 0.2$
and
![]() $y$
increasing away from the triangle
$y$
increasing away from the triangle
![]() $(y^{+}=100)$
. The inset is an enlargement of this part of the plot. The symbols of the HST cases in the inset are for the nominal threshold
$(y^{+}=100)$
. The inset is an enlargement of this part of the plot. The symbols of the HST cases in the inset are for the nominal threshold
![]() $H=1.75$
, and show that the conditional statistics in HST also approximate those in the logarithmic layer of channels. It is clear from the figure that Q
$H=1.75$
, and show that the conditional statistics in HST also approximate those in the logarithmic layer of channels. It is clear from the figure that Q
![]() $^{-}$
s are more dominated by a single velocity component than the flow in general, and that this dominance is higher for the stronger events. Both within and outside the structures, the dominant velocity component is
$^{-}$
s are more dominated by a single velocity component than the flow in general, and that this dominance is higher for the stronger events. Both within and outside the structures, the dominant velocity component is
![]() $u$
. A similar figure can be drawn for C950.
$u$
. A similar figure can be drawn for C950.
However, we should be careful to distinguish between actual properties of the flow and artefacts created by the definition of the Qs. It was shown by Antonia & Atkinson (Reference Antonia and Atkinson1973) and Lu & Willmarth (Reference Lu and Willmarth1973) that the joint p.d.f. of
![]() $u$
and
$u$
and
![]() $v$
in a boundary layer is essentially that of two Gaussian variables with the correct cross-correlation coefficient,
$v$
in a boundary layer is essentially that of two Gaussian variables with the correct cross-correlation coefficient,
![]() $c_{uv}\approx -0.4$
. The thick dashed line in figure 4(a), largely hidden by the thresholded results, is the locus of the two Lumley invariants of such a joint-Gaussian distribution, thresholded in the same way as the Q
$c_{uv}\approx -0.4$
. The thick dashed line in figure 4(a), largely hidden by the thresholded results, is the locus of the two Lumley invariants of such a joint-Gaussian distribution, thresholded in the same way as the Q
![]() $^{-}$
s. It agrees very well with the simulation results.
$^{-}$
s. It agrees very well with the simulation results.
Figure 4(b) plots the joint p.d.f.,
![]() $p(u,v)$
, of two Gaussian variables, together with the
$p(u,v)$
, of two Gaussian variables, together with the
![]() $H=-1.75$
threshold for Q
$H=-1.75$
threshold for Q
![]() $^{-}$
s. It also includes the product
$^{-}$
s. It also includes the product
![]() $p(u,v)uv$
, whose integral is the Reynolds stress, plotted both for the joint-Gaussian distribution and for M32. They agree very well, suggesting that most statistical moments computed for these two velocity components using a joint-Gaussian distribution should agree well with the simulation results. The chain-dotted lines in the figure are for C2000. They also agree reasonably well with the HST and with the Gaussian model, although the asymmetry between Q2s and Q4s suggests that the latter are weaker because they come from the outer part of the channel, where the shear and the velocity fluctuations are weaker.
$p(u,v)uv$
, whose integral is the Reynolds stress, plotted both for the joint-Gaussian distribution and for M32. They agree very well, suggesting that most statistical moments computed for these two velocity components using a joint-Gaussian distribution should agree well with the simulation results. The chain-dotted lines in the figure are for C2000. They also agree reasonably well with the HST and with the Gaussian model, although the asymmetry between Q2s and Q4s suggests that the latter are weaker because they come from the outer part of the channel, where the shear and the velocity fluctuations are weaker.

Figure 5. (a) Anisotropy of the Reynolds-stress tensor within Qs, as a function of their box diagonal: ♢, L38; ▫, M32; ○, H32;
![]() $H=1.75$
. Open symbols are for Q
$H=1.75$
. Open symbols are for Q
![]() $_{uv}$
and closed ones are for Q
$_{uv}$
and closed ones are for Q
![]() $_{uw}$
. (b) Probability density function of the box diagonal of Qs defined from different variable pairs. Case M32 and
$_{uw}$
. (b) Probability density function of the box diagonal of Qs defined from different variable pairs. Case M32 and
![]() $H=1.75$
: ——, Q
$H=1.75$
: ——, Q
![]() $_{uv}$
; – – –, Q
$_{uv}$
; – – –, Q
![]() $_{uw}$
; – ⋅ – ⋅ –, Q
$_{uw}$
; – ⋅ – ⋅ –, Q
![]() $_{vw}$
; –▵–, Q
$_{vw}$
; –▵–, Q
![]() $_{uv}$
of C2000 centred at
$_{uv}$
of C2000 centred at
![]() $y/h\in (0.1,0.2)$
, where
$y/h\in (0.1,0.2)$
, where
![]() $Re_{\unicode[STIX]{x1D706}}\approx 100$
. In the case of Q
$Re_{\unicode[STIX]{x1D706}}\approx 100$
. In the case of Q
![]() $_{uv}$
, open symbols are Q
$_{uv}$
, open symbols are Q
![]() $^{+}$
and closed ones are Q
$^{+}$
and closed ones are Q
![]() $^{-}$
.
$^{-}$
.
Large and small structures are different from the point of view of the flow anisotropy. The open symbols in figure 5(a) show the mean second Lumley invariant of the flow within Qs, as a function of their size. This quantity is proportional to the Euclidean norm of
![]() $\unicode[STIX]{x1D623}_{ij}$
and is a measure of the anisotropy of the Reynolds-stress tensor. It ranges from
$\unicode[STIX]{x1D623}_{ij}$
and is a measure of the anisotropy of the Reynolds-stress tensor. It ranges from
![]() $\unicode[STIX]{x1D701}=0$
for full isotropy to
$\unicode[STIX]{x1D701}=0$
for full isotropy to
![]() $\unicode[STIX]{x1D701}=1/3$
for one-component flows. It is clear that the flow is roughly isotropic within structures with
$\unicode[STIX]{x1D701}=1/3$
for one-component flows. It is clear that the flow is roughly isotropic within structures with
![]() $d\lesssim L_{c}$
, which are decoupled from the shear, and only becomes anisotropic within large Qs.
$d\lesssim L_{c}$
, which are decoupled from the shear, and only becomes anisotropic within large Qs.
At this point, it may be useful to reflect on the meaning of defining Qs that are much smaller than
![]() $L_{c}$
. There is no problem in understanding small vortices, because enstrophy is a scalar quantity, independent of the orientation of the frame of reference. However, Qs are defined in terms of the product of two velocity components,
$L_{c}$
. There is no problem in understanding small vortices, because enstrophy is a scalar quantity, independent of the orientation of the frame of reference. However, Qs are defined in terms of the product of two velocity components,
![]() $u$
and
$u$
and
![]() $v$
, which can only be defined with reference to a given frame orientation. In a shear flow, the frame of reference is linked to the shear: the streamwise velocity
$v$
, which can only be defined with reference to a given frame orientation. In a shear flow, the frame of reference is linked to the shear: the streamwise velocity
![]() $u$
is the component along the direction of the mean flow, and
$u$
is the component along the direction of the mean flow, and
![]() $v$
is the component in the direction of the shear. Small structures that do not couple with the shear cannot have any statistically preferred direction, and there is no reason for either
$v$
is the component in the direction of the shear. Small structures that do not couple with the shear cannot have any statistically preferred direction, and there is no reason for either
![]() $u$
or
$u$
or
![]() $v$
to be especial. From the point of view of these structures, the mean flow appears as isotropic, and all of the velocity components are equivalent. It was indeed found in LFJ12 that the statistics of small Qs are indistinguishable among many different turbulent flows, including some without local shear, implying that many apparently meaningful statistics of small Qs are artefacts of their definition, and cannot be specific to a particular kind of eddy. For example, the closed symbols in figure 5(a) correspond to Q
$v$
to be especial. From the point of view of these structures, the mean flow appears as isotropic, and all of the velocity components are equivalent. It was indeed found in LFJ12 that the statistics of small Qs are indistinguishable among many different turbulent flows, including some without local shear, implying that many apparently meaningful statistics of small Qs are artefacts of their definition, and cannot be specific to a particular kind of eddy. For example, the closed symbols in figure 5(a) correspond to Q
![]() $_{uw}$
structures, which are defined from points in the flow for which
$_{uw}$
structures, which are defined from points in the flow for which
![]() $|uw|>Hu^{\prime }v^{\prime }$
(note that the threshold has been kept as in Q
$|uw|>Hu^{\prime }v^{\prime }$
(note that the threshold has been kept as in Q
![]() $_{uv}$
, for consistency). For small sizes, the anisotropy within these new structures is essentially the same as within the Q
$_{uv}$
, for consistency). For small sizes, the anisotropy within these new structures is essentially the same as within the Q
![]() $_{uv}$
. The two types of Qs only differ when they are large, in which case the Q
$_{uv}$
. The two types of Qs only differ when they are large, in which case the Q
![]() $_{uv}$
couple with the shear, but the Q
$_{uv}$
couple with the shear, but the Q
![]() $_{uw}$
(or Q
$_{uw}$
(or Q
![]() $_{vw}$
, not shown) do not. It should be noted that the thresholding operation induces some anisotropy even on perfectly isotropic Reynolds-stress tensors, because it tends to select velocity pairs along the diagonal of the quadrant plot (see figure 4
b). It can be shown by direct calculation that a threshold
$_{vw}$
, not shown) do not. It should be noted that the thresholding operation induces some anisotropy even on perfectly isotropic Reynolds-stress tensors, because it tends to select velocity pairs along the diagonal of the quadrant plot (see figure 4
b). It can be shown by direct calculation that a threshold
![]() $H=1.75$
results in
$H=1.75$
results in
![]() $\unicode[STIX]{x1D701}\approx 0.1$
for an isotropic joint-Gaussian velocity distribution with
$\unicode[STIX]{x1D701}\approx 0.1$
for an isotropic joint-Gaussian velocity distribution with
![]() $c_{uv}=0$
, and in
$c_{uv}=0$
, and in
![]() $\unicode[STIX]{x1D701}\approx 0.25$
for one with
$\unicode[STIX]{x1D701}\approx 0.25$
for one with
![]() $c_{uv}=0.4$
. This is approximately the range of
$c_{uv}=0.4$
. This is approximately the range of
![]() $\unicode[STIX]{x1D701}$
in figure 5(a). Figures 4(a) and 5(a) are consistent with a model of the flow with joint-Gaussian velocity components, in which most of the velocity cross-correlation is contained in large Q
$\unicode[STIX]{x1D701}$
in figure 5(a). Figures 4(a) and 5(a) are consistent with a model of the flow with joint-Gaussian velocity components, in which most of the velocity cross-correlation is contained in large Q
![]() $^{-}$
s.
$^{-}$
s.
Figure 5(b) further supports the distinction between small and large Qs. It shows the probability distribution of the size of the Qs defined for the three possible combinations of velocity components. They agree almost exactly below
![]() $d\approx 5L_{c}$
, and only diverge for structures above that limit. The figure also plots the size distribution for detached Qs in C2000 centred on the band of wall distances that matches the Reynolds number of M32, with similar results. The p.d.f.s of Q
$d\approx 5L_{c}$
, and only diverge for structures above that limit. The figure also plots the size distribution for detached Qs in C2000 centred on the band of wall distances that matches the Reynolds number of M32, with similar results. The p.d.f.s of Q
![]() $_{uv}$
in HST and channels have been separated into Q
$_{uv}$
in HST and channels have been separated into Q
![]() $^{+}$
and Q
$^{+}$
and Q
![]() $^{-}$
. Only the latter reach large sizes, presumably because they can grow by drawing energy from the shear. We have already mentioned that there are essentially no large Q
$^{-}$
. Only the latter reach large sizes, presumably because they can grow by drawing energy from the shear. We have already mentioned that there are essentially no large Q
![]() $^{+}$
s.
$^{+}$
s.
The conclusion from these observations is that Qs much smaller than
![]() $L_{c}$
may perhaps be useful for the study of the ‘universal’ inertial range, but they should probably be defined in terms of rotationally invariant properties of the Reynolds-stress tensor. It makes little sense to classify them into quadrants.
$L_{c}$
may perhaps be useful for the study of the ‘universal’ inertial range, but they should probably be defined in terms of rotationally invariant properties of the Reynolds-stress tensor. It makes little sense to classify them into quadrants.
Vortex clusters are almost isotropic in terms of the vorticity anisotropy tensor, and essentially identical in this respect to the flow in general. As in channels, vortex clusters in HST tend to be associated with Q
![]() $^{-}$
s. In contrast to channels, they are equally distributed between Q2s and Q4s in HST, as required by symmetry. The number fraction of co-gradient vortex clusters,
$^{-}$
s. In contrast to channels, they are equally distributed between Q2s and Q4s in HST, as required by symmetry. The number fraction of co-gradient vortex clusters,
![]() $(uv)_{m}<0$
, is approximately 60 %, almost independent of the Reynolds number and the threshold. However, the fraction of the total cluster volume contained in co-gradient vortex clusters decreases with increasing threshold, from nearly 100 % for
$(uv)_{m}<0$
, is approximately 60 %, almost independent of the Reynolds number and the threshold. However, the fraction of the total cluster volume contained in co-gradient vortex clusters decreases with increasing threshold, from nearly 100 % for
![]() $\unicode[STIX]{x1D6FC}\approx 0.1$
to approximately 70 % at the nominal
$\unicode[STIX]{x1D6FC}\approx 0.1$
to approximately 70 % at the nominal
![]() $\unicode[STIX]{x1D6FC}=1.5$
. The fastest decay occurs around the percolation crisis, and is more marked for the higher Reynolds numbers.
$\unicode[STIX]{x1D6FC}=1.5$
. The fastest decay occurs around the percolation crisis, and is more marked for the higher Reynolds numbers.

Figure 6. Average aspect ratios of the circumscribing boxes for (a) Q
![]() $^{-}$
and (b) vortex clusters, as functions of the box diagonal of the structure, scaled with the Corrsin length, for HST and channel C2000, with symbols as in table 1. The channel only includes structures whose minimum distance from the wall is
$^{-}$
and (b) vortex clusters, as functions of the box diagonal of the structure, scaled with the Corrsin length, for HST and channel C2000, with symbols as in table 1. The channel only includes structures whose minimum distance from the wall is
![]() $y^{+}>100$
, and their diagonal is scaled with
$y^{+}>100$
, and their diagonal is scaled with
![]() $L_{c}$
at the centre of gravity of the structures; ——,
$L_{c}$
at the centre of gravity of the structures; ——,
![]() $a_{xy}$
; – – –,
$a_{xy}$
; – – –,
![]() $a_{zy}$
. (c,d) Average inner and outer dimensions of the structures, as functions of their volume, for HST with symbols as in table 1. Kolmogorov scaling; ——,
$a_{zy}$
. (c,d) Average inner and outer dimensions of the structures, as functions of their volume, for HST with symbols as in table 1. Kolmogorov scaling; ——,
![]() $r_{3}$
; – – –,
$r_{3}$
; – – –,
![]() $r_{1}$
. (c) Q
$r_{1}$
. (c) Q
![]() $^{-}$
. The two dashed straight lines have slope 1.15 and 0.57 respectively. (d) Vortex clusters. The dashed straight line has slope 1.35.
$^{-}$
. The two dashed straight lines have slope 1.15 and 0.57 respectively. (d) Vortex clusters. The dashed straight line has slope 1.35.
4.3 Geometry
The shape and orientation of the structures can be characterised by the aspect ratios
![]() $a_{ij}=\unicode[STIX]{x1D6E5}_{i}/\unicode[STIX]{x1D6E5}_{j}$
, where the three
$a_{ij}=\unicode[STIX]{x1D6E5}_{i}/\unicode[STIX]{x1D6E5}_{j}$
, where the three
![]() $\unicode[STIX]{x1D6E5}_{i}$
are the dimensions of the circumscribing parallelepiped. It was found in LFJ12 that the aspect ratios of large wall-attached Q
$\unicode[STIX]{x1D6E5}_{i}$
are the dimensions of the circumscribing parallelepiped. It was found in LFJ12 that the aspect ratios of large wall-attached Q
![]() $^{-}$
s are
$^{-}$
s are
![]() $a_{xy}\approx 3$
and
$a_{xy}\approx 3$
and
![]() $a_{zy}\approx 1$
, while the smaller detached Qs are roughly isotropic. Figure 6(a) shows the aspect ratios of the Q
$a_{zy}\approx 1$
, while the smaller detached Qs are roughly isotropic. Figure 6(a) shows the aspect ratios of the Q
![]() $^{-}$
s in HST as a function of their box diagonal, scaled with the Corrsin (Reference Corrsin1958) length. The longitudinal aspect ratio
$^{-}$
s in HST as a function of their box diagonal, scaled with the Corrsin (Reference Corrsin1958) length. The longitudinal aspect ratio
![]() $a_{xy}$
increases weakly up to
$a_{xy}$
increases weakly up to
![]() $d\approx 10L_{c}\approx L_{z}$
, which is the scale at which structures begin to feel the effect of the computational box. The spanwise aspect ratio
$d\approx 10L_{c}\approx L_{z}$
, which is the scale at which structures begin to feel the effect of the computational box. The spanwise aspect ratio
![]() $a_{zy}$
decreases slowly with the size of the structures. The figure also includes data for detached structures in the channel C2000, scaled in the same way. They agree well with HST. In both cases, small structures are roughly isotropic while larger ones tend to become longer (increasing
$a_{zy}$
decreases slowly with the size of the structures. The figure also includes data for detached structures in the channel C2000, scaled in the same way. They agree well with HST. In both cases, small structures are roughly isotropic while larger ones tend to become longer (increasing
![]() $a_{xy}$
) and narrower (decreasing
$a_{xy}$
) and narrower (decreasing
![]() $a_{zy}$
), but there is a range of dimensions of approximately an order of magnitude,
$a_{zy}$
), but there is a range of dimensions of approximately an order of magnitude,
![]() $1\lesssim d/L_{c}\lesssim 10$
, in which the aspect ratios remain approximately constant and the Qs can be considered to be geometrically self-similar.
$1\lesssim d/L_{c}\lesssim 10$
, in which the aspect ratios remain approximately constant and the Qs can be considered to be geometrically self-similar.
Figure 6(b) shows the same data for vortex clusters. They behave similarly. The vortex clusters in channels tend to be slightly more elongated than the Qs, but it should be remembered that the quantities used to define vortex clusters in HST and channels are not the same.
A more intrinsic indicator of the shape of the structures is provided by the inner and outer dimensions,
![]() $r_{1}$
and
$r_{1}$
and
![]() $r_{3}$
, which are respectively the diameter of their largest inscribed and their smallest circumscribed sphere (here implemented as grid-aligned cubes). Roughly speaking,
$r_{3}$
, which are respectively the diameter of their largest inscribed and their smallest circumscribed sphere (here implemented as grid-aligned cubes). Roughly speaking,
![]() $r_{3}$
is the diameter of the structure, which typically coincides in our case with
$r_{3}$
is the diameter of the structure, which typically coincides in our case with
![]() $\unicode[STIX]{x1D6E5}_{x}$
, and
$\unicode[STIX]{x1D6E5}_{x}$
, and
![]() $r_{1}$
is the thickness of the constituent substructures. These dimensions were used by Catrakis & Dimotakis (Reference Catrakis and Dimotakis1996), Moisy & Jiménez (Reference Moisy and Jiménez2004) and LFJ12 to characterise structures in various turbulent flows. A third dimension can be defined from the volume of the structure as
$r_{1}$
is the thickness of the constituent substructures. These dimensions were used by Catrakis & Dimotakis (Reference Catrakis and Dimotakis1996), Moisy & Jiménez (Reference Moisy and Jiménez2004) and LFJ12 to characterise structures in various turbulent flows. A third dimension can be defined from the volume of the structure as
![]() $r_{2}=V/r_{1}r_{3}$
, and can be used to classify simple shapes (Moisy & Jiménez Reference Moisy and Jiménez2004), but its meaning in very irregular shapes is unclear. The two intrinsic dimensions of Q
$r_{2}=V/r_{1}r_{3}$
, and can be used to classify simple shapes (Moisy & Jiménez Reference Moisy and Jiménez2004), but its meaning in very irregular shapes is unclear. The two intrinsic dimensions of Q
![]() $^{-}$
s and vortex clusters in HST are given in figure 6(c,d) as functions of the structure volume. They follow fairly good power laws, especially for the higher Reynolds numbers. It should be noted that
$^{-}$
s and vortex clusters in HST are given in figure 6(c,d) as functions of the structure volume. They follow fairly good power laws, especially for the higher Reynolds numbers. It should be noted that
![]() $r_{3}\sim V^{\unicode[STIX]{x1D6FE}/3}$
can be rewritten as
$r_{3}\sim V^{\unicode[STIX]{x1D6FE}/3}$
can be rewritten as
![]() $V\sim r_{3}^{3/\unicode[STIX]{x1D6FE}}$
, which can be interpreted as a statistical estimate,
$V\sim r_{3}^{3/\unicode[STIX]{x1D6FE}}$
, which can be interpreted as a statistical estimate,
![]() $D_{f}=3/\unicode[STIX]{x1D6FE}$
, of the fractal dimension of the set of structures within a given family (LFJ12). Figures 6(c) and 6(d) imply
$D_{f}=3/\unicode[STIX]{x1D6FE}$
, of the fractal dimension of the set of structures within a given family (LFJ12). Figures 6(c) and 6(d) imply
![]() $D_{f}=2.6$
for Q
$D_{f}=2.6$
for Q
![]() $^{-}$
and
$^{-}$
and
![]() $D_{f}=2.2$
for vortex clusters. These are slightly higher than the estimates in LFJ12 for channels (2.3 and 2.0 respectively), but the difference is consistent with the fairly broad distributions that are obtained when estimating the fractal dimensions of individual structures by various methods.
$D_{f}=2.2$
for vortex clusters. These are slightly higher than the estimates in LFJ12 for channels (2.3 and 2.0 respectively), but the difference is consistent with the fairly broad distributions that are obtained when estimating the fractal dimensions of individual structures by various methods.
A consequence of figure 6(c,d) is that the bounding box of all of the structures is fairly empty, and becomes emptier for the larger volumes. Thus, if we define a ‘fill fraction’ as
![]() $V/r_{3}^{3}$
, it varies from approximately 0.1 for the smallest Qs and vortex clusters to
$V/r_{3}^{3}$
, it varies from approximately 0.1 for the smallest Qs and vortex clusters to
![]() $3\times 10^{-3}$
and
$3\times 10^{-3}$
and
![]() $3\times 10^{-4}$
respectively for the largest ones.
$3\times 10^{-4}$
respectively for the largest ones.
The inner dimension of vortex clusters in figure 6(d) is
![]() $r_{1}\approx 6\unicode[STIX]{x1D702}$
, independently of the cluster volume, which approximately agrees with the diameter of individual filamentary vortices in turbulence (Jiménez & Wray Reference Jiménez and Wray1998; Tanahashi, Iwase & Miyauchi Reference Tanahashi, Iwase and Miyauchi2001; del Álamo et al. Reference del Álamo, Jiménez, Zandonade and Moser2006; Pirozzoli, Bernardini & Grasso Reference Pirozzoli, Bernardini and Grasso2008; Stanislas, Perret & Foucaut Reference Stanislas, Perret and Foucaut2008). It is also consistent with the description of vortex clusters as ‘sponges of strings’ (LFJ12).
$r_{1}\approx 6\unicode[STIX]{x1D702}$
, independently of the cluster volume, which approximately agrees with the diameter of individual filamentary vortices in turbulence (Jiménez & Wray Reference Jiménez and Wray1998; Tanahashi, Iwase & Miyauchi Reference Tanahashi, Iwase and Miyauchi2001; del Álamo et al. Reference del Álamo, Jiménez, Zandonade and Moser2006; Pirozzoli, Bernardini & Grasso Reference Pirozzoli, Bernardini and Grasso2008; Stanislas, Perret & Foucaut Reference Stanislas, Perret and Foucaut2008). It is also consistent with the description of vortex clusters as ‘sponges of strings’ (LFJ12).
The inner dimension of the Qs in figure 6(c),
![]() $r_{1}\sim (\unicode[STIX]{x1D702}r_{3})^{1/2}$
, is more interesting because it depends on the volume, and is therefore a property of the structures rather than of the flow. These structures are described in LFJ12 as ‘sponges of flakes’, mainly from visual observation and from their relatively high fractal dimension. It follows from the definition of
$r_{1}\sim (\unicode[STIX]{x1D702}r_{3})^{1/2}$
, is more interesting because it depends on the volume, and is therefore a property of the structures rather than of the flow. These structures are described in LFJ12 as ‘sponges of flakes’, mainly from visual observation and from their relatively high fractal dimension. It follows from the definition of
![]() $r_{2}$
and from the power laws in figure 6(c) that
$r_{2}$
and from the power laws in figure 6(c) that
![]() $r_{2}\sim r_{3}$
in Qs, which also suggests flakes (see figure 3
a). A rough model that at least reproduces the functional dependence of
$r_{2}\sim r_{3}$
in Qs, which also suggests flakes (see figure 3
a). A rough model that at least reproduces the functional dependence of
![]() $r_{1}$
can be constructed if we interpret these flakes as viscosity-dominated layers of thickness
$r_{1}$
can be constructed if we interpret these flakes as viscosity-dominated layers of thickness
![]() $r_{1}$
. We know from the definition of Qs that the velocity difference across them is of the order of
$r_{1}$
. We know from the definition of Qs that the velocity difference across them is of the order of
![]() $u^{\prime }$
, so that we can approximate the resulting structure-dependent mean strain as
$u^{\prime }$
, so that we can approximate the resulting structure-dependent mean strain as
![]() $s\approx u^{\prime }/r_{3}$
in a coarse-grained sense. Some algebra shows that the corresponding viscous equilibrium thickness is
$s\approx u^{\prime }/r_{3}$
in a coarse-grained sense. Some algebra shows that the corresponding viscous equilibrium thickness is
![]() $r_{1}=(\unicode[STIX]{x1D708}/s)^{1/2}\approx (\unicode[STIX]{x1D708}/u^{\prime }\unicode[STIX]{x1D702})^{1/2}(\unicode[STIX]{x1D702}r_{3})^{1/2}$
. The prefactor in this estimate is proportional to
$r_{1}=(\unicode[STIX]{x1D708}/s)^{1/2}\approx (\unicode[STIX]{x1D708}/u^{\prime }\unicode[STIX]{x1D702})^{1/2}(\unicode[STIX]{x1D702}r_{3})^{1/2}$
. The prefactor in this estimate is proportional to
![]() $Re_{\unicode[STIX]{x1D706}}^{-1/4}$
, and varies between 0.28 and 0.4 in our DNS. The lower dashed line in figure 6(c) is drawn with a prefactor 0.35 and, given the qualitative nature of the above argument, agrees reasonably well with the measured
$Re_{\unicode[STIX]{x1D706}}^{-1/4}$
, and varies between 0.28 and 0.4 in our DNS. The lower dashed line in figure 6(c) is drawn with a prefactor 0.35 and, given the qualitative nature of the above argument, agrees reasonably well with the measured
![]() $r_{1}$
.
$r_{1}$
.
It is clear that this argument can only be approximate, particularly regarding the estimation of the driving strain. It follows from well-known integral constraints that the predominant strain in turbulence is of the order of
![]() $\unicode[STIX]{x1D714}^{\prime }\sim u^{\prime }/\unicode[STIX]{x1D706}$
, and that the associated viscous length is the Kolmogorov scale
$\unicode[STIX]{x1D714}^{\prime }\sim u^{\prime }/\unicode[STIX]{x1D706}$
, and that the associated viscous length is the Kolmogorov scale
![]() $\unicode[STIX]{x1D702}$
(Pope Reference Pope2000). However, Hunt, Eames & Westerweel (Reference Hunt, Eames and Westerweel2006) argued that strong shear layers exclude the small-scale strain, leaving only the strain associated with the depth of the layer. In our case, the thresholding operation used to define the structures guarantees that they represent relatively strong velocity gradients, but we will see in § 5 that Qs only have velocity differences of order
$\unicode[STIX]{x1D702}$
(Pope Reference Pope2000). However, Hunt, Eames & Westerweel (Reference Hunt, Eames and Westerweel2006) argued that strong shear layers exclude the small-scale strain, leaving only the strain associated with the depth of the layer. In our case, the thresholding operation used to define the structures guarantees that they represent relatively strong velocity gradients, but we will see in § 5 that Qs only have velocity differences of order
![]() $u^{\prime }$
across their largest dimension, if at all, justifying our strain estimate in the previous paragraph. Smaller corrugations, such as those of size
$u^{\prime }$
across their largest dimension, if at all, justifying our strain estimate in the previous paragraph. Smaller corrugations, such as those of size
![]() $O(r_{1})$
, correspond to weaker local velocity fluctuations that happen to cross the sharp threshold used in the identification. In the limit of very large structures, with
$O(r_{1})$
, correspond to weaker local velocity fluctuations that happen to cross the sharp threshold used in the identification. In the limit of very large structures, with
![]() $r_{3}\sim L_{\unicode[STIX]{x1D700}}$
, the previous estimate becomes
$r_{3}\sim L_{\unicode[STIX]{x1D700}}$
, the previous estimate becomes
![]() $r_{1}\sim \unicode[STIX]{x1D706}$
, and the argument reduces to the one in Hunt et al. (Reference Hunt, Eames and Westerweel2006), but the present results require extension of the analysis to the full range of scales.
$r_{1}\sim \unicode[STIX]{x1D706}$
, and the argument reduces to the one in Hunt et al. (Reference Hunt, Eames and Westerweel2006), but the present results require extension of the analysis to the full range of scales.

Figure 7. (a) Probability density function of the aspect ratio
![]() $a_{xy}$
of Q
$a_{xy}$
of Q
![]() $^{-}$
s in C2000 as a function of their minimum distance from the wall. Each vertical section is the individual p.d.f. at one wall distance. Contours contain 50 % and 95 % of the data; –▵–, Average aspect ratio. The vertical dashed line is
$^{-}$
s in C2000 as a function of their minimum distance from the wall. Each vertical section is the individual p.d.f. at one wall distance. Contours contain 50 % and 95 % of the data; –▵–, Average aspect ratio. The vertical dashed line is
![]() $y_{min}^{+}=20$
. Symbols are the mean and standard deviation of
$y_{min}^{+}=20$
. Symbols are the mean and standard deviation of
![]() $a_{xy}$
in HST, as in table 1. They are plotted at arbitrary
$a_{xy}$
in HST, as in table 1. They are plotted at arbitrary
![]() $y$
locations. (b) As in (a), for
$y$
locations. (b) As in (a), for
![]() $a_{zy}$
. (c) Sketch of the root and body of a large attached Q2. Flow is from left to right, and the Q2 is qualitatively coloured with the distance from the wall. (d) Average
$a_{zy}$
. (c) Sketch of the root and body of a large attached Q2. Flow is from left to right, and the Q2 is qualitatively coloured with the distance from the wall. (d) Average
![]() $a_{xz}$
of Q
$a_{xz}$
of Q
![]() $^{-}$
s with
$^{-}$
s with
![]() $y_{min}^{+}<100$
in C2000, as a function of their vertical dimension. See the sketch in (c) for definitions; ——,
$y_{min}^{+}<100$
in C2000, as a function of their vertical dimension. See the sketch in (c) for definitions; ——,
![]() $\unicode[STIX]{x1D6E5}_{x}/\unicode[STIX]{x1D6E5}_{z}$
; – – –,
$\unicode[STIX]{x1D6E5}_{x}/\unicode[STIX]{x1D6E5}_{z}$
; – – –,
![]() $\unicode[STIX]{x1D6E5}_{x,100}/\unicode[STIX]{x1D6E5}_{z}$
; - - - -,
$\unicode[STIX]{x1D6E5}_{x,100}/\unicode[STIX]{x1D6E5}_{z}$
; - - - -,
![]() $(\unicode[STIX]{x1D6E5}_{x}-\unicode[STIX]{x1D6E5}_{x,100})^{+}=100$
; – ⋅ – ⋅ –,
$(\unicode[STIX]{x1D6E5}_{x}-\unicode[STIX]{x1D6E5}_{x,100})^{+}=100$
; – ⋅ – ⋅ –,
![]() $\unicode[STIX]{x1D6E5}_{x,100}/\unicode[STIX]{x1D6E5}_{z}$
for Q
$\unicode[STIX]{x1D6E5}_{x,100}/\unicode[STIX]{x1D6E5}_{z}$
for Q
![]() $^{-}$
s constructed from points above
$^{-}$
s constructed from points above
![]() $y^{+}=100$
. The short horizontal dashed line is
$y^{+}=100$
. The short horizontal dashed line is
![]() $a_{xz}=1.27$
, as in the detached and HST structures.
$a_{xz}=1.27$
, as in the detached and HST structures.
4.4 Attached versus detached eddies in channels
Up to now, we have compared the structures in HST with the detached eddies in channels. Most large eddies in channels are attached, because the wall limits how high they can grow but not their wall-parallel dimensions (Townsend Reference Townsend1961). Attached and detached eddies behave differently, particularly in their geometry. It was shown in LFJ12 that attached Q
![]() $^{-}$
s in channels have
$^{-}$
s in channels have
![]() $a_{xy}\approx 3$
, while we have seen that those in HST have
$a_{xy}\approx 3$
, while we have seen that those in HST have
![]() $a_{xy}\approx 1.2$
. The higher elongations of the largest channel eddies in figures 6(a) and 6(b) correspond to attached structures.
$a_{xy}\approx 1.2$
. The higher elongations of the largest channel eddies in figures 6(a) and 6(b) correspond to attached structures.
The origin of this higher elongation is explored in figure 7(a), which contains the p.d.f. of
![]() $a_{xy}$
in C2000 as a function of the minimum distance of the structures from the wall. This is the distance originally used in AJZM06 to differentiate between attached and detached objects. The figure shows that only strictly attached structures
$a_{xy}$
in C2000 as a function of the minimum distance of the structures from the wall. This is the distance originally used in AJZM06 to differentiate between attached and detached objects. The figure shows that only strictly attached structures
![]() $(y_{min}^{+}\lesssim 20)$
are elongated. Those farther from the wall have elongations very similar to those in HST. Interestingly, figure 7(b) shows that
$(y_{min}^{+}\lesssim 20)$
are elongated. Those farther from the wall have elongations very similar to those in HST. Interestingly, figure 7(b) shows that
![]() $a_{zy}$
is similar for attached and detached Qs, in agreement with the observation by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) that large attached Qs grow predominantly by merging with other eddies in front and behind, but not sideways.
$a_{zy}$
is similar for attached and detached Qs, in agreement with the observation by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) that large attached Qs grow predominantly by merging with other eddies in front and behind, but not sideways.
The relatively good scaling of figures 6(a) and 6(b) with
![]() $L_{c}$
suggests that the elongation of the structures is a consequence of their interaction with the mean shear. It was shown by Corrsin (Reference Corrsin1958) that the relevant parameter is
$L_{c}$
suggests that the elongation of the structures is a consequence of their interaction with the mean shear. It was shown by Corrsin (Reference Corrsin1958) that the relevant parameter is
![]() $S^{\ast }=Sq^{2}/\unicode[STIX]{x1D700}$
, which measures the ratio between the eddy turnover and the shear deformation time. When
$S^{\ast }=Sq^{2}/\unicode[STIX]{x1D700}$
, which measures the ratio between the eddy turnover and the shear deformation time. When
![]() $S^{\ast }\gg 1$
, the structures are controlled by the shear, but for lower
$S^{\ast }\gg 1$
, the structures are controlled by the shear, but for lower
![]() $S^{\ast }$
, nonlinear effects isotropise them. Jiménez (Reference Jiménez2013b
) showed that
$S^{\ast }$
, nonlinear effects isotropise them. Jiménez (Reference Jiménez2013b
) showed that
![]() $S^{\ast }$
is everywhere moderate in channels except for
$S^{\ast }$
is everywhere moderate in channels except for
![]() $y^{+}\lesssim 25$
, where it grows to
$y^{+}\lesssim 25$
, where it grows to
![]() $S^{\ast }\approx 40$
. The origin of the large elongation of attached Qs in channels could thus be the high
$S^{\ast }\approx 40$
. The origin of the large elongation of attached Qs in channels could thus be the high
![]() $S^{\ast }$
in the viscous layer. In fact, it was shown by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) that large attached Qs have two components with different properties: a coherent one above
$S^{\ast }$
in the viscous layer. In fact, it was shown by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) that large attached Qs have two components with different properties: a coherent one above
![]() $y^{+}\approx 100$
which approximately advects with the local mean velocity and a more elongated ‘root’ near the wall whose small-scale features move at a different velocity from the structure itself, and which is constantly being shredded by the shear and recreated by viscosity (see the sketch in figure 7
c). However, it is difficult to distinguish between the averaged properties of the flow within attached and detached eddies, both of which can be described by the joint-Gaussian model discussed in figure 4. Even if the buffer layer behaves differently from the rest of the flow, it constitutes too small a part of the large attached eddies to influence their statistics.
$y^{+}\approx 100$
which approximately advects with the local mean velocity and a more elongated ‘root’ near the wall whose small-scale features move at a different velocity from the structure itself, and which is constantly being shredded by the shear and recreated by viscosity (see the sketch in figure 7
c). However, it is difficult to distinguish between the averaged properties of the flow within attached and detached eddies, both of which can be described by the joint-Gaussian model discussed in figure 4. Even if the buffer layer behaves differently from the rest of the flow, it constitutes too small a part of the large attached eddies to influence their statistics.
Whether the near-wall region, as opposed to the viscous sublayer, is responsible for the higher elongation of the attached Q
![]() $^{-}$
s is tested in figure 7(d), which compares
$^{-}$
s is tested in figure 7(d), which compares
![]() $a_{xz}$
for the attached eddies as functions of the overall eddy height, computed in three different ways. The solid line represents all of the large attached Q
$a_{xz}$
for the attached eddies as functions of the overall eddy height, computed in three different ways. The solid line represents all of the large attached Q
![]() $^{-}$
s, defined for this particular figure as those with
$^{-}$
s, defined for this particular figure as those with
![]() $y_{min}^{+}<100$
. The triangles are the dimensions of the part of those same attached eddies that extends above
$y_{min}^{+}<100$
. The triangles are the dimensions of the part of those same attached eddies that extends above
![]() $y^{+}=100$
. They therefore subtract the effect of the near-wall region (figure 7
c), and show that relatively small attached eddies owe the higher elongation to the root. Their upper coherent component has an aspect ratio similar to those of detached eddies, but this effect decreases for larger structures and is negligible for the largest ones. The dashed line in figure 7(d) is a model in which the extra elongation is approximated by a fixed extra length
$y^{+}=100$
. They therefore subtract the effect of the near-wall region (figure 7
c), and show that relatively small attached eddies owe the higher elongation to the root. Their upper coherent component has an aspect ratio similar to those of detached eddies, but this effect decreases for larger structures and is negligible for the largest ones. The dashed line in figure 7(d) is a model in which the extra elongation is approximated by a fixed extra length
![]() $\unicode[STIX]{x1D6E5}_{x}^{+}=100$
, and fits the data reasonably well. This is the order of magnitude of the size of the minimal buffer-layer flow unit (Jiménez & Moin Reference Jiménez and Moin1991), suggesting that the near-wall root is formed by multiple such units underneath the coherent outer component, some of which accidentally stick in front of or behind it. Visual inspection of individual structures confirms that this is a reasonable description (see, for example, figures 8 and 12 in LFJ12). Since these minimal structures have a fixed size in viscous units, their effect on the large eddies that reach into the logarithmic and outer layers is negligible.
$\unicode[STIX]{x1D6E5}_{x}^{+}=100$
, and fits the data reasonably well. This is the order of magnitude of the size of the minimal buffer-layer flow unit (Jiménez & Moin Reference Jiménez and Moin1991), suggesting that the near-wall root is formed by multiple such units underneath the coherent outer component, some of which accidentally stick in front of or behind it. Visual inspection of individual structures confirms that this is a reasonable description (see, for example, figures 8 and 12 in LFJ12). Since these minimal structures have a fixed size in viscous units, their effect on the large eddies that reach into the logarithmic and outer layers is negligible.
Because of the way in which attached Qs have been defined in the previous paragraph, the points forming the truncated and attached Qs above
![]() $y^{+}=100$
are the same, although clustered in different ways. The chain-dotted line in figure 7(d) also refers to the dimensions of eddies measured above
$y^{+}=100$
are the same, although clustered in different ways. The chain-dotted line in figure 7(d) also refers to the dimensions of eddies measured above
![]() $y^{+}=100$
, but for Qs that have been computed using only points above that level. There is no way to know whether some of these truncated Qs are connected below
$y^{+}=100$
, but for Qs that have been computed using only points above that level. There is no way to know whether some of these truncated Qs are connected below
![]() $y^{+}=100$
, and the difference between the chain-dotted line and the triangles measures the importance of those ‘hidden’ near-wall connections. It is clear that the truncated Qs cannot be longer than the full ones, but it is interesting that the shortening increases with the size of the eddy. While the difference in length is
$y^{+}=100$
, and the difference between the chain-dotted line and the triangles measures the importance of those ‘hidden’ near-wall connections. It is clear that the truncated Qs cannot be longer than the full ones, but it is interesting that the shortening increases with the size of the eddy. While the difference in length is
![]() $\unicode[STIX]{x1D6E5}_{x}^{+}\approx 0$
for the smallest eddies, it grows to
$\unicode[STIX]{x1D6E5}_{x}^{+}\approx 0$
for the smallest eddies, it grows to
![]() $\unicode[STIX]{x1D6E5}_{x}^{+}\approx 1500$
for the tallest ones at the right end of the figure, which is approximately 20 % of their total length.
$\unicode[STIX]{x1D6E5}_{x}^{+}\approx 1500$
for the tallest ones at the right end of the figure, which is approximately 20 % of their total length.
The implied model is that large Qs in the channel grow until they hit the wall. Once they do, the outer part of the eddy keeps growing in length and width but not in height, as its bottom is continually truncated by the high shear at the wall and by viscosity. At the same time, the elongation of the attached eddies increases because they tend to get ‘spuriously’ connected near the wall. That the largest attached eddies owe part of their size to spurious connections near the wall was already noted by LFJ12.
In the rest of the paper, we will mostly restrict ourselves to comparisons of HST with detached eddies in channels, particularly with those with
![]() $y_{min}^{+}\geqslant 100$
.
$y_{min}^{+}\geqslant 100$
.
5 Spatial organisation
The relative position of tall attached structures was studied for channels by LFJ12, who concluded that they group into spanwise pairs of a Q2 and a Q4, and that the pairs are arranged in streamwise trains, roughly associated with the large-scale streamwise-velocity streaks. Vortex clusters tend to be located in the gap between the two components of the pair, predominately associated with the Q2. In the following, we repeat their analysis for HST, in part to compare the two flows, but also because HST allows us to extend the study to the third dimension without interference from the wall. In particular, we have seen that the symmetry of HST precludes the preferential association of the vortex clusters with only one flavour of Q
![]() $^{-}$
, and we expect to find more symmetric composite structures in HST than in channels. We define three-dimensional joint p.d.f.s,
$^{-}$
, and we expect to find more symmetric composite structures in HST than in channels. We define three-dimensional joint p.d.f.s,
![]() $p^{ij}(\unicode[STIX]{x1D6FF}_{x},\unicode[STIX]{x1D6FF}_{y},\unicode[STIX]{x1D6FF}_{z})$
, of the relative distances between structures of type
$p^{ij}(\unicode[STIX]{x1D6FF}_{x},\unicode[STIX]{x1D6FF}_{y},\unicode[STIX]{x1D6FF}_{z})$
, of the relative distances between structures of type
![]() $j$
with respect to
$j$
with respect to
![]() $i$
, where
$i$
, where
![]() $i=2$
refers to Q2s,
$i=2$
refers to Q2s,
![]() $i=4$
refers to Q4s and
$i=4$
refers to Q4s and
![]() $i=C$
to vortex clusters. The vector of relative distances is defined as
$i=C$
to vortex clusters. The vector of relative distances is defined as
where
![]() $\boldsymbol{x}_{c}^{(i)}$
and
$\boldsymbol{x}_{c}^{(i)}$
and
![]() $d^{(i)}$
are respectively the centre of gravity and the diagonal length of the circumscribing box. We only consider two structures as related if their sizes are similar enough to satisfy
$d^{(i)}$
are respectively the centre of gravity and the diagonal length of the circumscribing box. We only consider two structures as related if their sizes are similar enough to satisfy
In channels, LFJ12 use a condition on the height of the centre of gravity of attached structures instead of (5.2), and only study relative positions in the
![]() $(x,z)$
plane. It can be shown that their criterion implies
$(x,z)$
plane. It can be shown that their criterion implies
![]() $|\unicode[STIX]{x1D6FF}_{y}|\lesssim 0.2$
. We have recomputed their results using (5.2) and three-dimensional positions, but, for the sake of comparison and to improve statistics, all of the two-dimensional sections of our three-dimensional p.d.f.s are presented averaged over slabs of thickness
$|\unicode[STIX]{x1D6FF}_{y}|\lesssim 0.2$
. We have recomputed their results using (5.2) and three-dimensional positions, but, for the sake of comparison and to improve statistics, all of the two-dimensional sections of our three-dimensional p.d.f.s are presented averaged over slabs of thickness
![]() $\unicode[STIX]{x1D6FF}=\pm 0.2$
normal to the plane of the plot.
$\unicode[STIX]{x1D6FF}=\pm 0.2$
normal to the plane of the plot.
For the purpose of this section, we disregard structures that are ‘infinite’ in the sense that their size in any direction equals that of the simulation box, because their centre of gravity is not well defined. They are much more common in HST simulations than in channels because of the minimal simulation box. For the same reason, the distance between structures is limited to
![]() $[-L_{x}/2:L_{x}/2]\times [-L_{y}/2:L_{y}/2]\times [-L_{z}/2:L_{z}/2]$
, which is implemented by copying, translating and shifting structures whenever they cross the boundaries of the fundamental simulation box. To test the soundness of this procedure, we repeated the analysis of case L38, whose vertical dimension is not minimal, considering only structures with
$[-L_{x}/2:L_{x}/2]\times [-L_{y}/2:L_{y}/2]\times [-L_{z}/2:L_{z}/2]$
, which is implemented by copying, translating and shifting structures whenever they cross the boundaries of the fundamental simulation box. To test the soundness of this procedure, we repeated the analysis of case L38, whose vertical dimension is not minimal, considering only structures with
![]() $y_{c}\in [L_{y}/3:2L_{y}/3]$
relative to those with
$y_{c}\in [L_{y}/3:2L_{y}/3]$
relative to those with
![]() $y_{c}\in [0:L_{y}]$
, without using the shifted periodicity in
$y_{c}\in [0:L_{y}]$
, without using the shifted periodicity in
![]() $y$
. The results did not change.
$y$
. The results did not change.
Finally, to simplify the presentation, we will not generally use case L38 from now on. We have seen on several occasions that its Reynolds number is comparable to the buffer layer in channels, rather than to the logarithmic or outer layers, complicating comparisons between the two flows. However, to confirm that its differences from the other HST cases are a Reynolds number effect, rather than due to its different vertical aspect ratio, most of the analysis was repeated for some simulations not otherwise used in this paper. Two low-Reynolds-number cases
![]() $(Re_{\unicode[STIX]{x1D706}}=50)$
in flatter boxes, L32
$(Re_{\unicode[STIX]{x1D706}}=50)$
in flatter boxes, L32
![]() $(A_{yz}=2)$
and L34
$(A_{yz}=2)$
and L34
![]() $(A_{yz}=4)$
, behaved as L38. A higher-Reynolds-number case in a taller box (
$(A_{yz}=4)$
, behaved as L38. A higher-Reynolds-number case in a taller box (
![]() $A_{yz}=4,Re_{\unicode[STIX]{x1D706}}=100$
) behaved as M32 or H32.
$A_{yz}=4,Re_{\unicode[STIX]{x1D706}}=100$
) behaved as M32 or H32.

Figure 8. (a) Average distance between closest pairs of Qs of the same kind,
![]() $r^{(44)}$
, defined as in (5.1), as a function of the diagonal size of the reference structure. The dashed line is
$r^{(44)}$
, defined as in (5.1), as a function of the diagonal size of the reference structure. The dashed line is
![]() $r^{(44)}\approx d$
. (b,c) Three-dimensional p.d.f. of the relative distance between eddies of the same kind in M32 with
$r^{(44)}\approx d$
. (b,c) Three-dimensional p.d.f. of the relative distance between eddies of the same kind in M32 with
![]() $d<4L_{c}$
. (b) Streamwise
$d<4L_{c}$
. (b) Streamwise
![]() $(\unicode[STIX]{x1D6FF}_{z}=0)$
cross-section of the p.d.f.,
$(\unicode[STIX]{x1D6FF}_{z}=0)$
cross-section of the p.d.f.,
![]() $p^{44}(\unicode[STIX]{x1D6FF}_{x},\unicode[STIX]{x1D6FF}_{y})$
, integrated over
$p^{44}(\unicode[STIX]{x1D6FF}_{x},\unicode[STIX]{x1D6FF}_{y})$
, integrated over
![]() $\unicode[STIX]{x1D6FF}=\pm 0.2$
normal to the plane of the plot. (c) Three-dimensional
$\unicode[STIX]{x1D6FF}=\pm 0.2$
normal to the plane of the plot. (c) Three-dimensional
![]() $p^{44}$
, as in (b). The black arrow at the centre of the box is the nominal velocity for a Q4. Those at the two maxima of the p.d.f. are also Q4s, and reinforce the central one, suggesting a mechanism by which the p.d.f. is concentrated at those locations. (d) The p.d.f.
$p^{44}$
, as in (b). The black arrow at the centre of the box is the nominal velocity for a Q4. Those at the two maxima of the p.d.f. are also Q4s, and reinforce the central one, suggesting a mechanism by which the p.d.f. is concentrated at those locations. (d) The p.d.f.
![]() $p^{11}(\unicode[STIX]{x1D6FF}_{x},\unicode[STIX]{x1D6FF}_{y})$
for
$p^{11}(\unicode[STIX]{x1D6FF}_{x},\unicode[STIX]{x1D6FF}_{y})$
for
![]() $d<4L_{c}$
. The contours and isosurfaces in (b–d) contain the highest 15 % of the data. In all cases, open symbols are for Q
$d<4L_{c}$
. The contours and isosurfaces in (b–d) contain the highest 15 % of the data. In all cases, open symbols are for Q
![]() $_{uv}$
: ▫, M32; ○, H32; ▵, Qs in C2000 with
$_{uv}$
: ▫, M32; ○, H32; ▵, Qs in C2000 with
![]() $y_{min}^{+}\geqslant 100$
. The closed squares are Q
$y_{min}^{+}\geqslant 100$
. The closed squares are Q
![]() $_{uw}$
in M32, in which case the vertical axis is
$_{uw}$
in M32, in which case the vertical axis is
![]() $\unicode[STIX]{x1D6FF}_{z}$
. (e) Mean streamwise velocity
$\unicode[STIX]{x1D6FF}_{z}$
. (e) Mean streamwise velocity
![]() $\{u\}$
, conditioned to the presence of a pair of neighbouring Q4s in the coordinates (5.3). Case M32. The coloured background is
$\{u\}$
, conditioned to the presence of a pair of neighbouring Q4s in the coordinates (5.3). Case M32. The coloured background is
![]() $\{u\}^{+}\in (0,\,1.5)$
, from light to dark. The white contours are 0.8 the maximum of the p.d.f. of the position of the points in the two members of the pair.
$\{u\}^{+}\in (0,\,1.5)$
, from light to dark. The white contours are 0.8 the maximum of the p.d.f. of the position of the points in the two members of the pair.
5.1 Relative positions of structures of the same kind
Figure 8(a) displays the mean value of the absolute distance,
![]() $r^{(ii)}=|\boldsymbol{r}^{(ii)}|$
(no summation), from a Q to its closest Q of the same kind, as a function of the box diagonal of the reference structure. Below
$r^{(ii)}=|\boldsymbol{r}^{(ii)}|$
(no summation), from a Q to its closest Q of the same kind, as a function of the box diagonal of the reference structure. Below
![]() $d\approx 50\unicode[STIX]{x1D702}$
, the mean distance is constant,
$d\approx 50\unicode[STIX]{x1D702}$
, the mean distance is constant,
![]() $r^{(44)}\approx 50\unicode[STIX]{x1D702}$
, which is roughly the wavelength of the maximum of the dissipation spectrum in most turbulent flows (Jiménez Reference Jiménez2013b
). This is also the size of the structures in the dissipative end of the turbulence spectrum that were shown by Yoshida, Yamaguchi & Kaneda (Reference Yoshida, Yamaguchi and Kaneda2005) to be enslaved to the larger inertial ones. They are essentially Kolmogorov viscous eddies, and the figure shows that they are densely packed on average, separated by other eddies of similar size. Above
$r^{(44)}\approx 50\unicode[STIX]{x1D702}$
, which is roughly the wavelength of the maximum of the dissipation spectrum in most turbulent flows (Jiménez Reference Jiménez2013b
). This is also the size of the structures in the dissipative end of the turbulence spectrum that were shown by Yoshida, Yamaguchi & Kaneda (Reference Yoshida, Yamaguchi and Kaneda2005) to be enslaved to the larger inertial ones. They are essentially Kolmogorov viscous eddies, and the figure shows that they are densely packed on average, separated by other eddies of similar size. Above
![]() $d\approx 50\unicode[STIX]{x1D702}$
, the distance to the closest comparable structure is
$d\approx 50\unicode[STIX]{x1D702}$
, the distance to the closest comparable structure is
![]() $r^{(44)}\approx d$
up to the largest available scale,
$r^{(44)}\approx d$
up to the largest available scale,
![]() $d\approx L_{\unicode[STIX]{x1D700}}$
. These are the self-similar inertial eddies, and they are also densely packed. It follows from their definition that the velocity fluctuations in Qs are
$d\approx L_{\unicode[STIX]{x1D700}}$
. These are the self-similar inertial eddies, and they are also densely packed. It follows from their definition that the velocity fluctuations in Qs are
![]() $O(u^{\prime })$
with respect to the mean, but the velocity difference between neighbouring structures need not be of the same order. The close packing of Qs of the same kind suggests that they are pieces of larger structures. The Reynolds stress of the composite structure is
$O(u^{\prime })$
with respect to the mean, but the velocity difference between neighbouring structures need not be of the same order. The close packing of Qs of the same kind suggests that they are pieces of larger structures. The Reynolds stress of the composite structure is
![]() $O({u^{\prime }}^{2})$
, as required by the identification procedure, but the isosurface bounding it can become broken into smaller pieces when the Reynolds stress fluctuates slightly above or below the chosen threshold.
$O({u^{\prime }}^{2})$
, as required by the identification procedure, but the isosurface bounding it can become broken into smaller pieces when the Reynolds stress fluctuates slightly above or below the chosen threshold.
Figure 8(b) displays two-dimensional p.d.f.s of the relative position of neighbouring ‘small’ Q4s
![]() $(d<4L_{c})$
. In channels, attached Qs are arranged streamwise in the
$(d<4L_{c})$
. In channels, attached Qs are arranged streamwise in the
![]() $(x,z)$
plane (LFJ12). This is still true in HST, but, in addition, the p.d.f. is inclined downwards in the streamwise direction. It should be noted that the p.d.f.s included for detached Qs in the channel agree well with HST, and are also inclined downwards. Because of the symmetry of HST, the same inclination is found for Q2s in HST. The downward tilt of the Q2s is slightly less marked in the channels (not shown); apparently, even these relatively small detached Qs are influenced by the wall or by the inhomogeneity of the mean shear. Also not shown is the p.d.f. of the relative position of neighbouring large Q4s
$(x,z)$
plane (LFJ12). This is still true in HST, but, in addition, the p.d.f. is inclined downwards in the streamwise direction. It should be noted that the p.d.f.s included for detached Qs in the channel agree well with HST, and are also inclined downwards. Because of the symmetry of HST, the same inclination is found for Q2s in HST. The downward tilt of the Q2s is slightly less marked in the channels (not shown); apparently, even these relatively small detached Qs are influenced by the wall or by the inhomogeneity of the mean shear. Also not shown is the p.d.f. of the relative position of neighbouring large Q4s
![]() $(d\geqslant 4L_{c})$
. It is still true that these eddies are aligned streamwise, but the downwards inclination is less marked than for the small structures, presumably reflecting the anisotropy of the large-scale velocities. As we saw in the discussion of figures 4(a) and 5(a),
$(d\geqslant 4L_{c})$
. It is still true that these eddies are aligned streamwise, but the downwards inclination is less marked than for the small structures, presumably reflecting the anisotropy of the large-scale velocities. As we saw in the discussion of figures 4(a) and 5(a),
![]() $u$
is the predominant velocity component, and the flow anisotropy is mainly associated with the largest structures.
$u$
is the predominant velocity component, and the flow anisotropy is mainly associated with the largest structures.
A three-dimensional view of
![]() $p^{44}(\unicode[STIX]{x1D739})$
is shown in figure 8(c), and confirms that the p.d.f. is concentrated at two diagonal locations in front of and behind the reference Q4. It is tempting to associate its downwards tilt with a systematic vertical meandering of the streaks, but the explanation is probably simpler. We have seen that small eddies are basically decoupled from the shear and the mean velocity. However, Q4s are defined by
$p^{44}(\unicode[STIX]{x1D739})$
is shown in figure 8(c), and confirms that the p.d.f. is concentrated at two diagonal locations in front of and behind the reference Q4. It is tempting to associate its downwards tilt with a systematic vertical meandering of the streaks, but the explanation is probably simpler. We have seen that small eddies are basically decoupled from the shear and the mean velocity. However, Q4s are defined by
![]() $u>0$
and
$u>0$
and
![]() $v<0$
, so that the flow velocity within them is tilted downwards, and we have seen in figure 8(a) that their separation suggests that they are pieces of larger structures whose connectivity is broken by weaker velocity fluctuations. It is then natural to expect from continuity that the closest Q of the same kind is located in the direction of the predominant velocity fluctuations which, in the case of Q4s, is the downwards diagonal. This is sketched by the nominal velocity arrows in figure 8(c), and confirmed by figure 8(d), which contains the relative position of Q1s. They are predominantly arranged along the upwards diagonal, corresponding to the mean velocity in a Q1. This is even more clearly shown by the lines with closed squares in figure 8(b,d), which correspond to small Q
$v<0$
, so that the flow velocity within them is tilted downwards, and we have seen in figure 8(a) that their separation suggests that they are pieces of larger structures whose connectivity is broken by weaker velocity fluctuations. It is then natural to expect from continuity that the closest Q of the same kind is located in the direction of the predominant velocity fluctuations which, in the case of Q4s, is the downwards diagonal. This is sketched by the nominal velocity arrows in figure 8(c), and confirmed by figure 8(d), which contains the relative position of Q1s. They are predominantly arranged along the upwards diagonal, corresponding to the mean velocity in a Q1. This is even more clearly shown by the lines with closed squares in figure 8(b,d), which correspond to small Q
![]() $_{uw}$
eddies in M32. Their separations agree well with those of the Q
$_{uw}$
eddies in M32. Their separations agree well with those of the Q
![]() $_{uv}$
, and their positions are aligned along their corresponding diagonals, although in the
$_{uv}$
, and their positions are aligned along their corresponding diagonals, although in the
![]() $(x,z)$
plane, rather than in
$(x,z)$
plane, rather than in
![]() $(x,y)$
.
$(x,y)$
.
The interpretation that neighbouring Qs of the same kind are fragments of larger structures is confirmed by the conditional velocity field in figure 8(e), which shows the streamwise velocity conditioned to the presence of a pair of Q4s, in terms of the similarity coordinate,
where
![]() $\boldsymbol{x}_{cog}$
is the position of the common centre of gravity of the Qs involved in the pair and
$\boldsymbol{x}_{cog}$
is the position of the common centre of gravity of the Qs involved in the pair and
![]() $d_{12}=(d_{1}+d_{2})/2$
is the mean of their diagonals
$d_{12}=(d_{1}+d_{2})/2$
is the mean of their diagonals
![]() $d_{j}$
. The two neighbours are seen to be enclosed within the same velocity structure.
$d_{j}$
. The two neighbours are seen to be enclosed within the same velocity structure.

Figure 9. Relative position of the closest Q4 to a given Q2: ▫, M32; ○, H32; ▵, C2000 with
![]() $y_{min}^{+}\geqslant 100$
. The solid squares are Q
$y_{min}^{+}\geqslant 100$
. The solid squares are Q
![]() $_{uw}$
in M32. (a) Average closest distance
$_{uw}$
in M32. (a) Average closest distance
![]() $\langle r^{(24)}\rangle$
, as a function of the diagonal of the reference Q2. The dashed line has slope
$\langle r^{(24)}\rangle$
, as a function of the diagonal of the reference Q2. The dashed line has slope
![]() $2/3$
. (b) Probability density function of
$2/3$
. (b) Probability density function of
![]() $r^{(24)}$
for different size bands centred at
$r^{(24)}$
for different size bands centred at
![]() $d^{(2)}/\unicode[STIX]{x1D702}=50,100,200,400$
, with the wider tails corresponding to the smaller structures. Case M32. Each p.d.f. is normalised with its mean value. The dashed line is the nearest-neighbour distribution for a Poisson point set in three-dimensional space. (c) Probability of ‘isolated’ Q2s, defined as those with no neighbour closer than
$d^{(2)}/\unicode[STIX]{x1D702}=50,100,200,400$
, with the wider tails corresponding to the smaller structures. Case M32. Each p.d.f. is normalised with its mean value. The dashed line is the nearest-neighbour distribution for a Poisson point set in three-dimensional space. (c) Probability of ‘isolated’ Q2s, defined as those with no neighbour closer than
![]() $r^{(24)}=2d^{(2)}$
, as a function of the diagonal of the reference Q2. (d) Anisotropy of the position of the closest Q4 with respect to a given Q2, as a function of
$r^{(24)}=2d^{(2)}$
, as a function of the diagonal of the reference Q2. (d) Anisotropy of the position of the closest Q4 with respect to a given Q2, as a function of
![]() $d^{(2)}$
.
$d^{(2)}$
.
5.2 Relative positions of structures of different kind
Figure 9(a) displays the mean distance between Qs of different kind (from a reference Q2 to its closest Q4). It contains the same viscous range as in the previous case,
![]() $d\lesssim 50\unicode[STIX]{x1D702}$
, but the distance between these Kolmogorov structures scales with the Taylor microscale
$d\lesssim 50\unicode[STIX]{x1D702}$
, but the distance between these Kolmogorov structures scales with the Taylor microscale
![]() $r^{(24)}\approx 3\unicode[STIX]{x1D706}$
. In addition, the inertial range is not self-similar any more, with
$r^{(24)}\approx 3\unicode[STIX]{x1D706}$
. In addition, the inertial range is not self-similar any more, with
![]() $r^{(24)}\sim d^{(0.5{-}0.7)}$
. Both issues are presumably related and, although they might admit dynamical explanations such as those given in § 4.3 for the intrinsic dimensions of the Qs, the reason is again probably simpler and geometrical. It follows from the distribution of the volume of the Qs given in § 3,
$r^{(24)}\sim d^{(0.5{-}0.7)}$
. Both issues are presumably related and, although they might admit dynamical explanations such as those given in § 4.3 for the intrinsic dimensions of the Qs, the reason is again probably simpler and geometrical. It follows from the distribution of the volume of the Qs given in § 3,
![]() $p(V)\sim V^{-5/3}$
, that the probability distribution of
$p(V)\sim V^{-5/3}$
, that the probability distribution of
![]() $d\sim V^{1/3}$
is
$d\sim V^{1/3}$
is
![]() $p(d)=p(V)\,(\,\text{d}V/\,\text{d}d)\sim d^{-\unicode[STIX]{x1D6FD}}$
, with
$p(d)=p(V)\,(\,\text{d}V/\,\text{d}d)\sim d^{-\unicode[STIX]{x1D6FD}}$
, with
![]() $\unicode[STIX]{x1D6FD}=3$
. In practice, the exponent ranges from
$\unicode[STIX]{x1D6FD}=3$
. In practice, the exponent ranges from
![]() $\unicode[STIX]{x1D6FD}=2.8$
for L38 to
$\unicode[STIX]{x1D6FD}=2.8$
for L38 to
![]() $\unicode[STIX]{x1D6FD}=3.3$
for H32 and
$\unicode[STIX]{x1D6FD}=3.3$
for H32 and
![]() $\unicode[STIX]{x1D6FD}=4$
for C2000. When looking for nearest neighbours satisfying condition (5.2), the number of available candidates per unit volume is then proportional to
$\unicode[STIX]{x1D6FD}=4$
for C2000. When looking for nearest neighbours satisfying condition (5.2), the number of available candidates per unit volume is then proportional to
where
![]() $d$
without a sub- or super-index should be understood as applying to the reference structure in a pair. Because of the restriction (5.2), such
$d$
without a sub- or super-index should be understood as applying to the reference structure in a pair. Because of the restriction (5.2), such
![]() $d$
is also proportional to the average diameter of the two structures being considered. Assuming a statistically uniform spatial distribution of the candidate structures, the average distance from a randomly chosen point to the closest structure is
$d$
is also proportional to the average diameter of the two structures being considered. Assuming a statistically uniform spatial distribution of the candidate structures, the average distance from a randomly chosen point to the closest structure is
![]() $\langle r^{(ij)}\rangle \sim n^{-1/3}\sim d^{(\unicode[STIX]{x1D6FD}-1)/3}$
. The dashed line in figure 9(a) is drawn with slope
$\langle r^{(ij)}\rangle \sim n^{-1/3}\sim d^{(\unicode[STIX]{x1D6FD}-1)/3}$
. The dashed line in figure 9(a) is drawn with slope
![]() $2/3\;(\unicode[STIX]{x1D6FD}=3)$
. It represents the data well, although the slope increase from M32 to C2000 (corresponding to an increase in
$2/3\;(\unicode[STIX]{x1D6FD}=3)$
. It represents the data well, although the slope increase from M32 to C2000 (corresponding to an increase in
![]() $\unicode[STIX]{x1D6FD}$
) is clear. In particular, it should be noted that
$\unicode[STIX]{x1D6FD}$
) is clear. In particular, it should be noted that
![]() $\unicode[STIX]{x1D6FD}=4$
results in
$\unicode[STIX]{x1D6FD}=4$
results in
![]() $\langle r\rangle \sim d$
, which agrees with the steeper slope of C2000 in figure 9(a), and with the results in LFJ12. This dependence also explains the scaling of the minimum distance with
$\langle r\rangle \sim d$
, which agrees with the steeper slope of C2000 in figure 9(a), and with the results in LFJ12. This dependence also explains the scaling of the minimum distance with
![]() $\unicode[STIX]{x1D706}$
. Invoking the independence of the large scales of turbulence with respect to the Reynolds number, which requires that structures with
$\unicode[STIX]{x1D706}$
. Invoking the independence of the large scales of turbulence with respect to the Reynolds number, which requires that structures with
![]() $d=O(L_{c})$
should be separated by distances
$d=O(L_{c})$
should be separated by distances
![]() $r=O(L_{c})$
, the previous relation should be written as
$r=O(L_{c})$
, the previous relation should be written as
Substituting
![]() $d\sim O(\unicode[STIX]{x1D702})$
in this equation, we obtain
$d\sim O(\unicode[STIX]{x1D702})$
in this equation, we obtain
![]() $r\sim O(\unicode[STIX]{x1D706})Re_{\unicode[STIX]{x1D706}}^{(3-\unicode[STIX]{x1D6FD})/2}$
, which is very close to
$r\sim O(\unicode[STIX]{x1D706})Re_{\unicode[STIX]{x1D706}}^{(3-\unicode[STIX]{x1D6FD})/2}$
, which is very close to
![]() $\unicode[STIX]{x1D706}$
when
$\unicode[STIX]{x1D706}$
when
![]() $\unicode[STIX]{x1D6FD}\approx 3$
.
$\unicode[STIX]{x1D6FD}\approx 3$
.
The rest of figure 9 tests this model. Figure 9(b) displays the p.d.f.s of the distance among Q4s and Q2s for different bands of sizes of the reference structure in the ‘inertial’ range,
![]() $50\unicode[STIX]{x1D702}<d^{(2)}<4L_{c}$
, each of them normalised by their mean separation. They are compared with the distribution of closest distances for a Poisson point set in which the average number of points within a sphere of radius
$50\unicode[STIX]{x1D702}<d^{(2)}<4L_{c}$
, each of them normalised by their mean separation. They are compared with the distribution of closest distances for a Poisson point set in which the average number of points within a sphere of radius
![]() $r$
is
$r$
is
![]() $N(r)=(r/R)^{3}$
. This distribution can be computed as the derivative with respect to
$N(r)=(r/R)^{3}$
. This distribution can be computed as the derivative with respect to
![]() $r$
of the probability of finding no points closer than
$r$
of the probability of finding no points closer than
![]() $r$
(Feller Reference Feller1971),
$r$
(Feller Reference Feller1971),
The parameter
![]() $R$
is related both to the average point density per unit volume,
$R$
is related both to the average point density per unit volume,
![]() $n=3/4\unicode[STIX]{x03C0}R^{3}$
, and to the average distance to the nearest neighbour,
$n=3/4\unicode[STIX]{x03C0}R^{3}$
, and to the average distance to the nearest neighbour,
![]() $\langle r\rangle \approx 0.89R$
. The different p.d.f.s agree reasonably well among themselves and with the Poisson model.
$\langle r\rangle \approx 0.89R$
. The different p.d.f.s agree reasonably well among themselves and with the Poisson model.
It was found by LFJ12 that tall attached Q2s in channels tend to be associated with similar Q4s within a distance of
![]() $O(d)$
, and that such pairs behave like coherent flow units that organise the flow between the pair into a quasi-streamwise ‘roller’. Structures that are much farther apart should be considered as isolated, and are unlikely to influence each other. A consequence of the two previous figures is that the average separation between small Qs of different kind tends to be much larger than their size, so that most of them cannot be considered to form part of a pair. Figure 9(c) shows the probability that a Q2 is isolated in the sense that its closest Q4 is at
$O(d)$
, and that such pairs behave like coherent flow units that organise the flow between the pair into a quasi-streamwise ‘roller’. Structures that are much farther apart should be considered as isolated, and are unlikely to influence each other. A consequence of the two previous figures is that the average separation between small Qs of different kind tends to be much larger than their size, so that most of them cannot be considered to form part of a pair. Figure 9(c) shows the probability that a Q2 is isolated in the sense that its closest Q4 is at
![]() $r^{(24)}>\unicode[STIX]{x1D6FC}_{d}d^{(2)}$
, with
$r^{(24)}>\unicode[STIX]{x1D6FC}_{d}d^{(2)}$
, with
![]() $\unicode[STIX]{x1D6FC}_{d}=2$
. It shows that Qs smaller than
$\unicode[STIX]{x1D6FC}_{d}=2$
. It shows that Qs smaller than
![]() $d/\unicode[STIX]{x1D706}\approx 5$
are most likely isolated, but that larger ones are not. The same holds for detached Qs in channels. Several scalings of
$d/\unicode[STIX]{x1D706}\approx 5$
are most likely isolated, but that larger ones are not. The same holds for detached Qs in channels. Several scalings of
![]() $d$
were tested for figure 9(c), and the one with
$d$
were tested for figure 9(c), and the one with
![]() $\unicode[STIX]{x1D706}$
works best for this particular choice of
$\unicode[STIX]{x1D706}$
works best for this particular choice of
![]() $\unicode[STIX]{x1D6FC}_{d}$
. This is not very surprising, because we have seen that the smallest distance between different kinds of Qs is also
$\unicode[STIX]{x1D6FC}_{d}$
. This is not very surprising, because we have seen that the smallest distance between different kinds of Qs is also
![]() $O(\unicode[STIX]{x1D706})$
, but it is inconsistent with (5.5), which implies that
$O(\unicode[STIX]{x1D706})$
, but it is inconsistent with (5.5), which implies that
![]() $r\sim d$
when
$r\sim d$
when
![]() $r\sim L_{c}$
. Changing the multiple
$r\sim L_{c}$
. Changing the multiple
![]() $\unicode[STIX]{x1D6FC}_{d}$
used to define isolated structures moves the curves in figure 9(c) to the right or left, and also changes their scaling slightly. The choice above,
$\unicode[STIX]{x1D6FC}_{d}$
used to define isolated structures moves the curves in figure 9(c) to the right or left, and also changes their scaling slightly. The choice above,
![]() $\unicode[STIX]{x1D6FC}_{d}=2$
, was selected for consistency with the scaling in figure 9(d), which is independent of
$\unicode[STIX]{x1D6FC}_{d}=2$
, was selected for consistency with the scaling in figure 9(d), which is independent of
![]() $\unicode[STIX]{x1D6FC}_{d}$
, but we will see later that
$\unicode[STIX]{x1D6FC}_{d}$
, but we will see later that
![]() $\unicode[STIX]{x1D6FC}_{d}=1$
leads to sharper conditional flow fields for pairs of structures.
$\unicode[STIX]{x1D6FC}_{d}=1$
leads to sharper conditional flow fields for pairs of structures.
In fact, most of the rest of this section could be written substituting
![]() $\unicode[STIX]{x1D706}^{1/3}$
for
$\unicode[STIX]{x1D706}^{1/3}$
for
![]() $L_{c}^{1/3}$
in (5.5). The available range of Reynolds numbers is not sufficient to distinguish the
$L_{c}^{1/3}$
in (5.5). The available range of Reynolds numbers is not sufficient to distinguish the
![]() $Re_{\unicode[STIX]{x1D706}}^{1/3}$
factor between the two scalings, which only changes by
$Re_{\unicode[STIX]{x1D706}}^{1/3}$
factor between the two scalings, which only changes by
![]() $1.3$
among the cases in figure 9. It can be shown that the
$1.3$
among the cases in figure 9. It can be shown that the
![]() $r\sim d^{2/3}$
law ceases to hold for
$r\sim d^{2/3}$
law ceases to hold for
![]() $d^{(2)}\gtrsim 5L_{c}$
, above which limit the mean distance is
$d^{(2)}\gtrsim 5L_{c}$
, above which limit the mean distance is
![]() $r/L_{c}=5{-}10$
for all Reynolds numbers. This limit corresponds to
$r/L_{c}=5{-}10$
for all Reynolds numbers. This limit corresponds to
![]() $10\unicode[STIX]{x1D706}$
in M32 and
$10\unicode[STIX]{x1D706}$
in M32 and
![]() $20\unicode[STIX]{x1D706}$
in H32, which are not far from where the structures become paired in figure 9(c). In fact, it can be argued that only H32 has a convincing 2/3 range in figure 9(a). From now on, in the absence of data over a wider range of Reynolds number, we plot each figure in the scaling that works best for it, without paying too much attention to mutual consistency.
$20\unicode[STIX]{x1D706}$
in H32, which are not far from where the structures become paired in figure 9(c). In fact, it can be argued that only H32 has a convincing 2/3 range in figure 9(a). From now on, in the absence of data over a wider range of Reynolds number, we plot each figure in the scaling that works best for it, without paying too much attention to mutual consistency.
Finally, figure 9(d) tests the preferential orientation of the location of Q4s with respect to the reference Q2. The Poisson model suggests that mutually isolated structures should be isotropically distributed with respect to each other, while only those that form pairs would be organised in particular ways (LFJ12). A position-anisotropy tensor can be defined as
![]() $\unicode[STIX]{x1D70C}_{ij}=\langle r_{i}r_{j}\rangle /\langle r_{k}r_{k}\rangle -\unicode[STIX]{x1D6FF}_{ij}/3$
, where
$\unicode[STIX]{x1D70C}_{ij}=\langle r_{i}r_{j}\rangle /\langle r_{k}r_{k}\rangle -\unicode[STIX]{x1D6FF}_{ij}/3$
, where
![]() $\boldsymbol{r}$
is the relative position vector between two structures. The anisotropy of the relative positions can be measured by the second invariant
$\boldsymbol{r}$
is the relative position vector between two structures. The anisotropy of the relative positions can be measured by the second invariant
![]() $\unicode[STIX]{x1D701}_{rr}^{2}=\unicode[STIX]{x1D70C}_{ij}\unicode[STIX]{x1D70C}_{ji}/6$
of
$\unicode[STIX]{x1D701}_{rr}^{2}=\unicode[STIX]{x1D70C}_{ij}\unicode[STIX]{x1D70C}_{ji}/6$
of
![]() $\unicode[STIX]{x1D70C}_{ij}$
, defined in the same way as the Lumley invariant of the Reynolds-stress tensor. Although
$\unicode[STIX]{x1D70C}_{ij}$
, defined in the same way as the Lumley invariant of the Reynolds-stress tensor. Although
![]() $\unicode[STIX]{x1D701}_{rr}$
is only an incomplete measure of isotropy, figure 9(d) shows that small Qs are essentially isotropically distributed with respect to each other, as required by the Poisson model, but that the isotropy breaks down for sizes of the same order as those at which the structures begin to pair. The behaviour of channels is different in this respect, presumably because of the interference from the wall, and the preferential orientation begins for much smaller eddies that do not necessarily form pairs.
$\unicode[STIX]{x1D701}_{rr}$
is only an incomplete measure of isotropy, figure 9(d) shows that small Qs are essentially isotropically distributed with respect to each other, as required by the Poisson model, but that the isotropy breaks down for sizes of the same order as those at which the structures begin to pair. The behaviour of channels is different in this respect, presumably because of the interference from the wall, and the preferential orientation begins for much smaller eddies that do not necessarily form pairs.
It should be noted that these arguments do not apply to Qs of the same kind, where we have seen that neighbouring structures may be separated by relatively weak fluctuations that happen to cross the detection threshold. Candidate neighbours cannot then be assumed to be uniformly distributed. On the contrary, Qs of different kind are necessarily separated by velocity differences
![]() $O(u^{\prime })$
, and, if we restrict the magnitude of the velocity gradients to their average value,
$O(u^{\prime })$
, and, if we restrict the magnitude of the velocity gradients to their average value,
![]() $O(\unicode[STIX]{x1D714}^{\prime })$
, such velocity jumps are unlikely to occur across distances much smaller than
$O(\unicode[STIX]{x1D714}^{\prime })$
, such velocity jumps are unlikely to occur across distances much smaller than
![]() $\unicode[STIX]{x1D706}\sim u^{\prime }/\unicode[STIX]{x1D714}^{\prime }$
.
$\unicode[STIX]{x1D706}\sim u^{\prime }/\unicode[STIX]{x1D714}^{\prime }$
.

Figure 10. Cross-sections of the three-dimensional joint p.d.f. of the position of the closest Q4 relative to a given Q2: ▫, M32; ○, H32; ▵, C2000 with
![]() $y_{min}^{+}\geqslant 100$
. The similarity variable is defined in (5.7). The p.d.f.s are integrated over
$y_{min}^{+}\geqslant 100$
. The similarity variable is defined in (5.7). The p.d.f.s are integrated over
![]() $\unicode[STIX]{x1D707}=\pm 0.2$
normal to the plane of the plot, and symmetrised around
$\unicode[STIX]{x1D707}=\pm 0.2$
normal to the plane of the plot, and symmetrised around
![]() $\unicode[STIX]{x1D707}_{z}=0$
. (a) In the
$\unicode[STIX]{x1D707}_{z}=0$
. (a) In the
![]() $(z,x)$
plane, for small Q4s
$(z,x)$
plane, for small Q4s
![]() $(50\unicode[STIX]{x1D702}<d^{(2)}<2L_{c})$
. (b) In the diagonal plane orthogonal to
$(50\unicode[STIX]{x1D702}<d^{(2)}<2L_{c})$
. (b) In the diagonal plane orthogonal to
![]() $\boldsymbol{r}=[1,-1,0]$
, for small Q4s. The probability contours in (a,b) contain the highest 30 % of the data. (c) Three-dimensional
$\boldsymbol{r}=[1,-1,0]$
, for small Q4s. The probability contours in (a,b) contain the highest 30 % of the data. (c) Three-dimensional
![]() $p^{24}$
in M32 for
$p^{24}$
in M32 for
![]() $d<4L_{c}$
, as in (b). The black arrow at the centre of the box is the nominal velocity for a Q2. That at the right-hand end of the p.d.f. is a Q4, and opposes the central one, suggesting a mechanism by which the p.d.f. is excluded from the diagonal and concentrated at the equatorial plane. (d) As in (b) for H32: ——,
$d<4L_{c}$
, as in (b). The black arrow at the centre of the box is the nominal velocity for a Q2. That at the right-hand end of the p.d.f. is a Q4, and opposes the central one, suggesting a mechanism by which the p.d.f. is excluded from the diagonal and concentrated at the equatorial plane. (d) As in (b) for H32: ——,
![]() $50\unicode[STIX]{x1D702}<d^{(2)}<L_{c}/2$
; - - - -,
$50\unicode[STIX]{x1D702}<d^{(2)}<L_{c}/2$
; - - - -,
![]() $d^{(2)}>L_{c}$
. Contours contain 20 % and 40 % of the data.
$d^{(2)}>L_{c}$
. Contours contain 20 % and 40 % of the data.
Figure 10 displays sections of the three-dimensional p.d.f.s of the relative positions of Q4s with respect to a Q2. As in figure 8, statistics can only be compiled by scaling distances properly and, following (5.5), the similarity scaling (5.1) is substituted by
It should be noted that the same scale is used for all of the flows, even if figure 9(a) shows that their actual average distance is not exactly the same, especially for the channel. Figure 10(a), which displays the section of the p.d.f.s in the
![]() $(z,x)$
plane, shows that the three flows collapse well. The result is similar to that found by LFJ12 for attached Qs in channels. There is essentially no probability of finding a Q4 in front of or behind the Q2, and the closest Q4s are found in the spanwise direction. The symmetry of this p.d.f. is statistical. It was shown in LFJ12 that, when the direction of the closest partner is defined as positive, the groups are found to be pairs, not trios; i.e. the second-closest partner is either much farther away, missing or in the same direction as the closest one. The same was found to be true here.
$(z,x)$
plane, shows that the three flows collapse well. The result is similar to that found by LFJ12 for attached Qs in channels. There is essentially no probability of finding a Q4 in front of or behind the Q2, and the closest Q4s are found in the spanwise direction. The symmetry of this p.d.f. is statistical. It was shown in LFJ12 that, when the direction of the closest partner is defined as positive, the groups are found to be pairs, not trios; i.e. the second-closest partner is either much farther away, missing or in the same direction as the closest one. The same was found to be true here.
However, the Qs in figure 10(a) are relatively small
![]() $(d<2L_{c})$
, and arguments similar to the ones used in the previous section for
$(d<2L_{c})$
, and arguments similar to the ones used in the previous section for
![]() $\boldsymbol{r}^{(44)}$
suggest that some of the properties of the p.d.f. might be kinematic. Since the perturbation velocity in a Q2 is directed along the downwards streamwise diagonal,
$\boldsymbol{r}^{(44)}$
suggest that some of the properties of the p.d.f. might be kinematic. Since the perturbation velocity in a Q2 is directed along the downwards streamwise diagonal,
![]() $\boldsymbol{u}\sim [-1,1,0]$
, it tends to exclude from that direction structures with an opposing velocity (
$\boldsymbol{u}\sim [-1,1,0]$
, it tends to exclude from that direction structures with an opposing velocity (
![]() $\boldsymbol{u}\sim [1,-1,0]$
for a Q4). In fact, the p.d.f. of
$\boldsymbol{u}\sim [1,-1,0]$
for a Q4). In fact, the p.d.f. of
![]() $\boldsymbol{r}^{(24)}$
should be complementary to that for
$\boldsymbol{r}^{(24)}$
should be complementary to that for
![]() $\boldsymbol{r}^{(44)}$
: empty along the downwards sloping diagonal and concentrated on the equatorial plane normal to that direction. This turns out to be true. Figure 10(b) shows a section along this inclined equatorial plane and reveals that the two high-probability regions in figure 10(a) are sections of an inclined arch or semicircle, whose dimensions also collapse well among the different flows. The three-dimensional view in figure 10(c) shows that the fact that this equatorial section is not a full torus is not due to the misalignment of its plane. This figure also sketches the argument above about how conflicting axial velocities restrict where the p.d.f. can be expected to be located in the space of relative positions. Figure 10(d) shows the relative p.d.f.s of small and large Qs, and proves that the arch-like character is predominantly a property of large structures; small ones are distributed more isotropically in the equatorial plane. It should be emphasised again that the symmetry of the distributions in figure 10 is statistical, due to the symmetry S1 in § 4. In fact, this symmetry is explicitly enforced on the plot to improve statistics. It should also be made clear that these distributions do not represent the shape of any structure, even on the average. They describe probabilities of the relative positions of the centres of gravity of different structures of different kind.
$\boldsymbol{r}^{(44)}$
: empty along the downwards sloping diagonal and concentrated on the equatorial plane normal to that direction. This turns out to be true. Figure 10(b) shows a section along this inclined equatorial plane and reveals that the two high-probability regions in figure 10(a) are sections of an inclined arch or semicircle, whose dimensions also collapse well among the different flows. The three-dimensional view in figure 10(c) shows that the fact that this equatorial section is not a full torus is not due to the misalignment of its plane. This figure also sketches the argument above about how conflicting axial velocities restrict where the p.d.f. can be expected to be located in the space of relative positions. Figure 10(d) shows the relative p.d.f.s of small and large Qs, and proves that the arch-like character is predominantly a property of large structures; small ones are distributed more isotropically in the equatorial plane. It should be emphasised again that the symmetry of the distributions in figure 10 is statistical, due to the symmetry S1 in § 4. In fact, this symmetry is explicitly enforced on the plot to improve statistics. It should also be made clear that these distributions do not represent the shape of any structure, even on the average. They describe probabilities of the relative positions of the centres of gravity of different structures of different kind.
The arched p.d.f. in figure 10(c) is different from that between pairs of attached Qs in channels, and also different from the conditional distribution of close pairs of Qs of different kind shown later in § 6. In these two cases, the interaction between the structures in the pair is strong, and the predominant probability distribution is formed by a Q2 and a Q4 located spanwise from one another. The p.d.f.s in figure 10 are dominated by small structures that are typically far from each other, and represent the effect of the larger flow features containing them. The shape of the p.d.f. depends on the structures involved. It follows from symmetry that the arches in figure 10 become ‘Us’ for the position of Q2s relative to a Q4 in HST. The same is true for the detached Qs in channels. The interpretation of these shapes is interesting. The Q4s in figure 10 are structures of high streamwise velocity. The figure shows that they tend to be located above or to the side of the low-streamwise-velocity Q2s, but not below. The complementary shape of the p.d.f. of
![]() $\boldsymbol{r}^{(42)}$
carries the same message: high velocity is above low velocity in the presence of a Q
$\boldsymbol{r}^{(42)}$
carries the same message: high velocity is above low velocity in the presence of a Q
![]() $^{-}$
. This is the direction of the ambient shear, and, since the Qs are defined from perturbation velocities, the implication is that they tend to be located in regions in which the shear is higher than the mean. This is reasonable, since they have to draw their energy from the local velocity difference, and has been mentioned often in the context of vortical structures (see, for example, Adrian Reference Adrian2007). These high-shear regions can be interpreted as the sharp interfaces between relatively uniform streamwise-velocity streaks, which are known to be layers of high activity both in the buffer region (Kim, Moin & Moser Reference Kim, Moin and Moser1987; Jiménez & Pinelli Reference Jiménez and Pinelli1999; Schoppa & Hussain Reference Schoppa and Hussain2002) and in the logarithmic layer (Meinhart & Adrian Reference Meinhart and Adrian1995; Flores & Jiménez Reference Flores and Jiménez2006). In the buffer layer, the high shear close to the wall substitutes the horizontal segment of the arch in figure 10, and the attached Qs are only concentrated in the lateral boundaries between low- and high-velocity streaks (although see the enveloping high-velocity streak in figure 12d of LFJ12, and the conditional flow fields in the next section). What figure 10 implies is that, away from the wall or in HST, the Qs concentrate either on the side or on the top boundary of the low-velocity streaks. A little thought shows that it also implies that only the top part of the low-velocity streaks and the bottom part of the high-velocity ones are sharp. Both of them are co-shear layers. The bottom part of the low-velocity streaks and the top part of the high-velocity ones, which would require layers of counter-shear vorticity, are either not sharp or contain no Qs. A similar arrangement of zones of relatively uniform velocity bounded by sharp interfaces has been discussed often in the literature (e.g. Meinhart & Adrian Reference Meinhart and Adrian1995).
$^{-}$
. This is the direction of the ambient shear, and, since the Qs are defined from perturbation velocities, the implication is that they tend to be located in regions in which the shear is higher than the mean. This is reasonable, since they have to draw their energy from the local velocity difference, and has been mentioned often in the context of vortical structures (see, for example, Adrian Reference Adrian2007). These high-shear regions can be interpreted as the sharp interfaces between relatively uniform streamwise-velocity streaks, which are known to be layers of high activity both in the buffer region (Kim, Moin & Moser Reference Kim, Moin and Moser1987; Jiménez & Pinelli Reference Jiménez and Pinelli1999; Schoppa & Hussain Reference Schoppa and Hussain2002) and in the logarithmic layer (Meinhart & Adrian Reference Meinhart and Adrian1995; Flores & Jiménez Reference Flores and Jiménez2006). In the buffer layer, the high shear close to the wall substitutes the horizontal segment of the arch in figure 10, and the attached Qs are only concentrated in the lateral boundaries between low- and high-velocity streaks (although see the enveloping high-velocity streak in figure 12d of LFJ12, and the conditional flow fields in the next section). What figure 10 implies is that, away from the wall or in HST, the Qs concentrate either on the side or on the top boundary of the low-velocity streaks. A little thought shows that it also implies that only the top part of the low-velocity streaks and the bottom part of the high-velocity ones are sharp. Both of them are co-shear layers. The bottom part of the low-velocity streaks and the top part of the high-velocity ones, which would require layers of counter-shear vorticity, are either not sharp or contain no Qs. A similar arrangement of zones of relatively uniform velocity bounded by sharp interfaces has been discussed often in the literature (e.g. Meinhart & Adrian Reference Meinhart and Adrian1995).
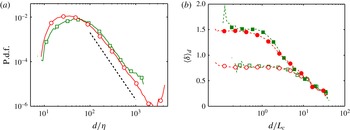
Figure 11. (a) Probability density function of the diagonal size of Q4s for which the nearest Q2 is at
![]() $r<d$
. The slope of the dashed line is
$r<d$
. The slope of the dashed line is
![]() $-3$
. (b) Mean dimensionless distance,
$-3$
. (b) Mean dimensionless distance,
![]() $\langle \unicode[STIX]{x1D6FF}\rangle _{d}$
, defined as in (5.3) for pairs in which the diameter of the reference object is
$\langle \unicode[STIX]{x1D6FF}\rangle _{d}$
, defined as in (5.3) for pairs in which the diameter of the reference object is
![]() $d$
. In both figures, ▫, M32; ○, H32. Solid symbols are for pairs with
$d$
. In both figures, ▫, M32; ○, H32. Solid symbols are for pairs with
![]() $r<2d$
and open ones are for
$r<2d$
and open ones are for
![]() $r<d$
. Only the latter case is plotted in (a) because the two cases are almost indistinguishable.
$r<d$
. Only the latter case is plotted in (a) because the two cases are almost indistinguishable.
6 Conditional flow fields
We present in this section conditional flow fields in the neighbourhood of paired structures of different kind, defined as being separated by
![]() $r\leqslant \unicode[STIX]{x1D6FC}_{d}d$
, with
$r\leqslant \unicode[STIX]{x1D6FC}_{d}d$
, with
![]() $\unicode[STIX]{x1D6FC}_{d}=1$
. A similar analysis was repeated for
$\unicode[STIX]{x1D6FC}_{d}=1$
. A similar analysis was repeated for
![]() $\unicode[STIX]{x1D6FC}_{d}=2$
, with little change, but the first choice results in somewhat sharper conditional fields, and was finally adopted. It should be noted that the results in the previous section do not preclude the existence of close pairs of arbitrarily small structures. In the case of structures of the same kind, the scaling
$\unicode[STIX]{x1D6FC}_{d}=2$
, with little change, but the first choice results in somewhat sharper conditional fields, and was finally adopted. It should be noted that the results in the previous section do not preclude the existence of close pairs of arbitrarily small structures. In the case of structures of the same kind, the scaling
![]() $\langle r\rangle \sim d$
guarantees that the fraction of paired structures is independent of their size, so that the statistics of the pairs are dominated by the more abundant small Qs (see figure 8
e). In the case of structures of different kind, the results in the previous section show that the fraction of isolated eddies increases with decreasing size, but, even so, it turns out that most of the paired structures are also small. We assume that the distribution of the distance between nearest neighbours follows the Poisson model (5.6). The probability of finding pairs among the population of Qs of size
$\langle r\rangle \sim d$
guarantees that the fraction of paired structures is independent of their size, so that the statistics of the pairs are dominated by the more abundant small Qs (see figure 8
e). In the case of structures of different kind, the results in the previous section show that the fraction of isolated eddies increases with decreasing size, but, even so, it turns out that most of the paired structures are also small. We assume that the distribution of the distance between nearest neighbours follows the Poisson model (5.6). The probability of finding pairs among the population of Qs of size
![]() $d$
would be
$d$
would be
Recalling that the mean distance between neighbours is
![]() $\langle r\rangle \sim R$
, and using the approximation in (5.5),
$\langle r\rangle \sim R$
, and using the approximation in (5.5),
![]() $\langle r\rangle \sim d^{(\unicode[STIX]{x1D6FD}-1)/3}$
, the argument of the exponential in (6.1) is proportional to
$\langle r\rangle \sim d^{(\unicode[STIX]{x1D6FD}-1)/3}$
, the argument of the exponential in (6.1) is proportional to
![]() $(d/L_{c})^{m}$
, with
$(d/L_{c})^{m}$
, with
![]() $m=4-\unicode[STIX]{x1D6FD}$
. The probability of finding close pairs among Qs of a given size then behaves as
$m=4-\unicode[STIX]{x1D6FD}$
. The probability of finding close pairs among Qs of a given size then behaves as
![]() $p_{2}\sim (d/L_{c})^{m}$
in the limit of small
$p_{2}\sim (d/L_{c})^{m}$
in the limit of small
![]() $d$
. Recalling that the probability of finding Qs of size
$d$
. Recalling that the probability of finding Qs of size
![]() $d$
decays like
$d$
decays like
![]() $d^{-\unicode[STIX]{x1D6FD}}$
, the expected number of pairs of size
$d^{-\unicode[STIX]{x1D6FD}}$
, the expected number of pairs of size
![]() $d$
behaves like
$d$
behaves like
![]() $n(d)\sim d^{-q}$
, with
$n(d)\sim d^{-q}$
, with
![]() $q=2\unicode[STIX]{x1D6FD}-4$
. For any
$q=2\unicode[STIX]{x1D6FD}-4$
. For any
![]() $\unicode[STIX]{x1D6FD}>2$
, this distribution is dominated by small structures, even if it remains true that most small structures are not involved in pairs. This is seen in the p.d.f.s of the number of near neighbours in figure 11(a), which is roughly consistent with
$\unicode[STIX]{x1D6FD}>2$
, this distribution is dominated by small structures, even if it remains true that most small structures are not involved in pairs. This is seen in the p.d.f.s of the number of near neighbours in figure 11(a), which is roughly consistent with
![]() $\unicode[STIX]{x1D6FD}=3\,(q=2)$
for
$\unicode[STIX]{x1D6FD}=3\,(q=2)$
for
![]() $d\gtrsim 50\unicode[STIX]{x1D702}$
.
$d\gtrsim 50\unicode[STIX]{x1D702}$
.
Figure 11(b) shows the mean dimensionless distance
![]() $\langle \unicode[STIX]{x1D6FF}\rangle _{d}$
between members of pairs in which the diameter of the reference object is
$\langle \unicode[STIX]{x1D6FF}\rangle _{d}$
between members of pairs in which the diameter of the reference object is
![]() $d$
. Corresponding to the definition of pairs as
$d$
. Corresponding to the definition of pairs as
![]() $r<\unicode[STIX]{x1D6FC}_{d}d$
, their mean spacing
$r<\unicode[STIX]{x1D6FC}_{d}d$
, their mean spacing
![]() $\langle r\rangle$
scales well with the eddy size
$\langle r\rangle$
scales well with the eddy size
![]() $d$
, at least for small Qs, and
$d$
, at least for small Qs, and
![]() $\langle \unicode[STIX]{x1D6FF}\rangle _{d}$
stays constant. The constricting effect of the box only becomes important when the eddies and their distances begin to be of the order of the integral length. The mean relative distance then decreases.
$\langle \unicode[STIX]{x1D6FF}\rangle _{d}$
stays constant. The constricting effect of the box only becomes important when the eddies and their distances begin to be of the order of the integral length. The mean relative distance then decreases.
In the remainder of this section, we discuss conditional flow fields compiled from structures in the ‘inertial’ range above
![]() $d\geqslant 50\unicode[STIX]{x1D702}$
(
$d\geqslant 50\unicode[STIX]{x1D702}$
(
![]() $d/L_{c}\geqslant 1.4$
for the HST case M32 used in most of the figures). It follows from the previous discussion that the correct scaling of the similarity variable is linear, as in (5.3) and LFJ12. We take advantage of the spanwise symmetry S1 to reorient flow fields so that the Q2 is on the left when facing along the flow. It then follows from the symmetry S3 of the HST that most conditional fields are either symmetric or antisymmetric with respect to
$d/L_{c}\geqslant 1.4$
for the HST case M32 used in most of the figures). It follows from the previous discussion that the correct scaling of the similarity variable is linear, as in (5.3) and LFJ12. We take advantage of the spanwise symmetry S1 to reorient flow fields so that the Q2 is on the left when facing along the flow. It then follows from the symmetry S3 of the HST that most conditional fields are either symmetric or antisymmetric with respect to
![]() $\unicode[STIX]{x1D739}=0$
. This is used to smooth statistics whenever appropriate.
$\unicode[STIX]{x1D739}=0$
. This is used to smooth statistics whenever appropriate.

Figure 12. Sections of the flow field conditioned to the presence of a Q2–Q4 pair. The condition includes all Qs with diagonals
![]() $d^{(2)}>50\unicode[STIX]{x1D702}$
whose centres of gravity are within
$d^{(2)}>50\unicode[STIX]{x1D702}$
whose centres of gravity are within
![]() $r^{(24)}\leqslant d^{(2)}$
. Homogeneous case M32. Coordinates as in (5.3), with the flow into the page. Pairs are oriented so that the Q2 is to the left when facing along the flow. The solid white contours are 0.7 of the maximum of the p.d.f. of the position of the points belonging to the Q
$r^{(24)}\leqslant d^{(2)}$
. Homogeneous case M32. Coordinates as in (5.3), with the flow into the page. Pairs are oriented so that the Q2 is to the left when facing along the flow. The solid white contours are 0.7 of the maximum of the p.d.f. of the position of the points belonging to the Q
![]() $^{-}$
s. The dashed ones are vortex clusters. The black line in each panel is the isosurface of the total streamwise velocity,
$^{-}$
s. The dashed ones are vortex clusters. The black line in each panel is the isosurface of the total streamwise velocity,
![]() $\{\widehat{u}\}$
, passing through the common centre of gravity of the Q pair. (a) Cross-section
$\{\widehat{u}\}$
, passing through the common centre of gravity of the Q pair. (a) Cross-section
![]() $(\unicode[STIX]{x1D6FF}_{x}=0)$
of the conditional perturbation velocity. Colours are
$(\unicode[STIX]{x1D6FF}_{x}=0)$
of the conditional perturbation velocity. Colours are
![]() $\{u\}^{+}\in [-1.35,1.35]$
, from blue to red (left to right). The longest arrows of the cross-flow conditional velocity field are
$\{u\}^{+}\in [-1.35,1.35]$
, from blue to red (left to right). The longest arrows of the cross-flow conditional velocity field are
![]() $0.95u_{\unicode[STIX]{x1D70F}}$
. (b) Cross-section
$0.95u_{\unicode[STIX]{x1D70F}}$
. (b) Cross-section
![]() $(\unicode[STIX]{x1D6FF}_{x}=0)$
of the conditional shear layer containing the pair in M32. The range is
$(\unicode[STIX]{x1D6FF}_{x}=0)$
of the conditional shear layer containing the pair in M32. The range is
![]() $\{\unicode[STIX]{x2202}_{y}\widehat{u}\}/S\in [0.3,2.5]$
. (c,d) As in (a,b) for detached Q
$\{\unicode[STIX]{x2202}_{y}\widehat{u}\}/S\in [0.3,2.5]$
. (c,d) As in (a,b) for detached Q
![]() $^{-}$
s in the channel C950 with
$^{-}$
s in the channel C950 with
![]() $d^{(2)}>50\unicode[STIX]{x1D702}$
,
$d^{(2)}>50\unicode[STIX]{x1D702}$
,
![]() $y_{cog}^{+}>100$
and
$y_{cog}^{+}>100$
and
![]() $y_{cog}/h<0.4$
. The ranges are
$y_{cog}/h<0.4$
. The ranges are
![]() $\{u\}^{+}\in [-1.3,1.5]$
and
$\{u\}^{+}\in [-1.3,1.5]$
and
![]() $\{\unicode[STIX]{x2202}_{y}\widehat{u}\}/S\in [0.05,3.1]$
.
$\{\unicode[STIX]{x2202}_{y}\widehat{u}\}/S\in [0.05,3.1]$
.
The similarity transformation (5.3) allows us to relate structures of different sizes, but its interpretation requires some care. Conditional averaging is defined at constant
![]() $\unicode[STIX]{x1D739}$
,
$\unicode[STIX]{x1D739}$
,
where
![]() $\boldsymbol{x}_{cog}$
and
$\boldsymbol{x}_{cog}$
and
![]() $d_{12}$
are defined in (5.3), but, since we saw above that the number of pairs decreases approximately as
$d_{12}$
are defined in (5.3), but, since we saw above that the number of pairs decreases approximately as
![]() $d^{-2}$
, the conditional fields are dominated by the smallest Qs in the sample.
$d^{-2}$
, the conditional fields are dominated by the smallest Qs in the sample.
A second caveat refers to the relation between conditional velocities and their gradients. Because different structures have different length scales, the relation
![]() $\{\unicode[STIX]{x2202}_{y}u\}=\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FF}}\{u\}$
is not even dimensionally correct. In fact, while conditional velocities have an absolute magnitude that can be expressed in wall units, their gradients in the conditional plane do not have a clear meaning, since they are averages of derivatives taken with respect to a wide range of scales. In this section, velocities and their gradients are averaged independently, and each of them has well-defined dimensions and units. However, some conditional quantities are not easy to relate back to the original fields. For example, the perturbation velocities in figure 12(a) are defined with respect to the local
$\{\unicode[STIX]{x2202}_{y}u\}=\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FF}}\{u\}$
is not even dimensionally correct. In fact, while conditional velocities have an absolute magnitude that can be expressed in wall units, their gradients in the conditional plane do not have a clear meaning, since they are averages of derivatives taken with respect to a wide range of scales. In this section, velocities and their gradients are averaged independently, and each of them has well-defined dimensions and units. However, some conditional quantities are not easy to relate back to the original fields. For example, the perturbation velocities in figure 12(a) are defined with respect to the local
![]() $U=Sy$
even if
$U=Sy$
even if
![]() $y$
has a different meaning for structures of different sizes. These conditional velocities only give a general sense of the geometry and intensity of individual eddies. On the other hand, the solid black curves in figure 12 represent the isocontour
$y$
has a different meaning for structures of different sizes. These conditional velocities only give a general sense of the geometry and intensity of individual eddies. On the other hand, the solid black curves in figure 12 represent the isocontour
![]() $\{\widehat{u}\}=Sy_{cog}$
of the total velocity. They give an idea of the streamwise-velocity streak containing the structures, but they do not coincide with
$\{\widehat{u}\}=Sy_{cog}$
of the total velocity. They give an idea of the streamwise-velocity streak containing the structures, but they do not coincide with
![]() $\{u\}=0$
.
$\{u\}=0$
.
Figure 12(a) displays the conditional velocity field in the cross-stream plane,
![]() $\unicode[STIX]{x1D6FF}_{x}=0$
. It should be compared with figure 12(d) in LFJ12, which is compiled for pairs of large attached eddies. There is a sweep sitting in a high-speed streak, paired with an ejection in a low-speed one. The vortex cluster sits between the two Qs. The main difference from LFJ12 is that the present pair is symmetric with respect to the origin, as required by the flow symmetries. Figure 12(b) shows that the Q pair sits in an inclined layer of high shear,
$\unicode[STIX]{x1D6FF}_{x}=0$
. It should be compared with figure 12(d) in LFJ12, which is compiled for pairs of large attached eddies. There is a sweep sitting in a high-speed streak, paired with an ejection in a low-speed one. The vortex cluster sits between the two Qs. The main difference from LFJ12 is that the present pair is symmetric with respect to the origin, as required by the flow symmetries. Figure 12(b) shows that the Q pair sits in an inclined layer of high shear,
![]() $\{\unicode[STIX]{x2202}_{y}\widehat{u}\}$
, which is up to 2.5 times stronger than the mean velocity gradient, as already deduced on different grounds at the end of § 5.2. The streaks themselves define relatively uniform regions in which the conditional shear is approximately one third of the ambient. The high-shear layer marks the boundary between the streaks.
$\{\unicode[STIX]{x2202}_{y}\widehat{u}\}$
, which is up to 2.5 times stronger than the mean velocity gradient, as already deduced on different grounds at the end of § 5.2. The streaks themselves define relatively uniform regions in which the conditional shear is approximately one third of the ambient. The high-shear layer marks the boundary between the streaks.
More comparable to the present case than the attached fields in LFJ12 are the conditional fields in figure 12(c,d), which are computed for the channel C950 using pairs of detached Q2–Q4 whose centre of gravity is in
![]() $y_{cog}^{+}\geqslant 100$
and
$y_{cog}^{+}\geqslant 100$
and
![]() $y_{cog}/h<0.4$
. Being far from the wall, these pairs are much more symmetric than the attached ones, but there is some residual asymmetry, visible in the difference between the two streaks, in the shape of the vortex cluster and in the non-uniform intensity of the shear layer.
$y_{cog}/h<0.4$
. Being far from the wall, these pairs are much more symmetric than the attached ones, but there is some residual asymmetry, visible in the difference between the two streaks, in the shape of the vortex cluster and in the non-uniform intensity of the shear layer.

Figure 13. Flow fields conditioned to the presence of a Q2–Q4 pair, as in figure 12, for the HST flow M32. (a) Cross-section
![]() $(\unicode[STIX]{x1D6FF}_{x}=0)$
of the conditional longitudinal ‘roller’ between the pair. The background is
$(\unicode[STIX]{x1D6FF}_{x}=0)$
of the conditional longitudinal ‘roller’ between the pair. The background is
![]() $\{\unicode[STIX]{x1D714}_{x}\}/\unicode[STIX]{x1D714}^{\prime }\in [-0.1,0.3]$
. (b) Streamwise section
$\{\unicode[STIX]{x1D714}_{x}\}/\unicode[STIX]{x1D714}^{\prime }\in [-0.1,0.3]$
. (b) Streamwise section
![]() $(\unicode[STIX]{x1D6FF}_{z}=0)$
of the conditional roller. The colours represent the magnitude of the conditional vorticity,
$(\unicode[STIX]{x1D6FF}_{z}=0)$
of the conditional roller. The colours represent the magnitude of the conditional vorticity,
![]() $|\{\unicode[STIX]{x1D74E}\}|/\unicode[STIX]{x1D714}^{\prime }\in [0,0.5]$
, and the arrows represent the conditional vorticity vector in the plane of the figure. The dashed diagonal is inclined at
$|\{\unicode[STIX]{x1D74E}\}|/\unicode[STIX]{x1D714}^{\prime }\in [0,0.5]$
, and the arrows represent the conditional vorticity vector in the plane of the figure. The dashed diagonal is inclined at
![]() $45^{\circ }$
. The single purple contour is the isoline of the conditional
$45^{\circ }$
. The single purple contour is the isoline of the conditional
![]() $\{\unicode[STIX]{x1D714}_{x}\}$
, at 0.5 of its maximum. (c) Three-dimensional p.d.f. of the position of the points belonging to the Q2 (green, left), Q4 (blue, right) and vortex cluster (grey, centre). Isosurfaces are 0.7 of the maximum of each p.d.f. (d) Three-dimensional p.d.f. of the points of the vortex cluster in (c) compared with the
$\{\unicode[STIX]{x1D714}_{x}\}$
, at 0.5 of its maximum. (c) Three-dimensional p.d.f. of the position of the points belonging to the Q2 (green, left), Q4 (blue, right) and vortex cluster (grey, centre). Isosurfaces are 0.7 of the maximum of each p.d.f. (d) Three-dimensional p.d.f. of the points of the vortex cluster in (c) compared with the
![]() $\{\unicode[STIX]{x2202}_{y}\widehat{u}\}/S=2.25$
isosurface of the conditional shear layer in figure 12(b). The flow in (c,d) is from the lower-left to the upper-right corner.
$\{\unicode[STIX]{x2202}_{y}\widehat{u}\}/S=2.25$
isosurface of the conditional shear layer in figure 12(b). The flow in (c,d) is from the lower-left to the upper-right corner.
Figure 13(a) shows the ‘roller’ between the two Qs, which is defined in this transverse plane by the conditional streamwise vorticity
![]() $\{\unicode[STIX]{x1D714}_{x}\}$
. This coherent vortex is fairly strong, even when compared with the background incoherent vorticity, but it should be noted that, although it is roughly at the same location as the vortex cluster, it does not coincide with it. The vortex cluster contains strong vorticity magnitudes,
$\{\unicode[STIX]{x1D714}_{x}\}$
. This coherent vortex is fairly strong, even when compared with the background incoherent vorticity, but it should be noted that, although it is roughly at the same location as the vortex cluster, it does not coincide with it. The vortex cluster contains strong vorticity magnitudes,
![]() $\{|\unicode[STIX]{x1D74E}|\}$
, without implying any particular orientation. The conditional roller represents coherent vorticity,
$\{|\unicode[STIX]{x1D74E}|\}$
, without implying any particular orientation. The conditional roller represents coherent vorticity,
![]() $|\{\unicode[STIX]{x1D74E}\}|$
, which can loosely be interpreted as the curl of the conditional velocity field of the ejection–sweep pair. The vortex cluster is characterised by the disorganised approximately isotropic vortices in figure 3(b), each of which has radius
$|\{\unicode[STIX]{x1D74E}\}|$
, which can loosely be interpreted as the curl of the conditional velocity field of the ejection–sweep pair. The vortex cluster is characterised by the disorganised approximately isotropic vortices in figure 3(b), each of which has radius
![]() $O(\unicode[STIX]{x1D702})$
(Jiménez et al.
Reference Jiménez, Wray, Saffman and Rogallo1993; del Álamo et al. Reference del Álamo, Jiménez, Zandonade and Moser2006). It was shown in Jiménez (Reference Jiménez2013b
) that the anisotropy of the orientation tensor of the vorticity of the fully resolved flow is proportional to
$O(\unicode[STIX]{x1D702})$
(Jiménez et al.
Reference Jiménez, Wray, Saffman and Rogallo1993; del Álamo et al. Reference del Álamo, Jiménez, Zandonade and Moser2006). It was shown in Jiménez (Reference Jiménez2013b
) that the anisotropy of the orientation tensor of the vorticity of the fully resolved flow is proportional to
![]() $S/\unicode[STIX]{x1D714}^{\prime }\sim Re_{\unicode[STIX]{x1D706}}^{-1}$
(SDJ16). The roller only survives conditional averaging because of this residual anisotropy. Rollers are large-scale structures whose radius is of the order of the separation of the pair of Qs, and each of them typically contains many individual small-scale vortices. If we assume that
$S/\unicode[STIX]{x1D714}^{\prime }\sim Re_{\unicode[STIX]{x1D706}}^{-1}$
(SDJ16). The roller only survives conditional averaging because of this residual anisotropy. Rollers are large-scale structures whose radius is of the order of the separation of the pair of Qs, and each of them typically contains many individual small-scale vortices. If we assume that
![]() $\{|\unicode[STIX]{x1D74E}|\}\approx \unicode[STIX]{x1D714}^{\prime }$
, and that the surviving conditional vorticity fraction is of the order of the anisotropy,
$\{|\unicode[STIX]{x1D74E}|\}\approx \unicode[STIX]{x1D714}^{\prime }$
, and that the surviving conditional vorticity fraction is of the order of the anisotropy,
![]() $|\{\unicode[STIX]{x1D74E}\}|/\{|\unicode[STIX]{x1D74E}|\}\approx S/\unicode[STIX]{x1D714}^{\prime }$
, it follows that we can at most expect conditional vorticities
$|\{\unicode[STIX]{x1D74E}\}|/\{|\unicode[STIX]{x1D74E}|\}\approx S/\unicode[STIX]{x1D714}^{\prime }$
, it follows that we can at most expect conditional vorticities
![]() $|\{\unicode[STIX]{x1D74E}\}|/S=O(1)$
, independently of the Reynolds number. In the present HST cases,
$|\{\unicode[STIX]{x1D74E}\}|/S=O(1)$
, independently of the Reynolds number. In the present HST cases,
![]() $Re_{\unicode[STIX]{x1D706}}=100{-}250$
,
$Re_{\unicode[STIX]{x1D706}}=100{-}250$
,
![]() $S/\unicode[STIX]{x1D714}^{\prime }=0.1{-}0.04$
(see table 2) and
$S/\unicode[STIX]{x1D714}^{\prime }=0.1{-}0.04$
(see table 2) and
![]() $|\{\unicode[STIX]{x1D74E}\}|/S\approx 5$
for Q pairs with
$|\{\unicode[STIX]{x1D74E}\}|/S\approx 5$
for Q pairs with
![]() $d\geqslant L_{c}$
. It should be noted that, because of the limited resolution of most imaging experiments, the ‘vortices’ observed in them probably represent these coarse-grained eddies, rather than individual structures of the true vorticity.
$d\geqslant L_{c}$
. It should be noted that, because of the limited resolution of most imaging experiments, the ‘vortices’ observed in them probably represent these coarse-grained eddies, rather than individual structures of the true vorticity.

Figure 14. (a–c) Effect of the inhomogeneity of the mean flow on the
![]() $\unicode[STIX]{x1D6FF}_{x}=0$
two-dimensional sections of the streamwise-velocity field conditioned to Q2–Q4 pairs. The flow and graphics are as in figure 12. The horizontal dashed lines pass through the average
$\unicode[STIX]{x1D6FF}_{x}=0$
two-dimensional sections of the streamwise-velocity field conditioned to Q2–Q4 pairs. The flow and graphics are as in figure 12. The horizontal dashed lines pass through the average
![]() $y_{cog}$
. (a) Homogeneous flow M32, as in figure 12(a). Velocity range
$y_{cog}$
. (a) Homogeneous flow M32, as in figure 12(a). Velocity range
![]() $\{u\}^{+}\in [-0.9,1.3]$
. (b) Detached Qs in the channel C950, as in figure 12(c). Velocity range
$\{u\}^{+}\in [-0.9,1.3]$
. (b) Detached Qs in the channel C950, as in figure 12(c). Velocity range
![]() $\{u\}^{+}\in [-1.3,1.5]$
. The similarity variables in (a,b) are as in (5.3). (c) Attached Qs in C950 for which
$\{u\}^{+}\in [-1.3,1.5]$
. The similarity variables in (a,b) are as in (5.3). (c) Attached Qs in C950 for which
![]() $y_{max}^{+}>100$
and
$y_{max}^{+}>100$
and
![]() $y_{max}/h<0.4$
. Velocity range
$y_{max}/h<0.4$
. Velocity range
![]() $\{u\}^{+}\in [-0.9,1.3]$
. The coordinates in this figure are normalised with the mean distance from the wall,
$\{u\}^{+}\in [-0.9,1.3]$
. The coordinates in this figure are normalised with the mean distance from the wall,
![]() $\unicode[STIX]{x1D739}^{\prime }=\boldsymbol{x}/(1.25y_{cog})$
, instead of with
$\unicode[STIX]{x1D739}^{\prime }=\boldsymbol{x}/(1.25y_{cog})$
, instead of with
![]() $d_{12}$
, so that the wall is at
$d_{12}$
, so that the wall is at
![]() $\unicode[STIX]{x1D6FF}_{y}^{\prime }=0$
. The prefactor of
$\unicode[STIX]{x1D6FF}_{y}^{\prime }=0$
. The prefactor of
![]() $y_{cog}$
is empirically chosen to give the same dimensionless distance between Qs as in (a,b). (d–f) Flows as in (a–c). The central opaque S-shaped object is the isosurface of the magnitude of the conditional perturbation vorticity,
$y_{cog}$
is empirically chosen to give the same dimensionless distance between Qs as in (a,b). (d–f) Flows as in (a–c). The central opaque S-shaped object is the isosurface of the magnitude of the conditional perturbation vorticity,
![]() $|\{\unicode[STIX]{x1D74E}\}|=0.25|\{\unicode[STIX]{x1D74E}\}|_{max}$
. The two translucent objects are isosurfaces of the conditional perturbation streamwise velocity,
$|\{\unicode[STIX]{x1D74E}\}|=0.25|\{\unicode[STIX]{x1D74E}\}|_{max}$
. The two translucent objects are isosurfaces of the conditional perturbation streamwise velocity,
![]() $\{u\}^{+}=\pm 0.6$
, as marked in (d).
$\{u\}^{+}=\pm 0.6$
, as marked in (d).
Neither the vortex cluster nor the roller coincides with the conditional shear layer, which is predominantly
![]() $\{\unicode[STIX]{x1D714}_{z}\}$
. Figure 13(b) shows that the roller is inclined at roughly
$\{\unicode[STIX]{x1D714}_{z}\}$
. Figure 13(b) shows that the roller is inclined at roughly
![]() $45^{\circ }$
to the streamwise direction, and that the conditional vorticity vector in this plane is inclined at roughly the same angle. The coloured background in figure 13(b) corresponds to the magnitude of this inclined conditional vorticity, but the single coloured contour of
$45^{\circ }$
to the streamwise direction, and that the conditional vorticity vector in this plane is inclined at roughly the same angle. The coloured background in figure 13(b) corresponds to the magnitude of this inclined conditional vorticity, but the single coloured contour of
![]() $\{\unicode[STIX]{x1D714}_{x}\}$
included in the figure shows that the conditional streamwise vorticity (and in fact all of the individual vorticity components) shares the geometry of the full conditional vorticity vector, at least in this central plane. It can also be shown that the inclination of the conditional roller with respect to the streamwise direction changes with the flow inhomogeneity (see also figure 14 below). For the detached pairs used in figure 12(c,d), the inclination of the roller is only
$\{\unicode[STIX]{x1D714}_{x}\}$
included in the figure shows that the conditional streamwise vorticity (and in fact all of the individual vorticity components) shares the geometry of the full conditional vorticity vector, at least in this central plane. It can also be shown that the inclination of the conditional roller with respect to the streamwise direction changes with the flow inhomogeneity (see also figure 14 below). For the detached pairs used in figure 12(c,d), the inclination of the roller is only
![]() $20^{\circ }$
to the horizontal, and for attached Q pairs the roller is almost aligned streamwise, as in the attached conditional structures in figure 12 of LFJ12. In all of these cases, the inclination of the conditional vorticity vector is roughly
$20^{\circ }$
to the horizontal, and for attached Q pairs the roller is almost aligned streamwise, as in the attached conditional structures in figure 12 of LFJ12. In all of these cases, the inclination of the conditional vorticity vector is roughly
![]() $45^{\circ }$
, independently of the shape and inclination of the region in which the vorticity is strong.
$45^{\circ }$
, independently of the shape and inclination of the region in which the vorticity is strong.
A three-dimensional representation of the relative positions and dimensions of the components of the pair is shown in figure 13(c). Its main difference from the attached eddies in LFJ12 is that the HST structures are roughly isotropic, instead of elongated, as already mentioned for detached Qs in LFJ12, and discussed in some detail in § 4.4. The relation between the vortex cluster and the host high-shear layer is shown in figure 13(d), which shows that the latter is inclined spanwise, marking the boundary between the high- and the low-speed streaks.
6.1 The effect of inhomogeneity in channels
Finally, figure 14 compares the structure of the conditional flow fields for the three kinds of Q pairs discussed in this paper. Figure 14(a–c) compares the field of the streamwise velocity in the cross-flow sections. It reveals the increasing effect of inhomogeneity as we move from HST in figure 14(a), to detached channel Q pairs in figure 14(b) and to attached Q pairs in figure 14(c). Figure 14(a,b) is the same as figure 12(a,c), but the three figures have now been scaled to have a similar distance between the average positions of the members of the pairs, and aligned to the same location of their centre of gravity. The main difference between detached channel pairs and HST is that the sweep gets larger than the ejection, presumably because it is coming from layers in which the integral length (proportional to
![]() $y$
) is larger. This difference gets most marked for the attached pairs in figure 14(c), where the high-speed streak of the sweep is considerably larger than the low-speed one (see also LFJ12). Comparing this figure with figure 14(a), it can almost be interpreted that the ejection is truncated by the presence of the impermeable wall. Although not shown in the figure, the high-shear layer of the attached pair is only clearly present above the low-velocity ejection streak. The layer underneath the high-velocity sweep has been absorbed by the high-shear viscous region at the wall. Otherwise, the differences between the three types of structures are relatively minor. In particular, the intensity of the conditional streaks is almost the same in the three cases.
$y$
) is larger. This difference gets most marked for the attached pairs in figure 14(c), where the high-speed streak of the sweep is considerably larger than the low-speed one (see also LFJ12). Comparing this figure with figure 14(a), it can almost be interpreted that the ejection is truncated by the presence of the impermeable wall. Although not shown in the figure, the high-shear layer of the attached pair is only clearly present above the low-velocity ejection streak. The layer underneath the high-velocity sweep has been absorbed by the high-shear viscous region at the wall. Otherwise, the differences between the three types of structures are relatively minor. In particular, the intensity of the conditional streaks is almost the same in the three cases.
Figure 14(d–f) shows three-dimensional views of the inclined roller mentioned in figure 13(a,b), now shown in relation to the high- and low-velocity streaks. Figure 14(d) reveals that the roller in HST is part of a conditional double ‘hairpin’, containing both an upright and an inverted hook, although it is important to remember that this is a conditional flow structure unlikely to represent any individual flow realisation, and that the roller is formed by the superposition of many small-scale vortices, each of which is almost isotropically oriented. Figure 14(d) shows that this double hairpin straddles both the high- and low-speed streaks in the background of figure 14(a,b), and it is interesting that both streaks extend ‘downstream’ from their respective hairpin end. The high-speed streak starts roughly at the inverted hairpin hook and extends to the right of the figure, while the low-speed streak extends in the opposite direction, starting from the upright hook. It is clear from the figure that the two ‘hooks’ are the high-shear layers whose cross-section was described in figure 12(b) and in § 5.2 as being located respectively above and below the low- and high-velocity streaks. A trivial observation is that the hairpins shown here are not connected to the wall in the wall-less HST flow.
The symmetry of figure 14(d) is a direct consequence of the statistical symmetries of HST. Figure 14(e) presents the same view of the conditional detached Q pairs in the logarithmic layer of the channel. Although less symmetric than in figure 14(d), the two figures are similar enough to strongly suggest that the same mechanisms are at play in both cases. When the plot is drawn for the attached Qs of the channel, the conditional figure is dominated by a strong vorticity layer attached to the wall, defined in this case as
![]() $\unicode[STIX]{x1D6FF}_{y}^{\prime }=0$
. Once this layer is removed by truncating the domain (to
$\unicode[STIX]{x1D6FF}_{y}^{\prime }=0$
. Once this layer is removed by truncating the domain (to
![]() $\unicode[STIX]{x1D6FF}_{y}^{\prime }>0.15$
in figure 14
f), the roller reappears, although with a much shallower inclination with respect to the mean stream than in the case of Q pairs located farther from the wall. It can best be described as one of the quasi-streamwise vortices of the classical descriptions of the buffer layer (Robinson Reference Robinson1991), although all of the Q pairs in this figure are large
$\unicode[STIX]{x1D6FF}_{y}^{\prime }>0.15$
in figure 14
f), the roller reappears, although with a much shallower inclination with respect to the mean stream than in the case of Q pairs located farther from the wall. It can best be described as one of the quasi-streamwise vortices of the classical descriptions of the buffer layer (Robinson Reference Robinson1991), although all of the Q pairs in this figure are large
![]() $(y_{max}^{+}>100)$
. The present definition of the roller in terms of the magnitude of the conditional vorticity incorporates the wall-parallel shear layer that can be seen in figure 14(f), forming an arch above the low-velocity streak. This layer corresponds to the upright hairpin hook in figure 14(d,e). The asymmetry between the streaks, already clear in figure 14(e), is exaggerated here, with a very large high-speed streak accompanying a much smaller low-speed one, hidden in the plot by the upright hook of the conditional roller. This agrees with the picture of the same case in figure 12(c) of LFJ12. It should be noted that, even in the attached case, there is a residual inverted hook that appears as a small isolated structure to the right of figure 14(f), but which is connected to the rest of the roller by the high-vorticity wall layer that has been removed for clarity.
$(y_{max}^{+}>100)$
. The present definition of the roller in terms of the magnitude of the conditional vorticity incorporates the wall-parallel shear layer that can be seen in figure 14(f), forming an arch above the low-velocity streak. This layer corresponds to the upright hairpin hook in figure 14(d,e). The asymmetry between the streaks, already clear in figure 14(e), is exaggerated here, with a very large high-speed streak accompanying a much smaller low-speed one, hidden in the plot by the upright hook of the conditional roller. This agrees with the picture of the same case in figure 12(c) of LFJ12. It should be noted that, even in the attached case, there is a residual inverted hook that appears as a small isolated structure to the right of figure 14(f), but which is connected to the rest of the roller by the high-vorticity wall layer that has been removed for clarity.
7 Conclusions
We have studied the three-dimensional intense Reynolds-stress structures (Qs) and vortex clusters of statistically stationary HST at
![]() $Re_{\unicode[STIX]{x1D706}}=50{-}250$
, and compared them with those of turbulent channels in the same range of Reynolds numbers. The main conclusion is that the Qs and vortex clusters in HST are essentially symmetrised versions of the corresponding detached structures in channels, while the absence of walls and spatial homogeneity of HST allow us to separate which properties of the wall-bounded structures are associated with the wall, and which ones should be generic to other shear flows.
$Re_{\unicode[STIX]{x1D706}}=50{-}250$
, and compared them with those of turbulent channels in the same range of Reynolds numbers. The main conclusion is that the Qs and vortex clusters in HST are essentially symmetrised versions of the corresponding detached structures in channels, while the absence of walls and spatial homogeneity of HST allow us to separate which properties of the wall-bounded structures are associated with the wall, and which ones should be generic to other shear flows.
We show in § 4.1 that, both in channels and in HST, most of the tangential Reynolds stress is carried by sweeps and ejections (Q
![]() $^{-}$
s) larger than the Corrsin scale
$^{-}$
s) larger than the Corrsin scale
![]() $L_{c}$
, which are therefore able to couple with the shear. In channels, such large structures are typically attached to the wall, but the results in HST strongly suggest that wall attachment is a geometric consequence of their size, and not the reason for their dynamical relevance. Vortex clusters tend to be smaller, and to be associated with Q
$L_{c}$
, which are therefore able to couple with the shear. In channels, such large structures are typically attached to the wall, but the results in HST strongly suggest that wall attachment is a geometric consequence of their size, and not the reason for their dynamical relevance. Vortex clusters tend to be smaller, and to be associated with Q
![]() $^{-}$
s. In channels, they are preferentially associated with Q2s, but the statistical symmetries of HST require that they should be equally distributed between Q2s and Q4s. The preferential association in channels must therefore be due to the inhomogeneity of the mean profile. Presumably, since ejections come from points closer to the wall where the shear is stronger, they carry with them the higher enstrophy of those layers. Table 4 shows that the fraction of Reynolds stresses carried by the different quadrants in HST is approximately the same as in the logarithmic layer of channels, including the fraction of Q
$^{-}$
s. In channels, they are preferentially associated with Q2s, but the statistical symmetries of HST require that they should be equally distributed between Q2s and Q4s. The preferential association in channels must therefore be due to the inhomogeneity of the mean profile. Presumably, since ejections come from points closer to the wall where the shear is stronger, they carry with them the higher enstrophy of those layers. Table 4 shows that the fraction of Reynolds stresses carried by the different quadrants in HST is approximately the same as in the logarithmic layer of channels, including the fraction of Q
![]() $^{+}$
‘momentum backscatter’.
$^{+}$
‘momentum backscatter’.
Both channels and HST burst intermittently (see § 3). The effect is made more obvious in the latter by the unavoidably ‘minimal’ character of statistically stationary HST, but we have shown that the structure of turbulence during HST bursts can largely be modelled by a variable threshold in the definition of the structures.
The geometry of the Q
![]() $^{-}$
s is self-similar for diameters
$^{-}$
s is self-similar for diameters
![]() $d\gtrsim 50\unicode[STIX]{x1D702}$
, with essentially isotropic aspect ratios similar to those of detached Qs in channels (see § 4.3). This remains approximately true for larger detached structures
$d\gtrsim 50\unicode[STIX]{x1D702}$
, with essentially isotropic aspect ratios similar to those of detached Qs in channels (see § 4.3). This remains approximately true for larger detached structures
![]() $(d\gtrsim L_{c})$
in channels and in HST, and we have shown in § 4.4 that the more elongated aspect ratios of attached channel Qs are a property of strictly attached structures
$(d\gtrsim L_{c})$
in channels and in HST, and we have shown in § 4.4 that the more elongated aspect ratios of attached channel Qs are a property of strictly attached structures
![]() $(y_{min}^{+}<20)$
, most probably due to ‘spurious’ connections between the viscous near-wall roots of otherwise unrelated eddies. Conversely, we have shown that the relative arrangement of Q
$(y_{min}^{+}<20)$
, most probably due to ‘spurious’ connections between the viscous near-wall roots of otherwise unrelated eddies. Conversely, we have shown that the relative arrangement of Q
![]() $^{-}$
s of the same type suggests that many of them are ‘spurious’ fragments of larger structures, separated from one another by the thresholding operation.
$^{-}$
s of the same type suggests that many of them are ‘spurious’ fragments of larger structures, separated from one another by the thresholding operation.
Section 5 shows that many of the differences between the flow within and outside Qs can be traced to the way in which they are defined. For example, the increased anisotropy of the Reynolds-stress tensor within Qs can be reproduced by thresholding a joint-Gaussian distribution of
![]() $u$
and
$u$
and
![]() $v$
with the right correlation coefficient (figure 4). We have also noted that structures that are too small to couple with the shear
$v$
with the right correlation coefficient (figure 4). We have also noted that structures that are too small to couple with the shear
![]() $(d\ll L_{c})$
have no preferred orientation, and cannot be usefully classified into quadrants. Small Qs of the same kind (e.g. Q4 with Q4) are preferentially aligned along the direction of their velocity fluctuations, while Qs of opposite kind (e.g. Q2 with Q4) tend to exclude each other from the direction of their axis, and arrange equatorially with respect to each other. This generalises the arrangement of attached pairs in channels, where Q2s and Q4s are organised into streamwise trains of side-by-side pairs.
$(d\ll L_{c})$
have no preferred orientation, and cannot be usefully classified into quadrants. Small Qs of the same kind (e.g. Q4 with Q4) are preferentially aligned along the direction of their velocity fluctuations, while Qs of opposite kind (e.g. Q2 with Q4) tend to exclude each other from the direction of their axis, and arrange equatorially with respect to each other. This generalises the arrangement of attached pairs in channels, where Q2s and Q4s are organised into streamwise trains of side-by-side pairs.
Larger Qs lose this isotropy and organise themselves in true spanwise pairs, but only in the case of
![]() $(uv)$
structures. It is possible to define quadrant structures from other combinations of velocity components, such as Q
$(uv)$
structures. It is possible to define quadrant structures from other combinations of velocity components, such as Q
![]() $_{uw}$
. They differ little from Q
$_{uw}$
. They differ little from Q
![]() $_{uv}$
for small sizes, but they never interact with the shear and do not change character for sizes above
$_{uv}$
for small sizes, but they never interact with the shear and do not change character for sizes above
![]() $L_{c}$
. The difference is most obvious for counter-gradient Q
$L_{c}$
. The difference is most obvious for counter-gradient Q
![]() $^{+}$
s (Q1 and Q3), which couple with the shear for large sizes, but lose energy in the interaction instead of gaining it. As a consequence, there are essentially no large Q
$^{+}$
s (Q1 and Q3), which couple with the shear for large sizes, but lose energy in the interaction instead of gaining it. As a consequence, there are essentially no large Q
![]() $^{+}$
s in channels or in HST.
$^{+}$
s in channels or in HST.
We have shown in § 5.2 that the deviations from isotropy of the relative position of Qs of different kind imply that they are preferentially located in strong shear layers separating regions of relatively uniform velocity within the high- and low-velocity streaks, in agreement with previous observations of uniform momentum regions (regions) in wall-bounded flows. The conditional flow fields around close pairs of Qs of opposite sign, discussed in § 6, clearly show this layer, as well as a fairly strong roller that organises the pair, inclined along the most extensive direction of the shear of the mean velocity (Rogers & Moin Reference Rogers and Moin1987). We have shown that the conditional shear layer is different from the coherent conditional ‘roller’, as well as from the conditional vortex cluster also associated with the Q pair.
As mentioned above, the primary goal of this study was to distinguish between those properties of the structures of wall turbulence that are due to the presence of the wall from those simply due to the shear. A particularly interesting set of conditional flow fields is displayed in figure 14, which shows how the flow around a Q2–Q4 pair progressively changes from the homogeneous HST to the very inhomogeneous velocity profile near the wall in channels. The diagonal rollers of HST morph into quasi-streamwise ones near the wall. It is interesting that all of these rollers contain hairpin ‘hooks’, although we emphasise that the rollers are large-scale conditional structures, not features of the resolved vorticity. The HST hairpins include both upright and inverted hooks, as observed in simulations and experiments of homogeneous shear (Rogers & Moin Reference Rogers and Moin1987; Vanderwel & Tavoularis Reference Vanderwel and Tavoularis2011). The inverted hook weakens as it is progressively absorbed into the inhomogeneous stronger vorticity near the wall, but there is no indication that the upright one has a different origin in wall-less HST from that in the near-wall channel.
The conclusion is that most properties of the strong tangential-stress structures, and of the vorticity clusters, should apply to general shear flows, or at least to those in which no other turbulence production mechanism is dominant. Obvious exceptions that come to mind are free-shear flows subject to Kelvin–Helmholtz-type instabilities of the mean velocity profile (Brown & Roshko Reference Brown and Roshko1974). Moreover, the observed decoupling between small Qs and the ambient shear suggests that similar structures should be generic to turbulence in general, whether sheared or not.
Acknowledgements
This work was supported by the European Research Council under grants ERC-2010.AdG-20100224 and ERC-2014.AdG-669505. S.D. was supported by the China Scholarship Council. We acknowledge PRACE for access to the BG/Q computer at the Jülich Supercomputing Centre, and RES for access to the Barcelona Supercomputing Centre.