Hostname: page-component-77c89778f8-9q27g Total loading time: 0 Render date: 2024-07-19T08:18:22.791Z Has data issue: false hasContentIssue false
  • English
  • Français

Boussinesq global modes and stability sensitivity, with applications to stratified wakes

Published online by Cambridge University Press:  12 January 2017

Kevin K. Chen Open the ORCID record for Kevin K. Chen [Opens in a new window]  and
Geoffrey R. Spedding
Kevin K. Chen
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA
Geoffrey R. Spedding
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

For the Boussinesq equations, we present a theory of linear stability sensitivity to base flow density and velocity modifications. Given a steady-state flow with small density variations, the sensitivity of the stability eigenvalues is computed from the direct and adjoint global modes of the linearised Boussinesq equations, similarly to Marquet et al. (J. Fluid Mech., vol. 615, 2008, pp. 221–252). Combinations of the density and velocity components of these modes reveal multiple production and transport mechanisms that contribute to the eigenvalue sensitivity. We present an application of the sensitivity theory to a stably linearly density-stratified flow around a thin plate at a 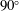$90^{\circ }$ angle of attack, a Reynolds number of 30 and Froude numbers of 1, 8 and 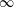$\infty$. The global mode analysis reveals lightly damped undulations pervading through the entire domain, which are predicted by both inviscid uniform base flow theory and Orr–Sommerfeld theory. The sensitivity to base flow velocity modifications is primarily concentrated just downstream of the bluff body. On the other hand, the sensitivity to base flow density modifications is concentrated in regions both immediately upstream and immediately downstream of the plate. Both sensitivities have a greater upstream presence for lower Froude numbers.

JFM classification

Instability: Instability Geophysical and Geological Flows: Stratified flows Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 1146 - 1188
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

van Atta, C. W. & Hopfinger, E. J. 1989 Vortex ring instability and collapse in a stably stratified fluid. Exp. Fluids 7, 197–200.Google Scholar
Bagheri, S., Henningson, D. S., Hœpffner, J. & Schmid, P. J. 2009 Input–output analysis and control design applied to a linear model of spatially developing flows. Appl. Mech. Rev. 62, 020803.CrossRefGoogle Scholar
Barbagallo, A., Sipp, D. & Schmid, P. J. 2009 Closed-loop control of an open cavity flow using reduced-order models. J. Fluid Mech. 641, 1–50.Google Scholar
Billant, P. & Chomaz, J.-M. 2000 Experimental evidence for a new instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 418, 167–188.Google Scholar
Bosco, M. & Meunier, P. 2014 Three-dimensional instabilities of a stratified cylinder wake. J. Fluid Mech. 759, 149–180.Google Scholar
Bottaro, A., Corbett, P. & Luchini, P. 2003 The effect of base flow variation on flow stability. J. Fluid Mech. 476, 293–302.Google Scholar
Boujo, E. & Gallaire, F. 2014 Manipulating flow separation: sensitivity of stagnation points, separatrix angles and recirculation area to steady actuation. Proc. R. Soc. Lond. A 470, 20140365.Google Scholar
Boulanger, N., Meunier, P. & Le Dizès, S. 2008 Tilt-induced instability of a stratified vortex. J. Fluid Mech. 596, 1–20.CrossRefGoogle Scholar
Candelier, J., Le Dizès, S. & Millet, C. 2011 Shear instability in a stratified fluid when shear and stratification are not aligned. J. Fluid Mech. 685, 191–201.Google Scholar
Chandler, G. J., Juniper, M. P., Nichols, J. W. & Schmid, P. J. 2012 Adjoint algorithms for the Navier–Stokes equations in the low Mach number limit. J. Comput. Phys. 231, 1900–1916.Google Scholar
Chen, K. K., Rowley, C. W. & Stone, H. A. 2015 Vortex dynamics in a pipe T-junction: recirculation and sensitivity. Phys. Fluids 27, 034107.Google Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability, 2nd edn. Cambridge Mathematical Library. Cambridge University Press.Google Scholar
Fani, A., Camarri, S. & Salvetti, M. V. 2013 Investigation of the steady engulfment regime in a three-dimensional T-mixer. Phys. Fluids 25, 064102.Google Scholar
Ferziger, J. H. & Perić, M. 2002 Computational Methods for Fluid Dynamics, 3rd edn. Springer.CrossRefGoogle Scholar
Garrett, C. & Munk, W. 1979 Internal waves in the ocean. Annu. Rev. Fluid Mech. 11 (1), 339–369.Google Scholar
Giannetti, F., Camarri, S. & Luchini, P. 2010 Structural sensitivity of the secondary instability in the wake of a circular cylinder. J. Fluid Mech. 651, 319–337.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.Google Scholar
Gourlay, M. J., Arendt, S. C., Fritts, D. C. & Werne, J. 2001 Numerical modeling of initially turbulent wakes with net momentum. Phys. Fluids 13, 3783–3802.Google Scholar
Gresho, P. M. & Sani, R. L. 1987 On pressure boundary conditions for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 7, 1111–1145.Google Scholar
Hill, D. C.1992 A theoretical approach for analyzing the restabilization of wakes. In 30th AIAA Aerospace Sciences Meeting & Exhibit, AIAA Paper 92-0067, American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Issa, R. I. 1986 Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65.Google Scholar
Issa, R. I., Gosman, A. D. & Watkins, A. P. 1986 The computation of compressible and incompressible recirculating flows by a non-iterative implicit scheme. J. Comput. Phys. 62, 66–82.Google Scholar
Johari, H. & Fang, H. 1997 Horizontal vortex ring motion in linearly stratified media. Phys. Fluids 9, 2605–2616.Google Scholar
Kaminski, A. K., Caulfield, C. P. & Taylor, J. R. 2014 Transient growth in strongly stratified shear layers. J. Fluid Mech. 758, R4.Google Scholar
Koppel, D. 1964 On the stability of flow of a thermally stratified fluid under the action of gravity. J. Math. Phys. 5, 963–982.CrossRefGoogle Scholar
Lashgari, I., Tammisola, O., Citro, V., Juniper, M. P. & Brandt, L. 2014 The planar X-junction flow: stability analysis and control. J. Fluid Mech. 753, 1–28.Google Scholar
Le Dizès, S. & Billant, P. 2009 Radiative instability in stratified vortices. Phys. Fluids 21, 096602.Google Scholar
Lin, J. T. & Pao, Y. H. 1979 Wakes in stratified fluids. Annu. Rev. Fluid Mech. 11, 317–338.Google Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
Maslowe, S. A. & Thompson, J. M. 1971 Stability of a stratified free shear layer. Phys. Fluids 14, 453–458.Google Scholar
Meliga, P., Boujo, E., Pujals, G. & Gallaire, F. 2014 Sensitivity of aerodynamic forces in laminar and turbulent flow past a square cylinder. Phys. Fluids 26, 104101.CrossRefGoogle Scholar
Meliga, P., Pujals, G. & Serre, E. 2012 Sensitivity of 2-D turbulent flow past a D-shaped cylinder using global stability. Phys. Fluids 24, 061701.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.Google Scholar
Negretti, M. E. & Billant, P. 2013 Stability of a Gaussian pancake vortex in a stratified fluid. J. Fluid Mech. 718, 457–480.CrossRefGoogle Scholar
Ortiz, S., Donnadieu, C. & Chomaz, J.-M. 2015 Three-dimensional instabilites and optimal perturbations of a counter-rotating vortex pair in stratified flows. Phys. Fluids 27, 106603.Google Scholar
Qadri, U. A., Mistry, D. & Juniper, M. P. 2013 Structural sensitivity of spiral vortex breakdown. J. Fluid Mech. 720, 558–581.CrossRefGoogle Scholar
Rhines, P. B. 1979 Geostrophic turbulence. Annu. Rev. Fluid Mech. 11, 401–441.Google Scholar
Riley, J. J. & Lelong, M.-P. 2000 Fluid motions in the presence of strong stable stratification. Annu. Rev. Fluid Mech. 32, 613–657.Google Scholar
Schmid, P. J. & Brandt, L. 2014 Analysis of fluid systems: stability, receptivity, sensitivity. Appl. Mech. Rev. 66, 024803.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows, Applied Mathematical Sciences, vol. 142. Springer.Google Scholar
Spedding, G. R. 2014 Wake signature detection. Annu. Rev. Fluid Mech. 46, 273–302.CrossRefGoogle Scholar
de Stadler, M. B., Sarkar, S. & Brucker, K. A. 2010 Effect of the Prantdl number on a stratified turbulent wake. Phys. Fluids 22, 095102.Google Scholar
Strykowski, P. J. & Sreenivasan, K. R. 1990 On the formation and suppression of vortex ‘shedding’ at low Reynolds numbers. J. Fluid Mech. 218, 71–107.Google Scholar
Trefethen, L. N. & Bau, D. III 1997 Numerical Linear Algebra. Society for Industrial and Applied Mathematics.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261, 578–584.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.CrossRefGoogle Scholar
Voisin, B. 1991 Internal wave generation in uniformly stratified fluids. Part 1. Green’s function and point sources. J. Fluid Mech. 231, 439–480.CrossRefGoogle Scholar
Weideman, J. A. C. & Reddy, S. C. 2000 A MATLAB differentiation matrix suite. ACM Trans. Math. Softw. 26, 465–519.Google Scholar
Weller, H. H., Tabor, G., Jasak, H. & Fureby, C. 1998 A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 12, 620–631.Google Scholar
White, F. M. 2005 Viscous Fluid Flow, 3rd edn. McGraw-Hill.Google Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314.Google Scholar
Yih, C. S. 1969 Stratified flows. Annu. Rev. Fluid Mech. 1, 73–110.Google Scholar