Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-25T08:18:30.162Z Has data issue: false hasContentIssue false
  • English
  • Français

The Basset problem with dynamic slip: slip-induced memory effect and slip–stick transition

Published online by Cambridge University Press:  13 March 2019

A. R. Premlata  and
Hsien-Hung Wei Open the ORCID record for Hsien-Hung Wei [Opens in a new window]
A. R. Premlata
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
Hsien-Hung Wei*
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
*
†Email address for correspondence: hhwei@mail.ncku.edu.tw
Get access Rights & Permissions [Opens in a new window]

Abstract

When there exists slip on the surface of a solid body moving in an unsteady manner, the extent of slip is not fixed but constantly changes with the time-varying Stokes boundary layer thickness 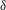$\unicode[STIX]{x1D6FF}$ in competition with the slip length 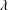$\unicode[STIX]{x1D706}$. Here we revisit the unsteady motion of a slippery spherical particle to elucidate this dynamic slip situation. We find that even if the amount of slip is minuscule, it can dramatically change the characteristics of the history force, markedly different from those due to non-spherical and fluid particles (Lawrence & Weinbaum, J. Fluid Mech., vol. 171, 1986, pp. 209–218; Yang & Leal, Phys. Fluids A, vol. 3, 1991, pp. 1822–1824). For an oscillatory translation of such a particle of radius $a$, two distinctive features are identified in the frequency response of the viscous drag: (i) the high-frequency constant force plateau of 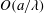$O(a/\unicode[STIX]{x1D706})$ much greater than the steady drag due to a constant shear stress caused by 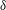$\unicode[STIX]{x1D6FF}$ much thinner than 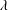$\unicode[STIX]{x1D706}$ and (ii) the persistence of the plateau while lowering the frequency until the slip–stick transition point 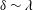$\unicode[STIX]{x1D6FF}\sim \unicode[STIX]{x1D706}$, beyond which $\unicode[STIX]{x1D6FF}$ becomes thicker and the usual Basset decay reappears. Similar features can also be observed in the short-term force response for the particle subject to a sudden movement, as well as in the behaviour of the torque when it undergoes rotary oscillations. In addition, for both translational and rotary oscillations, slip can further introduce a phase jump from the no-slip value to zero in the high-frequency limit. As these features and the associated slip–stick transitions become more evident as 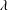$\unicode[STIX]{x1D706}$ becomes smaller and are exclusive to the situation where surface slip is present, they might have potential uses for extracting the slip length of a colloidal particle from experiments.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 866 , 10 May 2019 , pp. 431 - 449
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albano, A. M., Bedeaux, D. & Mazur, P. 1975 On the motion of a sphere with arbitrary slip in a viscous incompressible fluid. Physica A 80, 89–97.10.1016/0378-4371(75)90148-XGoogle Scholar
Ashmawy, E. A. 2012 Unsteady rotational motion of a slip spherical particle in a viscous fluid. ISRN Math. Phys. 2012, 513717.10.5402/2012/513717Google Scholar
Ashmawy, E. A. 2017 Unsteady translational motion of a slip sphere in a viscous fluid using the fractional Navier–Stokes equation. Eur. Phys. J. Plus 132 (3), 142.Google Scholar
Basset, A. B. 1888 On the motion of a sphere in a viscous liquid. Phil. Trans. R. Soc. Lond. A 179, 43–63.10.1098/rsta.1888.0003Google Scholar
Bentwich, M. & Miloh, T. 1978 The unsteady matched Stokes–Oseen solution for the flow past a sphere. J. Fluid Mech. 88, 17–32.10.1017/S0022112078001962Google Scholar
Felderhof, B. U. 1976 Force density induced on a sphere in linear hydrodynamics: II. Moving sphere, mixed boundary conditions. Physica A 84, 569–576.10.1016/0378-4371(76)90105-9Google Scholar
Feng, J. & Joseph, D. D. 1995 The unsteady motion of solid bodies in creeping flows. J. Fluid Mech. 303, 83–102.10.1017/S0022112095004186Google Scholar
Fujioka, H. & Wei, H.-H. 2018 Letter: new boundary layer structures due to strong wall slippage. Phys. Fluids 30 (12), 121702.Google Scholar
Galindo, V. & Gerbeth, G. 1993 A note on the force on an accelerating spherical drop at low-Reynolds number. Phys. Fluids A 5, 3290–3292.10.1063/1.858686Google Scholar
Garbin, V., Dollet, B., Overvelde, M., Cojoc, D., Di Fabrizio, E., Van Wijngaarden, L., Prosperetti, A., De Jong, N., Lohse, D. & Versluis, M. 2009 History force on coated microbubbles propelled by ultrasound. Phys. Fluids 21 (9), 092003.10.1063/1.3227903Google Scholar
Gatignol, R. 2007 On the history term of Boussinesq–Basset when the viscous fluid slips on the particle. C. R. Méc. 335, 606–616.10.1016/j.crme.2007.08.013Google Scholar
Kim, S. & Karrila, S. J. 1991 Microhydrodynamics: Principles and Selected Applications. Butterworth–Heinemann.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics. Pergamon.Google Scholar
Laurell, T., Petersson, F. & Nilsson, A. 2007 Chip integrated strategies for acoustic separation and manipulation of cells and particles. Chem. Soc. Rev. 36 (3), 492–506.10.1039/B601326KGoogle Scholar
Lawrence, C. J. & Weinbaum, S. 1986 The force on an axisymmetric body in linearized, time-dependent motion: a new memory term. J. Fluid Mech. 171, 209–218.10.1017/S0022112086001428Google Scholar
Lawrence, C. J. & Weinbaum, S. 1988 The unsteady force on a body at low Reynolds number: the axisymmetric motion of a spheroid. J. Fluid Mech. 189, 463–489.10.1017/S0022112088001107Google Scholar
Lovalenti, P. M. & Brady, J. F. 1993 The force on a bubble, drop, or particle in arbitrary time-dependent motion at small Reynolds number. Phys. Fluids A 5 (9), 2104–2116.10.1063/1.858550Google Scholar
Magnaudet, J. & Legendre, D. 1998 The viscous drag force on a spherical bubble with a time-dependent radius. Phys. Fluids 10 (3), 550–554.10.1063/1.869582Google Scholar
Michaelides, E. E. & Feng, Z. G. 1995 The equation of motion of a small viscous sphere in an unsteady flow with interface slip. Intl J. Multiphase Flow 21, 315–321.10.1016/0301-9322(94)00066-SGoogle Scholar
Pozrikidis, C. 1989 A singularity method for unsteady linearized flow. Phys. Fluids A 1, 1508–1520.10.1063/1.857329Google Scholar
Simha, A., Mo, J. & Morrison, P. J. 2018 Unsteady Stokes flow near boundaries: the point-particle approximation and the method of reflections. J. Fluid Mech. 841, 883–924.10.1017/jfm.2018.87Google Scholar
Takemura, F. & Magnaudet, J. 2004 The history force on a rapidly shrinking bubble rising at finite Reynolds number. Phys. Fluids 16 (9), 3247–3255.10.1063/1.1760691Google Scholar
Wang, S. & Ardekani, A. M. 2012 Unsteady swimming of small organisms. J. Fluid Mech. 702, 286–297.10.1017/jfm.2012.177Google Scholar
Yang, S. M. & Leal, L. G. 1991 A note on memory-integral contributions to the force on an accelerating spherical drop at low Reynolds number. Phys. Fluids A 3, 1822–1824.10.1063/1.858202Google Scholar
Yih, C.-S. 1977 Fluid Mechanics: A Concise Introduction to the Theory. West River Press.Google Scholar
Zhang, W. & Stone, H. A. 1998 Oscillatory motions of circular disks and nearly spherical particles in viscous flows. J. Fluid Mech. 367, 329–358.10.1017/S0022112098001670Google Scholar