Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ayton, Lorna J.
and
Kim, Jae Wook
2018.
An analytic solution for the noise generated by gust–aerofoil interaction for plates with serrated leading edges.
Journal of Fluid Mechanics,
Vol. 853,
Issue. ,
p.
515.
Miotto, Renato F.
Wolf, William
de Santana, Leandro D.
and
Venner, Cornelis H.
2018.
Application of Amiet's theory for noise prediction of general airfoil profiles subjected to spanwise-varying inflow conditions.
Miotto, Renato F.
Wolf, William R.
and
de Santana, Leandro D.
2018.
Leading-Edge Noise Prediction of General Airfoil Profiles with Spanwise-Varying Inflow Conditions.
AIAA Journal,
Vol. 56,
Issue. 5,
p.
1711.
Massarotti, Maurício R.
and
Wolf, William R.
2018.
Aeroacoustic analysis of automotive roof crossbars through on-track acoustic measurements.
Applied Acoustics,
Vol. 142,
Issue. ,
p.
95.
Ayton, Lorna J.
and
Chaitanya, Paruchuri
2019.
An analytical and experimental investigation of aerofoil–turbulence interaction noise for plates with spanwise-varying leading edges.
Journal of Fluid Mechanics,
Vol. 865,
Issue. ,
p.
137.
Zhong, Siyang
Jiang, Hanbo
Ying, Wei
and
Zhang, Xin
2019.
An analytical model for the prediction of airfoil cascade-turbulence interaction noise.
Zhong, Siyang
and
Zhang, Xin
2019.
On the effect of streamwise disturbance on the airfoil-turbulence interaction noise.
The Journal of the Acoustical Society of America,
Vol. 145,
Issue. 4,
p.
2530.
Zhong, Siyang
Jiang, Hanbo
Ying, Wei
Zhang, Xin
and
Huang, Xun
2019.
An efficient computation of cascade-gust interaction noise based on a hybrid analytical and boundary element method.
Journal of Sound and Vibration,
Vol. 461,
Issue. ,
p.
114911.
Zhong, Siyang
and
Zhang, Xin
2019.
Numerical and analytical investigations of the effect of the streamwise disturbance on the airfoil-anisotropic turbulence interaction noise.
Zhong, Siyang
Zhang, Xin
Peng, Bo
and
Huang, Xun
2020.
An analytical correction to Amiet’s solution of airfoil leading-edge noise in non-uniform mean flows.
Journal of Fluid Mechanics,
Vol. 882,
Issue. ,
Jaworski, Justin W.
and
Peake, N.
2020.
Aeroacoustics of Silent Owl Flight.
Annual Review of Fluid Mechanics,
Vol. 52,
Issue. 1,
p.
395.
Karimi, M.
Croaker, P.
Skvortsov, A.
Maxit, L.
and
Kirby, R.
2021.
Simulation of airfoil surface pressure due to incident turbulence using realizations of uncorrelated wall plane waves.
The Journal of the Acoustical Society of America,
Vol. 149,
Issue. 2,
p.
1085.
dos Santos, Fernanda Leticia
Botero, Laura
Venner, Cornelis
and
de Santana, Leandro D.
2022.
On the turbulence distortion effects for airfoil leading-edge noise prediction.
dos Santos, Fernanda L.
Botero-Bolívar, Laura
Venner, Cornelis H.
and
de Santana, Leandro D.
2023.
Inflow turbulence distortion for airfoil leading-edge noise prediction for large turbulence length scales for zero-mean loading.
The Journal of the Acoustical Society of America,
Vol. 153,
Issue. 3,
p.
1811.
Ribeiro, André F. P.
dos Santos, Fernanda L.
Venner, Kees
and
de Santana, Leandro D.
2023.
Numerical study of inflow turbulence distortion and noise for airfoils.
Physics of Fluids,
Vol. 35,
Issue. 11,
dos Santos, Fernanda Leticia
Venner, Cornelis H.
and
de Santana, Leandro D.
2023.
Study of the Inflow Turbulence Distortion for Airfoils and Cylinders.
Jiang, Shujie
Wang, Yanan
Yan, Zhenguo
Zhang, Rongping
and
Hu, Zhiwei
2023.
Variations with Mach number for gust–airfoil interaction noise.
Physics of Fluids,
Vol. 35,
Issue. 2,
Kha, Jamie
Croaker, Paul
Karimi, Mahmoud
and
Skvortsov, Alex
2024.
Uncertainty Analysis in Airfoil–Turbulence Interaction Noise Using Polynomial Chaos Expansion.
AIAA Journal,
Vol. 62,
Issue. 2,
p.
657.
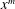 $x^{m}$ for
$x^{m}$ for 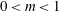 $0<m<1$. Rapid distortion theory governs the interaction of an unsteady vortical perturbation with a rigid aerofoil in compressible steady mean flow that is uniform far upstream. For high-frequency gusts interacting with aerofoils of small total thickness this allows a matched asymptotic solution to be obtained. This paper mainly focusses on obtaining the analytic solution in the leading-edge inner region, which is the dominant term in determining the total far-field acoustic directivity, and contains the effects of the local leading-edge geometry. Experimental measurements for the noise generated by aerofoils with different leading-edge nose radii in uniform flow with approximate homogeneous, isotropic turbulence are also presented. Both experimental and analytic results predict that a larger nose radius generates less overall noise in low-Mach-number flow. By considering individual terms in the analytic solution, this paper is able to propose reasons behind this result.
$0<m<1$. Rapid distortion theory governs the interaction of an unsteady vortical perturbation with a rigid aerofoil in compressible steady mean flow that is uniform far upstream. For high-frequency gusts interacting with aerofoils of small total thickness this allows a matched asymptotic solution to be obtained. This paper mainly focusses on obtaining the analytic solution in the leading-edge inner region, which is the dominant term in determining the total far-field acoustic directivity, and contains the effects of the local leading-edge geometry. Experimental measurements for the noise generated by aerofoils with different leading-edge nose radii in uniform flow with approximate homogeneous, isotropic turbulence are also presented. Both experimental and analytic results predict that a larger nose radius generates less overall noise in low-Mach-number flow. By considering individual terms in the analytic solution, this paper is able to propose reasons behind this result.




