Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-19T23:00:17.467Z Has data issue: false hasContentIssue false
  • English
  • Français

An extended linear shallow-water equation

Published online by Cambridge University Press:  01 August 2019

R. Porter Open the ORCID record for R. Porter [Opens in a new window]
R. Porter*
Affiliation:
School of Mathematics, University of Bristol, Bristol BS8 1TW, UK
*
†Email address for correspondence: richard.porter@bris.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

An extension to the classical shallow-water equation (SWE) is derived that exactly satisfies the bed condition and can be regarded as an approximation to wave scattering at the next order in the small parameter 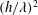$(h/\unicode[STIX]{x1D706})^{2}$ (depth to wavelength ratio squared). In the frequency domain, the extended SWE shares the same simple structure as the standard SWE with coefficients modified by terms relating to the bed variation. In three dimensions the governing equation demonstrates that variable topography gives rise to anisotropic effects on wave scattering not present in the standard SWE, with consequences for the design of water wave metamaterials. Numerical examples illustrate that approximations to wave scattering using the extended SWE are significantly improved in comparison with the standard SWE.

JFM classification

Waves/Free-surface Flows: Wave scattering Waves/Free-surface Flows: Surface gravity waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 876 , 10 October 2019 , pp. 413 - 427
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berraquero, C. P., Maurel, A., Petitjeans, P. & Pagneux, V. 2013 Experimental realization of a water-wave metamaterial shifter. Phys. Rev. E 88, 051002.Google Scholar
Booij, N. 1983 A note on the accuracy of the mild-slope equation. Coast. Engng 7, 191–203.Google Scholar
Brocchini, M. 2013 A reasoned overview on Boussinesq-type models: the interplay between physics, mathematics and numerics. Proc. R. Soc. Lond. A 469, 20130496.Google Scholar
Chen, H., Yang, J., Zi, J. & Chan, C. T. 2009 Transformation media for linear liquid surface waves. Europhys. Lett. 85, 24004.Google Scholar
Cho, Y.-S., Sohn, D.-H. & Lee, S. O. 2007 Practical modified scheme of linear shallow-water equations for distant propagation of tsunamis. Ocean Engng 34, 1769–1777.Google Scholar
Dias, F. & Milewski, P. 2010 On the fully-nonlinear shallow-water generalized Serre equations. Phys. Lett. A 374, 1049–1053.Google Scholar
Dupont, G., Kimmoun, O., Molin, B., Guenneau, S. & Enoch, S. 2015 Numerical and experimental study of an invisibility carpet in a water channel. Phys. Rev. E 91, 023010.Google Scholar
Duran, A., Dutykh, D. & Mitsotakis, M. 2018 Peregrine’s system revisited. In Nonlinear Waves and Pattern Dynamics, Springer.Google Scholar
Ehrenmark, U. T. 2005 An alternative dispersion relation for water waves over an inclined bed. J. Fluid Mech. 543, 249–266.Google Scholar
Farhat, M., Enoch, S., Guenneau, S. & Movchan, A. 2008 Broadband cylindrical acoustic cloak for linear surface waves in a fluid. Phys. Rev. Lett. 101, 134501.Google Scholar
Farhat, M., Guenneau, S., Enoch, S. & Movchan, A. 2010 All-angle-negative-refraction and ultra-refraction for liquid surface waves in 2D phononic crystals. J. Comput. Appl. Maths 234 (6), 2011–2019.Google Scholar
Friedrichs, K. O. 1948 Water waves on a shallow sloping beach. Commun. Pure Appl. Maths 1, 109–134.Google Scholar
Green, A. & Naghdi, P. 1976 A derivation of equations for wave propagation in water of variable depth. J. Fluid Mech. 78, 237–246.Google Scholar
Hu, X., Chan, C. T., Ho, K.-M. & Zi, J. 2011 Negative effective gravity in water waves by periodic resonator arrays. Phys. Rev. Lett. 106, 174501.Google Scholar
Kim, J. W. & Bai, K. J. 2004 A new complementary mild-slope equation. J. Fluid Mech. 511, 25–40.Google Scholar
Lamb, H. 1932 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Madsen, P. A., Murray, R. & Sbrensen, O. R. 1991 A new form of Boussinesq equations with improved linear dispersion characteristics. Coast. Engng 15, 371–388.Google Scholar
Maurel, A., Marigo, J.-J., Cobelli, P., Petitjeans, P. & Pagneux, V. 2017 Revisiting the anisotropy of metamaterials for water waves. Phys. Rev. B 96, 134310.Google Scholar
Mei, C. C. & Le Méhauté, B. 1966 Note on the equations of long waves over an uneven bottom. J. Geophys. Res. 71 (2), 393–400.Google Scholar
Peregrine, D. H. 1967 Long waves on a beach. J. Fluid Mech. 27, 815–827.Google Scholar
Porter, D. 2003 The mild slope equations. J. Fluid Mech. 494, 51–63.Google Scholar
Porter, D. & Porter, R. 2006 Approximations to water wave scattering by steep topography. J. Fluid Mech. 562, 279–302.Google Scholar
Porter, R. & Porter, D. 2000 Water wave scattering by a step of arbitrary profile. J. Fluid Mech. 411, 131–164.Google Scholar
Roseau, M. 1976 Asymptotic Wave Theory, North-Holland Series in Applied Mathematics and Mechanics, vol. 2. North-Holland Publ. Company.Google Scholar
Stoker, J. J. 1957 Water Waves. Interscience.Google Scholar
Toledo, Y. & Agnon, Y. 2010 A scalar form of the complementary mild-slope equation. J. Fluid Mech. 656, 407–416.Google Scholar
Ursell, F. 1953 The long-wave paradox in the theory of gravity waves. Proc. Camb. Phil. Soc. 49 (4), 685–694.Google Scholar
Wang, Z., Zhang, P., Nie, X. & Zhang, Y. 2015 Manipulating water wave propagation via gradient index media. Sci. Rep. 5, 16846.Google Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley-Interscience.Google Scholar