Article contents
The turbulent Kármán vortex
Published online by Cambridge University Press: 17 May 2019
Abstract
This work focuses on the temperature (passive scalar) and velocity characteristics within a turbulent Kármán vortex using a phase-averaging technique. The vortices are generated by a circular cylinder, and the three components of the fluctuating velocity and vorticity vectors, 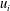 $u_{i}$ and
$u_{i}$ and 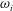 $\unicode[STIX]{x1D714}_{i}$ (
$\unicode[STIX]{x1D714}_{i}$ (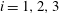 $i=1,2,3$), are simultaneously measured, along with the fluctuating temperature
$i=1,2,3$), are simultaneously measured, along with the fluctuating temperature 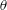 $\unicode[STIX]{x1D703}$ and the temperature gradient vector, at nominally the same spatial point in the plane of mean shear at
$\unicode[STIX]{x1D703}$ and the temperature gradient vector, at nominally the same spatial point in the plane of mean shear at 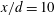 $x/d=10$, where
$x/d=10$, where  $x$ is the streamwise distance from the cylinder axis and
$x$ is the streamwise distance from the cylinder axis and 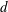 $d$ is the cylinder diameter. We believe this is the first time the properties of fluctuating velocity, temperature, vorticity and temperature gradient vectors have been explored simultaneously within the Kármán vortex in detail. The Reynolds number based on
$d$ is the cylinder diameter. We believe this is the first time the properties of fluctuating velocity, temperature, vorticity and temperature gradient vectors have been explored simultaneously within the Kármán vortex in detail. The Reynolds number based on 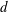 $d$ and the free-stream velocity is
$d$ and the free-stream velocity is 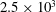 $2.5\times 10^{3}$. The phase-averaged distributions of
$2.5\times 10^{3}$. The phase-averaged distributions of 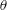 $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and 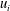 $u_{i}$ follow closely the Gaussian distribution for
$u_{i}$ follow closely the Gaussian distribution for 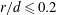 $r/d\leqslant 0.2$ (
$r/d\leqslant 0.2$ ( $r$ is the distance from the vortex centre), but not for
$r$ is the distance from the vortex centre), but not for 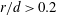 $r/d>0.2$. The collapse of the distributions of the mean-square streamwise derivative of the velocity fluctuations within the Kármán vortex implies that the velocity field within the vortex tends to be more locally isotropic than the flow field outside the vortex. A possible physical explanation is that the large and small scales of velocity and temperature fields are statistically independent of each other near the Kármán vortex centre, but interact vigorously outside the vortex, especially in the saddle region, due to the action of coherent strain rate.
$r/d>0.2$. The collapse of the distributions of the mean-square streamwise derivative of the velocity fluctuations within the Kármán vortex implies that the velocity field within the vortex tends to be more locally isotropic than the flow field outside the vortex. A possible physical explanation is that the large and small scales of velocity and temperature fields are statistically independent of each other near the Kármán vortex centre, but interact vigorously outside the vortex, especially in the saddle region, due to the action of coherent strain rate.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 6
- Cited by


