Article contents
A stable tripole vortex model in two-dimensional Euler flows
Published online by Cambridge University Press: 17 September 2019
Abstract
An exact solution of a stable vortex tripole in two-dimensional (2-D) Euler flows is provided. The stable tripole is composed of an inner elliptical vortex and two small-amplitude lateral vortices. The non-vanishing vorticity field of this tripole, referred to as here as an embedded tripole because of the closeness of its vortices, is given in elliptical coordinates 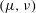 $(\unicode[STIX]{x1D707},\unicode[STIX]{x1D708})$ by the even radial and angular order-0 Mathieu functions
$(\unicode[STIX]{x1D707},\unicode[STIX]{x1D708})$ by the even radial and angular order-0 Mathieu functions 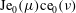 $\text{Je}_{0}(\unicode[STIX]{x1D707})\text{ce}_{0}(\unicode[STIX]{x1D708})$ truncated at the external branch of the vorticity isoline passing through the two critical points closest to the vortex centre. This tripole mode has a rigid vorticity field which rotates with constant angular velocity equal to
$\text{Je}_{0}(\unicode[STIX]{x1D707})\text{ce}_{0}(\unicode[STIX]{x1D708})$ truncated at the external branch of the vorticity isoline passing through the two critical points closest to the vortex centre. This tripole mode has a rigid vorticity field which rotates with constant angular velocity equal to 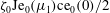 $\unicode[STIX]{x1D701}_{0}\text{Je}_{0}(\unicode[STIX]{x1D707}_{1})\text{ce}_{0}(0)/2$, where
$\unicode[STIX]{x1D701}_{0}\text{Je}_{0}(\unicode[STIX]{x1D707}_{1})\text{ce}_{0}(0)/2$, where 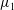 $\unicode[STIX]{x1D707}_{1}$ is the first zero of
$\unicode[STIX]{x1D707}_{1}$ is the first zero of 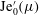 $\text{Je}_{0}^{\prime }(\unicode[STIX]{x1D707})$ and
$\text{Je}_{0}^{\prime }(\unicode[STIX]{x1D707})$ and 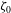 $\unicode[STIX]{x1D701}_{0}$ is a constant modal amplitude. It is argued that embedded 2-D tripoles may be conceptually regarded as the superposition of two asymmetric Chaplygin–Lamb dipoles, separated a distance equal to
$\unicode[STIX]{x1D701}_{0}$ is a constant modal amplitude. It is argued that embedded 2-D tripoles may be conceptually regarded as the superposition of two asymmetric Chaplygin–Lamb dipoles, separated a distance equal to 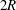 $2R$, as long as their individual trajectory curvature radius
$2R$, as long as their individual trajectory curvature radius 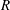 $R$ is much shorter than their dipole extent radius.
$R$ is much shorter than their dipole extent radius.
- Type
- JFM Rapids
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 2
- Cited by


