Hostname: page-component-848d4c4894-2xdlg Total loading time: 0 Render date: 2024-06-18T02:11:18.509Z Has data issue: false hasContentIssue false
  • English
  • Français

The role of soluble surfactants in the linear stability of two-layer flow in a channel

Published online by Cambridge University Press:  18 June 2019

A. Kalogirou Open the ORCID record for A. Kalogirou [Opens in a new window]  and
M. G. Blyth Open the ORCID record for M. G. Blyth [Opens in a new window]
A. Kalogirou*
Affiliation:
School of Mathematics, University of East Anglia, Norwich Research Park, Norwich NR4 7TJ, UK School of Mathematical Sciences, University of Nottingham, University Park, Nottingham NG7 2RD, UK
M. G. Blyth
Affiliation:
School of Mathematics, University of East Anglia, Norwich Research Park, Norwich NR4 7TJ, UK
*
†Email address for correspondence: Anna.Kalogirou@nottingham.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The linear stability of Couette–Poiseuille flow of two superposed fluid layers in a horizontal channel is considered. The lower fluid layer is populated with surfactants that appear either in the form of monomers or micelles and can also get adsorbed at the interface between the fluids. A mathematical model is formulated which combines the Navier–Stokes equations in each fluid layer, convection–diffusion equations for the concentration of monomers (at the interface and in the bulk fluid) and micelles (in the bulk), together with appropriate coupling conditions at the interface. The primary aim of this study is to investigate when the system is unstable to arbitrary wavelength perturbations, and in particular, to determine the influence of surfactant solubility and/or sorption kinetics on the instability. A linear stability analysis is performed and the growth rates are obtained by solving an eigenvalue problem for Stokes flow, both numerically for disturbances of arbitrary wavelength and analytically using long-wave approximations. It is found that the system is stable when the surfactant is sufficiently soluble in the bulk and if the fluid viscosity ratio 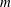$m$ and thickness ratio $n$ satisfy the condition $m<n^{2}$. On the other hand, the effect of surfactant solubility is found to be destabilising if 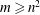$m\geqslant n^{2}$. Both of the aforementioned results are manifested for low bulk concentrations below the critical micelle concentration; however, when the equilibrium bulk concentration is sufficiently high (and above the critical micelle concentration) so that micelles are formed in the bulk fluid, the system is stable if 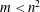$m<n^{2}$ in all cases examined.

JFM classification

Waves/Free-surface Flows: Channel flow Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 873 , 25 August 2019 , pp. 18 - 48
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bassom, A. P., Blyth, M. G. & Papageorgiou, D. T. 2010 Nonlinear development of two-layer Couette–Poiseuille flow in the presence of surfactant. Phys. Fluids 22 (102102), 1–15.10.1063/1.3488226Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Blyth, M. G. & Pozrikidis, C. 2004a Effect of inertia on the Marangoni instability of two-layer channel flow. Part II. Normal-mode analysis. J. Engng Maths 50, 329–341.10.1007/s10665-004-3691-zGoogle Scholar
Blyth, M. G. & Pozrikidis, C. 2004b Effect of surfactants on the stability of two-layer channel flow. J. Fluid Mech. 505, 59–86.10.1017/S0022112003007821Google Scholar
Boomkamp, P. A. M., Boersma, B. J., Miesen, R. H. M. & Beijnon, G. V. 1997 A Chebyshev collocation method for solving two-phase flow stability problems. J. Comput. Phys. 132, 191–200.10.1006/jcph.1996.5571Google Scholar
Booty, M. R. & Siegel, M. 2010 A hybrid numerical method for interfacial fluid flow with soluble surfactant. J. Comput. Phys. 229, 3864–3883.10.1016/j.jcp.2010.01.032Google Scholar
Breward, C. J. W. & Howell, P. D. 2004 Straining flow of a micellar surfactant solution. Euro. J. Appl. Maths 15, 511–531.10.1017/S0956792504005637Google Scholar
Burlatsky, S. F., Atrazhev, V. V., Dmitriev, D. V., Sultanov, V. I., Timokhina, E. N., Ugolkova, E. A., Tulyani, S. & Vincitore, A. 2013 Surface tension model for surfactant solutions at the critical micelle concentration. J. Colloid Interface Sci. 393, 151–160.10.1016/j.jcis.2012.10.020Google Scholar
Chang, C.-H. & Franses, E. I. 1995 Adsorption dynamics of surfactants at the air/water interface: a critical review of mathematical models, data, and mechanisms. Colloids Surf. A 100, 1–45.10.1016/0927-7757(94)03061-4Google Scholar
Craster, R. V. & Matar, O. K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81, 1131–1198.10.1103/RevModPhys.81.1131Google Scholar
Craster, R. V., Matar, O. K. & Papageorgiou, D. T. 2009 Breakup of surfactant-laden jets above the critical micelle concentration. J. Fluid Mech. 629, 195–219.10.1017/S0022112009006533Google Scholar
Danov, K. D., Vlahovska, P. M., Horozov, T., Dushkin, C. D., Kralchevsky, P. A., Mehreteab, A. & Broze, G. 1996 Adsorption from micellar surfactant solutions: nonlinear theory and experiment. J. Colloid Interface Sci. 183, 223–235.10.1006/jcis.1996.0537Google Scholar
De, S., Malik, S., Ghosh, A., Saha, R. & Saha, B. 2015 A review on natural surfactants. RSC Adv. 5, 65757.10.1039/C5RA11101CGoogle Scholar
Dongarra, J. J., Straughan, B. & Walker, D. W. 1996 Chebyshev tau-QZ algorithm methods for calculating spectra of hydrodynamic stability problems. Appl. Numer. Maths 22, 399–434.10.1016/S0168-9274(96)00049-9Google Scholar
Edmonstone, B. D., Craster, R. V. & Matar, O. K. 2006 Surfactant-induced fingering phenomena beyond the critical micelle concentration. J. Fluid Mech. 564, 105–138.10.1017/S0022112006001352Google Scholar
Elworthy, P. H. & Mysels, K. J. 1966 The surface tension of sodium dodecylsulfate solutions and the phase separation model of micelle formation. J. Colloid Interface Sci. 21, 331–347.10.1016/0095-8522(66)90017-1Google Scholar
Frenkel, A. L. & Halpern, D. 2002 Stokes-flow instability due to interfacial surfactant. Phys. Fluids 14 (7), 1–4.10.1063/1.1483838Google Scholar
Frenkel, A. L. & Halpern, D. 2006 Strongly nonlinear nature of interfacial-surfactant instability of Couette flow. Intl J. Pure Appl. Maths 29, 205–223.Google Scholar
Frenkel, A. L. & Halpern, D. 2017 Surfactant and gravity dependent instability of two-layer Couette flows and its nonlinear saturation. J. Fluid Mech. 826, 158–204.10.1017/jfm.2017.423Google Scholar
Frenkel, A. L., Halpern, D. & Schweiger, A. J. 2019a Surfactant- and gravity-dependent instability of two-layer channel flows: linear theory covering all wavelengths. Part 1. ‘Long-wave’ regimes. J. Fluid Mech. 863, 150–184.10.1017/jfm.2018.990Google Scholar
Frenkel, A. L., Halpern, D. & Schweiger, A. J. 2019b Surfactant- and gravity-dependent instability of two-layer channel flows: linear theory covering all wavelengths. Part 2. Mid-wave regimes. J. Fluid Mech. 863, 185–214.10.1017/jfm.2018.991Google Scholar
Georgantaki, A., Vlachogiannis, M. & Bontozoglou, V. 2012 The effect of soluble surfactants on liquid film flow. In 6th European Thermal Sciences Conference (Eurotherm 2012), 4–7 September 2012, Poitiers, France. IOP Publishing.Google Scholar
Georgantaki, A., Vlachogiannis, M. & Bontozoglou, V. 2016 Measurements of the stabilisation of liquid film flow by the soluble surfactant sodium dodecyl sulfate (SDS). Intl J. Multiphase Flow 86, 28–34.10.1016/j.ijmultiphaseflow.2016.07.011Google Scholar
Grotberg, J. B. 1994 Pulmonary flow and transport phenomena. Annu. Rev. Fluid Mech. 26, 529–571.10.1146/annurev.fl.26.010194.002525Google Scholar
Halpern, D. & Frenkel, A. L. 2003 Destabilization of a creeping flow by interfacial surfactant: linear theory extended to all wavenumbers. J. Fluid Mech. 485, 191–220.10.1017/S0022112003004476Google Scholar
Halpern, D. & Grotberg, J. B. 1992 Dynamics and transport of a localized soluble surfactant on a thin film. J. Fluid Mech. 237, 1–11.10.1017/S0022112092003318Google Scholar
Hashimoto, M., Garstecki, P., Stone, H. A. & Whitesides, G. M. 2008 Interfacial instabilities in a microfluidic Hele-Shaw cell. Soft Matt. 4, 1403–1413.Google Scholar
Hiemenz, P. C. & Rajagopalan, R. 1997 Principles of Colloid and Surface Chemistry. Marcel Dekker Inc.Google Scholar
Hooper, A. P. & Boyd, W. G. C. 1987 Shear-flow instability due to a wall and a viscosity discontinuity at the interface. J. Fluid Mech. 179, 201–225.10.1017/S0022112087001496Google Scholar
Jensen, O. E. & Grotberg, J. B. 1993 The spreading of heat or soluble surfactant along a thin liquid film. Phys. Fluids 5, 58–68.10.1063/1.858789Google Scholar
Ji, W. & Setterwall, F. 1994 On the instabilities of vertical falling liquid films in the presence of surface-active solute. J. Fluid Mech. 278, 291–323.10.1017/S0022112094003721Google Scholar
Kalogirou, A. 2018 Instability of two-layer film flows due to the interacting effects of surfactants, inertia and gravity. Phys. Fluids 30 (030707), 1–12.Google Scholar
Kalogirou, A. & Papageorgiou, D. T. 2016 Nonlinear dynamics of surfactant-laden two-fluid Couette flows in the presence of inertia. J. Fluid Mech. 802, 5–36.10.1017/jfm.2016.429Google Scholar
Karapetsas, G. & Bontozoglou, V. 2013 The primary instability of falling films in the presence of soluble surfactants. J. Fluid Mech. 729, 123–150.10.1017/jfm.2013.291Google Scholar
Karapetsas, G. & Bontozoglou, V. 2014 The role of surfactants on the mechanism of the long-wave instability in liquid film flows. J. Fluid Mech. 741, 139–155.10.1017/jfm.2013.670Google Scholar
Karapetsas, G., Matar, O. K. & Craster, R. V. 2011 On surfactant-enhanced spreading and superspreading of liquid drops on solid surfaces. J. Fluid Mech. 670, 5–37.10.1017/S0022112010005495Google Scholar
Liao, Y.-C., Basaran, O. A. & Franses, E. I. 2003 Micellar dissolution and diffusion effects on adsorption dynamics of surfactants. AIChE 49, 3229–3240.10.1002/aic.690491222Google Scholar
Matar, O. K. & Craster, R. V. 2009 Dynamics of surfactant-assisted spreading. Soft Matt. 5, 3801–3809.Google Scholar
Milliken, W. J., Stone, H. A. & Leal, L. G. 1993 The effect of surfactant on the transient motion of Newtonian drops. Phys. Fluids A 5, 69–79.10.1063/1.858790Google Scholar
Oron, A., Davis, S. H. & Bankoff, S. G. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69, 931–980.10.1103/RevModPhys.69.931Google Scholar
Orzag, S. A. 1971 Accurate solution of the Orr–Sommerfeld stability equation. J. Fluid Mech. 50, 659–703.Google Scholar
Pereira, A. & Kalliadasis, S. 2008 Dynamics of a falling film with solutal Marangoni effect. Phys. Rev. E 78 (036312), 1–19.Google Scholar
Picardo, J. R., Radhakrishna, T. G. & Pushpavanam, S. 2016 Solutal Marangoni instability in layered two-phase flows. J. Fluid Mech. 793, 280–315.10.1017/jfm.2016.135Google Scholar
Pozrikidis, C. 2004a Effect of inertia on the Marangoni instability of two-layer channel flow, Part I: numerical simulations. J. Engng Maths 50, 311–327.10.1007/s10665-004-3690-0Google Scholar
Pozrikidis, C. 2004b Instability of multi-layer channel and film flows. Adv. Appl. Mech. 40, 179–239.10.1016/S0065-2156(04)40002-7Google Scholar
Renardy, Y. Y. 1985 Instability at the interface between two shearing fluids in a channel. Phys. Fluids 28 (12), 3441–3443.10.1063/1.865346Google Scholar
Samanta, A. 2013 Effect of surfactant on two-layer channel flow. J. Fluid Mech. 735, 519–552.10.1017/jfm.2013.508Google Scholar
Shaw, D. J. 1992 Colloid and Surface Chemistry. Butterworth-Heinemann.Google Scholar
Shen, A. Q., Gleason, B., McKinley, G. H. & Stone, H. A. 2002 Fiber coating with surfactant solutions. Phys. Fluids 14 (11), 4055–4068.10.1063/1.1512287Google Scholar
Slattery, J. C. 1974 Interfacial effects in the entrapment and displacement of residual oil. AIChE J. 20, 1145–1154.10.1002/aic.690200613Google Scholar
Song, Q., Couzis, A., Somasundaran, P. & Maldarelli, C. 2006 A transport model for the adsorption of surfactant from micelle solutions onto a clean air/water interface in the limit of rapid aggregate disassembly relative to diffusion and supporting dynamic tension experiments. Colloids Surf. A 282–283, 162–182.Google Scholar
Stone, H. A. & Leal, L. G. 1990 The effects of surfactants on drop deformation and breakup. J. Fluid Mech. 220, 161–186.10.1017/S0022112090003226Google Scholar
Sun, Z. F. & Fahmy, M. 2006 Onset of Rayleigh–Benard–Marangoni convection in gas–liquid mass transfer with two-phase flow: Theory. Ind. Engng Chem. Res. 45, 3293–3302.10.1021/ie051185rGoogle Scholar
Wang, Q., Siegel, M. & Booty, M. R. 2014 Numerical simulation of drop and bubble dynamics with soluble surfactant. Phys. Fluids 26, 1–27.10.1063/1.4872174Google Scholar
Wei, H.-H. 2005 On the flow-induced Marangoni instability due to the presence of surfactant. J. Fluid Mech. 544, 173–200.10.1017/S0022112005006609Google Scholar
Weinstein, S. J. & Ruschak, K. J. 2004 Coating flows. Annu. Rev. Fluid Mech. 36, 29–53.10.1146/annurev.fluid.36.050802.122049Google Scholar
Wong, H., Rumschitzki, D. & Maldarelli, C. 1996 On the surfactant mass balance at a deforming fluid interface. Phys. Fluids 8, 3203–3204.10.1063/1.869098Google Scholar
Yiantsios, S. G. & Higgins, B. G. 1988 Linear stability of plane Poiseuille flow of two superposed fluids. Phys. Fluids 31 (11), 3225–3238.10.1063/1.866933Google Scholar
Yih, C.-H. 1967 Instability due to viscosity stratification. J. Fluid Mech. 27, 337–352.10.1017/S0022112067000357Google Scholar
You, X.-Y., Zhang, L.-D. & Zheng, J.-R. 2014 Marangoni instability of immiscible liquid–liquid stratified flow with a planar interface in the presence of interfacial mass transfer. J. Taiwan Inst. Chem. E 45, 772–779.10.1016/j.jtice.2013.08.007Google Scholar
Zaisha, M., Ping, L., Guangji, Z. & Chao, Y. 2008 Numerical simulation of the Marangoni effect with interphase mass transfer between two planar liquid layers. Chinese J. Chem. Eng. 16, 161–170.Google Scholar
Zhmud, B. V., Tiberg, F. & Kizling, J. 2000 Dynamic surface tension in concentrated solutions of C n E m surfactants: a comparison between the theory and experiment. Langmuir 16, 2557–2565.10.1021/la991144yGoogle Scholar