Article contents
Long frontal waves and dynamic scaling in freely evolving equivalent barotropic flow
Published online by Cambridge University Press: 18 March 2019
Abstract
We present a scaling theory that links the frequency of long frontal waves to the kinetic energy decay rate and inverse transfer of potential energy in freely evolving equivalent barotropic turbulence. The flow energy is predominantly potential, and the streamfunction makes the dominant contribution to potential vorticity (PV) over most of the domain, except near PV fronts of width  $O(L_{D})$, where
$O(L_{D})$, where 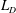 $L_{D}$ is the Rossby deformation length. These fronts bound large vortices within which PV is well-mixed and arranged into a staircase structure. The jets collocated with the fronts support long-wave undulations, which facilitate collisions and mergers between the mixed regions, implicating the frontal dynamics in the growth of potential-energy-containing flow features. Assuming the mixed regions grow self-similarly in time and using the dispersion relation for long frontal waves (Nycander et al., Phys. Fluids A, vol. 5, 1993, pp. 1089–1091) we predict that the total frontal length and kinetic energy decay like
$L_{D}$ is the Rossby deformation length. These fronts bound large vortices within which PV is well-mixed and arranged into a staircase structure. The jets collocated with the fronts support long-wave undulations, which facilitate collisions and mergers between the mixed regions, implicating the frontal dynamics in the growth of potential-energy-containing flow features. Assuming the mixed regions grow self-similarly in time and using the dispersion relation for long frontal waves (Nycander et al., Phys. Fluids A, vol. 5, 1993, pp. 1089–1091) we predict that the total frontal length and kinetic energy decay like 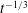 $t^{-1/3}$, while the length scale of the staircase vortices grows like
$t^{-1/3}$, while the length scale of the staircase vortices grows like 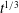 $t^{1/3}$. High-resolution simulations confirm our predictions.
$t^{1/3}$. High-resolution simulations confirm our predictions.
- Type
- JFM Rapids
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 3
- Cited by


