Article contents
Interface-resolved numerical simulations of particle-laden turbulent flows in a vertical channel filled with Bingham fluids
Published online by Cambridge University Press: 28 November 2019
Abstract
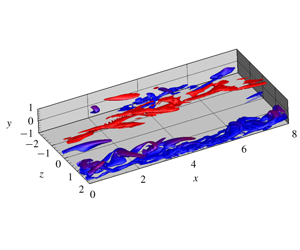
In this paper, a fictitious domain method is used to perform interface-resolved numerical simulations of particle-laden turbulent flows in a vertical channel filled with Bingham fluids. The interactions between the particles and the turbulence are investigated at a bulk Reynolds number of 8000 (based on the mean velocity and the channel width), a particle/channel size ratio of 0.1 and a particle volume fraction of 2 %. The Bingham number based on the mean velocity and the channel half-width is 0.0, 0.54 and 3.0, respectively. Both neutrally buoyant and weak particle settling effects are considered. Our results indicate that the yield stress of Bingham fluids has drag-reduction effects by weakening the turbulence, and the addition of the particles enhances the flow friction. The Saffman lift force is important to the particle concentration distribution across the channel. Particle sedimentation attenuates the fluctuating velocity and Reynolds stress, resulting in a smaller flow friction compared with the neutrally buoyant case. When the fluid plasticity is strong, the single-phase flow has considerable temporal and spatial intermittencies. The vortex structures in one half-channel can be stronger than those in the other half-channel for a long period, resulting in the asymmetry of the statistics for a long time. The vortices are preferentially concentrated in streamwise-extended bands. The vortex bands and the laminar flow regions are largely segregated in the spanwise directions, and the vortex bands in the two half-channels are also typically staggered in the spanwise direction. The addition of the particles suppresses such vortex structures, the enormous intermittency and the asymmetry during the transition in the single-phase flow.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 16
- Cited by


