Hostname: page-component-594f858ff7-hf9kg Total loading time: 0 Render date: 2023-06-10T05:22:44.369Z Has data issue: false Feature Flags: { "corePageComponentGetUserInfoFromSharedSession": true, "coreDisableEcommerce": false, "corePageComponentUseShareaholicInsteadOfAddThis": true, "coreDisableSocialShare": false, "useRatesEcommerce": true } hasContentIssue false
  • English

Instability and transition of a vertical ascension or fall of a free sphere affected by a vertical magnetic field

Published online by Cambridge University Press:  16 November 2018

Jun-Hua Pan ,
Nian-Mei Zhang  and
Ming-Jiu Ni Open the ORCID record for Ming-Jiu Ni[Opens in a new window]
Jun-Hua Pan
Affiliation:
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, China
Nian-Mei Zhang
Affiliation:
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, China
Ming-Jiu Ni*
Affiliation:
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, China
*
†Email address for correspondence: mjni@ucas.ac.cn
Get access Rights & Permissions[Opens in a new window]

Abstract

When the Galileo number is below the first bifurcation, the instability and transition of a vertical ascension or the fall of a free sphere affected by a vertical magnetic field are investigated numerically. A compact model is used to explain that the magnetic field can destabilize the fluid–solid system. When the interaction parameter exceeds a critical value, the sphere trajectory is transitioned from a steady vertical trajectory to a steady oblique one. Furthermore, the trajectory will remain vertical at a sufficiently large magnetic field because of a double effect of the magnetic field on the fluid–solid system. Under the influence of an external vertical magnetic field, four wake patterns at the rear of the sphere are found and the physical behaviour of the free sphere is independent of the density ratio. The wake or trajectory of the free sphere is only determined by the Galileo number 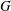$G$ and the interaction parameter 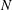$N$. A close relationship between the streamwise vorticity and the sphere motion is found. An interesting ‘agglomeration phenomenon’ is also found, which shows that the vertical velocities are agglomerated into a point for a certain magnetic field regardless of the Galileo number and satisfy a scaling law 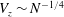$V_{z}\sim N^{-1/4}$, when $N>1$. The principal results of the present work are summarized in a map of regimes in the 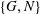$\{G,N\}$ plane.

JFM classification

Materials Processing Flows: Materials Processing Flows Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 859 , 25 January 2019 , pp. 33 - 48
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cuevas, S., Smolentsev, S. & Abdou, M. A. 2006 On the flow past a magnetic obstacle. J. Fluid Mech. 553, 227–252.CrossRefGoogle Scholar
Davidson, P. A. 2001 An Introduction to Magnetohydrodynamics. Cambridge University Press.CrossRefGoogle Scholar
Dullweber, A., Leimkuhler, B. & McLachlan, R. 1997 Symplectic splitting methods for rigid body molecular dynamics. J. Chem. Phys. 107 (15), 5840–5851.CrossRefGoogle Scholar
El-Kaddah, N., Patel, A. D. & Natarajan, T. T. 1995 The electromagnetic filtration of molten aluminum using an induced-current separator. JOM J. Miner. Met. Mater. Soc. 47 (5), 46–49.CrossRefGoogle Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.CrossRefGoogle Scholar
Fabre, D., Tchoufag, J. & Magnaudet, J. 2012 The steady oblique path of buoyancy-driven disks and spheres. J. Fluid Mech. 707, 24–36.CrossRefGoogle Scholar
Giacobello, M., Ooi, A. & Balachandar, S. 2009 Wake structure of a transversely rotating sphere at moderate Reynolds numbers. J. Fluid Mech. 621, 103–130.CrossRefGoogle Scholar
Goldsworthy, F. A. 1961 Magnetohydrodynamic flows of a perfectly conducting, viscous fluid. J. Fluid Mech. 11 (4), 519–528.CrossRefGoogle Scholar
Horowitz, M. & Williamson, C. H. K. 2010 The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.CrossRefGoogle Scholar
Hu, H. H., Patankar, N. A. & Zhu, M. Y. 2001 Direct numerical simulations of fluid–solid systems using the arbitrary Lagrangian–Eulerian technique. J. Comput. Phys. 169 (2), 427–462.CrossRefGoogle Scholar
Jenny, M., Bouchet, G. & Dušek, J. 2003 Nonvertical ascension or fall of a free sphere in a Newtonian fluid. Phys. Fluids 15 (1), L9–L12.CrossRefGoogle Scholar
Jenny, M. & Dušek, J. 2004 Efficient numerical method for the direct numerical simulation of the flow past a single light moving spherical body in transitional regimes. J. Comput. Phys. 194 (1), 215–232.CrossRefGoogle Scholar
Jenny, M., Dušek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.CrossRefGoogle Scholar
Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.CrossRefGoogle Scholar
Kanaris, N., Albets, X., Grigoriadis, D. & Kassinos, S. 2013 Three-dimensional numerical simulations of magnetohydrodynamic flow around a confined circular cylinder under low, moderate, and strong magnetic fields. Phys. Fluids 25 (7), 074102.CrossRefGoogle Scholar
Lahjomri, J., Capéran, P. & Alemany, A. 1993 The cylinder wake in a magnetic field aligned with the velocity. J. Fluid Mech. 253, 421–448.CrossRefGoogle Scholar
Lighthill, M. J. 1963 Boundary layer theory. In Laminar Boundary Layers (ed. Rosenhead, L.), pp. 46–113. Oxford University Press.Google Scholar
Mathai, V., Zhu, X., Sun, C. & Lohse, D. 2017 Mass and moment of inertia govern the transition in the dynamics and wakes of freely rising and falling cylinders. Phys. Rev. Lett. 119 (5), 054501.CrossRefGoogle ScholarPubMed
Mathai, V., Zhu, X., Sun, C. & Lohse, D. 2018 Flutter to tumble transition of buoyant spheres triggered by rotational inertia changes. Nat. Commun. 9 (1), 1792.CrossRefGoogle ScholarPubMed
Moreau, R. J. 2013 Magnetohydrodynamics. Springer Science & Business Media.Google Scholar
Mück, B., Günther, C., Müller, U. & Bühler, L. 2000 Three-dimensional MHD flows in rectangular ducts with internal obstacles. J. Fluid Mech. 418, 265–295.CrossRefGoogle Scholar
Mutschke, G., Gerbeth, G., Shatrov, V. & Tomboulides, A. 2001 The scenario of three-dimensional instabilities of the cylinder wake in an external magnetic field: a linear stability analysis. Phys. Fluids 13 (3), 723–734.CrossRefGoogle Scholar
Ni, M.-J., Munipalli, R., Huang, P., Morley, N. B. & Abdou, M. A. 2007 A current density conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. Part II. On an arbitrary collocated mesh. J. Comput. Phys. 227 (1), 205–228.CrossRefGoogle Scholar
Pan, J.-H., Zhang, N.-M. & Ni, M.-J. 2018 The wake structure and transition process of a flow past a sphere affected by a streamwise magnetic field. J. Fluid Mech. 842, 248–272.CrossRefGoogle Scholar
Schwarz, S., Kempe, T. & Fröhlich, J. 2015 A temporal discretization scheme to compute the motion of light particles in viscous flows by an immersed boundary method. J. Comput. Phys. 281, 591–613.CrossRefGoogle Scholar
Tchoufag, J., Fabre, D. & Magnaudet, J. 2014 Global linear stability analysis of the wake and path of buoyancy-driven disks and thin cylinders. J. Fluid Mech. 740, 278–311.CrossRefGoogle Scholar
Veldhuis, C. H. J. & Biesheuvel, A. 2007 An experimental study of the regimes of motion of spheres falling or ascending freely in a Newtonian fluid. Intl J. Multiphase Flow 33 (10), 1074–1087.CrossRefGoogle Scholar
Yonas, G. 1967 Measurements of drag in a conducting fluid with an aligned field and large interaction parameter. J. Fluid Mech. 30 (4), 813–821.CrossRefGoogle Scholar
Zhang, C., Eckert, S. & Gerbeth, G. 2005 Experimental study of single bubble motion in a liquid metal column exposed to a DC magnetic field. Intl J. Multiphase Flow 31 (7), 824–842.CrossRefGoogle Scholar
Zhang, J. & Ni, M.-J. 2017 What happens to the vortex structures when the rising bubble transits from zigzag to spiral? J. Fluid Mech. 828, 353–373.CrossRefGoogle Scholar
Zheng, T. X., Zhong, Y. B., Lei, Z. S., Ren, W. L., Ren, Z. M., Debray, F., Beaugnon, E. & Fautrelle, Y. 2015 Effects of high static magnetic field on distribution of solid particles in BiZn immiscible alloys with metastable miscibility gap. J. Alloys Compounds 623, 36–41.CrossRefGoogle Scholar
Zhou, W. & Dušek, J. 2015 Chaotic states and order in the chaos of the paths of freely falling and ascending spheres. Intl J. Multiphase Flow 75, 205–223.CrossRefGoogle Scholar