Article contents
Hydrodynamics of swimming in stingrays: numerical simulations and the role of the leading-edge vortex
Published online by Cambridge University Press: 05 January 2016
Abstract
Stingrays, in contrast with many other aquatic animals, have flattened disk-shaped bodies with expanded pectoral ‘wings’, which are used for locomotion in water. To discover the key features of stingray locomotion, large-eddy simulations of a self-propelled stingray, modelled closely after the freshwater stingray, Potamotrygon orbignyi, are performed. The stingray’s body motion was prescribed based on three-dimensional experimental measurement of wing and body kinematics in live stingrays at two different swimming speeds of 1.5 and 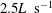 $2.5L~\text{s}^{-1}$ (
$2.5L~\text{s}^{-1}$ (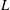 $L$ is the disk length of the stingray). The swimming speeds predicted by the self-propelled simulations were within 12 % of the nominal swimming speeds in the experiments. It was found that the fast-swimming stingray (Reynolds number
$L$ is the disk length of the stingray). The swimming speeds predicted by the self-propelled simulations were within 12 % of the nominal swimming speeds in the experiments. It was found that the fast-swimming stingray (Reynolds number 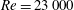 $Re=23\,000$ and Strouhal number
$Re=23\,000$ and Strouhal number 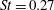 $St=0.27$) is approximately 12 % more efficient than the slow-swimming one (
$St=0.27$) is approximately 12 % more efficient than the slow-swimming one (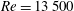 $Re=13\,500$,
$Re=13\,500$, 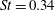 $St=0.34$). This is related to the wake of the fast- and slow-swimming stingrays, which was visualized along with the pressure on the stingray’s body. A horseshoe vortex was discovered to be present at the anterior margin of the stingray, creating a low-pressure region that enhances thrust for both fast and slow swimming speeds. Furthermore, it was found that a leading-edge vortex (LEV) on the pectoral disk of swimming stingrays generates a low-pressure region in the fast-swimming stingray, whereas the low- and high-pressure regions in the slow-swimming one are in the back half of the wing and not close to any vortical structures. The undulatory motion creates thrust by accelerating the adjacent fluid (the added-mass mechanism), which is maximized in the back of the wing because of higher undulations and velocities in the back. However, the thrust enhancement by the LEV occurs in the front portion of the wing. By computing the forces on the front half and the back half of the wing, it was found that the contribution of the back half of the wing to thrust in a slow-swimming stingray is several-fold higher than in the fast-swimming one. This indicates that the LEV enhances thrust in fast-swimming stingrays and improves the efficiency of swimming.
$St=0.34$). This is related to the wake of the fast- and slow-swimming stingrays, which was visualized along with the pressure on the stingray’s body. A horseshoe vortex was discovered to be present at the anterior margin of the stingray, creating a low-pressure region that enhances thrust for both fast and slow swimming speeds. Furthermore, it was found that a leading-edge vortex (LEV) on the pectoral disk of swimming stingrays generates a low-pressure region in the fast-swimming stingray, whereas the low- and high-pressure regions in the slow-swimming one are in the back half of the wing and not close to any vortical structures. The undulatory motion creates thrust by accelerating the adjacent fluid (the added-mass mechanism), which is maximized in the back of the wing because of higher undulations and velocities in the back. However, the thrust enhancement by the LEV occurs in the front portion of the wing. By computing the forces on the front half and the back half of the wing, it was found that the contribution of the back half of the wing to thrust in a slow-swimming stingray is several-fold higher than in the fast-swimming one. This indicates that the LEV enhances thrust in fast-swimming stingrays and improves the efficiency of swimming.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 100
- Cited by



