Article contents
Heat flux correlation for high-speed flow in the transitional regime
Published online by Cambridge University Press: 08 March 2016
Abstract
An analytical correlation is developed for stagnation-point heat flux on spherical objects travelling at high velocity which is accurate for conditions ranging from the continuum to the free-molecular flow regime. Theoretical analysis of the Burnett and super-Burnett equations is performed using simplifications from shock-wave and boundary-layer theory to determine the relative contribution of higher-order heat flux terms compared with the Fourier heat flux (assumed in the Navier–Stokes equations). A rarefaction parameter (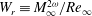 $W_{r}\equiv M_{\infty }^{2{\it\omega}}/Re_{\infty }$), based on the free-stream Mach number (
$W_{r}\equiv M_{\infty }^{2{\it\omega}}/Re_{\infty }$), based on the free-stream Mach number (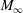 $M_{\infty }$), the Reynolds number (
$M_{\infty }$), the Reynolds number (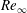 $Re_{\infty }$) and the viscosity–temperature index (
$Re_{\infty }$) and the viscosity–temperature index (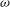 ${\it\omega}$), is identified as a better correlating parameter than the Knudsen number in the transition regime. By studying both the Burnett and super-Burnett equations, a general form for the entire series of higher-order heat flux contributions is obtained. The resulting heat flux expression includes terms with dependence on gas properties, stagnation to wall-temperature ratio and a main dependence on powers of the rarefaction parameter
${\it\omega}$), is identified as a better correlating parameter than the Knudsen number in the transition regime. By studying both the Burnett and super-Burnett equations, a general form for the entire series of higher-order heat flux contributions is obtained. The resulting heat flux expression includes terms with dependence on gas properties, stagnation to wall-temperature ratio and a main dependence on powers of the rarefaction parameter 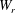 $W_{r}$. The expression is applied as a correction to the Fourier heat flux and therefore can be combined with any continuum-based correlation of choice. In the free-molecular limit, a bridging function is used to ensure consistency with well-established free-molecular flow theory. The correlation is then fitted to direct simulation Monte Carlo (DSMC) solutions for stagnation-point heat flux in high-speed nitrogen flows. The correlation is shown to accurately capture the variation in heat flux predicted by the DSMC method in the transition flow regime, while limiting to both continuum and free-molecular values.
$W_{r}$. The expression is applied as a correction to the Fourier heat flux and therefore can be combined with any continuum-based correlation of choice. In the free-molecular limit, a bridging function is used to ensure consistency with well-established free-molecular flow theory. The correlation is then fitted to direct simulation Monte Carlo (DSMC) solutions for stagnation-point heat flux in high-speed nitrogen flows. The correlation is shown to accurately capture the variation in heat flux predicted by the DSMC method in the transition flow regime, while limiting to both continuum and free-molecular values.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 19
- Cited by



