Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-01T21:31:30.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Forward flight and sideslip manoeuvre of a model hawkmoth

Published online by Cambridge University Press:  04 June 2020

Jie Yao Open the ORCID record for Jie Yao [Opens in a new window]  and
K. S. Yeo
Jie Yao
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 9 Engineering Drive 1, Singapore117576, Republic of Singapore
K. S. Yeo*
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 9 Engineering Drive 1, Singapore117576, Republic of Singapore
*
†Email addresses for correspondence: mpeyeoks@nus.edu.sg, mpeyeoks@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

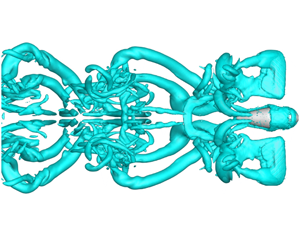
This paper presents a computational study on the free forward flight and sideslip manoeuvre of an insect-like flapping-wing flyer modelled after the hummingbird hawkmoth (Macroglossum stellatarum), with Reynolds number ${\sim}3000$. The numerical model integrated a Navier–Stokes fluid solver with the Newtonian free-body dynamics of the flyer. A generic proportional–integral–derivative (PID)-based wing kinematics controller was used to achieve stable controlled flight. State-equation analyses of flight dynamics were helpful in identifying the roles of kinematic wing actions and for establishing control coefficients for stable flight. Forward flights up to a speed of $4.3~\text{m}~\text{s}^{-1}$ were simulated, which show that the wingbeat frequency decreased below the hovering frequency for cruising flight in the low- and medium-speed range, and higher frequency was only needed for high-speed flight. Similarly, the aerodynamic power consumption was also lower than that for hovering flight over the simulated speed range, due to the contribution of wing drag to overall lift. In addition, flight with higher speed tends to be more efficient in terms of energy consumption for the same distance travelled. In a complete sideslip manoeuvre, the model hawkmoth took approximately 20 wing cycles to translate laterally 4.5 wing lengths to its right and another 30 wing cycles to stabilize hovering at the new location. Slightly higher wingbeat frequency and power were required during the sideslipping phase to adjust for drop in lift due to body roll. The evolution of the vortical wakes reflects quite well the major mechanisms of force generation that were at play at key stages in these flights.

JFM classification

Biological Fluid Dynamics: Swimming/flying
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 896 , 10 August 2020 , A22
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altshuler, D. L., Dickson, W. B., Vance, J. T., Roberts, S. P. & Dickinson, M. H. 2005 Short-amplitude high-frequency wing strokes determine the aerodynamics of honeybee flight. Proc. Natl Acad. Sci. USA 102 (50), 18213–18218.CrossRefGoogle ScholarPubMed
Aono, H., Liang, F. & Liu, H. 2008 Near-and far-field aerodynamics in insect hovering flight: an integrated computational study. J. Expl Biol. 211 (2), 239–257.CrossRefGoogle Scholar
Birch, J. M. & Dickinson, M. H. 2001 Spanwise flow and the attachment of the leading-edge vortex on insect wings. Nature 412 (6848), 729–733.CrossRefGoogle Scholar
Birch, J. M., Dickson, W. B. & Dickinson, M. H. 2004 Force production and flow structure of the leading edge vortex on flapping wings at high and low Reynolds numbers. J. Expl Biol. 207 (7), 1063–1072.CrossRefGoogle Scholar
Brodsky, A. 1991 Vortex formation in the tethered flight of the peacock butterfly Inachis io L. (Lepidoptera, Nymphalidae) and some aspects of insect flight evolution. J. Expl Biol. 161 (1), 77–95.Google Scholar
Chew, C. S., Yeo, K. S. & Shu, C. 2006 A generalized finite-difference (GFD) ALE scheme for incompressible flows around moving solid bodies on hybrid meshfree–Cartesian grids. J. Comput. Phys. 218 (2), 510–548.CrossRefGoogle Scholar
Cooter, R. & Baker, P. 1977 Weis-Fogh clap and fling mechanism in Locusta. Nature 269 (5623), 53–54.CrossRefGoogle Scholar
Dickens, M. 1974 The World of Moths. Osprey.Google Scholar
Dickinson, M. H. 1994 The effects of wing rotation on unsteady aerodynamic performance at low Reynolds numbers. J. Expl Biol. 192 (1), 179–206.Google ScholarPubMed
Dickinson, M. H., Lehmann, F.-O. & Sane, S. P. 1999 Wing rotation and the aerodynamic basis of insect flight. Science 284 (5422), 1954–1960.CrossRefGoogle ScholarPubMed
Dudley, R. & Ellington, C. 1990a Mechanics of forward flight in bumblebees: I. Kinematics and morphology. J. Expl Biol. 148 (1), 19–52.Google Scholar
Dudley, R. & Ellington, C. 1990b Mechanics of forward flight in bumblebees: II. Quasi-steady lift and power requirements. J. Expl Biol. 148 (1), 53–88.Google Scholar
Ellington, C. 1984a The aerodynamics of hovering insect flight. I. The quasi-steady analysis. Phil. Trans. R. Soc. Lond. B 305 (1122), 1–15.Google Scholar
Ellington, C. 1984b The aerodynamics of hovering insect flight. III. Kinematics. Phil. Trans. R. Soc. Lond. B 305 (1122), 41–78.Google Scholar
Ellington, C. P., Van Den Berg, C., Willmott, A. P. & Thomas, A. L. 1996 Leading-edge vortices in insect flight. Nature 384 (6610), 626–630.CrossRefGoogle Scholar
Fry, S. N., Sayaman, R. & Dickinson, M. H. 2003 The aerodynamics of free-flight maneuvers in Drosophila. Science 300 (5618), 495–498.CrossRefGoogle ScholarPubMed
Fry, S. N., Sayaman, R. & Dickinson, M. H. 2005 The aerodynamics of hovering flight in Drosophila. J. Expl Biol. 208 (12), 2303–2318.CrossRefGoogle ScholarPubMed
Gilmanov, A. & Sotiropoulos, F. 2005 A hybrid Cartesian/immersed boundary method for simulating flows with 3D, geometrically complex, moving bodies. J. Comput. Phys. 207 (2), 457–492.CrossRefGoogle Scholar
Greeter, J. S. & Hedrick, T. L. 2016 Direct lateral maneuvers in hawkmoths. Biology Open 5 (1), 72–82.CrossRefGoogle ScholarPubMed
Hedrick, T. L. & Daniel, T. 2006 Flight control in the hawkmoth Manduca sexta: the inverse problem of hovering. J. Expl Biol. 209 (16), 3114–3130.CrossRefGoogle ScholarPubMed
Houghton, E. L. & Carpenter, P. W. 2003 Aerodynamics for Engineering Students. Butterworth-Heinemann.Google Scholar
Johansson, L. C., Engel, S., Kelber, A., Heerenbrink, M. K. & Hedenström, A. 2013 Multiple leading edge vortices of unexpected strength in freely flying hawkmoth. Sci. Rep. 3, 3264.CrossRefGoogle ScholarPubMed
Liu, G., Dong, H. & Li, C. 2016 Vortex dynamics and new lift enhancement mechanism of wing–body interaction in insect forward flight. J. Fluid Mech. 795, 634–651.CrossRefGoogle Scholar
Liu, H. 2009 Integrated modeling of insect flight: from morphology, kinematics to aerodynamics. J. Comput. Phys. 228 (2), 439–459.CrossRefGoogle Scholar
Liu, H., Ellington, C. P., Kawachi, K., Van Den Berg, C. & Willmott, A. P. 1998 A computational fluid dynamic study of hawkmoth hovering. J. Expl Biol. 201 (4), 461–477.Google ScholarPubMed
Liu, H. & Kawachi, K. 1998 A numerical study of insect flight. J. Comput. Phys. 146 (1), 124–156.CrossRefGoogle Scholar
Lua, K., Lee, Y., Lim, T. & Yeo, K. S. 2016 Aerodynamic effects of elevating motion on hovering rigid hawkmothlike wings. AIAA J. (0), 2247–2264.CrossRefGoogle Scholar
Miller, L. A. & Peskin, C. S. 2005 A computational fluid dynamics of clap and fling’ in the smallest insects. J. Expl Biol. 208 (2), 195–212.CrossRefGoogle ScholarPubMed
Miller, L. A. & Peskin, C. S. 2009 Flexible clap and fling in tiny insect flight. J. Expl Biol. 212 (19), 3076–3090.CrossRefGoogle ScholarPubMed
Mordant, N. & Pinton, J.-F. 2000 Velocity measurement of a settling sphere. Eur. Phys. J. B 18 (2), 343–352.CrossRefGoogle Scholar
Muijres, F., Johansson, L. C., Barfield, R., Wolf, M., Spedding, G. & Hedenström, A. 2008 Leading-edge vortex improves lift in slow-flying bats. Science 319 (5867), 1250–1253.CrossRefGoogle ScholarPubMed
Nakata, T. & Liu, H. 2012a Aerodynamic performance of a hovering hawkmoth with flexible wings: a computational approach. Proc. R. Soc. Lond. B 279 (1729), 722–731.CrossRefGoogle Scholar
Nakata, T. & Liu, H. 2012b A fluid–structure interaction model of insect flight with flexible wings. J. Comput. Phys. 231 (4), 1822–1847.CrossRefGoogle Scholar
Nguyen, T., Sundar, D. S., Yeo, K. S. & Lim, T. T. 2016 Modeling and analysis of insect-like flexible wings at low Reynolds number. J. Fluids Struct. 62, 294–317.CrossRefGoogle Scholar
Osborne, M. 1951 Aerodynamics of flapping flight with application to insects. J. Expl Biol. 28 (2), 221–245.Google ScholarPubMed
Pennycuick, C. 1975 Mechanics of flight. Avian Biol. 5, 1–73.Google Scholar
Ramamurti, R. & Sandberg, W. C. 2002 A three-dimensional computational study of the aerodynamic mechanisms of insect flight. J. Expl Biol. 205 (10), 1507–1518.Google ScholarPubMed
Shyy, W., Aono, H., Chimakurthi, S. K., Trizila, P., Kang, C.-K., Cesnik, C. E. & Liu, H. 2010 Recent progress in flapping wing aerodynamics and aeroelasticity. Progr. Aerosp. Sci. 46 (7), 284–327.CrossRefGoogle Scholar
Shyy, W., Aono, H., Kang, C. & Liu, H. 2013 An Introduction to Flapping Wing Aerodynamics. Cambridge University Press.CrossRefGoogle Scholar
Shyy, W., Lian, Y., Tang, J., Viieru, D. & Liu, H. 2007 Aerodynamics of Low Reynolds Number Flyers, vol. 22. Cambridge University Press.Google Scholar
Srygley, R. & Thomas, A. 2002 Unconventional lift-generating mechanisms in free-flying butterflies. Nature 420 (6916), 660–664.CrossRefGoogle ScholarPubMed
Stevenson, R., Corbo, K., Baca, L. & Le, Q. 1995 Cage size and flight speed of the tobacco hawkmoth Manduca sexta. J. Expl Biol. 198 (8), 1665–1672.Google ScholarPubMed
Sun, M. & Tang, J. 2002 Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion. J. Expl Biol. 205 (1), 55–70.Google ScholarPubMed
Sun, M., Wang, J. & Xiong, Y. 2007 Dynamic flight stability of hovering insects. Acta Mech. Sin. 23 (3), 231–246.CrossRefGoogle Scholar
Sun, M. & Xiong, Y. 2005 Dynamic flight stability of a hovering bumblebee. J. Expl Biol. 208 (3), 447–459.CrossRefGoogle ScholarPubMed
Tang, J., Viieru, D. & Shyy, W. 2008 Effects of Reynolds number and flapping kinematics on hovering aerodynamics. AIAA J. 46 (4), 967–976.CrossRefGoogle Scholar
Taylor, G. K. & Thomas, A. L. 2003 Dynamic flight stability in the desert locust Schistocerca gregaria. J. Expl Biol. 206 (16), 2803–2829.CrossRefGoogle ScholarPubMed
Wang, X. Y., Yeo, K. S., Chew, C. S. & Khoo, B. C. 2008 A SVD-GFD scheme for computing 3D incompressible viscous fluid flows. Comput. Fluids 37 (6), 733–746.CrossRefGoogle Scholar
Wang, X. Y., Yu, P., Yeo, K. S. & Khoo, B. C. 2010 SVD-GFD scheme to simulate complex moving body problems in 3D space. J. Comput. Phys. 229 (6), 2314–2338.CrossRefGoogle Scholar
Wang, Z. J. 2000 Two dimensional mechanism for insect hovering. Phys. Rev. Lett. 85 (10), 2216.CrossRefGoogle Scholar
Warfvinge, K., Kleinheerenbrink, M. & Hedenström, A. 2017 The power–speed relationship is U-shaped in two free-flying hawkmoths (Manduca sexta). J. R. Soc. Interface 14 (134), 20170372.CrossRefGoogle Scholar
Weis-Fogh, T. 1972 Energetics of hovering flight in hummingbirds and in Drosophila. J. Expl Biol. 56 (1), 79–104.Google Scholar
Weis-Fogh, T. 1973 Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production. J. Expl Biol. 59 (1), 169–230.Google Scholar
Weis-Fogh, T. & Jensen, M. 1956 Biology and physics of locust flight. I. Basic principles in insect flight. A critical review. Phil. Trans. R. Soc. Lond. B 239 (667), 415–458.Google Scholar
Willmott, A. P. & Ellington, C. P. 1997a The mechanics of flight in the hawkmoth Manduca sexta. I. Kinematics of hovering and forward flight. J. Expl Biol. 200 (21), 2705–2722.Google Scholar
Willmott, A. P. & Ellington, C. P. 1997b The mechanics of flight in the hawkmoth Manduca sexta. II. Aerodynamic consequences of kinematic and morphological variation. J. Expl Biol. 200 (21), 2723–2745.Google Scholar
Willmott, A. P., Ellington, C. P. & Thomas, A. L. 1997 Flow visualization and unsteady aerodynamics in the flight of the hawkmoth, Manduca sexta. Phil. Trans. R. Soc. Lond. B 352 (1351), 303–316.CrossRefGoogle Scholar
Wootton, R. J. & Newman, D. J. 1979 Whitefly have the highest contraction frequencies yet recorded in non-fibrillar flight muscles. Nature 280 (5721), 402–403.CrossRefGoogle Scholar
Wu, D., Yeo, K. S. & Lim, T. T. 2014 A numerical study on the free hovering flight of a model insect at low Reynolds number. Comput. Fluids 103, 234–261.CrossRefGoogle Scholar
Wu, G. & Zeng, L. 2010 Measuring the kinematics of a free-flying hawk-moth (Macroglossum stellatarum) by a comb-fringe projection method. Acta Mech. Sin. 26 (1), 67–71.CrossRefGoogle Scholar
Wu, J. H. & Sun, M. 2012 Floquet stability analysis of the longitudinal dynamics of two hovering model insects. J. R. Soc. Interface 9 (74), 2033–2046.CrossRefGoogle ScholarPubMed
Wu, J. H., Zhang, Y. L. & Sun, M. 2009 Hovering of model insects: simulation by coupling equations of motion with Navier–Stokes equations. J. Expl Biol. 212 (20), 3313–3329.CrossRefGoogle ScholarPubMed
Xiong, Y. & Sun, M. 2008 Dynamic flight stability of a bumblebee in forward flight. Acta Mech. Sin. 24 (1), 25–36.CrossRefGoogle Scholar
Yao, J.2018 Computational aerodynamics of hawkmoth free flight. Doctoral dissertation, National University of Singapore.Google Scholar
Yao, J. & Yeo, K. S. 2019a Free hovering of hummingbird hawkmoth and effects of wing mass and wing elevation. Comput. Fluids 186, 99–127.CrossRefGoogle Scholar
Yao, J. & Yeo, K. S. 2019b A simplified dynamic model for controlled insect hovering flight and control stability analysis. Bioinspir. Biomimet. 14 (5), 056005.CrossRefGoogle Scholar
Yao, Y. & Yeo, K. S. 2018 Longitudinal free flight of a model insect flyer at low Reynolds number. Comput. Fluids 162, 72–90.CrossRefGoogle Scholar
Yao, Y. & Yeo, K. S. 2019c Manoeuvring flight of a model insect – saccadic yaw and sideslip. Comput. Fluids 180, 54–67.CrossRefGoogle Scholar
Yeo, K. S., Ang, S. J. & Shu, C. 2010 Simulation of fish swimming and manoeuvring by an SVD-GFD method on a hybrid meshfree-Cartesian grid. Comput. Fluids 39 (3), 403–430.CrossRefGoogle Scholar
Yu, P., Yeo, K. S., Shyam Sundar, D. & Ang, S. 2011 A three-dimensional hybrid meshfree-Cartesian scheme for fluid–body interaction. Intl J. Numer. Meth. Engng 88 (4), 385–408.CrossRefGoogle Scholar
Zhang, L.2013 Unsteady aerodynamics of flapping wings. Thesis, Doctoral dissertation, National University of Singapore.Google Scholar
Zhang, Y. & Sun, M. 2010 Dynamic flight stability of a hovering model insect: lateral motion. Acta Mech. Sin. 26 (2), 175–190.CrossRefGoogle Scholar

Yao and Yeo supplementary movie 1

Movie 1 - forward flight v=1.0

Download Yao and Yeo supplementary movie 1(Video)
Video 4.2 MB

Yao and Yeo supplementary movie 2

Movie 2 - forward flight v=2.0

Download Yao and Yeo supplementary movie 2(Video)
Video 2.4 MB

Yao and Yeo supplementary movie 3

Movie 3 - sideslip manoeuvre (back view)

Download Yao and Yeo supplementary movie 3(Video)
Video 3.5 MB