Article contents
Flow structure on a rotating wing: effect of radius of gyration
Published online by Cambridge University Press: 14 August 2014
Abstract
The flow structure on a rotating wing (flat plate) is characterized over a range of Rossby number 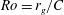 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Ro} = r_g/C$, in which
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Ro} = r_g/C$, in which 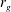 $r_g$ and
$r_g$ and 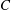 $C$ are the radius of gyration and chord of the wing, as well as travel distance
$C$ are the radius of gyration and chord of the wing, as well as travel distance  $\mathit{Ro} = r_g \Phi /C$, where
$\mathit{Ro} = r_g \Phi /C$, where 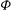 $\Phi $ is the angle of rotation. Stereoscopic particle image velocimetry (SPIV) is employed to determine the flow patterns on defined planes, and by means of reconstruction, throughout entire volumes. Images of the
$\Phi $ is the angle of rotation. Stereoscopic particle image velocimetry (SPIV) is employed to determine the flow patterns on defined planes, and by means of reconstruction, throughout entire volumes. Images of the  $Q$-criterion and spanwise vorticity, velocity and vorticity flux are employed to represent the flow structure. At low Rossby number, the leading-edge, tip and root vortices are highly coherent with large dimensionless values of
$Q$-criterion and spanwise vorticity, velocity and vorticity flux are employed to represent the flow structure. At low Rossby number, the leading-edge, tip and root vortices are highly coherent with large dimensionless values of 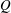 $Q$ in the interior regions of all vortices and large downwash between these components of the vortex system. For increasing Rossby number, however, the vortex system rapidly degrades, accompanied by loss of large
$Q$ in the interior regions of all vortices and large downwash between these components of the vortex system. For increasing Rossby number, however, the vortex system rapidly degrades, accompanied by loss of large 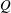 $Q$ within its interior and downstream displacement of the region of large downwash. These trends are accompanied by increased deflection of the leading-edge vorticity layer away from the surface of the wing, and decreased spanwise velocity and vorticity flux in the trailing region of the wing, which are associated with the degree of deflection of the tip vortex across the wake region. Combinations of large Rossby number
$Q$ within its interior and downstream displacement of the region of large downwash. These trends are accompanied by increased deflection of the leading-edge vorticity layer away from the surface of the wing, and decreased spanwise velocity and vorticity flux in the trailing region of the wing, which are associated with the degree of deflection of the tip vortex across the wake region. Combinations of large Rossby number 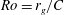 $\mathit{Ro} =r_g/C$ and travel distance
$\mathit{Ro} =r_g/C$ and travel distance 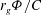 $r_g \Phi /C$ lead to separated flow patterns similar to those observed on rectilinear translating wings at high angle of attack
$r_g \Phi /C$ lead to separated flow patterns similar to those observed on rectilinear translating wings at high angle of attack  $\alpha $. In the extreme case where the wing travels a distance corresponding to a number of revolutions, the highly coherent flow structure is generally preserved if the Rossby number is small; it degrades substantially, however, at larger Rossby number.
$\alpha $. In the extreme case where the wing travels a distance corresponding to a number of revolutions, the highly coherent flow structure is generally preserved if the Rossby number is small; it degrades substantially, however, at larger Rossby number.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 48
- Cited by


