Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-25T03:47:02.242Z Has data issue: false hasContentIssue false
  • English
  • Français

Extreme motion and response statistics for survival of the three-float wave energy converter M4 in intermediate water depth

Published online by Cambridge University Press:  17 January 2017

H. Santo ,
P. H. Taylor ,
E. Carpintero Moreno ,
P. Stansby ,
R. Eatock Taylor ,
L. Sun Open the ORCID record for L. Sun [Opens in a new window]  and
J. Zang
H. Santo
Affiliation:
Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK
P. H. Taylor
Affiliation:
Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK
E. Carpintero Moreno
Affiliation:
School of Mechanical, Aerospace and Civil Engineering, University of Manchester, Manchester M13 9PL, UK
P. Stansby
Affiliation:
School of Mechanical, Aerospace and Civil Engineering, University of Manchester, Manchester M13 9PL, UK
R. Eatock Taylor
Affiliation:
Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK
L. Sun
Affiliation:
WEIR Research Unit, Department of Architecture and Civil Engineering, University of Bath, Bath BA2 7AY, UK
J. Zang
Affiliation:
WEIR Research Unit, Department of Architecture and Civil Engineering, University of Bath, Bath BA2 7AY, UK
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents both linear and nonlinear analyses of extreme responses for a multi-body wave energy converter (WEC) in severe sea states. The WEC known as M4 consists of three cylindrical floats with diameters and draft which increase from bow to stern with the larger mid and stern floats having rounded bases so that the overall system has negligible drag effects. The bow and mid float are rigidly connected by a beam and the stern float is connected by a beam to a hinge above the mid float where the rotational relative motion would be damped to absorb power in operational conditions. A range of focussed wave groups representing extreme waves were tested on a scale model without hinge damping, also representing a more general system of interconnected cylindrical floats with multi-mode forcing. Importantly, the analysis reveals a predominantly linear response structure in hinge angle and weakly nonlinear response for the beam bending moment, while effects due to drift forces, expected to be predominantly second order, are not accounted for. There are also complex and violent free-surface effects on the model during the excitation period driven by the main wave group, which generally reduce the overall motion response. Once the main group has moved away, the decaying response in the free-vibration phase decays at a rate very close to that predicted by simple linear radiation damping. Two types of nonlinear harmonic motion are demonstrated. During the free-vibration phase, there are only double and triple frequency Stokes harmonics of the linear motion, captured using a frequency doubling and tripling model. In contrast, during the excitation phase, these harmonics show much more complex behaviour associated with nonlinear fluid loading. Although bound harmonics are visible in the system response, the overall response is remarkably linear until temporary submergence of the central float (‘dunking’) occurs. This provides a strong stabilising effect for angular amplitudes greater than 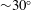${\sim}30^{\circ }$ and can be treated as a temporary loss of part of the driving wave as long as submergence continues. With an experimentally and numerically derived response amplitude operator (RAO), we perform a statistical analysis of extreme response for the hinge angle based on wave data at Orkney, well known for its severe wave climate, using the NORA10 wave hindcast. For storms with spectral peak wave periods longer than the RAO peak period, the response is controlled by the steepness of the sea state rather than the wave height. Thus, the system responds very similarly under the most extreme sea states, providing an upper bound for the most probable maximum response, which is reduced significantly in directionally spread waves. The methodology presented here is relevant to other single and multi-body systems including WECs. We also demonstrate a general and potentially important reciprocity result for linear body motion in random seas: the averaged wave history given an extreme system response and the average response history given an extreme wave match in time, with time reversed for one of the signals. This relationship will provide an efficient and robust way of defining a ‘designer wave’, for both experimental testing and computationally intensive computational fluid dynamics (CFD), for a wide range of wave–structure interaction problems.

JFM classification

Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 813 , 25 February 2017 , pp. 175 - 204
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambühl, S., Sterndorff, M. & Sørensen, J. D. 2014 Extrapolation of extreme response for different mooring line systems of floating wave energy converters. Intl J. Mar. Energy 7, 1–19.Google Scholar
Boccotti, P. 1983 Some new results on statistical properties of wind waves. Appl. Ocean Res. 5 (3), 134–140.CrossRefGoogle Scholar
Eatock Taylor, R. & Chau, F. P. 1992 Wave diffraction theory – some developments in linear and nonlinear theory. J. Offshore Mech. Arctic Engng 114 (3), 185–194.CrossRefGoogle Scholar
Eatock Taylor, R., Taylor, P. H. & Stansby, P. K. 2016 A coupled hydrodynamic-structural model of the M4 wave energy converter. J. Fluids Struct. 63, 77–96.Google Scholar
Ewans, K. C. 1998 Observations of the directional spectrum of fetch-limited waves. J. Phys. Oceanogr. 28 (3), 495–512.2.0.CO;2>CrossRefGoogle Scholar
Grice, J. R., Taylor, P. H. & Eatock Taylor, R. 2013 Near-trapping effects for multi-column structures in deterministic and random waves. J. Ocean Engng 58, 60–77.CrossRefGoogle Scholar
Grice, J. R., Taylor, P. H. & Eatock Taylor, R. 2015 Second-order statistics and designer waves for violent free-surface motion around multi-column structures. Phil. Trans. R. Soc. Lond. A 373 (2033), 20140113.Google Scholar
Jonathan, P. & Taylor, P. H. 1997 On irregular, nonlinear waves in a spread sea. J. Offshore Mech. Arctic Engng 119, 37.Google Scholar
Lindgren, G. 1970 Some properties of a normal process near a local maximum. Ann. Math. Statist. 41, 1870–1883.CrossRefGoogle Scholar
Muliawan, M. J., Gao, Z. & Moan, T. 2013a Application of the contour line method for estimating extreme responses in the mooring lines of a two-body floating wave energy converter. J. Offshore Mech. Arctic Engng 135 (3), 031301.Google Scholar
Muliawan, M. J., Karimirad, M., Gao, Z. & Moan, T. 2013b Extreme responses of a combined spar-type floating wind turbine and floating wave energy converter (STC) system with survival modes. J. Ocean Engng 65, 71–82.Google Scholar
Newland, D. E. 2006 Mechanical Vibration Analysis and Computation. Courier Corporation.Google Scholar
Newman, J. N. 1977 Marine Hydrodynamics. MIT Press.Google Scholar
Parmeggiani, S., Kofoed, J. P. & Friis-Madsen, E. 2011 Extreme loads on the mooring lines and survivability mode for the wave dragon wave energy converter. In World Renewable Energy Congress 2011.Google Scholar
Reistad, M., Breivik, Ø., Haakenstad, H., Aarnes, O. J., Furevik, B. R. & Bidlot, J. 2011 A high-resolution hindcast of wind and waves for the North Sea, the Norwegian Sea, and the Barents Sea. J. Geophys. Res. 116, C5.CrossRefGoogle Scholar
Santo, H., Taylor, P. H., Eatock Taylor, R. & Choo, Y. S. 2013 Average properties of the largest waves in Hurricane Camille. J. Offshore Mech. Arctic Engng 135, 011602.Google Scholar
Santo, H., Taylor, P. H., Eatock Taylor, R. & Stansby, P. 2016a Decadal variability of wave power production in the North-East Atlantic and North Sea for the M4 machine. J. Renew. Energy 91, 442–450.Google Scholar
Santo, H., Taylor, P. H. & Gibson, R. 2016b Decadal variability of extreme wave height representing storm severity in the northeast Atlantic and North Sea since the foundation of the Royal Society. Proc. R. Soc. Lond. A 472 (2193), 20160376.Google Scholar
Santo, H., Taylor, P. H., Woollings, T. & Poulson, S. 2015 Decadal wave power variability in the North-East Atlantic and North Sea. Geophys. Res. Lett. 42 (12), 4956–4963.Google Scholar
Socquet-Juglard, H., Dysthe, K., Trulsen, K., Krogstad, H. E. & Liu, J. 2005 Probability distributions of surface gravity waves during spectral changes. J. Fluid Mech. 542, 195–216.Google Scholar
Stallard, T. J., Weller, S. D. & Stansby, P. K. 2009 Limiting heave response of a wave energy device by draft adjustment with upper surface immersion. Appl. Ocean Res. 31 (4), 282–289.Google Scholar
Stansby, P., Carpintero Moreno, E. & Stallard, T. 2015a Capture width of the three-float multi-mode multi-resonance broadband wave energy line absorber M4 from laboratory studies with irregular waves of different spectral shape and directional spread. J. Ocean Engng Mar. Energy 1 (3), 287–298.Google Scholar
Stansby, P., Carpintero Moreno, E., Stallard, T. & Maggi, A. 2015b Three-float broad-band resonant line absorber with surge for wave energy conversion. J. Renew. Energy 78, 132–140.CrossRefGoogle Scholar
Sun, L., Eatock Taylor, R. & Taylor, P. H. 2015 Wave driven free surface motion in the gap between a tanker and an FLNG barge. Appl. Ocean Res. 51, 331–349.Google Scholar
Sun, L., Stansby, P., Zang, J., Carpintero Moreno, E. & Taylor, P. H. 2016a Linear diffraction analysis for optimisation of the three-float multi-mode wave energy converter M4 in regular waves including small arrays. J. Ocean Engng Mar. Energy 2 (4), 429–438.CrossRefGoogle Scholar
Sun, L., Zang, J., Stansby, P., Carpintero Moreno, E., Taylor, P. H. & Eatock Taylor, R. 2016b Linear diffraction analysis of the three-float multi-mode wave energy converter M4 for power capture and structural analysis in irregular waves with experimental validation. J. Ocean Engng Mar. Energy, doi:10.1007/s40722-016-0071-5.Google Scholar
Tromans, P. S., Anaturk, A. R. & Hagemeijer, P. 1991 A new model for the kinematics of large ocean waves. In Proceedings of the International Society of Offshore and Polar Engineering Conference (ISOPE-91).Google Scholar
Walker, D. A. G., Taylor, P. H. & Eatock Taylor, R. 2005 The shape of large surface waves on the open sea and the Draupner New Year wave. Appl. Ocean Res. 26 (3), 73–83.Google Scholar
Wolgamot, H. A., Taylor, P. H., Eatock Taylor, R., van den Bremer, T. S., Raby, A. C. & Whittaker, C. 2016 Experimental observation of a near-motion-trapped mode: free motion in heave with negligible radiation. J. Fluid Mech. 786, R5.Google Scholar

Santo et al. supplementary movie

Movie for the base case of Ac = 0.08 m and Tp = 1.2 sec.

Download Santo et al. supplementary movie(Video)
Video 171.4 MB

Santo et al. supplementary movie

Movie for the base case of Ac = 0.08 m and Tp = 1.2 sec.

Download Santo et al. supplementary movie(Video)
Video 21.9 MB