Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-18T06:02:01.063Z Has data issue: false hasContentIssue false
  • English
  • Français

Disorganization of a hole tone feedback loop by an axisymmetric obstacle on a downstream end plate

Published online by Cambridge University Press:  29 September 2014

K. Matsuura  and
M. Nakano
K. Matsuura*
Affiliation:
Graduate School of Science and Engineering, Ehime University, 3 Bunkyo-cho, Matsuyama, Ehime 790-8577, Japan
M. Nakano
Affiliation:
Institute of Fluid Science, Tohoku University, 2-1-1 Katahira, Aoba-ku, Sendai, Miyagi 980-8577, Japan
*
†Email address for correspondence: matsuura.kazuo.mm@ehime-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

This study investigates the suppression of the sound produced when a jet, issued from a circular nozzle or hole in a plate, goes through a similar hole in a second plate. The sound, known as a hole tone, is encountered in many practical engineering situations. The mean velocity of the air jet 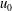$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}u_0$ was 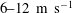$6\text {--}12\ \mathrm{m}\ {\mathrm{s}}^{-1}$. The nozzle and the end plate hole both had a diameter of 51 mm, and the impingement length $L_{im}$ between the nozzle and the end plate was 50–90 mm. We propose a novel passive control method of suppressing the tone with an axisymmetric obstacle on the end plate. We find that the effect of the obstacle is well described by the combination (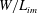$W/L_{im}$, 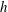$h$) where 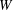$W$ is the distance from the edge of the end plate hole to the inner wall of the obstacle, and 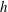$h$ is the obstacle height. The tone is suppressed when backflows from the obstacle affect the jet shear layers near the nozzle exit. We do a direct sound computation for a typical case where the tone is successfully suppressed. Axisymmetric uniformity observed in the uncontrolled case is broken almost completely in the controlled case. The destruction is maintained by the process in which three-dimensional vortices in the jet shear layers convect downstream, interact with the obstacle and recursively disturb the jet flow from the nozzle exit. While regions near the edge of the end plate hole are responsible for producing the sound in the controlled case as well as in the uncontrolled case, acoustic power in the controlled case is much lower than in the uncontrolled case because of the disorganized state.

JFM classification

Instability: Absolute/convective instability Acoustics: Aeroacoustics Wakes/Jets: Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 908 - 942
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blake, W. K. 1986 Mechanics of Flow-Induced Sound and Vibration, Vol. 1. Academic.Google Scholar
Cattafesta, L., Williams, D., Rowley, C. & Alvi, F.2003 Review of active control of flow-induced cavity resonance. AIAA Paper 2003-3567.Google Scholar
Chanaud, R. C. & Powell, A. 1965 Some experiments concerning the hole and ring tone. J. Acoust. Soc. Am. 37 (5), 902–911.Google Scholar
Freund, J. B. 1997 Proposed inflow/outflow boundary condition for direct computation of aerodynamic sound. AIAA J. 35 (4), 740–742.Google Scholar
Gad-el-Hak, M. 2000 Flow Control: Passive, Active and Reactive Flow Management. Cambridge University Press.Google Scholar
Gaitonde, D. V. & Visbal, M. R. 2000 Padé-type higher-order boundary filters for the Navier–Stokes equations. AIAA J. 38 (11), 2103–2112.Google Scholar
Ginevsky, A. S., Vlasov, Y. V. & Karavosov, R. K. 2010 Acoustic Control of Turbulent Jets. Springer.Google Scholar
Ho, C.-M. & Huerre, P. 1984 Perturbed free shear layers. Annu. Rev. Fluid Mech. 16, 365–424.Google Scholar
Howe, M. S. 1975 Contributions to the theory of aerodynamic sound, with application to excess jet noise and the theory of the flute. J. Fluid Mech. 71, 625–673.Google Scholar
Howe, M. S. 1980 The dissipation of sound at an edge. J. Sound Vib. 70 (3), 407–411.Google Scholar
Howe, M. S. 1998 Acoustics of Fluid-Structure Interactions. Cambridge University Press.Google Scholar
Izawa, S. 2011 Active and passive control of flow past a cavity. In Wind Tunnels and Experimental Fluid Dynamics Research (ed. Lerner, J. C. & Boldes, U.), pp. 369–394. InTech.Google Scholar
Langthjem, M. A. & Nakano, M. 2010 A three-dimensional study of the hole-tone feedback problem. RIMS Kôkyûroku 1697, 80–94.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.Google Scholar
Matsuura, K. & Kato, C. 2007 Large-eddy simulation of compressible transitional flows in a low-pressure turbine cascade. AIAA J. 45 (2), 442–457.Google Scholar
Matsuura, K. & Nakano, M. 2011 Direct computation of a hole-tone feedback system at very low Mach numbers. J. Fluid Sci. Technol. 6 (4), 548–561.Google Scholar
Matsuura, K. & Nakano, M. 2012 A throttling mechanism sustaining a hole tone feedback system at very low Mach numbers. J. Fluid Mech. 710, 569–605.Google Scholar
Michalke, A. 1984 Survey on jet instability theory. Prog. Aerosp. 21, 159–199.Google Scholar
Rai, M. M. & Moin, P. 1993 Direct numerical simulation of transition and turbulence in a spatially evolving boundary layer. J. Comput. Phys. 109 (2), 169–192.Google Scholar
Rayleigh, Lord 1945 Theory of Sound, Vol. 2. Dover.Google Scholar
Rockwell, D. & Naudascher, E. 1979 Self-sustained oscillations of impinging free shear layers. Annu. Rev. Fluid Mech. 11, 67–94.Google Scholar
Rossiter, J. E.1962 The effect of cavities on the buffeting of aircraft. Royal Aircraft Establishment Tech. Mem. 754.Google Scholar
Rowley, C. W. & Williams, D. R. 2006 Dynamics and control of high-Reynolds-number flow over open cavities. Annu. Rev. Fluid Mech. 38, 251–276.Google Scholar
Sirovich, L. & Rodriguez, J. D. 1987 Coherent structures and chaos: a model problem. Phys. Lett. A 120 (5), 211–214.Google Scholar
Student,   1908 The probable error of a mean. Biometrika 6 (1), 1–25.Google Scholar