Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-19T11:56:22.520Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of a counter-rotating vortex pair interacting with a wall

Published online by Cambridge University Press:  17 December 2019

Daniel Dehtyriov Open the ORCID record for Daniel Dehtyriov [Opens in a new window] ,
Kerry Hourigan Open the ORCID record for Kerry Hourigan [Opens in a new window]  and
Mark C. Thompson Open the ORCID record for Mark C. Thompson [Opens in a new window]
Daniel Dehtyriov*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria3800, Australia
Kerry Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria3800, Australia
Mark C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria3800, Australia
*
†Email address for correspondence: daniel.dehtyriov@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

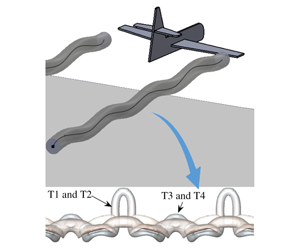
The influence of a horizontal wall on the evolution of the long-wave instability in equal strength counter-rotating vortex pairs is studied with direct numerical simulation. The two vortices descend under mutual induction and interact with a ground plane, as would aircraft trailing vortices in ground effect. Both the linear and nonlinear development of the pair is studied for three initial heights above the wall, representative of three modes of interaction identified by experiment. A study of two vortex core sizes over a range of Reynolds numbers ($1000\leqslant Re\leqslant 2500$) is used to verify parameter independence. The vortex system undergoes complex topological changes in the presence of a wall, with the separation of wall generated vorticity into hairpin-like vortex tongues and axial flow development in the primary pair. The secondary structures are rotated and stretched around the primary vortices, strongly influencing the resultant flow evolution and are comparable with those observed for oblique ring–wall interaction. Of the three modes, the small-amplitude mode shows the formation of four principal tongues per long wavelength of the Crow instability, with the secondary vortex remaining connected. The large-amplitude mode undergoes a re-connective process to form two non-planar secondary vortex structures per wavelength, and a simulation of the large ring mode in its first formation develops six tongues per wavelength. These secondary structures ‘rebound’ from the wall and interact at the symmetry plane prior to dissipation, governing the bending, stretching and trajectory of the primary vortex pair.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex instability Vortex Flows: Vortex interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A36
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asselin, D. J. & Williamson, C. H. K. 2017 Influence of a wall on the three-dimensional dynamics of a vortex pair. J. Fluid Mech. 817, 339–373.CrossRefGoogle Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bliss, D. B.1970 The dynamics of curved rotational vortex lines. Master’s thesis, Massachusetts Institute of Technology, Cambridge, MA.Google Scholar
Bourne, K., Wahono, S. & Ooi, A. 2017 Numerical investigation of vortex ring ground plane interactions. Trans. ASME J. Fluids Engng 139 (7), 071105-10.Google Scholar
Brion, V., Sipp, D. & Jacquin, L. 2007 Optimal amplification of the Crow instability. Phys. Fluids 19 (11), 111703.CrossRefGoogle Scholar
Buntine, J. D. & Pullin, D. I. 1989 Merger and cancellation of strained vortices. J. Fluid Mech. 205, 263–295.CrossRefGoogle Scholar
Cheng, M., Lou, J. & Luo, L.-S. 2010 Numerical study of a vortex ring impacting a flat wall. J. Fluid Mech. 660, 430–455.CrossRefGoogle Scholar
Couch, L. D. & Krueger, P. S. 2011 Experimental investigation of vortex rings impinging on inclined surfaces. Exp. Fluids 51 (4), 1123–1138.CrossRefGoogle Scholar
Crouch, J. 2005 Airplane trailing vortices and their control. C. R. Physique 6 (4), 487–499.CrossRefGoogle Scholar
Crouch, J. D. 1997 Instability and transient growth for two trailing-vortex pairs. J. Fluid Mech. 350, 311–330.CrossRefGoogle Scholar
Crow, S. C. 1970 Stability theory for a pair of trailing vortices. AIIA J. 8 (12), 2172–2179.CrossRefGoogle Scholar
Dee, F. W. & Nicholas, O. P.1968 Flight measurements of wing tip vortex motion near the ground. Tech. Rep. 68007. R.A.E.Google Scholar
Doering, C. R. & Gibbon, J. D. 1995 Applied Analysis of the Navier–Stokes Equations, Cambridge Texts in Applied Mathematics, vol. 1. Cambridge University Press.CrossRefGoogle Scholar
Fabre, D., Jacquin, L. & Loof, A. 2002 Optimal perturbations in a four-vortex aircraft wake in counter-rotating configuration. J. Fluid Mech. 451, 319–328.CrossRefGoogle Scholar
Fabre, D., Sipp, D. & Jacquin, L. 2006 Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551, 235–274.CrossRefGoogle Scholar
Fiedler, H. E. 1988 Coherent structures in turbulent flows. Prog. Aerosp. Sci. 25, 231–269.CrossRefGoogle Scholar
Garten, J. F., Werne, J., Fritts, D. C. & Arendt, S. 2001 Direct numerical simulations of the Crow instability and subsequent vortex reconnection in a stratified fluid. J. Fluid Mech. 426, 1–45.CrossRefGoogle Scholar
Gerz, T. & Ehret, T. 1997 Wingtip vortices and exhaust jets during the jet regime of aircraft wakes. Aerosp. Sci. Technol. 1 (7), 463–474.CrossRefGoogle Scholar
Gerz, T., Holzäpfel, F. & Darracq, D. 2002 Commercial aircraft wake vortices. Prog. Aerosp. Sci. 38 (3), 181–208.CrossRefGoogle Scholar
Haimes, R.2000 Automated fluid feature extraction from transient simulations. NASA Tech. Rep.Google Scholar
Harvey, J. K. & Perry, F. J. 1971 Flowfield produced by trailing vortices in the vicinity of the ground. AIAA 9 (8), 1659–1660.CrossRefGoogle Scholar
Hunt, J. C. R., Wray, A. & Moin, P. 1988 Eddies, stream, and convergence zones in turbulent flows. In Center for Turbulence Research Report, pp. 193–207. NASA Ames/Stanford University.Google Scholar
Hussain, A. K. M. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.CrossRefGoogle Scholar
Jacob, J. D.1995 Experimental investigation of the trailing vortex wake of rectangular airfoils. PhD thesis, University of California at Berkeley, Berkeley, CA.CrossRefGoogle Scholar
Johnson, H. G., Brion, V. & Jacquin, L. 2016 Crow instability: nonlinear response to the linear optimal perturbation. J. Fluid Mech. 795, 652–670.CrossRefGoogle Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1992 Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 238, 1–30.CrossRefGoogle Scholar
Kelvin, L. W. T. 1880 On vortex atoms. Phil. Mag. 10, 155–168.Google Scholar
Kerswell, R. R. 2002 Elliptical instability. Annu. Rev. Fluid Mech. 34 (1), 83–113.CrossRefGoogle Scholar
Klein, R., Majda, A. J. & Damodaran, K. 1995 Simplified equations for the interaction of nearly parallel vortex filaments. J. Fluid Mech. 288, 201–248.CrossRefGoogle Scholar
Kramer, W., Clercx, H. J. H. & van Heijst, G. J. F. 2007 Vorticity dynamics of a dipole colliding with a no-slip wall. Phys. Fluids 19 (12), 126603.CrossRefGoogle Scholar
Lacaze, L., Ryan, K. & Le Dizàs, S. 2007 Elliptic instability in a strained batchelor vortex. J. Fluid Mech. 577, 341–361.CrossRefGoogle Scholar
Lamb, S. H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Leweke, T. & Williamson, C. H. K. 1998 Cooperative elliptic instability of a vortex pair. J. Fluid Mech. 360, 85–119.CrossRefGoogle Scholar
Leweke, T. & Williamson, C. H. K. 2011 Experiments on long-wavelength instability and reconnection of a vortex pair. Phys. Fluids 23 (2), 024101.CrossRefGoogle Scholar
Lim, T. T. 1989 An experimental study of a vortex ring interacting with an inclined wall. Exp. Fluids 7 (7), 453–463.CrossRefGoogle Scholar
Luton, J. A. & Ragab, S. A. 1997 The three-dimensional interaction of a vortex pair with a wall. Phys. Fluids 9 (10), 2967–2980.CrossRefGoogle Scholar
Moore, D. W. & Saffman, P. G. 1971 Structure of a line vortex in an imposed strain. In Aircraft Wake Turbulence and Its Detection, pp. 339–354. Springer.CrossRefGoogle Scholar
Moore, D. W. & Saffman, P. G. 1972 The motion of a vortex filament with axial flow. Phil. Trans. R. Soc. Lond. A 272 (1226), 403–429.CrossRefGoogle Scholar
Moore, D. W. & Saffman, P. G. 1973 Axial flow in laminar trailing vortices. Proc. R. Soc. Lond. A 333 (1595), 491–508.CrossRefGoogle Scholar
Moore, D. W. & Saffman, P. G. 1975 The instability of a straight vortex filament in a strain field. Proc. R. Soc. Lond. A 346 (1646), 413–425.CrossRefGoogle Scholar
Orlandi, P. 1990 Vortex dipole rebound from a wall. Phys. Fluids A 2 (8), 1429–1436.CrossRefGoogle Scholar
Orlandi, P. & Verzicco, R. 1993 Vortex rings impinging on walls: axisymmetric and three-dimensional simulations. J. Fluid Mech. 256, 615–646.CrossRefGoogle Scholar
Peace, A. J. & Riley, N. 1983 A viscous vortex pair in ground effect. J. Fluid Mech. 129, 409–426.CrossRefGoogle Scholar
Rossow, V. J. 1999 Lift-generated vortex wakes of subsonic transport aircraft. Prog. Aerosp. Sci. 35 (6), 507–660.CrossRefGoogle Scholar
Roy, C., Leweke, T., Thompson, M. C. & Hourigan, K. 2011 Experiments on the elliptic instability in vortex pairs with axial core flow. J. Fluid Mech. 677, 383–416.CrossRefGoogle Scholar
Saffman, P. G. 1991 Approach of a vortex pair to a rigid free surface in viscous fluid. Phys. Fluids A 3 (5), 984–985.CrossRefGoogle Scholar
Scorer, R. S. & Davenport, L. J. 1970 Contrails and aircraft downwash. J. Fluid Mech. 43 (3), 451–464.CrossRefGoogle Scholar
Spalart, P. R. 1998 Airplane trailing vortices. Annu. Rev. Fluid Mech. 30 (1), 107–138.CrossRefGoogle Scholar
Stuart, T. A., Mao, X. & Gan, L. 2016 Transient growth associated with secondary vortices in ground/vortex interactions. AIAA J. 54 (6), 1901–1906.CrossRefGoogle Scholar
Swearingen, J. D., Crouch, J. D. & Handler, R. A. 1995 Dynamics and stability of a vortex ring impacting a solid boundary. J. Fluid Mech. 297, 1–28.CrossRefGoogle Scholar
Thompson, M. C., Hourigan, K., Ryan, K. & Sheard, G. J. 2006 Wake transition of two-dimensional cylinders and axisymmetric bluff bodies. J. Fluids Struct. 22 (6), 793–806; Bluff Body Wakes and Vortex-Induced Vibrations (BBVIV-4).CrossRefGoogle Scholar
Thompson, S. W. 1910 Vibrations of a columnar vortex. Math. Phys. Papers 4, 152–165.Google Scholar
Tsai, C.-Y. & Widnall, S. E. 1976 The stability of short waves on a straight vortex filament in a weak externally imposed strain field. J. Fluid Mech. 73 (4), 721–733.CrossRefGoogle Scholar
Verzicco, R. & Orlandi, P. 1994 Normal and oblique collisions of a vortex ring with a wall. Meccanica 29 (4), 383–391.CrossRefGoogle Scholar
Walker, J. D. A., Smith, C. R., Cerra, A. W. & Doligalski, T. L. 1987 The impact of a vortex ring on a wall. J. Fluid Mech. 181, 99–140.CrossRefGoogle Scholar
Widnall, S. E., Bliss, D. B. & Zalay, A. 1971 Theoretical and experimental study of the stability of a vortex pair. In Aircraft Wake Turbulence and its Detection, pp. 305–338. Springer.CrossRefGoogle Scholar

Dehtyriov et al. supplementary movie 1

An annotated animation illustrating the evolution of the small amplitude mode. See figure 12 for more details.

Download Dehtyriov et al. supplementary movie 1(Video)
Video 9.7 MB

Dehtyriov et al. supplementary movie 2

An annotated animation illustrating the evolution of the large amplitude mode. See figure 21 for more details.

Download Dehtyriov et al. supplementary movie 2(Video)
Video 9.7 MB

Dehtyriov et al. supplementary movie 3

An annotated animation illustrating the evolution of the large ring mode. See figure 28 for more details.

Download Dehtyriov et al. supplementary movie 3(Video)
Video 9.4 MB