Article contents
Deformation of leaky-dielectric fluid globules under strong electric fields: boundary layers and jets at large Reynolds numbers
Published online by Cambridge University Press: 14 October 2013
Abstract
In Taylor’s analysis of electrohydrodynamic drop deformation by a uniform electric field (Proc. R. Soc. Lond. A, vol. 291, 1966, pp. 159–166) inertia is neglected at the outset, resulting in fluid velocities that scale as the square of the applied-field magnitude. For large (i.e. millimetric) drops, with increasing field strength the Reynolds number predicted by this scaling may actually become large, suggesting the need for a complementary large-Reynolds-number investigation. Balancing viscous stresses and electrical shear forces in this limit reveals a different velocity scaling, with the 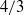 $4/ 3$-power of the applied-field magnitude. For simplicity, we focus upon the flow about a spherical gas bubble. It is essentially confined to two boundary layers propagating from the poles to the equator, where they collide to form a radial jet. The transition occurs over a small deflection region about the equator where the flow is effectively inviscid. The deviation of the bubble shape from the original sphericity is quantified by the capillary number given by the ratio of a characteristic Maxwell stress to Laplace’s pressure. At leading order the bubble deforms owing to: (i) the surface distribution of the Maxwell stress, associated with the familiar electric-field profile; (ii) the hydrodynamic boundary-layer pressure, engendered here by centrifugal forces; and (iii) the intense pressure distribution acting over the narrow equatorial deflection zone, appearing on the bubble scale as a concentrated load. Remarkably, the unique flow topology and associated scalings allow the obtaining of a closed-form expression for the deformation through the mere application of integral mass and momentum balances. On the bubble scale, the concentrated pressure load is manifested in the appearance of a non-smooth equatorial dimple.
$4/ 3$-power of the applied-field magnitude. For simplicity, we focus upon the flow about a spherical gas bubble. It is essentially confined to two boundary layers propagating from the poles to the equator, where they collide to form a radial jet. The transition occurs over a small deflection region about the equator where the flow is effectively inviscid. The deviation of the bubble shape from the original sphericity is quantified by the capillary number given by the ratio of a characteristic Maxwell stress to Laplace’s pressure. At leading order the bubble deforms owing to: (i) the surface distribution of the Maxwell stress, associated with the familiar electric-field profile; (ii) the hydrodynamic boundary-layer pressure, engendered here by centrifugal forces; and (iii) the intense pressure distribution acting over the narrow equatorial deflection zone, appearing on the bubble scale as a concentrated load. Remarkably, the unique flow topology and associated scalings allow the obtaining of a closed-form expression for the deformation through the mere application of integral mass and momentum balances. On the bubble scale, the concentrated pressure load is manifested in the appearance of a non-smooth equatorial dimple.
- Type
- Rapids
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 3
- Cited by


