Article contents
The connection between the spectrum of turbulent scales and the skin-friction statistics in channel flow at 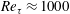 $Re_{\unicode[STIX]{x1D70F}}\approx 1000$
$Re_{\unicode[STIX]{x1D70F}}\approx 1000$
Published online by Cambridge University Press: 17 May 2019
Abstract
Data from a direct numerical simulation for channel flow at a friction Reynolds number of 1000 are analysed to derive statistical properties that offer insight into the mechanisms by which large-scale structures in the log-law region affect the small-scale turbulence field close to the wall and the statistical skin-friction properties. The data comprise full-volume velocity fields at 150 time levels separated by 50 wall-scaled viscous time units. The scales are separated into wavelength bands by means of the ‘empirical mode decomposition’, of which the two lowest modes are considered to represent the small scales and three upper modes to represent the large scales. Joint and conditional probability density functions are then derived for various scale-specific statistics, with particular emphasis placed on the streamwise and shear stresses conditional on the large-scale fluctuations of the skin friction, generally referred to as ‘footprinting’. Statistics for the small-scale stresses, conditional on the footprints, allow the amplification and attenuation of the small-scale skin friction, generally referred to as ‘modulation’, to be quantified in dependence on the footprints. The analysis leads to the conclusion that modulation does not reflect a direct interaction between small scales and large scales, but arises from variations in shear-induced production that arise from corresponding changes in the conditional velocity profile. This causal relationship also explains the wall-normal change in sign in the correlation between large scales and small scales at a wall-scaled wall distance of approximately 100. The effects of different scales on the skin friction are investigated by means of two identities that describe the relationship between the shear-stress components and the skin friction, one identity based on integral momentum and the other on energy production/dissipation. The two identities yield significant differences in the balance of scale-specific contributions, and the origins of these differences are discussed.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 28
- Cited by


