Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Camia, Federico
De Santis, Emilio
and
Newman, Charles M.
2002.
Clusters and recurrence in the two-dimensional zero-temperature stochastic ising model.
The Annals of Applied Probability,
Vol. 12,
Issue. 2,
Camia, Federico
Newman, Charles M.
and
Sidoravicius, Vladas
2002.
In and Out of Equilibrium.
p.
163.
Jain, S
2002.
Non-equilibrium dynamics of two-dimensional lattice models.
Physica A: Statistical Mechanics and its Applications,
Vol. 305,
Issue. 1-2,
p.
178.
Lima, F.W.S.
Costa Filho, R.N.
and
Costa, U.M.S.
2004.
Persistence in the zero-temperature dynamics of the random Ising ferromagnet on a Voronoi–Delaunay lattice.
Journal of Magnetism and Magnetic Materials,
Vol. 270,
Issue. 1-2,
p.
182.
Caputo, Pietro
and
Martinelli, Fabio
2006.
Phase ordering after a deep quench: the stochastic Ising and hard core gas models on a tree.
Probability Theory and Related Fields,
Vol. 136,
Issue. 1,
p.
37.
FERNANDES, F. P.
and
LIMA, F. W. S.
2008.
PERSISTENCE IN THE ZERO-TEMPERATURE DYNAMICS OF THE Q-STATES POTTS MODEL ON UNDIRECTED-DIRECTED BARABÁSI–ALBERT NETWORKS AND ERDÖS–RÉNYI RANDOM GRAPHS.
International Journal of Modern Physics C,
Vol. 19,
Issue. 12,
p.
1777.
Camia, Federico
2008.
Universality in two‐dimensional enhancement percolation.
Random Structures & Algorithms,
Vol. 33,
Issue. 3,
p.
377.
Kanoria, Yashodhan
and
Montanari, Andrea
2011.
Majority dynamics on trees and the dynamic cavity method.
The Annals of Applied Probability,
Vol. 21,
Issue. 5,
Morris, Robert
2011.
Zero-temperature Glauber dynamics on $${\mathbb{Z}^d}$$
.
Probability Theory and Related Fields,
Vol. 149,
Issue. 3-4,
p.
417.
Bušić, Ana
Fatès, Nazim
Mairesse, Jean
and
Marcovici, Irène
2012.
LATIN 2012: Theoretical Informatics.
Vol. 7256,
Issue. ,
p.
109.
Bušić, Ana
Fatès, Nazim
Mairesse, Jean
and
Marcovici, Irène
2013.
Density classification on infinite lattices and trees.
Electronic Journal of Probability,
Vol. 18,
Issue. none,
Mossel, Elchanan
Neeman, Joe
and
Tamuz, Omer
2014.
Majority dynamics and aggregation of information in social networks.
Autonomous Agents and Multi-Agent Systems,
Vol. 28,
Issue. 3,
p.
408.
Tamuz, Omer
and
Tessler, Ran J.
2015.
Majority Dynamics and the Retention of Information.
Israel Journal of Mathematics,
Vol. 206,
Issue. 1,
p.
483.
Damron, M.
Eckner, S. M.
Kogan, H.
Newman, C. M.
and
Sidoravicius, V.
2015.
Coarsening Dynamics on $$\mathbb {Z}^d$$ Z d with Frozen Vertices.
Journal of Statistical Physics,
Vol. 160,
Issue. 1,
p.
60.
Amir, Gideon
and
Baldasso, Rangel
2020.
Percolation in majority dynamics.
Electronic Journal of Probability,
Vol. 25,
Issue. none,
Damron, Michael
and
Sen, Arnab
2020.
Zero-temperature Glauber dynamics on the 3-regular tree and the median process.
Probability Theory and Related Fields,
Vol. 178,
Issue. 1-2,
p.
25.
Nguyen, Vu Xuan
Xiao, Gaoxi
Xu, Xin-Jian
Wu, Qingchu
and
Xia, Cheng-Yi
2020.
Dynamics of opinion formation under majority rules on complex social networks.
Scientific Reports,
Vol. 10,
Issue. 1,
Amir, Gideon
Baldasso, Rangel
and
Beilin, Nissan
2023.
Majority dynamics and the median process: Connections, convergence and some new conjectures.
Stochastic Processes and their Applications,
Vol. 155,
Issue. ,
p.
437.
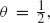 infinite spin clusters do not exist at time 0 but we show that infinite ‘spin chains’ (doubly infinite paths of vertices with a common spin) exist in abundance at any time ϵ > 0. We study the structure of the subgraph of 𝕋 generated by the vertices in time-ϵ spin chains. We show the existence of a phase transition in the sense that, for some critical θc with
infinite spin clusters do not exist at time 0 but we show that infinite ‘spin chains’ (doubly infinite paths of vertices with a common spin) exist in abundance at any time ϵ > 0. We study the structure of the subgraph of 𝕋 generated by the vertices in time-ϵ spin chains. We show the existence of a phase transition in the sense that, for some critical θc with 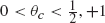 spin chains almost surely never form for θ < θc but almost surely do form in finite time for θ > θc. We relate these results to certain quantities of physical interest, such as the t → ∞ asymptotics of the probability
spin chains almost surely never form for θ < θc but almost surely do form in finite time for θ > θc. We relate these results to certain quantities of physical interest, such as the t → ∞ asymptotics of the probability 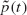 that any particular vertex changes spin after time t.
that any particular vertex changes spin after time t.

