Article contents
Weak and strong law results for a function of the spacings
Published online by Cambridge University Press: 14 July 2016
Abstract
Let 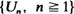 be i.i.d. uniform on (0,1) random variables and define Si,n = Ui,n–1Ui–1,n–1, i = 1, · ··, n where the Ui–n–1 are the order statistics from a sample of size n – 1 and U0,n–1 =0 and Un,n–1 = 1. The Si,n are called the spacings divided by U1,· ··,Un–1. For a fixed integer l, set
be i.i.d. uniform on (0,1) random variables and define Si,n = Ui,n–1Ui–1,n–1, i = 1, · ··, n where the Ui–n–1 are the order statistics from a sample of size n – 1 and U0,n–1 =0 and Un,n–1 = 1. The Si,n are called the spacings divided by U1,· ··,Un–1. For a fixed integer l, set 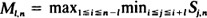 . Exact and weak limit results are obtained for the Ml,n. Further we show that with probability 1
. Exact and weak limit results are obtained for the Ml,n. Further we show that with probability 1
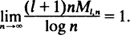 This extends results of Cheng.
This extends results of Cheng.
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1985
Footnotes
Research supported by the National Science Foundation under Grant MCS8202259 and by AFOSR Grant No. F49620 82 C 0009.
References
- 2
- Cited by


