Article contents
Transient and slim versus recurrent and fat: Random walks and the trees they grow
Published online by Cambridge University Press: 01 October 2019
Abstract
The no restart random walk (NRRW) is a random network growth model driven by a random walk that builds the graph while moving on it, adding and connecting a new leaf node to the current position of the walker every s steps. We show a fundamental dichotomy in NRRW with respect to the parity of s: for 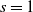 ${s}=1$
we prove that the random walk is transient and non-leaf nodes have degrees bounded above by an exponential distribution; for s even we prove that the random walk is recurrent and non-leaf nodes have degrees bounded below by a power law distribution. These theoretical findings highlight and confirm the diverse and rich behaviour of NRRW observed empirically.
${s}=1$
we prove that the random walk is transient and non-leaf nodes have degrees bounded above by an exponential distribution; for s even we prove that the random walk is recurrent and non-leaf nodes have degrees bounded below by a power law distribution. These theoretical findings highlight and confirm the diverse and rich behaviour of NRRW observed empirically.
MSC classification
- Type
- Research Papers
- Information
- Copyright
- © Applied Probability Trust 2019
References
- 2
- Cited by


