Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-29T17:20:42.838Z Has data issue: false hasContentIssue false
  • English
  • Français

Super-extremal processes and the argmax process

Part of: Stochastic processes

Published online by Cambridge University Press:  14 July 2016

Sidney I. Resnick  and
Rishin Roy
Sidney I. Resnick*
Affiliation:
Cornell University
Rishin Roy*
Affiliation:
University of Toronto
*
∗Postal address: School of Operations Research and Industrial Engineering, ETC Building, Cornell University, Ithaca, NY 14853, USA.
∗∗Present address: Paribas Corporation, Equitable Tower, 787 7th Avenue, New York, NY 10019, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we develop the probabilistic foundations of the dynamic continuous choice problem. The underlying choice set is a compact metric space E such as the unit interval or the unit square. At each time point t, utilities for alternatives are given by a random function 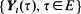. To achieve a model of dynamic continuous choice, the theory of classical vector-valued extremal processes is extended to super-extremal processesY= {Yt, t > 0}. At any t > 0, Yt is a random upper semicontinuous function on a locally compact, separable, metric space E. General path properties of Y are discussed and it is shown that Y is Markov with state-space US(E). For each t > 0, Yt is associated.

For a compact metric E, we consider the argmax process M = {Mt, t > 0}, where 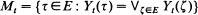. In the dynamic continuous choice application, the argmax process M represents the evolution of the set of random utility maximizing alternatives. M is a closed set-valued random process, and its path properties are investigated.

Keywords

DYNAMIC CONTINUOUS CHOICERANDOM CLOSED SETRANDOM UPPER SEMICONTINUOUS FUNCTIONSUPER-EXTREMAL PROCESSPOISSON PROCESSCLOSED SET-VALUED PROCESS

MSC classification

Primary: 60G70: Extreme value theory; extremal processes
Secondary: 60G55: Point processes
Type
Research Article
Information
Journal of Applied Probability , Volume 31 , Issue 4 , December 1994 , pp. 958 - 978
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Partially supported by NSF Grant DMS 9100027.

Partially supported by the Natural Sciences and Engineering Research Council of Canada.

References

Balkema, A. A., Haan, L. De and Karandikar, R. L. (1993) The maximum of n independent processes. J. Appl. Prob. 30, 66–81.CrossRefGoogle Scholar
Beer, G. (1982) Upper semicontinuous functions and the Stone approximation theorem. J. Approx. Theory 34, 1–11.CrossRefGoogle Scholar
Beer, G. and Kenderov, P. (1988) On the argmin multifunction for lower semicontinuous functions. Proc. Amer. Math. Soc. 102, 107–113.CrossRefGoogle Scholar
Burton, R. and Waymire, E. (1985) Scaling limits and associated random measures. Ann. Prob. 13, 1267–1278.CrossRefGoogle Scholar
Castaing, C. and Valadier, M. (1977) Convex Analysis and Measurable Multifunctions. Lecture Notes in Mathematics 580, Springer-Verlag, New York.CrossRefGoogle Scholar
Chintagunta, P. and Roy, R. (1993) A framework for investigating habits, hand-of-the-past and heterogeneity in dynamic brand choice. Working paper, University of Toronto.Google Scholar
Cosslett, S. (1988) Extreme-value stochastic processes: A model of random utility maximization for a continuous choice set. Working paper, Ohio State University.Google Scholar
Dagsvik, J. (1983) Discrete dynamic choice: an extension of the choice models of Luce and Thurstone. J. Math. Psychol. 27, 1–43.CrossRefGoogle Scholar
Dagsvik, J. (1990) Discrete and continuous choice, max-stable processes, and independence of irrelevant alternatives. Working paper, Central Bureau of Statistics, Oslo, Norway.Google Scholar
Dellacherie, C. and Meyer, P.-A. (1978) Probabilities and Potential , Vol. I. North-Holland, New York.Google Scholar
Dolecki, S., Salinetti, G. and Wets, R. J.-B. (1983) Convergence of functions: equisemicontinuity. Trans. Amer. Math. Soc. 276, 409–429.CrossRefGoogle Scholar
Dudley, R. M. Real Analysis and Probability. Wadsworth and Brooks/Cole, Belmont, CA.CrossRefGoogle Scholar
Esary, J., Proschan, F. and Walkup, D. (1967) Association of random variables, with applications. Ann. Math. Statist. 38, 1466–1474.CrossRefGoogle Scholar
Gine, E., Hahn, M. and Vatan, P. (1990) Max-infinite divisibility and max-stable sample continuous processes. Prob. Theory Rel. Fields 87, 139–165.CrossRefGoogle Scholar
Lindqvist, B. H. (1988) Association of probability measures on partially-ordered spaces. J. Multivariate Anal. 26, 111–132.CrossRefGoogle Scholar
Mcfadden, D. (1981) Econometric models of probabilistic choice. In Structural Analysis of Discrete Choice Data , ed. Manski, C. and McFadden, D., pp. 198–272, MIT Press, Cambridge, MA.Google Scholar
Norberg, T. (1986) Random capacities and their distributions. Prob. Theory Rel. Fields 73, 281–297.CrossRefGoogle Scholar
Resnick, S. I. (1987) Extreme Values, Regular Variation, and Point Processes. Springer-Verlag, New York.CrossRefGoogle Scholar
Resnick, S. I. and Roy, R. (1990) Multivariate extremal processes, leader processes and dynamic choice models. Adv. Appl. Prob. 22, 309–331.CrossRefGoogle Scholar
Resnick, S. I. and Roy, R. (1991) Random usc functions, max-stable processes and continuous choice. Ann. Appl. Prob. 1, 267–292.CrossRefGoogle Scholar
Resnick, S. I. and Roy, R. (1994) Super-extremal processes, max-stability and dynamic continuous choice. Ann. Appl. Prob. 4(3).CrossRefGoogle Scholar
Roy, R. (1991) A general framework for modeling consumer choice dynamics. Working paper, University of Toronto.Google Scholar
Vervaat, W. (1988) Random upper semicontinuous functions and extremal processes. In Probability and Lattices. CWI Tracts, forthcoming.Google Scholar
Whitt, W. (1980) Some useful functions for functional limit theorems. Math. Operat Res. 5, 67–85.CrossRefGoogle Scholar