Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-17T16:45:57.671Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic vector difference equations with stationary coefficients

Part of: Stochastic processes Stochastic analysis

Published online by Cambridge University Press:  14 July 2016

Paul Glasserman  and
David D. Yao
Paul Glasserman*
Affiliation:
Columbia University
David D. Yao*
Affiliation:
Columbia University
*
∗Postal address: Graduate School of Business, and
∗∗IE/OR Department, Columbia University, New York, NY10027, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

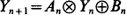We give a unified presentation of stability results for stochastic vector difference equations based on various choices of binary operations 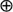and 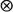, assuming that 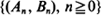are stationary and ergodic. In the scalar case, under standard addition and multiplication, the key condition for stability is E[log |A0|] < 0. In the generalizations, the condition takes the form γ< 0, where γis the limit of a subadditive process associated with 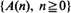. Under this and mild additional conditions, the process 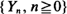has a unique finite stationary distribution to which it converges from all initial conditions.

The variants of standard matrix algebra we consider replace the operations + and × with (max, +), (max,×), (min, +), or (min,×). In each case, the appropriate stability condition parallels that for the standard recursions, involving certain subadditive limits. Since these limits are difficult to evaluate, we provide bounds, thus giving alternative, computable conditions for stability.

Keywords

RANDOM MATRICESSTABILITYSUBADDITIVE ERGODIC THEORY

MSC classification

Primary: 60H25: Random operators and equations
Secondary: 60G10: Stationary processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 32 , Issue 4 , December 1995 , pp. 851 - 866
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Baccelli, F. and Konstantopoulos, T. (1991) Estimates of cycle times in stochastic Petri nets. In Applied Stochastic Analysis. Lecture Notes in Control and Information Sciences 177, pp. 1–20. Springer, New York.Google Scholar
[2] Baccelli, F. and Liu, Z. (1992) On a class of stochastic recursive sequences arising in queueing theory. Ann. Prob. 20, 350–374.CrossRefGoogle Scholar
[3] Baccelli, F., Cohen, G., Olsder, G. J. and Quadrat, J.-P. (1992) Synchronization and Linearity. Wiley, Chichester.Google Scholar
[4] Bougerol, P. and Picard, N. (1992) Strict stationarity of generalized autoregressive sequences. Ann. Prob. 20, 1714–1730.CrossRefGoogle Scholar
[5] Brandt, A. (1986) The stochastic equation Yn+1 = An Yn + Bn with stationary coefficients. Adv. Appl. Prob. 18, 211–220.Google Scholar
[6] Brandt, A., Franken, P. and Lisek, B. (1990) Stationary Stochastic Models. Wiley, New York.Google Scholar
[7] Cohen, J. E. (1988) Subadditivity, generalized products of random matrices and operations research. SIAM Review 30, 69–86.CrossRefGoogle Scholar
[8] Cohen, J. E., Kesten, H. and Newman, C. M., (eds) (1986) Random Matrices and Their Applications. Contemporary Mathematics 50, American Mathematical Society, Providence, RI.Google Scholar
[9] Cunninghame-Green, R. (1979) Minimax Algebra. Lecture Notes in Economics and Mathematical Systems 166, Springer-Verlag, New York.Google Scholar
[10] Daley, D. J. and Haslett, J. (1982) A thermal energy storage process with controlled input. Adv. Appl. Prob. 14, 257–271.CrossRefGoogle Scholar
[11] Furstenberg, H. and Kesten, H. (1960) Products of random matrices. Ann. Math. Statist. 31, 457–469.Google Scholar
[12] Glasserman, P. (1993) Stationary waiting time derivatives. QUESTA 12, 369–390.Google Scholar
[13] Heyde, C. C. and Cohen, J. E. (1985) Confidence intervals for demographic projections based on products of random matrices. Theor. Popn Biol. 27, 120–153.CrossRefGoogle ScholarPubMed
[14] Kesten, H. (1973) Random difference equations and renewal theory for products of random matrices. Acta Math. 131, 207–248.CrossRefGoogle Scholar
[15] Kingman, J. F. C. (1973) Subadditive ergodic theory. Ann. Prob. 1, 883–909.CrossRefGoogle Scholar
[16] Kingman, J. F. C. (1975) The first birth problem for an age-dependent branching process. Ann. Prob. 3, 790–801.Google Scholar
[17] Loynes, R. M. (1962) The stability of a queue with non-independent inter-arrival and service times. Proc. Camb. Phil. Soc. 58, 497–520.CrossRefGoogle Scholar
[18] Seneta, E. (1973) Non-Negative Matrices. Wiley, New York.Google Scholar
[19] Vervaat, W. (1979) On a stochastic difference equation and a representation of non-negative infinitely divisible random variables. Adv. Appl. Prob. 11, 750–783.Google Scholar
[20] Whitt, W. (1990) Queues with service times and interarrival times depending linearly and randomly upon waiting times. QUESTA 6, 335–352.Google Scholar