Hostname: page-component-77c89778f8-gvh9x Total loading time: 0 Render date: 2024-07-17T04:06:20.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Saddlepoint approximations in conditional inference

Published online by Cambridge University Press:  14 July 2016

Suojin Wang
Suojin Wang*
Affiliation:
Texas A&M University
*
∗∗ Postal address: Department of Statistics, Texas A&M University, College Station, TX 77843, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

Saddlepoint approximations are derived for the conditional cumulative distribution function and density of 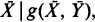where 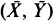is the sample mean of n i.i.d. bivariate random variables and g(x, y) is a non-linear function. The relative error of order O(n–1) is retained. The results extend the important work of Skovgaard (1987), and are useful in conditional inference, especially in the case of small or moderate sample sizes. Generalizations to higher-dimensional random vectors are also discussed. Some examples are demonstrated.

Keywords

ASYMPTOTIC EXPANSIONCONDITIONAL DENSITYCONDITIONAL DISTRIBUTIONCONDITIONAL INFERENCENON-LINEAR CONDITIONING
Type
Research Papers
Information
Journal of Applied Probability , Volume 30 , Issue 2 , June 1993 , pp. 397 - 404
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bleistein, N. (1966) Uniform asymptotic expansions of integrals with stationary points near algebraic singularity. Comm. Pure. Appl. Math. 19, 357–370.Google Scholar
Cox, D. R. and Hinkley, D. V. (1974) Theoretical Statistics. Chapman and Hall, London.Google Scholar
Daniels, H. E. (1987) Tail probability approximations. Internat. Statist. Rev. 55, 37–48.CrossRefGoogle Scholar
Davison, A. C. (1988) Approximate conditional inference in generalized linear models. J. R. Statist. Soc. B 50, 445–461.Google Scholar
Davison, A. C. and Hinkley, D. V. (1988) Saddlepoint approximations in resampling methods. Biometrika 75, 417–431.Google Scholar
Hinkley, D. V. (1977) Conditional inference about a normal mean with known coefficient of variation. Biometrika 64, 105–108.CrossRefGoogle Scholar
Jeffreys, H. and Jeffreys, B.S. (1962) Methods of Mathematical Physics, 3rd edn. Cambridge University Press.Google Scholar
Lugannani, R. and Rice, S. O. (1980) Saddlepoint approximation for the distribution of the sum of independent random variables. Adv. Appl. Prob. 12, 475–490.Google Scholar
Reid, N. (1988) Saddlepoint methods and statistical inference (with discussion). Statist. Sci. 3, 213–238.Google Scholar
Skovgaard, I. M. (1987) Saddlepoint expansions for conditional distributions. J. Appl. Prob. 24, 875–887.Google Scholar
Temme, N. M. (1982) The uniform asymptotic expansion of a class of integrals related to cumulative distribution functions. SIAM J. Math. Anal. 13, 239–251.Google Scholar
Tierney, L., Kass, R. E. and Kadane, J. B. (1989) Approximate marginal densities of nonlinear functions. Biometrika 76, 425–433.Google Scholar
Wang, S. (1990) Saddlepoint approximations in resampling analysis. Ann. Inst. Statist. Math. 42, 115–131.Google Scholar