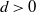1. Introduction
Consider the surplus process X of an insurance portfolio. We will use the notation
![]() $\overline{X}$
for the running maximum and D for the (absolute) drawdown process of X,
$\overline{X}$
for the running maximum and D for the (absolute) drawdown process of X,
![]() $D_t = \overline{X}\mspace{-1mu}_t - X_t$
. We allow for some ‘initial drawdown’
$D_t = \overline{X}\mspace{-1mu}_t - X_t$
. We allow for some ‘initial drawdown’
![]() $D_{0}=\overline{X}\mspace{-1mu}_0 - X_0>0$
at the beginning of the observation period. We denote the first time where the drawdown is larger than a level
$D_{0}=\overline{X}\mspace{-1mu}_0 - X_0>0$
at the beginning of the observation period. We denote the first time where the drawdown is larger than a level
![]() $y\geq 0$
by
$y\geq 0$
by
![]() $\vartheta^y = \inf\{t \ge 0\,{:}\, D_t > y\}$
. In this paper we examine how (proportional) reinsurance as stochastic control can be used to minimise the time the drawdown exceeds some critical level
$\vartheta^y = \inf\{t \ge 0\,{:}\, D_t > y\}$
. In this paper we examine how (proportional) reinsurance as stochastic control can be used to minimise the time the drawdown exceeds some critical level
![]() $d>0$
.
$d>0$
.
There are many reasons why companies and, in particular, insurers might want to reduce the probability and size of drawdowns. A crucial example is reputational risk. An insurer with stable surpluses will be more trustworthy and is therefore likely be more effective in the acquisition of new customers. Conversely, a large drawdown, even if it is not large enough to affect the company’s overall capital, can unsettle (potential) customers who read bad news in newspapers. Another interpretation could be dividend payments according to a barrier strategy. While the surplus in a Markovian risk model tends to infinity, it will be bounded in practice. A larger surplus will be paid as a dividend. The reflection of the process D at zero may therefore be seen as a reflection at a dividend barrier. The barrier d is then interpreted as a solvency level and the time in the critical drawdown area is the time in the red.
Drawdowns have received particular attention recently in financial mathematics; see, for example, [Reference Landriault, Li and Zhang14, Reference Mijatović and Pistorius15, Reference Zhang20, Reference Zhang, Leung and Hadjiliadis21]. The main topic is the distribution of
![]() $\vartheta^d$
and some related quantities. In a series of papers, the optimal investment problem in a Black–Scholes market was considered where either the probability of a drawdown or the time in drawdown for an exponential lifetime has to be minimised [Reference Angoshtari, Bayraktar and Young2, Reference Angoshtari, Bayraktar and Young3, Reference Angoshtari, Bayraktar and Young4, Reference Chen, Landriault, Li and Li7]. A variant is considering the proportional drawdown
$\vartheta^d$
and some related quantities. In a series of papers, the optimal investment problem in a Black–Scholes market was considered where either the probability of a drawdown or the time in drawdown for an exponential lifetime has to be minimised [Reference Angoshtari, Bayraktar and Young2, Reference Angoshtari, Bayraktar and Young3, Reference Angoshtari, Bayraktar and Young4, Reference Chen, Landriault, Li and Li7]. A variant is considering the proportional drawdown
![]() $\{D_t > \alpha \overline{X}\mspace{-1mu}_t\}$
for some
$\{D_t > \alpha \overline{X}\mspace{-1mu}_t\}$
for some
![]() $\alpha \in(0,1)$
. In an actuarial context a diffusion approximation is often used to model the surplus of an insurance portfolio. We assume that X is already discounted. That means we measure all monetary units referenced to time zero. Otherwise, the premium rate and the claim sizes should increase with inflation. Thus, a riskless rate of interest is not present. A possible quantity to consider could be the ruin probability under proportional drawdown
$\alpha \in(0,1)$
. In an actuarial context a diffusion approximation is often used to model the surplus of an insurance portfolio. We assume that X is already discounted. That means we measure all monetary units referenced to time zero. Otherwise, the premium rate and the claim sizes should increase with inflation. Thus, a riskless rate of interest is not present. A possible quantity to consider could be the ruin probability under proportional drawdown
![]() ${\mathbb{P}}\big[D_t > \alpha \overline{X}\mspace{-1mu}_t\big]$
. This can be seen as the risk model with tax considered in [Reference Albrecher and Hipp1]. Since the ruin level
${\mathbb{P}}\big[D_t > \alpha \overline{X}\mspace{-1mu}_t\big]$
. This can be seen as the risk model with tax considered in [Reference Albrecher and Hipp1]. Since the ruin level
![]() $\alpha \overline{X}\mspace{-1mu}_t$
increases whenever the process is at a maximum, we could consider the surplus process
$\alpha \overline{X}\mspace{-1mu}_t$
increases whenever the process is at a maximum, we could consider the surplus process
![]() $X_t - (1-\alpha)\overline{X}\mspace{-1mu}_t$
which corresponds to the model with tax rate
$X_t - (1-\alpha)\overline{X}\mspace{-1mu}_t$
which corresponds to the model with tax rate
![]() $(1-\alpha)$
. Moreover, it cannot be optimal to keep an arbitrarily large surplus because either the regulator would intervene or the shareholders would demand a dividend. We therefore keep the critical drawdown constant.
$(1-\alpha)$
. Moreover, it cannot be optimal to keep an arbitrarily large surplus because either the regulator would intervene or the shareholders would demand a dividend. We therefore keep the critical drawdown constant.
An exponentially distributed lifetime is not appropriate in this case either. Insurance contracts induce a deterministic time horizon and business decisions should use an infinite horizon. We will consider here an infinite horizon and want to minimise the time spent in drawdown. For our problem, stopping at ruin would not be a good idea: it may be optimal to get ruined as quickly as possible in order not be punished by future drawdowns. Because the process might then spend an infinite time in drawdown, we discount the quantity of interest. This is a preference measure and can be seen as preferring drawdowns tomorrow to a drawdown today.
In this paper we work with the diffusion approximation
see, for example, [Reference Grandell9, Reference Schmidli18]. Here,
![]() $\eta$
is the safety loading and
$\eta$
is the safety loading and
![]() $\sigma>0$
represents the volatility of claim payments. The stochastic quantities are defined on a complete probability space
$\sigma>0$
represents the volatility of claim payments. The stochastic quantities are defined on a complete probability space
![]() $(\Omega, \mathcal{{F}}, {\mathbb{P}})$
. We use the natural filtration
$(\Omega, \mathcal{{F}}, {\mathbb{P}})$
. We use the natural filtration
![]() $\{\mathcal{{F}}_t\}$
generated by the Brownian motion W. That is, the smallest right continuous filtration such that W is adapted. To the surplus process we append the value
$\{\mathcal{{F}}_t\}$
generated by the Brownian motion W. That is, the smallest right continuous filtration such that W is adapted. To the surplus process we append the value
![]() $u(x) = {\mathbb{E}}^{x}\big[ \int_0^\infty \textrm{e}^{-\delta t} \textbf{1}_{\{ D_t > d \} } \,\textrm{d}t\big]$
, where
$u(x) = {\mathbb{E}}^{x}\big[ \int_0^\infty \textrm{e}^{-\delta t} \textbf{1}_{\{ D_t > d \} } \,\textrm{d}t\big]$
, where
![]() $\delta > 0$
is the preference parameter.
$\delta > 0$
is the preference parameter.
![]() ${\mathbb{E}}^x$
denotes the conditional expectation with respect to
${\mathbb{E}}^x$
denotes the conditional expectation with respect to
![]() $\{D_0 = x\}$
. It should be noted that the expected time u(x) spent ‘critically’ far from the running maximum does not depend on the initial surplus but only on the initial drawdown. This is due to the fact that the initial drawdown is invariant to distance-preserving shifts of the initial surplus and initial maximum. Another important observation is, that, as a linear transformation of the Markovian pair
$\{D_0 = x\}$
. It should be noted that the expected time u(x) spent ‘critically’ far from the running maximum does not depend on the initial surplus but only on the initial drawdown. This is due to the fact that the initial drawdown is invariant to distance-preserving shifts of the initial surplus and initial maximum. Another important observation is, that, as a linear transformation of the Markovian pair
![]() $(X,\overline{X})$
, the drawdown process D ‘inherits’ the Markov property (compare, for example, [Reference Pilipenko16, Chapter 1]).
$(X,\overline{X})$
, the drawdown process D ‘inherits’ the Markov property (compare, for example, [Reference Pilipenko16, Chapter 1]).
The cedent may buy proportional reinsurance. The reinsurance premium is calculated at safety loading
![]() $\theta$
. In order for the problem not to be trivial, we let
$\theta$
. In order for the problem not to be trivial, we let
![]() $\theta >\eta$
. In this model the insurer may decide on his retention level
$\theta >\eta$
. In this model the insurer may decide on his retention level
![]() $b_{t}$
at every point in time t such that the reinsurance strategy
$b_{t}$
at every point in time t such that the reinsurance strategy
![]() $b = \{b_t\}$
is an adapted càdlàg process with
$b = \{b_t\}$
is an adapted càdlàg process with
![]() $b_t \in [0,1]$
. The surplus
$b_t \in [0,1]$
. The surplus
![]() $X^{b}$
under the strategy b takes the form
$X^{b}$
under the strategy b takes the form
![]() $X_{t}^{b} = X_{0} + \int_{0}^{t} [\eta- (1-b_{s})\theta] \,\textrm{d} s + \int_{0}^{t}b_{s}\sigma \,\textrm{d} W_{s}$
(
$X_{t}^{b} = X_{0} + \int_{0}^{t} [\eta- (1-b_{s})\theta] \,\textrm{d} s + \int_{0}^{t}b_{s}\sigma \,\textrm{d} W_{s}$
(
![]() $t \geq 0$
; see also, for example, [Reference Schmidli18]), and
$t \geq 0$
; see also, for example, [Reference Schmidli18]), and
![]() $\overline{X^{b}}$
and
$\overline{X^{b}}$
and
![]() $D^{b}$
are defined accordingly:
$D^{b}$
are defined accordingly:
![]() $D_{t}^{b} =\max_{s\leq t} X_{s}^{b} - X_{t}^{b}=\overline{X_{t}^{b}}-X_{t}^{b}$
(
$D_{t}^{b} =\max_{s\leq t} X_{s}^{b} - X_{t}^{b}=\overline{X_{t}^{b}}-X_{t}^{b}$
(
![]() $t \geq 0$
). Following the strategy b, the value is
$t \geq 0$
). Following the strategy b, the value is
![]() $v^b(x) ={\mathbb{E}}^{x}\big[ \int_0^\infty \textrm{e}^{-\delta t} \textbf{1}_{\{ D^b_t > d \} } \,\textrm{d} t\big]$
, which, for the constant retention level strategy
$v^b(x) ={\mathbb{E}}^{x}\big[ \int_0^\infty \textrm{e}^{-\delta t} \textbf{1}_{\{ D^b_t > d \} } \,\textrm{d} t\big]$
, which, for the constant retention level strategy
![]() $b_t\equiv 1$
, coincides with u(x). We are interested in an optimal strategy b which minimises the value. Hence,
$b_t\equiv 1$
, coincides with u(x). We are interested in an optimal strategy b which minimises the value. Hence,
![]() $v(x) = \inf_b v^b(x)$
is the value function where we minimise over all adapted càdlàg strategies. Similarly to the function u(x),
$v(x) = \inf_b v^b(x)$
is the value function where we minimise over all adapted càdlàg strategies. Similarly to the function u(x),
![]() $v^b(x)$
does not depend on the initial, absolute positions of the surplus process and the maximum, but only on their distance. As it turns out, the optimal retention level strategy is of ‘feedback form’. That is to say, the optimal retention level at time t is given by
$v^b(x)$
does not depend on the initial, absolute positions of the surplus process and the maximum, but only on their distance. As it turns out, the optimal retention level strategy is of ‘feedback form’. That is to say, the optimal retention level at time t is given by
![]() $ b^\ast(D_t^b)$
for a measurable function
$ b^\ast(D_t^b)$
for a measurable function
![]() $b^\ast \,{:}\, [0, \infty) \to [0,1]$
. In particular, a feedback strategy does not depend on the history of the drawdown process and therefore preserves the Markov property.
$b^\ast \,{:}\, [0, \infty) \to [0,1]$
. In particular, a feedback strategy does not depend on the history of the drawdown process and therefore preserves the Markov property.
Our first step towards solving this optimisation problem is the observation that the value function obeys a dynamic programming principle. For any admissibly controlled drawdown process we can condition on the first time of reaching the level d. Let
![]() $\vartheta^{y}(b)\,{:\!=}\, \inf \big\{t\geq 0 \,{:}\, D_{t}^{b} > y \big\}$
if
$\vartheta^{y}(b)\,{:\!=}\, \inf \big\{t\geq 0 \,{:}\, D_{t}^{b} > y \big\}$
if
![]() $y > x$
and
$y > x$
and
![]() $\vartheta_{y}(b)\,{:\!=}\, \inf\{ t\geq 0 \,{:}\, D_{t}^{b} < y \}$
if
$\vartheta_{y}(b)\,{:\!=}\, \inf\{ t\geq 0 \,{:}\, D_{t}^{b} < y \}$
if
![]() $y < x$
be the time of the first passage through y of the drawdown process under the strategy b, and
$y < x$
be the time of the first passage through y of the drawdown process under the strategy b, and
![]() $\vartheta (b)\,{:\!=}\, \vartheta_{d}(b) \vee \vartheta^d(b)$
. We define the stopping time
$\vartheta (b)\,{:\!=}\, \vartheta_{d}(b) \vee \vartheta^d(b)$
. We define the stopping time
![]() $\vartheta(b)$
as the first passage time through d, in order that we do not need to distinguish between starting in
$\vartheta(b)$
as the first passage time through d, in order that we do not need to distinguish between starting in
![]() $x > d$
or
$x > d$
or
![]() $x < d$
. Then, if we denote by
$x < d$
. Then, if we denote by
![]() $\tilde b_t = b_{\vartheta(b) + t}$
the strategy after the first passage through d, we have
$\tilde b_t = b_{\vartheta(b) + t}$
the strategy after the first passage through d, we have
![]() $v^{b}(x) = {\mathbb{E}}^{x}\big[\textrm{e}^{-\delta \vartheta (b)}v^{\tilde{b}}(d) \big] \geq v(d) {\mathbb{E}}^{x}\big[\textrm{e}^{-\delta \vartheta (b)}\big]$
for
$v^{b}(x) = {\mathbb{E}}^{x}\big[\textrm{e}^{-\delta \vartheta (b)}v^{\tilde{b}}(d) \big] \geq v(d) {\mathbb{E}}^{x}\big[\textrm{e}^{-\delta \vartheta (b)}\big]$
for
![]() $x \leq d$
. Hence, taking the infimum over all possible compositions of strategies, we get
$x \leq d$
. Hence, taking the infimum over all possible compositions of strategies, we get
![]() $v(x)\geq v(d) \inf_{b} {\mathbb{E}}^{x}\big[\textrm{e}^{-\delta \vartheta (b)}\big] $
. Conversely, we get
$v(x)\geq v(d) \inf_{b} {\mathbb{E}}^{x}\big[\textrm{e}^{-\delta \vartheta (b)}\big] $
. Conversely, we get
![]() $v(x) \leq {\mathbb{E}}^{x}\big[\textrm{e}^{-\delta \vartheta (b)}\big]v^{\tilde{b}}(d) $
for any strategy such that
$v(x) \leq {\mathbb{E}}^{x}\big[\textrm{e}^{-\delta \vartheta (b)}\big]v^{\tilde{b}}(d) $
for any strategy such that
![]() $\tilde b$
does not depend on the history of the process up to the first passage through d. Taking the infimum, firstly for
$\tilde b$
does not depend on the history of the process up to the first passage through d. Taking the infimum, firstly for
![]() $\tilde{b}$
and then for b, yields
$\tilde{b}$
and then for b, yields
![]() $v(x)= v(d) \inf_{b} {\mathbb{E}}^{x}\big[\textrm{e}^{-\delta \vartheta (b)}\big] $
. Similarly, if
$v(x)= v(d) \inf_{b} {\mathbb{E}}^{x}\big[\textrm{e}^{-\delta \vartheta (b)}\big] $
. Similarly, if
![]() $x>d$
,
$x>d$
,
![]() $v(x) = \delta^{-1} \big\{1-(1-\delta v(d)) \sup_{b} {\mathbb{E}}^{x}\big[\textrm{e}^{-\delta\vartheta (b)}\big] \big\}$
. This observation is summarised in the following lemma.
$v(x) = \delta^{-1} \big\{1-(1-\delta v(d)) \sup_{b} {\mathbb{E}}^{x}\big[\textrm{e}^{-\delta\vartheta (b)}\big] \big\}$
. This observation is summarised in the following lemma.
Lemma 1.1. The value function fulfils
 \begin{equation*} v(x) = \begin{cases}v(d) \inf_{b} {\mathbb{E}}^{x}[\textrm{e}^{-\delta \vartheta (b)}] , & \text{if $x < d$,}\\ \\[-7pt] \delta^{-1} \{1-(1-\delta v(d)) \sup_{b} {\mathbb{E}}^{x}[\textrm{e}^{-\delta\vartheta (b)}] \} , & \text{if $x > d$.}\end{cases}\end{equation*}
\begin{equation*} v(x) = \begin{cases}v(d) \inf_{b} {\mathbb{E}}^{x}[\textrm{e}^{-\delta \vartheta (b)}] , & \text{if $x < d$,}\\ \\[-7pt] \delta^{-1} \{1-(1-\delta v(d)) \sup_{b} {\mathbb{E}}^{x}[\textrm{e}^{-\delta\vartheta (b)}] \} , & \text{if $x > d$.}\end{cases}\end{equation*}
In particular, the strategy to minimise
![]() ${\mathbb{E}}^{x}[\textrm{e}^{-\delta \vartheta (b)}]$
is also optimal for our problem in [0, d), and the strategy to maximise
${\mathbb{E}}^{x}[\textrm{e}^{-\delta \vartheta (b)}]$
is also optimal for our problem in [0, d), and the strategy to maximise
![]() ${\mathbb{E}}^{x}\big[\textrm{e}^{-\delta\vartheta (b)}\big]$
is optimal in
${\mathbb{E}}^{x}\big[\textrm{e}^{-\delta\vartheta (b)}\big]$
is optimal in
![]() $(d,\infty)$
.
$(d,\infty)$
.
This means we can split the problem into two separate problems which have the interpretation of maximising the time in the uncritical area [0, d) and minimising the time within
![]() $(d,\infty)$
.
$(d,\infty)$
.
We start by considering the value function without optimisation in Section 2. In Section 3 we solve the easier subproblem of large initial drawdown and discover that the optimal strategy is the constant ‘maximum drift’ strategy of
![]() $b_t=1$
,
$b_t=1$
,
![]() $t\geq 0$
. Section 4 deals with the case where the initial drawdown is smaller than d. Here we analyse the optimiser of the Hamilton–Jacobi–Bellman equation to find a solution fitting the preconditions. We distinguish between ‘cheap’ and ‘expensive’ reinsurance which lead to different types of optimal strategies. We obtain explicit expressions for the optimiser and conclude that the optimal strategy is an increasing function of the current drawdown. In particular, the retention level optimally chosen for a zero drawdown is
$t\geq 0$
. Section 4 deals with the case where the initial drawdown is smaller than d. Here we analyse the optimiser of the Hamilton–Jacobi–Bellman equation to find a solution fitting the preconditions. We distinguish between ‘cheap’ and ‘expensive’ reinsurance which lead to different types of optimal strategies. We obtain explicit expressions for the optimiser and conclude that the optimal strategy is an increasing function of the current drawdown. In particular, the retention level optimally chosen for a zero drawdown is
![]() $b_t=0$
. Section 5 contains a numerical example. The depicted plots of the value function and optimal strategy illustrate the influence of the reinsurance premium. In Section 6 we make some concluding remarks related to the results. We come to the conclusion that the strategy which minimises the expected time with a large drawdown succeeds in stabilising the paths of the surplus process. However, it also prevents growth of the running maximum. Hence, basing operational decisions purely on the prevention of drawdowns will lead to a ‘non-economic’ result. We thus suggest alternatives to extend the optimisation problem for future research.
$b_t=0$
. Section 5 contains a numerical example. The depicted plots of the value function and optimal strategy illustrate the influence of the reinsurance premium. In Section 6 we make some concluding remarks related to the results. We come to the conclusion that the strategy which minimises the expected time with a large drawdown succeeds in stabilising the paths of the surplus process. However, it also prevents growth of the running maximum. Hence, basing operational decisions purely on the prevention of drawdowns will lead to a ‘non-economic’ result. We thus suggest alternatives to extend the optimisation problem for future research.
2. The problem in the absence of reinsurance
We first consider the problem without the possibility of reinsuring the claims. This is equivalent to the case where we look for a static reinsurance treaty. Let
![]() $u(x) = {\mathbb{E}}^{x}[ \int_{0}^{\infty} \textrm{e}^{-\delta t} \textbf{1}_{\{ D_{t}>d\}}\,\textrm{d} t]$
, where D is the drawdown process of the diffusion approximation (1.1). This function is positive and bounded by
$u(x) = {\mathbb{E}}^{x}[ \int_{0}^{\infty} \textrm{e}^{-\delta t} \textbf{1}_{\{ D_{t}>d\}}\,\textrm{d} t]$
, where D is the drawdown process of the diffusion approximation (1.1). This function is positive and bounded by
![]() $\delta^{-1}$
. It is non-decreasing in x and, by bounded convergence, the function u(x) converges to
$\delta^{-1}$
. It is non-decreasing in x and, by bounded convergence, the function u(x) converges to
![]() $\delta^{-1}$
as
$\delta^{-1}$
as
![]() $x \to \infty$
. If u was twice continuously differentiable we could use Itô’s formula to find
$x \to \infty$
. If u was twice continuously differentiable we could use Itô’s formula to find
where we define
![]() $\mathfrak{A}f \,{:\!=}\, - \delta f-\eta f' + \frac{\sigma^{2}}{2} f''$
. Since
$\mathfrak{A}f \,{:\!=}\, - \delta f-\eta f' + \frac{\sigma^{2}}{2} f''$
. Since
![]() $\overline{X}$
increases at times where
$\overline{X}$
increases at times where
![]() $D=\overline{X} -X =0 $
, we can replace
$D=\overline{X} -X =0 $
, we can replace
![]() $u'(D_{s})$
by u
$u'(D_{s})$
by u
![]() $^{\prime}$
(0) in the last expression. If the drawdown process is much closer to zero than it is to the critical boundary, there is a high probability that it reaches zero before exiting the interval. Intuitively, this means that the time the process spends in the critical area is very close to the time a process starting at zero spends in the critical area. If we assume, based on this intuition, that
$^{\prime}$
(0) in the last expression. If the drawdown process is much closer to zero than it is to the critical boundary, there is a high probability that it reaches zero before exiting the interval. Intuitively, this means that the time the process spends in the critical area is very close to the time a process starting at zero spends in the critical area. If we assume, based on this intuition, that
![]() $u'(0)=0$
is fulfilled, the last integral vanishes. Taking the expected value and assuming for a moment that the stochastic integral is a martingale, we arrive at
$u'(0)=0$
is fulfilled, the last integral vanishes. Taking the expected value and assuming for a moment that the stochastic integral is a martingale, we arrive at
![]() $u(x) =- {\mathbb{E}}^{x}\bigl[ \int_{0}^{t} \textrm{e}^{-\delta s} \mathfrak{A}u(D_{s}) \,\textrm{d} s \bigr] + {\mathbb{E}}^{x}[ \textrm{e}^{-\delta t} u(D_{t})]$
. Since u is bounded, the last term converges to zero as
$u(x) =- {\mathbb{E}}^{x}\bigl[ \int_{0}^{t} \textrm{e}^{-\delta s} \mathfrak{A}u(D_{s}) \,\textrm{d} s \bigr] + {\mathbb{E}}^{x}[ \textrm{e}^{-\delta t} u(D_{t})]$
. Since u is bounded, the last term converges to zero as
![]() $t \to\infty$
. Letting
$t \to\infty$
. Letting
![]() $t \to \infty$
, we find
$t \to \infty$
, we find
![]() $u(x) = {\mathbb{E}}^{x}\bigl[ \int_{0}^{\infty} \textrm{e}^{-\delta s} (-\mathfrak{A}u(D_{s}) )\,\textrm{d} s \bigr]$
. We therefore presume that u is a solution to
$u(x) = {\mathbb{E}}^{x}\bigl[ \int_{0}^{\infty} \textrm{e}^{-\delta s} (-\mathfrak{A}u(D_{s}) )\,\textrm{d} s \bigr]$
. We therefore presume that u is a solution to
![]() $\mathfrak{A} u(x) = -\textbf{1}_{\{ x >d \}} $
with
$\mathfrak{A} u(x) = -\textbf{1}_{\{ x >d \}} $
with
![]() $u'(0)=0$
and
$u'(0)=0$
and
![]() $u(0)> 0$
. The homogeneous equation
$u(0)> 0$
. The homogeneous equation
![]() $\mathfrak{A} u(x)=0$
has solutions of the form
$\mathfrak{A} u(x)=0$
has solutions of the form
![]() $f_{0}(x) = C_{1} \textrm{e}^{-\kappa x} + C_{2} \textrm{e}^{\check{\kappa} x}$
, where
$f_{0}(x) = C_{1} \textrm{e}^{-\kappa x} + C_{2} \textrm{e}^{\check{\kappa} x}$
, where
By
![]() $u'(0)=0$
,
$u'(0)=0$
,
![]() $C_{1}=u(0) \frac{\check{\kappa}}{\check{\kappa} + \kappa}$
and
$C_{1}=u(0) \frac{\check{\kappa}}{\check{\kappa} + \kappa}$
and
![]() $C_{2} =u(0) \frac{\kappa}{\check{\kappa} + \kappa}> 0.$
As the constant function
$C_{2} =u(0) \frac{\kappa}{\check{\kappa} + \kappa}> 0.$
As the constant function
![]() $x \mapsto \delta^{-1}$
solves the inhomogeneous equation
$x \mapsto \delta^{-1}$
solves the inhomogeneous equation
![]() $\mathfrak{A} u(x)=-1$
, we look for a smooth fit at
$\mathfrak{A} u(x)=-1$
, we look for a smooth fit at
![]() $x = d$
. This yields
$x = d$
. This yields
As
![]() $f_{1}(x)$
is supposed to converge to
$f_{1}(x)$
is supposed to converge to
![]() $\delta^{-1}$
as x tends to infinity and
$\delta^{-1}$
as x tends to infinity and
![]() $\check{\kappa}$
is strictly positive, we need
$\check{\kappa}$
is strictly positive, we need
![]() $1=\delta u(0)\textrm{e}^{\check{\kappa} d}$
. This can only hold if
$1=\delta u(0)\textrm{e}^{\check{\kappa} d}$
. This can only hold if
![]() $u(0)=\delta^{-1} \textrm{e}^{-\check{\kappa}d}$
. Combining the piecewise solutions and plugging in all the constants, we find a candidate solution:
$u(0)=\delta^{-1} \textrm{e}^{-\check{\kappa}d}$
. Combining the piecewise solutions and plugging in all the constants, we find a candidate solution:
 \begin{equation}f(x) = \begin{cases} \dfrac{\kappa \textrm{e}^{\check{\kappa} x} +\check{\kappa}\textrm{e}^{-\kappa x} }{\delta \textrm{e}^{\check{\kappa}d} (\kappa +\check{\kappa})} , & \text{if }x \leq d , \\ \\[-7pt] \dfrac{1}{\delta} -\frac{1}{\delta}\frac{\check{\kappa}}{\kappa+\check{\kappa}}(\textrm{e}^{\kappa d} - \textrm{e}^{-\check{\kappa} d}) \textrm{e}^{-\kappa x} , & \text{if } x>d. \end{cases}\end{equation}
\begin{equation}f(x) = \begin{cases} \dfrac{\kappa \textrm{e}^{\check{\kappa} x} +\check{\kappa}\textrm{e}^{-\kappa x} }{\delta \textrm{e}^{\check{\kappa}d} (\kappa +\check{\kappa})} , & \text{if }x \leq d , \\ \\[-7pt] \dfrac{1}{\delta} -\frac{1}{\delta}\frac{\check{\kappa}}{\kappa+\check{\kappa}}(\textrm{e}^{\kappa d} - \textrm{e}^{-\check{\kappa} d}) \textrm{e}^{-\kappa x} , & \text{if } x>d. \end{cases}\end{equation}
Theorem 2.1. The function (2.1) is indeed the value function.
Proof. The function f(x) is the difference of two convex functions and everywhere twice continuously differentiable, except at
![]() $x=d$
, where the second derivatives do not coincide. This allows us to apply an extended version of the Itô- formula [Reference Elworthy, Truman and Zhao8, Theorem 2.1 and Eq. (2.23)] to the function
$x=d$
, where the second derivatives do not coincide. This allows us to apply an extended version of the Itô- formula [Reference Elworthy, Truman and Zhao8, Theorem 2.1 and Eq. (2.23)] to the function
![]() $(t,x ) \mapsto \textrm{e}^{-\delta t} f(x)$
and the continuous semimartingale
$(t,x ) \mapsto \textrm{e}^{-\delta t} f(x)$
and the continuous semimartingale
![]() $\lbrace (t, D_t)\rbrace_{t\geq 0 }$
:
$\lbrace (t, D_t)\rbrace_{t\geq 0 }$
:
By
![]() $f'(0)=0$
, the first integral disappears. Because f is increasing and concave for
$f'(0)=0$
, the first integral disappears. Because f is increasing and concave for
![]() $x>d$
, the derivative is bounded. Hence, the stochastic integral is a martingale. This implies that the process
$x>d$
, the derivative is bounded. Hence, the stochastic integral is a martingale. This implies that the process
![]() $\bigl\{ \textrm{e}^{-\delta t} f(D_t) - \int_0^t \textrm{e}^{-\delta s} \mathfrak{A} f(D_s)\,\textrm{d} s\bigr\}_{t\geq 0}$
is also a martingale. Therefore,
$\bigl\{ \textrm{e}^{-\delta t} f(D_t) - \int_0^t \textrm{e}^{-\delta s} \mathfrak{A} f(D_s)\,\textrm{d} s\bigr\}_{t\geq 0}$
is also a martingale. Therefore,
![]() $ f(x) = {\mathbb{E}}^{x}[\textrm{e}^{-\delta t} f(D_t)] + {\mathbb{E}}^{x}\bigl[\int_0^t \textrm{e}^{-\delta s}\textbf{1}_{\{ D_s > d \}} \,\textrm{d} s \bigr]$
. Since f is bounded, the first expected value tends to zero as
$ f(x) = {\mathbb{E}}^{x}[\textrm{e}^{-\delta t} f(D_t)] + {\mathbb{E}}^{x}\bigl[\int_0^t \textrm{e}^{-\delta s}\textbf{1}_{\{ D_s > d \}} \,\textrm{d} s \bigr]$
. Since f is bounded, the first expected value tends to zero as
![]() $t \to\infty$
. The assertion follows by monotone convergence.
$t \to\infty$
. The assertion follows by monotone convergence.
3. Solution and verification for
 $\textbf{x}\,{>}\, \textbf{d}$
$\textbf{x}\,{>}\, \textbf{d}$
We now look for the optimal reinsurance strategy b when starting in the drawdown region. As seen in the introduction, we have to find a strategy that maximises the Laplace transform
![]() $V^b(x) = {\mathbb{E}} [\textrm{e}^{-\delta \vartheta (b)}]$
of the passage through d. Let
$V^b(x) = {\mathbb{E}} [\textrm{e}^{-\delta \vartheta (b)}]$
of the passage through d. Let
![]() $V(x) = \sup_b V^b(x)$
. Since the drift component is a decreasing function of the retention level, the retention level leading to the largest downward trend,
$V(x) = \sup_b V^b(x)$
. Since the drift component is a decreasing function of the retention level, the retention level leading to the largest downward trend,
![]() $b_t=1$
, should intuitively be optimal. We now prove that this is indeed the case. In order to reach d, the drawdown has to pass all levels
$b_t=1$
, should intuitively be optimal. We now prove that this is indeed the case. In order to reach d, the drawdown has to pass all levels
![]() $y \in (d,x)$
. Conditioning on the time of reaching a certain level y, we obtain
$y \in (d,x)$
. Conditioning on the time of reaching a certain level y, we obtain
![]() ${\mathbb{E}}^x [\textrm{e}^{-\delta \vartheta (b)}] = {\mathbb{E}}^x \big[\textrm{e}^{-\delta \vartheta_y(b)} {\mathbb{E}}^y\big[\textrm{e}^{-\delta \vartheta (\tilde b)} \mid \mathcal{{F}}_{\vartheta_y(b)}\big]\big] \le {\mathbb{E}}^x\big[\textrm{e}^{-\delta \vartheta_y(b)}\big] V(x-y+d) \le V(y) V(x-y+d)$
. Thus,
${\mathbb{E}}^x [\textrm{e}^{-\delta \vartheta (b)}] = {\mathbb{E}}^x \big[\textrm{e}^{-\delta \vartheta_y(b)} {\mathbb{E}}^y\big[\textrm{e}^{-\delta \vartheta (\tilde b)} \mid \mathcal{{F}}_{\vartheta_y(b)}\big]\big] \le {\mathbb{E}}^x\big[\textrm{e}^{-\delta \vartheta_y(b)}\big] V(x-y+d) \le V(y) V(x-y+d)$
. Thus,
![]() $V(x) \le V(y) V(x-y+d)$
. Moreover,
$V(x) \le V(y) V(x-y+d)$
. Moreover,
![]() $V(x) \ge {\mathbb{E}}^x \big[\textrm{e}^{-\delta \vartheta_y(b)} {\mathbb{E}}^y\big[\textrm{e}^{-\delta \vartheta (\tilde b)}\mid \mathcal{{F}}_{\vartheta_y(b)}\big]\big]$
, and maximising first over
$V(x) \ge {\mathbb{E}}^x \big[\textrm{e}^{-\delta \vartheta_y(b)} {\mathbb{E}}^y\big[\textrm{e}^{-\delta \vartheta (\tilde b)}\mid \mathcal{{F}}_{\vartheta_y(b)}\big]\big]$
, and maximising first over
![]() $\tilde b$
and then over b gives the converse inequality. Thus,
$\tilde b$
and then over b gives the converse inequality. Thus,
![]() $V(x)= V(y) V(x-y+d)$
. This implies that V(x) is an exponential function. On the other hand, split (d,x) into
$V(x)= V(y) V(x-y+d)$
. This implies that V(x) is an exponential function. On the other hand, split (d,x) into
![]() $2^{n}$
parts. In each of the intervals
$2^{n}$
parts. In each of the intervals
![]() $[x_{k-1}, x_k]$
, where
$[x_{k-1}, x_k]$
, where
![]() $x_k = d + k (x-d) 2^{-n}$
, we have to maximise
$x_k = d + k (x-d) 2^{-n}$
, we have to maximise
![]() ${\mathbb{E}}^{x_k}\big[\textrm{e}^{-\delta \vartheta_{x_{k-1}}(b)}\big]$
. This is the same optimisation problem for each k, which indicates that the optimal strategy is constant.
${\mathbb{E}}^{x_k}\big[\textrm{e}^{-\delta \vartheta_{x_{k-1}}(b)}\big]$
. This is the same optimisation problem for each k, which indicates that the optimal strategy is constant.
The Hamilton–Jacobi–Bellman (HJB) equation connected to the problem is
With the ansatz
![]() $V(x) = \textrm{e}^{-\kappa(x-d)}$
, we obtain
$V(x) = \textrm{e}^{-\kappa(x-d)}$
, we obtain
The left-hand side is maximised for
![]() $b = 1$
. Thus, the proposed optimal strategy is
$b = 1$
. Thus, the proposed optimal strategy is
![]() $b_t = 1$
, and
$b_t = 1$
, and
![]() $\kappa$
is defined as in Section 2.
$\kappa$
is defined as in Section 2.
Theorem 3.1.
![]() $V(x) = \textrm{e}^{-\kappa(x-d)}$
for
$V(x) = \textrm{e}^{-\kappa(x-d)}$
for
![]() $x \ge d$
.
$x \ge d$
.
Proof. By Itô’s formula and the optional stopping theorem we get, for an arbitrary strategy b, that
 \begin{equation*} \Biggl\{ \textrm{e}^{-\kappa D_{t\wedge \vartheta_{d}(b)}^{b}-\delta (t \wedge\vartheta_{d}(b))} - \int_{0}^{t\wedge \vartheta_{d}(b)} \biggl[\frac{\kappa^2\sigma^{2}b_{s}^{2}}{2} - \kappa ((1-b_{s}) \theta -\eta) -\delta\biggr]\textrm{e}^{-\kappa D_s^b - \delta s}\,\textrm{d} s \Biggr\}_{t\geq 0}\end{equation*}
\begin{equation*} \Biggl\{ \textrm{e}^{-\kappa D_{t\wedge \vartheta_{d}(b)}^{b}-\delta (t \wedge\vartheta_{d}(b))} - \int_{0}^{t\wedge \vartheta_{d}(b)} \biggl[\frac{\kappa^2\sigma^{2}b_{s}^{2}}{2} - \kappa ((1-b_{s}) \theta -\eta) -\delta\biggr]\textrm{e}^{-\kappa D_s^b - \delta s}\,\textrm{d} s \Biggr\}_{t\geq 0}\end{equation*}
is a martingale. Because the integrand is negative,
![]() ${\mathbb{E}}^{x} \big[\textrm{e}^{-\kappa D_{t\wedge \vartheta_{d}(b)}^{b} -\delta (t \wedge\vartheta_{d}(b))}\big] \leq \textrm{e}^{-\kappa x}$
. By letting
${\mathbb{E}}^{x} \big[\textrm{e}^{-\kappa D_{t\wedge \vartheta_{d}(b)}^{b} -\delta (t \wedge\vartheta_{d}(b))}\big] \leq \textrm{e}^{-\kappa x}$
. By letting
![]() $t \to \infty$
we find that
$t \to \infty$
we find that
![]() ${\mathbb{E}}^{x}\big[\textrm{e}^{-\delta \vartheta_{d}(b)}\big] \leq\textrm{e}^{-\kappa (x-d)}$
. Because the strategy is arbitrary,
${\mathbb{E}}^{x}\big[\textrm{e}^{-\delta \vartheta_{d}(b)}\big] \leq\textrm{e}^{-\kappa (x-d)}$
. Because the strategy is arbitrary,
![]() $V(x) \le \textrm{e}^{-\kappa x}$
. Repeating the argument for
$V(x) \le \textrm{e}^{-\kappa x}$
. Repeating the argument for
![]() $b_t = 1$
we get equality, proving the assertion.
$b_t = 1$
we get equality, proving the assertion.
Suppose v(d) is known; then, we can conclude that
![]() $v(x) = \frac{1}{\delta } \bigl( 1- (1-\delta v(d)) \textrm{e}^{-\kappa (x-d)}\bigr)$
for an initial drawdown of
$v(x) = \frac{1}{\delta } \bigl( 1- (1-\delta v(d)) \textrm{e}^{-\kappa (x-d)}\bigr)$
for an initial drawdown of
![]() $x \geq d$
.
$x \geq d$
.
4. Solution and verification for
 $\textbf{x} \leq \textbf{d}$
$\textbf{x} \leq \textbf{d}$
Now we deal with the problem of minimising the Laplace transform of the time spent in the uncritical area. We define
![]() $V^b(x) = {\mathbb{E}}^{x} \big[\textrm{e}^{-\delta \vartheta(b)}\big]$
for a reinsurance strategy b, and let
$V^b(x) = {\mathbb{E}}^{x} \big[\textrm{e}^{-\delta \vartheta(b)}\big]$
for a reinsurance strategy b, and let
![]() $V(x) = \inf_b V^b(x)$
. It is clear that V is increasing, positive, and bounded by 1. We expect that V is a solution to the HJB equation
$V(x) = \inf_b V^b(x)$
. It is clear that V is increasing, positive, and bounded by 1. We expect that V is a solution to the HJB equation
with the boundary condition
![]() $V(d)=1$
.
$V(d)=1$
.
4.1. The verification theorem
For a twice continuously differentiable solution f(x) to (4.1), an optimiser
![]() $b^*(x)$
exists because [0, 1] is compact. We will see below that the function
$b^*(x)$
exists because [0, 1] is compact. We will see below that the function
![]() $x \mapsto b^*(x)$
can be chosen measurably. We denote the drawdown process under the strategy
$x \mapsto b^*(x)$
can be chosen measurably. We denote the drawdown process under the strategy
![]() $\{b^*(D_t^{b^*})\}$
induced by the function
$\{b^*(D_t^{b^*})\}$
induced by the function
![]() $b^\ast(x)$
by
$b^\ast(x)$
by
![]() $\{D^*_t\}$
, and the running maximum by
$\{D^*_t\}$
, and the running maximum by
![]() $\{ \overline{X^\ast_t}\}$
.
$\{ \overline{X^\ast_t}\}$
.
Theorem 4.1. Let f(x) be an increasing solution to (4.1) on [0, d]. Then
![]() $f(x) \leq V(x) f(d)$
. If
$f(x) \leq V(x) f(d)$
. If
![]() $f'(0) = 0$
or the running maximum process never increases, then
$f'(0) = 0$
or the running maximum process never increases, then
![]() $f(x) = V(x) f(d)$
and
$f(x) = V(x) f(d)$
and
![]() $\{b^*(D_t^*)\}$
is an optimal strategy.
$\{b^*(D_t^*)\}$
is an optimal strategy.
Proof. For an arbitrary strategy b we get, by Itô’s formula,
 \begin{align*} {\textrm{e}^{-\delta (\vartheta_d(b) \wedge{t})} f(D_{\vartheta_d(b) \wedge t}^b) - f(x)} & = \int_0^{\vartheta_d(b) \wedge t} \!\!\! \textrm{e}^{-\delta s} f' (D_s^b) b_s \sigma\,\textrm{d} W_s + \! \int_0^{\vartheta_d(b) \wedge t} \!\!\! \textrm{e}^{-\delta s} \mathfrak{A}^{b_s} f(D_s^b) \,\textrm{d} s\\[3pt] & \quad + \int_0^{\vartheta_d(b) \wedge t} \textrm{e}^{-\delta s} f'(0) \,\textrm{d} \overline{X_s^b} , \end{align*}
\begin{align*} {\textrm{e}^{-\delta (\vartheta_d(b) \wedge{t})} f(D_{\vartheta_d(b) \wedge t}^b) - f(x)} & = \int_0^{\vartheta_d(b) \wedge t} \!\!\! \textrm{e}^{-\delta s} f' (D_s^b) b_s \sigma\,\textrm{d} W_s + \! \int_0^{\vartheta_d(b) \wedge t} \!\!\! \textrm{e}^{-\delta s} \mathfrak{A}^{b_s} f(D_s^b) \,\textrm{d} s\\[3pt] & \quad + \int_0^{\vartheta_d(b) \wedge t} \textrm{e}^{-\delta s} f'(0) \,\textrm{d} \overline{X_s^b} , \end{align*}
where
![]() $\mathfrak{A}^b f(x) = -\delta f(x) +(\theta (1-b) - \eta) f'(x) +\tfrac{1}{2}{b^{2}\sigma^{2}} f''(x)$
. The stochastic integral is a martingale because f
$\mathfrak{A}^b f(x) = -\delta f(x) +(\theta (1-b) - \eta) f'(x) +\tfrac{1}{2}{b^{2}\sigma^{2}} f''(x)$
. The stochastic integral is a martingale because f
![]() $^{\prime}$
(x) is bounded on [0, d]. As a solution to (4.1),
$^{\prime}$
(x) is bounded on [0, d]. As a solution to (4.1),
![]() $\mathfrak{A}^{b_s} f(D_s^b) \ge 0$
. As an increasing function,
$\mathfrak{A}^{b_s} f(D_s^b) \ge 0$
. As an increasing function,
![]() $f'(0) \ge 0$
. Thus,
$f'(0) \ge 0$
. Thus,
![]() $f(x) \leq{\mathbb{E}}\big[\textrm{e}^{-\delta (\vartheta_d(b) \wedge t)}f(D_{\vartheta_d(b) \wedge t}^b)\big]$
. By monotone convergence, the right-hand side converges to
$f(x) \leq{\mathbb{E}}\big[\textrm{e}^{-\delta (\vartheta_d(b) \wedge t)}f(D_{\vartheta_d(b) \wedge t}^b)\big]$
. By monotone convergence, the right-hand side converges to
![]() $V^b(x) f(d)$
as
$V^b(x) f(d)$
as
![]() $t \to \infty$
. Thus,
$t \to \infty$
. Thus,
![]() $f(x) \leq V(x)f(d)$
. Choosing the strategy
$f(x) \leq V(x)f(d)$
. Choosing the strategy
![]() $\{b^*(D_t^*)\}$
, we get
$\{b^*(D_t^*)\}$
, we get
![]() $f(x) = V^{b^*}(x) f(x) - f'(0){\mathbb{E}}\big[\int_0^{\vartheta_d(b^*)} \textrm{e}^{-\delta s} \,\textrm{d} \overline{X_s^{b^*}}\big]$
. The second term vanishes if either
$f(x) = V^{b^*}(x) f(x) - f'(0){\mathbb{E}}\big[\int_0^{\vartheta_d(b^*)} \textrm{e}^{-\delta s} \,\textrm{d} \overline{X_s^{b^*}}\big]$
. The second term vanishes if either
![]() $f'(0) = 0$
or
$f'(0) = 0$
or
![]() $X^*$
does not increase (almost surely). In these cases, we thus get the opposite inequality.
$X^*$
does not increase (almost surely). In these cases, we thus get the opposite inequality.
4.2. Solution to the HJB equation
To calculate an explicit solution to the HJB equation we analyse the optimiser b. Since V is increasing, the last part of (4.1) becomes minimal for
![]() $b=1$
at every x with
$b=1$
at every x with
![]() $V''(x) \leq 0$
. The following lemma shows that this is only possible if
$V''(x) \leq 0$
. The following lemma shows that this is only possible if
![]() $V \equiv 0$
up to x.
$V \equiv 0$
up to x.
Lemma 4.1. If
![]() $V\,{:}\,(0, d) \to [0,1]$
is an increasing solution to (4.1) and
$V\,{:}\,(0, d) \to [0,1]$
is an increasing solution to (4.1) and
![]() $V''(x) \leq 0$
in some interval
$V''(x) \leq 0$
in some interval
![]() $(\underline{x}, \overline{x}) \subset (0, d)$
, then
$(\underline{x}, \overline{x}) \subset (0, d)$
, then
![]() $V(x) = 0$
in
$V(x) = 0$
in
![]() $(0, \overline{x})$
.
$(0, \overline{x})$
.
Proof. If
![]() $V''(x) \leq 0$
in an interval
$V''(x) \leq 0$
in an interval
![]() $(\underline{x}, \overline{x}) \subset (0,d)$
, then the infimum in (4.1) is attained at
$(\underline{x}, \overline{x}) \subset (0,d)$
, then the infimum in (4.1) is attained at
![]() $b^*=1$
. The equation then reads
$b^*=1$
. The equation then reads
![]() $0 =-\delta V(x)-\eta V'(x) + \tfrac{1}{2}{\sigma^{2}} V''(x)$
. The solution is of the form
$0 =-\delta V(x)-\eta V'(x) + \tfrac{1}{2}{\sigma^{2}} V''(x)$
. The solution is of the form
![]() $V(x) = C_{1} \textrm{e}^{\check{\kappa} x} - C_{2}\textrm{e}^{-\kappa x}$
, with
$V(x) = C_{1} \textrm{e}^{\check{\kappa} x} - C_{2}\textrm{e}^{-\kappa x}$
, with
![]() $\kappa$
and
$\kappa$
and
![]() $\check{\kappa}$
defined above. The second derivative reads
$\check{\kappa}$
defined above. The second derivative reads
![]() $V''(x) = C_{1} {\check{\kappa}}^{2}\textrm{e}^{\check{\kappa} x} - C_{2}\kappa^{2}\textrm{e}^{-\kappa x} \leq 0$
, such that
$V''(x) = C_{1} {\check{\kappa}}^{2}\textrm{e}^{\check{\kappa} x} - C_{2}\kappa^{2}\textrm{e}^{-\kappa x} \leq 0$
, such that
On the other hand, since
![]() $V(x) \geq 0$
,
$V(x) \geq 0$
,
![]() $C_{1} \textrm{e}^{(\check{\kappa}+\kappa)x} \geq C_{2}$
, giving
$C_{1} \textrm{e}^{(\check{\kappa}+\kappa)x} \geq C_{2}$
, giving
Since
![]() $\check{\kappa}\kappa^{-1}>1$
, this that implies
$\check{\kappa}\kappa^{-1}>1$
, this that implies
![]() $C_{1} \le 0$
and
$C_{1} \le 0$
and
![]() $C_{2} \le 0 $
. Then we have, for the derivative,
$C_{2} \le 0 $
. Then we have, for the derivative,
![]() $C_1 \check\kappa \textrm{e}^{\check\kappa x} + C_2 \kappa \textrm{e}^{-\kappa x} \le0$
. Since the function is increasing, we must have
$C_1 \check\kappa \textrm{e}^{\check\kappa x} + C_2 \kappa \textrm{e}^{-\kappa x} \le0$
. Since the function is increasing, we must have
![]() $C_1 = C_2 = 0$
. This yields the assertion.
$C_1 = C_2 = 0$
. This yields the assertion.
In view of Lemma 4.1 we expect that V is strictly convex in (0, d). Minimising over b in (4.1) yields, in the area where
![]() $b^* \ne 1$
,
$b^* \ne 1$
,
We follow the approach in [Reference Højgaard and Taksar11]. The function
![]() $x \mapsto -\ln(V'(x))$
is strictly decreasing and therefore has an inverse function Y. With this definition we have
$x \mapsto -\ln(V'(x))$
is strictly decreasing and therefore has an inverse function Y. With this definition we have
![]() $V'(Y(z))= \textrm{e}^{-z}$
and
$V'(Y(z))= \textrm{e}^{-z}$
and
![]() $V''(Y(z)) = -\textrm{e}^{-z} /Y'(z)$
. Inserting this into (4.2), we find
$V''(Y(z)) = -\textrm{e}^{-z} /Y'(z)$
. Inserting this into (4.2), we find
Taking the derivative respect to z yields
or equivalently,
The general solution is
![]() $Y(z) = C_{1} \textrm{e}^{B z } - D z - C_{2}$
, with
$Y(z) = C_{1} \textrm{e}^{B z } - D z - C_{2}$
, with
![]() $B\,{:\!=}\, (2\delta \sigma^{2}+\theta^{2})\theta^{-2}> 1 $
and
$B\,{:\!=}\, (2\delta \sigma^{2}+\theta^{2})\theta^{-2}> 1 $
and
![]() $D\,{:\!=}\, 2\sigma^{2}(\theta-\eta) (2 \delta \sigma^{2}+ \theta^{2} )^{-1}$
. In a martingale approach, the reflection in zero implies that
$D\,{:\!=}\, 2\sigma^{2}(\theta-\eta) (2 \delta \sigma^{2}+ \theta^{2} )^{-1}$
. In a martingale approach, the reflection in zero implies that
![]() $V'(0) = 0$
, unless X never reaches a level above d under the optimal strategy. But if we assume that the derivative is zero,
$V'(0) = 0$
, unless X never reaches a level above d under the optimal strategy. But if we assume that the derivative is zero,
![]() $V'(Y(z))=\textrm{e}^{-z}=0$
implies
$V'(Y(z))=\textrm{e}^{-z}=0$
implies
![]() $z=\infty$
and
$z=\infty$
and
![]() $Y(\infty )=0$
. This is not possible because
$Y(\infty )=0$
. This is not possible because
![]() $B, D >0$
. Conclusively, we expect that the process X never reaches
$B, D >0$
. Conclusively, we expect that the process X never reaches
![]() $(d,\infty)$
. This is only possible if
$(d,\infty)$
. This is only possible if
![]() $b^*(x)=\frac{\theta V'(x)}{\sigma^{2}V''(x)}\to 0$
as
$b^*(x)=\frac{\theta V'(x)}{\sigma^{2}V''(x)}\to 0$
as
![]() $x \to 0$
. In particular,
$x \to 0$
. In particular,
![]() $V''(0) = \infty$
and
$V''(0) = \infty$
and
![]() $V'(0) = V(0)\frac{\delta}{\theta -\eta}$
. Therefore, with
$V'(0) = V(0)\frac{\delta}{\theta -\eta}$
. Therefore, with
![]() $z_{0}\,{:\!=}\,\ln((\theta -\eta)\delta^{-1} V(0)^{-1})$
, we have
$z_{0}\,{:\!=}\,\ln((\theta -\eta)\delta^{-1} V(0)^{-1})$
, we have
![]() $Y(z_{0}) = 0$
and
$Y(z_{0}) = 0$
and
![]() $Y'(z_{0})=0$
. With these initial conditions we find the convex solution
$Y'(z_{0})=0$
. With these initial conditions we find the convex solution
![]() $Y(z)=\frac{D}{B} \textrm{e}^{B (z -z_{0}) } - D (z-z_{0}) -\frac{D}{B}$
, which has the properties
$Y(z)=\frac{D}{B} \textrm{e}^{B (z -z_{0}) } - D (z-z_{0}) -\frac{D}{B}$
, which has the properties
![]() $Y'(z)<0$
for
$Y'(z)<0$
for
![]() $z<z_{0}$
and
$z<z_{0}$
and
![]() $Y(z)\to \infty$
as
$Y(z)\to \infty$
as
![]() $z\to - \infty$
. For every
$z\to - \infty$
. For every
![]() $y>0$
there exists a unique
$y>0$
there exists a unique
![]() $z<z_{0}$
such that
$z<z_{0}$
such that
![]() $Y(z) = y$
. Let
$Y(z) = y$
. Let
![]() $Z(y) = Y^{-1}(y)$
be the corresponding part of the inverse function. Z(y) is decreasing, because Y is decreasing on
$Z(y) = Y^{-1}(y)$
be the corresponding part of the inverse function. Z(y) is decreasing, because Y is decreasing on
![]() $(-\infty, z_{0})$
. We can write Z in terms of the upper branch
$(-\infty, z_{0})$
. We can write Z in terms of the upper branch
![]() $\textsf{W}_{\textsf{0}}$
of the Lambert
$\textsf{W}_{\textsf{0}}$
of the Lambert
![]() $\textsf{W}$
function:
$\textsf{W}$
function:
Then,
and
We can calculate V by substituting
![]() $w(y)=-\textsf{W}_{\textsf{0}}(-\exp(-(1+BD^{-1} y)))$
in the integral term. Plugging in the definitions of
$w(y)=-\textsf{W}_{\textsf{0}}(-\exp(-(1+BD^{-1} y)))$
in the integral term. Plugging in the definitions of
![]() $z_{0}$
, B, and D, we find
$z_{0}$
, B, and D, we find
 \begin{align*} \int_0^x \textrm{e}^{-Z(y)} \,\textrm{d} y & = \textrm{e}^{-z_{0}}\frac{D}{B} \int_{\exp\{-(1+Bx/D)\}}^{\textrm{e}^{-1}} v^{-(1+B^{-1})} \textrm{e}^{W_0(-v)/B} \,\textrm{d} v \\[3pt] & = \textrm{e}^{-z_{0}}\frac{D}{B}\int_{w(x)}^1 (1-w) w^{-(1+B^{-1})} \,\textrm{d} w \\[3pt] & = \frac{V(0)}{2 \delta \sigma^2 + \theta^2}\Bigl[\{ 2 \delta \sigma^2 +\theta^2 w(x)\}w(x)^{-\theta^{2}/(2\delta \sigma^{2}+\theta^{2})} - (2 \delta \sigma^2 + \theta^2)\Bigr]. \end{align*}
\begin{align*} \int_0^x \textrm{e}^{-Z(y)} \,\textrm{d} y & = \textrm{e}^{-z_{0}}\frac{D}{B} \int_{\exp\{-(1+Bx/D)\}}^{\textrm{e}^{-1}} v^{-(1+B^{-1})} \textrm{e}^{W_0(-v)/B} \,\textrm{d} v \\[3pt] & = \textrm{e}^{-z_{0}}\frac{D}{B}\int_{w(x)}^1 (1-w) w^{-(1+B^{-1})} \,\textrm{d} w \\[3pt] & = \frac{V(0)}{2 \delta \sigma^2 + \theta^2}\Bigl[\{ 2 \delta \sigma^2 +\theta^2 w(x)\}w(x)^{-\theta^{2}/(2\delta \sigma^{2}+\theta^{2})} - (2 \delta \sigma^2 + \theta^2)\Bigr]. \end{align*}
Thus, we conclude that
It will be useful to know the following simplified version of the derivative:
 \begin{equation*} V'(x) = \textrm{e}^{-Z(x)} = V(0)\frac{\delta}{(\theta-\eta) w(x)^{\frac{\theta^{2}}{2\delta\sigma^{2}+\theta^{2}}}}. \end{equation*}
\begin{equation*} V'(x) = \textrm{e}^{-Z(x)} = V(0)\frac{\delta}{(\theta-\eta) w(x)^{\frac{\theta^{2}}{2\delta\sigma^{2}+\theta^{2}}}}. \end{equation*}
4.3. The optimal strategy
The considerations above are under the condition that
![]() $b(x)=\frac{\theta V'(x)}{\sigma^{2} V''(x)} \le 1$
. We have, on the one hand, to verify that
$b(x)=\frac{\theta V'(x)}{\sigma^{2} V''(x)} \le 1$
. We have, on the one hand, to verify that
![]() $b(x)\le 1$
at least for
$b(x)\le 1$
at least for
![]() $x \in [0,x_0\wedge d)$
for some
$x \in [0,x_0\wedge d)$
for some
![]() $x_0 > 0$
. On the other hand, we have to determine the optimal retention level for
$x_0 > 0$
. On the other hand, we have to determine the optimal retention level for
![]() $x \ge x_0\wedge d$
. We expect that no reinsurance is taken for a drawdown of
$x \ge x_0\wedge d$
. We expect that no reinsurance is taken for a drawdown of
![]() $x \in [x_0 \wedge d,\infty)$
.
$x \in [x_0 \wedge d,\infty)$
.
The optimiser of the solution V of (4.1) is
This is strictly increasing and
![]() $x \mapsto\sqrt{x}$
is an asymptotically sharp bound for
$x \mapsto\sqrt{x}$
is an asymptotically sharp bound for
![]() $x \to 0$
. Our candidate for the optimal strategy is therefore
$x \to 0$
. Our candidate for the optimal strategy is therefore
w(x) is a decreasing function,
![]() $w(x) \nearrow 1$
as
$w(x) \nearrow 1$
as
![]() $x \searrow 0$
, and
$x \searrow 0$
, and
![]() $w(x) \to 0$
as
$w(x) \to 0$
as
![]() $x \to \infty$
. This means that b(x) is increasing and
$x \to \infty$
. This means that b(x) is increasing and
![]() $b(x)\searrow 0$
as
$b(x)\searrow 0$
as
![]() $x\searrow 0$
, as expected, and
$x\searrow 0$
, as expected, and
![]() $b(x) \nearrow\frac{2\theta(\theta-\eta)}{2\delta \sigma^{2}+ \theta^{2}}$
as
$b(x) \nearrow\frac{2\theta(\theta-\eta)}{2\delta \sigma^{2}+ \theta^{2}}$
as
![]() $x\nearrow\infty$
. In particular, the calculated function is a solution to the HJB equation with optimiser
$x\nearrow\infty$
. In particular, the calculated function is a solution to the HJB equation with optimiser
![]() $\tilde{b}$
on [0, d] for all
$\tilde{b}$
on [0, d] for all
![]() $d>0$
if
$d>0$
if
![]() $2 \theta (\theta-\eta) \le 2\delta \sigma^2 + \theta^2$
or, equivalently,
$2 \theta (\theta-\eta) \le 2\delta \sigma^2 + \theta^2$
or, equivalently,
![]() $\theta \leq\eta+\sqrt{2\delta\sigma^{2}+\eta^{2}}$
. If the latter condition is not fulfilled, then we have a solution for
$\theta \leq\eta+\sqrt{2\delta\sigma^{2}+\eta^{2}}$
. If the latter condition is not fulfilled, then we have a solution for
![]() $x \le x_0$
, with
$x \le x_0$
, with
From this equation,
![]() $x_0$
can be calculated explicitly:
$x_0$
can be calculated explicitly:
We have found a solution to the HJB equation for
![]() $\theta \leq\eta+\sqrt{2\delta\sigma^{2}+\eta^{2}}$
and
$\theta \leq\eta+\sqrt{2\delta\sigma^{2}+\eta^{2}}$
and
![]() $\theta >\eta+\sqrt{2\delta\sigma^{2}+\eta^{2}}$
with
$\theta >\eta+\sqrt{2\delta\sigma^{2}+\eta^{2}}$
with
![]() $d \le x_0$
. We expect that b(x) induces an optimal strategy.
$d \le x_0$
. We expect that b(x) induces an optimal strategy.
Remark 4.1. Note that b(x) does not depend on d. This is plausible because for
![]() $x < \tilde d < d$
, the strategy first minimises
$x < \tilde d < d$
, the strategy first minimises
![]() ${\mathbb{E}}^x\big[\textrm{e}^{-\delta\vartheta^{\tilde d}(b)}\big]$
and then
${\mathbb{E}}^x\big[\textrm{e}^{-\delta\vartheta^{\tilde d}(b)}\big]$
and then
![]() ${\mathbb{E}}^{\tilde d}\big[\textrm{e}^{-\delta\vartheta^{d}(b)}\big]$
.
${\mathbb{E}}^{\tilde d}\big[\textrm{e}^{-\delta\vartheta^{d}(b)}\big]$
.
Remark 4.2. Note that
![]() $\theta > \eta+\sqrt{2\delta\sigma^{2}+\eta^{2}} > 2 \eta$
means that reinsurance is very expensive. We do not consider this as a realistic situation. Now that b(x) is explicitly given we can prove the following lemma.
$\theta > \eta+\sqrt{2\delta\sigma^{2}+\eta^{2}} > 2 \eta$
means that reinsurance is very expensive. We do not consider this as a realistic situation. Now that b(x) is explicitly given we can prove the following lemma.
Lemma 4.2. Under the strategy
![]() $\{ b(D^\ast_t) \}_t$
induced by the function b(x) the running maximum is constant.
$\{ b(D^\ast_t) \}_t$
induced by the function b(x) the running maximum is constant.
Proof. The stochastic differential equation
possesses a unique strong solution. This follows by Theorem 2.2 together with Remark 2.1 in [Reference Ikeda and Watanabe12] and [Reference Yamada19, Example 1.1]. We can show that this solution is non-negative for
![]() $Y_0 \geq 0$
by the comparison theorem [Reference Ikeda and Watanabe12, Theorem 1.1]. Now we define the process
$Y_0 \geq 0$
by the comparison theorem [Reference Ikeda and Watanabe12, Theorem 1.1]. Now we define the process
![]() $X^Y$
through
$X^Y$
through
Then, the process M with
![]() $M_t^Y = X_t^Y+Y_t$
,
$M_t^Y = X_t^Y+Y_t$
,
![]() $t\geq 0$
, is constant and equal to zero. Writing
$t\geq 0$
, is constant and equal to zero. Writing
![]() $Y_t = M_t^Y - X_t^Y$
, we observe that, for every path, the pair
$Y_t = M_t^Y - X_t^Y$
, we observe that, for every path, the pair
![]() $\big( Y_t(\omega)$
,
$\big( Y_t(\omega)$
,
![]() $ M_t^Y(\omega)\big)$
is a solution to the Skorokhod problem for
$ M_t^Y(\omega)\big)$
is a solution to the Skorokhod problem for
![]() $ - X_t^Y(\omega)$
. By the uniqueness of solutions to the Skorokhod problem,
$ - X_t^Y(\omega)$
. By the uniqueness of solutions to the Skorokhod problem,
![]() $M^Y$
is the running maximum process and Y the drawdown of
$M^Y$
is the running maximum process and Y the drawdown of
![]() $X^Y$
where the process has an initial distance
$X^Y$
where the process has an initial distance
![]() $Y_0$
to its running maximum. For
$Y_0$
to its running maximum. For
![]() $Y_0=x$
it follows that
$Y_0=x$
it follows that
![]() $Y= D^\ast$
,
$Y= D^\ast$
,
![]() $X^Y=X^\ast-x$
, and
$X^Y=X^\ast-x$
, and
![]() $M= \overline{X^\ast}-x$
.
$M= \overline{X^\ast}-x$
.
Remark 4.3. The discerning reader may comment at this point that the ‘optimal’ control of the time in drawdown prevents the increase of the surplus process above a certain level and thus naturally limits the profitability. We address this observation and its economical implications in Section 6.
It follows from the verification theorem, Theorem 4.1, that the solution V belonging to the optimiser in (4.4) is the value function for our subproblem of maximising the time in uncritical drawdown. We can calculate V explicitly, distinguishing the cases of cheap and expensive reinsurance.
4.4. The case
 $\theta \leq \eta +\sqrt{2\delta \sigma^{2} +\eta^{2}}$
or
$\theta \leq \eta +\sqrt{2\delta \sigma^{2} +\eta^{2}}$
or
 $\boldsymbol{d}\leq \boldsymbol{x}_{\textbf{0}}$
$\boldsymbol{d}\leq \boldsymbol{x}_{\textbf{0}}$
In this case, the optimiser for
![]() $x\in (0, d]$
is given by b(x). Since
$x\in (0, d]$
is given by b(x). Since
![]() $V(d)=1$
, we obtain
$V(d)=1$
, we obtain
Because V(x) is an increasing solution to the HJB equation (4.1), we have proved the following result.
Theorem 4.2. Suppose
![]() $\theta \leq \eta +\sqrt{2\delta \sigma^{2} +\eta^{2}}$
or
$\theta \leq \eta +\sqrt{2\delta \sigma^{2} +\eta^{2}}$
or
![]() $d\leq x_{0}$
. Then
$d\leq x_{0}$
. Then
The strategy
![]() $\{ b(D^\ast_t) \}_t$
is the optimal strategy.
$\{ b(D^\ast_t) \}_t$
is the optimal strategy.
Let us return to our original problem. By the principle of smooth fit, the derivative from the left and from the right at d have to coincide,
![]() $(\delta^{-1}-v(d)) \kappa = v(d) V'(d)$
. This yields
$(\delta^{-1}-v(d)) \kappa = v(d) V'(d)$
. This yields
This means the function
 \begin{equation}f(x) = \begin{cases}\dfrac{2\delta \sigma^{2} + \theta^{2}w(x)}{ w(x)^{\frac{\theta^{2}}{2\delta \sigma^{2}+\theta^{2}}}} \, \dfrac{\kappa (\theta-\eta) w(d)^{\frac{\theta^{2}}{2\delta \sigma^{2}+\theta^{2}}} }{\delta (\delta (2\delta\sigma^{2}+\theta^{2}) +\kappa (\theta-\eta)(2\delta \sigma^{2}+\theta^{2} w(d)))} & \mbox{if } x \leq d,\\ \\[-7pt] \dfrac{1}{\delta } -\dfrac{ (2\delta \sigma^{2}+\theta^{2})\textrm{e}^{-\kappa (x-d)}}{\delta(2\delta \sigma^{2}+\theta^{2}) + \kappa(\theta-\eta)(2\delta \sigma^{2}+\theta^{2}w(d))} & \mbox{if } x>d \end{cases}\end{equation}
\begin{equation}f(x) = \begin{cases}\dfrac{2\delta \sigma^{2} + \theta^{2}w(x)}{ w(x)^{\frac{\theta^{2}}{2\delta \sigma^{2}+\theta^{2}}}} \, \dfrac{\kappa (\theta-\eta) w(d)^{\frac{\theta^{2}}{2\delta \sigma^{2}+\theta^{2}}} }{\delta (\delta (2\delta\sigma^{2}+\theta^{2}) +\kappa (\theta-\eta)(2\delta \sigma^{2}+\theta^{2} w(d)))} & \mbox{if } x \leq d,\\ \\[-7pt] \dfrac{1}{\delta } -\dfrac{ (2\delta \sigma^{2}+\theta^{2})\textrm{e}^{-\kappa (x-d)}}{\delta(2\delta \sigma^{2}+\theta^{2}) + \kappa(\theta-\eta)(2\delta \sigma^{2}+\theta^{2}w(d))} & \mbox{if } x>d \end{cases}\end{equation}
is the natural candidate for the solution to the original problem.
Theorem 4.3. Suppose
![]() $\theta \leq \eta + \sqrt{2\delta \sigma^{2} +\eta^{2}}$
or
$\theta \leq \eta + \sqrt{2\delta \sigma^{2} +\eta^{2}}$
or
![]() $d\leq x_{0}$
. Then the value function v(x) is given by (4.6). The optimal strategy is
$d\leq x_{0}$
. Then the value function v(x) is given by (4.6). The optimal strategy is
![]() $\{ b^\ast (D^\ast_t)\}_t$
, with
$\{ b^\ast (D^\ast_t)\}_t$
, with
![]() $b^\ast(x)= b(x)$
for
$b^\ast(x)= b(x)$
for
![]() $x \leq d$
and
$x \leq d$
and
![]() $b^\ast(x)=1$
for
$b^\ast(x)=1$
for
![]() $x>d$
.
$x>d$
.
Proof. f(x) is the difference between two convex functions and solves the HJB equation
with optimiser
![]() $b^\ast(x)$
, where the second derivative is understood as one-sided at
$b^\ast(x)$
, where the second derivative is understood as one-sided at
![]() $x=d$
. Thus, the assertion follows as in the proofs of Theorems 2.1 and 4.1.
$x=d$
. Thus, the assertion follows as in the proofs of Theorems 2.1 and 4.1.
Remark 4.4. For
![]() $\theta \leq \eta + \sqrt{2\delta \sigma^2 + \eta^2}$
or
$\theta \leq \eta + \sqrt{2\delta \sigma^2 + \eta^2}$
or
![]() $d< x_0$
the function
$d< x_0$
the function
![]() $b^\ast(x)$
has a jump at
$b^\ast(x)$
has a jump at
![]() $x=d$
. A construction similar to the proof of [Reference Halidias and Kloeden10, Theorem 3.1] together with, e.g., [Reference Lan and Wu13, Theorems 1.1 and 1.4] shows that there exists a strong solution Y to the stochastic differential equation
$x=d$
. A construction similar to the proof of [Reference Halidias and Kloeden10, Theorem 3.1] together with, e.g., [Reference Lan and Wu13, Theorems 1.1 and 1.4] shows that there exists a strong solution Y to the stochastic differential equation
![]() $Y_t = \Delta_0 + \int_{0}^t g(Y_s) \,\textrm{d} s - \int_0^t \sigma b(Y_s) \,\textrm{d} W_s$
, where
$Y_t = \Delta_0 + \int_{0}^t g(Y_s) \,\textrm{d} s - \int_0^t \sigma b(Y_s) \,\textrm{d} W_s$
, where
 \begin{align*} g(x) = \begin{cases} \theta-\eta-\theta b(x) , &\quad x\leq d , \\[3pt] -\eta b(d) , & \quad x>d. \end{cases} \end{align*}
\begin{align*} g(x) = \begin{cases} \theta-\eta-\theta b(x) , &\quad x\leq d , \\[3pt] -\eta b(d) , & \quad x>d. \end{cases} \end{align*}
So, in order to see that the process
![]() $D^\ast$
exists, consider
$D^\ast$
exists, consider
which has the desired properties.
4.5. The case
 $\theta > \eta+\sqrt{2\delta \sigma^{2} +\eta^{2}}$
and
$\theta > \eta+\sqrt{2\delta \sigma^{2} +\eta^{2}}$
and
 $d> x_{0}$
$d> x_{0}$
In this case the optimiser b(x) is strictly increasing with
![]() $b(x_0)=1$
. Hence, we expect that above the level
$b(x_0)=1$
. Hence, we expect that above the level
![]() $x_0$
no reinsurance is taken. With V(x) given by (4.3) for
$x_0$
no reinsurance is taken. With V(x) given by (4.3) for
![]() $x \in [0,x_0]$
and
$x \in [0,x_0]$
and
![]() $V(x) = [C_1\textrm{e}^{-\kappa x} + C_2 \textrm{e}^{\check \kappa x}] V(0)$
for
$V(x) = [C_1\textrm{e}^{-\kappa x} + C_2 \textrm{e}^{\check \kappa x}] V(0)$
for
![]() $x \in [x_0,d]$
, we are looking for a smooth fit. This gives
$x \in [x_0,d]$
, we are looking for a smooth fit. This gives
 \begin{align*}C_1 \textrm{e}^{-\kappa x_0} + C_2 \textrm{e}^{\check \kappa x_0} & = \frac{2 \delta \sigma^2 +\theta^2 w(x_0)}{2 \delta \sigma^2 + \theta^2} w(x_0)^{-\theta^{2}/(2\delta\sigma^{2}+\theta^{2})} ,\\ \\[-9pt] C_2 \check \kappa \textrm{e}^{\check \kappa x_0} - C_1 \kappa \textrm{e}^{-\kappa x_0} & =\frac{\delta}{(\theta -\eta)} w(x_0)^{-\theta^{2}/(2\delta\sigma^{2}+\theta^{2})} , \end{align*}
\begin{align*}C_1 \textrm{e}^{-\kappa x_0} + C_2 \textrm{e}^{\check \kappa x_0} & = \frac{2 \delta \sigma^2 +\theta^2 w(x_0)}{2 \delta \sigma^2 + \theta^2} w(x_0)^{-\theta^{2}/(2\delta\sigma^{2}+\theta^{2})} ,\\ \\[-9pt] C_2 \check \kappa \textrm{e}^{\check \kappa x_0} - C_1 \kappa \textrm{e}^{-\kappa x_0} & =\frac{\delta}{(\theta -\eta)} w(x_0)^{-\theta^{2}/(2\delta\sigma^{2}+\theta^{2})} , \end{align*}
from which
![]() $C_1$
and
$C_1$
and
![]() $C_2$
can be obtained. Note that
$C_2$
can be obtained. Note that
![]() $C_1,C_2 > 0$
. Algebraically, the minimiser in (4.1) for
$C_1,C_2 > 0$
. Algebraically, the minimiser in (4.1) for
![]() $x > x_0$
becomes
$x > x_0$
becomes
This is an increasing function in x with value 1 in
![]() $x_0$
. This shows that V(x) indeed solves (4.1). In particular, by Theorem 4.1,
$x_0$
. This shows that V(x) indeed solves (4.1). In particular, by Theorem 4.1,
![]() $V(x) = {\mathbb{E}}^x\big[\textrm{e}^{-\delta \vartheta(b)}\big]$
with V(0) chosen such that
$V(x) = {\mathbb{E}}^x\big[\textrm{e}^{-\delta \vartheta(b)}\big]$
with V(0) chosen such that
![]() $V(d) = 1$
.
$V(d) = 1$
.
For our original problem, we again look for a smooth fit of the first derivatives at
![]() $x=d$
in order to find v(d). That is,
$x=d$
in order to find v(d). That is,
Because the drift and the volatility terms in the stochastic differential equation are continuous, it is clear that
![]() $D^*$
exists. Also in this case we get, in the same way as for
$D^*$
exists. Also in this case we get, in the same way as for
![]() $\theta \le \eta +\sqrt{2\delta \sigma^{2} +\eta^{2}}$
, the following result.
$\theta \le \eta +\sqrt{2\delta \sigma^{2} +\eta^{2}}$
, the following result.
Theorem 4.4. Suppose
![]() $\theta > \eta +\sqrt{2\delta \sigma^{2} +\eta^{2}}$
and
$\theta > \eta +\sqrt{2\delta \sigma^{2} +\eta^{2}}$
and
![]() $d > x_{0}$
. Then the function obtained above is the value function.
$d > x_{0}$
. Then the function obtained above is the value function.
5. A numerical example
We will now consider an explicit example for the function v, where we assume the position of the first insurer and optimise the discounted time spent in drawdown with respect to the retention level of proportional reinsurance. We consider
![]() $\sigma=1.4$
,
$\sigma=1.4$
,
![]() $\delta=1.0117$
,
$\delta=1.0117$
,
![]() $\eta=0.2$
, and
$\eta=0.2$
, and
![]() $d=1.5$
to be predetermined. As we have seen above, the security loading
$d=1.5$
to be predetermined. As we have seen above, the security loading
![]() $\theta$
affects whether and how much reinsurance is bought, such that it makes sense to regard the target function v and the optimal strategy b as functions of the two variables
$\theta$
affects whether and how much reinsurance is bought, such that it makes sense to regard the target function v and the optimal strategy b as functions of the two variables
![]() $\theta$
and x.
$\theta$
and x.
If we define the (strictly decreasing) function
![]() $x_{0} \,{:}\, (\sigma^{2}\check{\kappa} , \infty) \to (0,\infty)$
analogously to (4.5), we see that
$x_{0} \,{:}\, (\sigma^{2}\check{\kappa} , \infty) \to (0,\infty)$
analogously to (4.5), we see that
![]() $\theta$
fulfils the conditions of ‘cheap reinsurance’ if
$\theta$
fulfils the conditions of ‘cheap reinsurance’ if
![]() $\theta \in (\eta , x_{0}^{-1}(d)]$
, and that it can be called ‘expensive’ in the above sense if
$\theta \in (\eta , x_{0}^{-1}(d)]$
, and that it can be called ‘expensive’ in the above sense if
![]() $\theta >x_{0}^{-1}(d) $
. In the first case, reinsurance will optimally always be bought until the drawdown x is larger than d, whereas in the second case it is optimal to abstain from reinsurance when the drawdown grows close to d. If the drawdown is larger than d, it is never optimal to buy reinsurance. Thus, dealing with the functions
$\theta >x_{0}^{-1}(d) $
. In the first case, reinsurance will optimally always be bought until the drawdown x is larger than d, whereas in the second case it is optimal to abstain from reinsurance when the drawdown grows close to d. If the drawdown is larger than d, it is never optimal to buy reinsurance. Thus, dealing with the functions
![]() $v(\theta,x)$
,
$v(\theta,x)$
,
![]() $V(\theta,x)$
, and
$V(\theta,x)$
, and
![]() $b(\theta,x)$
, we need to distinguish the five areas that could contain the tuple
$b(\theta,x)$
, we need to distinguish the five areas that could contain the tuple
![]() $(\theta,x)$
. This is illustrated on the left of Figure 1. The horizontal axis represents the possible values for the initial drawdown x. The critical value d is the boundary of the area where the drawdown is perceived as unfavourable. The vertical axis represents the values
$(\theta,x)$
. This is illustrated on the left of Figure 1. The horizontal axis represents the possible values for the initial drawdown x. The critical value d is the boundary of the area where the drawdown is perceived as unfavourable. The vertical axis represents the values
![]() $\theta$
may attain and therefore starts at
$\theta$
may attain and therefore starts at
![]() $\eta$
.
$\eta$
.
![]() $\theta=x_0^{-1}(d)$
is the largest
$\theta=x_0^{-1}(d)$
is the largest
![]() $\theta$
such that the retention level
$\theta$
such that the retention level
![]() $b=1$
is never chosen if the drawdown is currently uncritical. For those
$b=1$
is never chosen if the drawdown is currently uncritical. For those
![]() $\theta$
lying above this value, the dashed curve corresponds to the function
$\theta$
lying above this value, the dashed curve corresponds to the function
![]() $x_{0}(\theta)$
and thus illustrates the boundary of the area where
$x_{0}(\theta)$
and thus illustrates the boundary of the area where
![]() $b=1$
is optimal.
$b=1$
is optimal.

Figure 1. Numerical example. Left: The different cases divide the plane into five parts. Right: The optimal strategy.
We have
![]() $\check{\kappa} \sigma^{2} = \eta+ \sqrt{2\delta\sigma^{2}+\eta^{2}} \approx 2.2015$
, and the optimiser of the HJB equation is the increasing function
$\check{\kappa} \sigma^{2} = \eta+ \sqrt{2\delta\sigma^{2}+\eta^{2}} \approx 2.2015$
, and the optimiser of the HJB equation is the increasing function
![]() $b(\theta,x)$
defined as in (4.4). The graph of this function is displayed on the right in Figure 1. The value
$b(\theta,x)$
defined as in (4.4). The graph of this function is displayed on the right in Figure 1. The value
![]() $b(\theta, x)$
depends on the current drawdown x and the safety loading of the reinsurance premium
$b(\theta, x)$
depends on the current drawdown x and the safety loading of the reinsurance premium
![]() $\theta$
. The border of the flat area at the top can be interpreted as the function
$\theta$
. The border of the flat area at the top can be interpreted as the function
![]() $x_{0}(\theta)$
.
$x_{0}(\theta)$
.
![]() $x_{0}(\theta)$
does not exist for
$x_{0}(\theta)$
does not exist for
![]() $\theta \leq 2.2015$
. With increasing
$\theta \leq 2.2015$
. With increasing
![]() $\theta\geq 2.2015$
, the function decays such that
$\theta\geq 2.2015$
, the function decays such that
![]() $x_{0}(\theta) > d =1.5$
if
$x_{0}(\theta) > d =1.5$
if
![]() $\theta$
is sufficiently close to the critical value
$\theta$
is sufficiently close to the critical value
![]() $2.2015$
. This holds true for all
$2.2015$
. This holds true for all
![]() $\theta \leq x_{0}^{-1}(d)$
, where
$\theta \leq x_{0}^{-1}(d)$
, where
![]() $x_{0}^{-1}(d) \approx 2.243$
denotes the unique solution to
$x_{0}^{-1}(d) \approx 2.243$
denotes the unique solution to
![]() $x_{0}(\theta )=d$
. For
$x_{0}(\theta )=d$
. For
![]() $x>d$
,
$x>d$
,
![]() $b(\theta,x)=1$
. Figure 2 shows plots of the functions
$b(\theta,x)=1$
. Figure 2 shows plots of the functions
![]() $V(\theta, x) \,{:}\, x \mapsto {\mathbb{E}}^{x} \big(\textrm{e}^{-\delta \vartheta^{b^{\star}}}\big)$
and
$V(\theta, x) \,{:}\, x \mapsto {\mathbb{E}}^{x} \big(\textrm{e}^{-\delta \vartheta^{b^{\star}}}\big)$
and
![]() $v(\theta,x)$
. Small values of V suggest that the controlled process starting below (above) d stays below (above) the critical level for a long time, whereas V close to 1 has the interpretation that the process will soon hit d. Because the optimal strategy for
$v(\theta,x)$
. Small values of V suggest that the controlled process starting below (above) d stays below (above) the critical level for a long time, whereas V close to 1 has the interpretation that the process will soon hit d. Because the optimal strategy for
![]() $x>d$
is independent of
$x>d$
is independent of
![]() $\theta$
, V is independent of
$\theta$
, V is independent of
![]() $\theta$
in that region as well:
$\theta$
in that region as well:
![]() $V(\theta ,x)=\exp(-\kappa (x-d))$
,
$V(\theta ,x)=\exp(-\kappa (x-d))$
,
![]() $x>d$
.
$x>d$
.

Figure 2.
![]() $V(\theta,x)$
(left) and
$V(\theta,x)$
(left) and
![]() $v(\theta,x)$
(right).
$v(\theta,x)$
(right).
6. Concluding remarks
We have solved explicitly the problem of minimising the discounted time in drawdown by proportional reinsurance for a diffusion approximation and found the reinsurance strategy. For a process with independent and stationary increments, the difference from the past maximum is an analogue of reflection at a barrier. This corresponds to paying dividends. Minimising the time in drawdown thus forces the surplus to stay in a favourable area. Because we considered monetary values that are already discounted by the riskless interest rate, the solution to our problem corresponds to similar quantities considered in the literature. It turned out that if the process is in drawdown, reinsurance is not taken in order to leave the area as quickly as possible. If the drawdown process is below the critical line, there is a trade-off between tending to zero quickly and not returning to the unfavourable area. If reinsurance is expensive, no reinsurance becomes optimal close to the drawdown area. If reinsurance is not too expensive then reinsurance is always bought. The closer the process approaches the maximum, the more cautious the insurer will behave. The optimal strategy tends to full reinsurance. Basing decisions on the minimisation of drawdowns, the insurer will not have any cause to make profits. Indeed, under the optimal strategy the running maximum of the surplus will be constant. This is of course acceptable for the regulator but will not be in the interests of the shareholders. We conclude that a criterion solely taking drawdowns into account is not reasonable.
However, to prevent drawdowns is preferable. But one also has to acknowledge the generation of future profits. One possibility is to introduce an ‘incentive to grow’. We consider this in [Reference Brinker and Schmidli5], where we also take dividend payments into account. More specifically, let
![]() $L_t$
be an adapted increasing process with
$L_t$
be an adapted increasing process with
![]() $L_{0-} =0$
denoting the accumulated dividend process. The corresponding surplus process is then
$L_{0-} =0$
denoting the accumulated dividend process. The corresponding surplus process is then
![]() $X_t^{b,L} = X_t^b - L_t$
and the corresponding drawdown process becomes
$X_t^{b,L} = X_t^b - L_t$
and the corresponding drawdown process becomes
![]() $D_t^{b,L} = \max_{s \le t} X_s^{b,L} - X_t^{b,L}$
. The goal is then to maximise
$D_t^{b,L} = \max_{s \le t} X_s^{b,L} - X_t^{b,L}$
. The goal is then to maximise
![]() ${\mathbb{E}}^{x}\bigl[ \int_0^\infty \textrm{e}^{-\delta t} \,\textrm{d} L_t - \kappa \int_0^\infty \textrm{e}^{-\delta t} \textbf{1}_{\{ D_t > d \} } \,\textrm{d}t\bigr]$
for some weight
${\mathbb{E}}^{x}\bigl[ \int_0^\infty \textrm{e}^{-\delta t} \,\textrm{d} L_t - \kappa \int_0^\infty \textrm{e}^{-\delta t} \textbf{1}_{\{ D_t > d \} } \,\textrm{d}t\bigr]$
for some weight
![]() $\kappa > 0$
. Then, a dividend on
$\kappa > 0$
. Then, a dividend on
![]() $\{D_t^{b,L} = 0\}$
may be favourable to full reinsurance. Also, further optimisation criteria are thinkable. One could, for example, add a penalising term for low surplus, as in [Reference Schmidli and Vierkötter17], minimising
$\{D_t^{b,L} = 0\}$
may be favourable to full reinsurance. Also, further optimisation criteria are thinkable. One could, for example, add a penalising term for low surplus, as in [Reference Schmidli and Vierkötter17], minimising
![]() $\int_0^\infty \textrm{e}^{-\delta t} \big[\textbf{1}_{\{ D_t > d \} } + \varphi(X_t^b)\big] \,\textrm{d} t$
for some decreasing convex function
$\int_0^\infty \textrm{e}^{-\delta t} \big[\textbf{1}_{\{ D_t > d \} } + \varphi(X_t^b)\big] \,\textrm{d} t$
for some decreasing convex function
![]() $\varphi$
. Then, an increase of the maximum
$\varphi$
. Then, an increase of the maximum
![]() $\overline{X_{t}^{b}}$
on
$\overline{X_{t}^{b}}$
on
![]() $\{D_t^{b} = 0\}$
will lower the penalising term
$\{D_t^{b} = 0\}$
will lower the penalising term
![]() $\varphi(X_t^b)$
in the future. This alternative will be more complicated to solve because we have to track both
$\varphi(X_t^b)$
in the future. This alternative will be more complicated to solve because we have to track both
![]() $X_t$
and
$X_t$
and
![]() $D_t$
. A third possibility could be to add a reward for increasing the maximum at zero; we then want to maximise
$D_t$
. A third possibility could be to add a reward for increasing the maximum at zero; we then want to maximise
![]() ${\mathbb{E}}^{x}\bigl[ \kappa \int_0^\infty \textrm{e}^{-\delta t} \,\textrm{d} \overline{X_t^b} - \int_0^\infty \textrm{e}^{-\delta t} \textbf{1}_{\{ D_t > d \} } \,\textrm{d}t\bigr]$
. This corresponds to a dividend that is only allowed to be paid when the drawdown process is at zero. We will address this problem in our future research [Reference Brinker and Schmidli6].
${\mathbb{E}}^{x}\bigl[ \kappa \int_0^\infty \textrm{e}^{-\delta t} \,\textrm{d} \overline{X_t^b} - \int_0^\infty \textrm{e}^{-\delta t} \textbf{1}_{\{ D_t > d \} } \,\textrm{d}t\bigr]$
. This corresponds to a dividend that is only allowed to be paid when the drawdown process is at zero. We will address this problem in our future research [Reference Brinker and Schmidli6].
Acknowledgements
The authors thank two unknown referees for their valuable comments on a first version of the paper.
Competing Interests
There were no competing interests to declare which arose during the preparation or publication process of this article.