No CrossRef data available.
Article contents
On a generalization of a waiting time problem and some combinatorial identities
Published online by Cambridge University Press: 30 March 2016
Abstract
In this paper we give an extension of the results of the generalized waiting time problem given by El-Desouky and Hussen (1990). An urn contains m types of balls of unequal numbers, and balls are drawn with replacement until first duplication. In the case of finite memory of order k, let ni be the number of type i, i = 1, 2, …, m. The probability of success pi = ni/N, i = 1, 2, …, m, where ni is a positive integer and 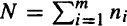 Let Ym,k be the number of drawings required until first duplication. We obtain some new expressions of the probability function, in terms of Stirling numbers, symmetric polynomials, and generalized harmonic numbers. Moreover, some special cases are investigated. Finally, some important new combinatorial identities are obtained.
Let Ym,k be the number of drawings required until first duplication. We obtain some new expressions of the probability function, in terms of Stirling numbers, symmetric polynomials, and generalized harmonic numbers. Moreover, some special cases are investigated. Finally, some important new combinatorial identities are obtained.
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 2015


