Article contents
Exact and limiting distribution of sustained maxima
Published online by Cambridge University Press: 14 July 2016
Abstract
Define a random variable
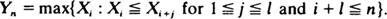
We refer to Yn as a sustained maximum. Under the assumption that the Xi's are i.i.d. the exact distribution of Yn is obtained. Under certain conditions on the underlying distribution F we obtain weak limit results for the Yn as well. Also a combinatorial extreme-value problem is solved.
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1983
Footnotes
Research supported by the National Science Foundation under Grant MCS8202259.
References
- 1
- Cited by


