Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-24T02:51:19.808Z Has data issue: false hasContentIssue false
  • English
  • Français

Conditional tail independence in Archimedean copula models

Part of: Nonparametric inference Multivariate analysis Stochastic processes

Published online by Cambridge University Press:  01 October 2019

Michael Falk ,
Simone A. Padoan  and
Florian Wisheckel Open the ORCID record for Florian Wisheckel [Opens in a new window]
Michael Falk*
Affiliation:
University of Würzburg
Simone A. Padoan*
Affiliation:
Bocconi University of Milan
Florian Wisheckel*
Affiliation:
University of Würzburg
*
* Postal address: Chair of Mathematics VIII, University of Würzburg, Emil-Fischer-Str. 30, 97074 Würzburg, Germany.
*** Postal address: Department of Decision Sciences, Bocconi University of Milan, via Roentgen, 1 20136 Milan, Italy.
* Postal address: Chair of Mathematics VIII, University of Würzburg, Emil-Fischer-Str. 30, 97074 Würzburg, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

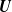Consider a random vector $\textbf{U}$ whose distribution function coincides in its upper tail with that of an Archimedean copula. We report the fact that the conditional distribution of $\textbf{U}$ , conditional on one of its components, has under a mild condition on the generator function independent upper tails, no matter what the unconditional tail behavior is. This finding is extended to Archimax copulas.

Keywords

Archimedean copulaconditional distributionasymptotic tail independencedomain of attractionextreme value distributionArchimax copulaD-norm

MSC classification

Primary: 60G70: Extreme value theory; extremal processes
Secondary: 62G32: Statistics of extreme values; tail inference 62H05: Characterization and structure theory
Type
Research Papers
Information
Journal of Applied Probability , Volume 56 , Issue 3 , September 2019 , pp. 858 - 869
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Charpentier, A., Fougères, A., Genest, C. and Nešlehová, J. (2014). Multivariate Archimax copulas. J. Multivariate Anal. 126, 118–136.CrossRefGoogle Scholar
Charpentier, A. and Segers, J. (2009). Tails of multivariate Archimedean copulas. J. Multivariate Anal. 100, 1521–1537.CrossRefGoogle Scholar
Draisma, G. et al. (2004). Bivariate tail estimation: dependence in asymptotic independence. Bernoulli 10, 251–280.CrossRefGoogle Scholar
Falk, M. (2019). Multivariate Extreme Value Theory and D-Norms. Springer, New York.CrossRefGoogle Scholar
Falk, M., Hüsler, J. and Reiss, R.-D. (2011). Laws of Small Numbers: Extremes and Rare Events, 3rd edn. Birkhäuser, Basel.CrossRefGoogle Scholar
Galambos, J. (1987). The Asymptotic Theory of Extreme Order Statistics, 2nd edn. Krieger, Malabar.Google Scholar
Guillou, A., Padoan, S. A. and Rizzelli, S. (2018). Inference for asymptotically independent samples of extremes. J. Multivariate Anal. 167, 114–135.CrossRefGoogle Scholar
Hüsler, J. and Li, D. (2009). Testing asymptotic independence in bivariate extremes. J. Statist. Planning Infer. 139, 990–998.CrossRefGoogle Scholar
McNeil, A. J. and Nešlehová, J. (2009). Multivariate archimedean copulas, d-monotone functions and $\ell_1$ -norm symmetric distributions. Ann. Statist. 37, 3059–3097.CrossRefGoogle Scholar
Nelsen, R. B. (2006). An Introduction to Copulas, 2nd edn. Springer Series in Statistics. Springer, New York.Google Scholar
Sklar, A. (1959). Fonctions de répartition à n dimensions et leurs marges. Pub. Inst. Stat. Univ. Paris 8, 229–231.Google Scholar
Sklar, A. (1996). Random variables, distribution functions, and copulas – a personal look backward and forward. In Distributions with Fixed Marginals and Related Topics, eds Rüschendorf, L., Schweizer, B., and Taylor, M. D.. Lecture Notes – Monograph Series, Vol. 28. Institute of Mathematical Statistics, Hayward, CA, pp. 1–14.Google Scholar