No CrossRef data available.
Article contents
Asymptotics of the overflow in urn models
Published online by Cambridge University Press: 11 July 2022
Abstract
Consider a finite or infinite collection of urns, each with capacity r, and balls randomly distributed among them. An overflow is the number of balls that are assigned to urns that already contain r balls. When 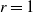 $r=1$
, this is the number of balls landing in non-empty urns, which has been studied in the past. Our aim here is to use martingale methods to study the asymptotics of the overflow in the general situation, i.e. for arbitrary r. In particular, we provide sufficient conditions for both Poissonian and normal asymptotics.
$r=1$
, this is the number of balls landing in non-empty urns, which has been studied in the past. Our aim here is to use martingale methods to study the asymptotics of the overflow in the general situation, i.e. for arbitrary r. In particular, we provide sufficient conditions for both Poissonian and normal asymptotics.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust



