Article contents
Levels of null persistency for Markov chains
Published online by Cambridge University Press: 14 July 2016
Abstract
In the study of null-persistent Markov chains the sequence 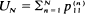 plays an important role. (See for example, Orey (1971), Athreya and Ney (1980).) In this paper we consider the rate of growth of UN to ∞ as N → ∞. This rate of growth is related to the rate of growth of
plays an important role. (See for example, Orey (1971), Athreya and Ney (1980).) In this paper we consider the rate of growth of UN to ∞ as N → ∞. This rate of growth is related to the rate of growth of 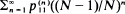 as N → ∞ and also to the rate at which
as N → ∞ and also to the rate at which 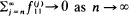 as n → ∞.
as n → ∞.
- Type
- Short Communications
- Information
- Copyright
- Copyright © Applied Probability Trust 1982
References
- 1
- Cited by


