1. Introduction
Grass-fed beef (GFB) production in the United States has experienced growth and increased research and development attention over the last two decades because of human health, environmental, animal welfare, and sustainability perspectives (Mills, Reference Mills2003; McCluskey et al., Reference McCluskey, Wahl, Li and Wandschneider2005). According to Williams (Reference Williams2013), domestically produced GFB retail sales increased from less than $5 million with only about 100 GFB producers in 1998 to $400 million in 2012. Consumer survey results have shown that 20%–30% of U.S. beef consumers are willing to pay premium prices for GFB (Cox et al., Reference Cox, Kerth, Gentry, Prevatt, Braden and Jones2006; Umberger et al., Reference Umberger, Feuz, Calkins and Killinger2002). Furthermore, the U.S. imports GFB from New Zealand and Australia (Umberger, Boxall, and Lacy, Reference Umberger, Boxall and Lacy2009; U.S. Department Agriculture, Economic Research Service [USDA-ERS], 2015), suggesting the U.S. GFB industry has significant growth potential. Existing and potential GFB producers can benefit from knowing how their operations can be structured to become more efficient and profitable. The present study evaluates productivity and profitability measures of GFB production and the variables that influence the production efficiency of U.S. GFB operations. We are unaware of previous studies that have focused on the efficiency of GFB operations.
Though demand for GFB appears to be increasing, GFB production continues to represent a small percentage of U.S. beef production. Gwin (Reference Gwin2009) estimated GFB production at 50,000–100,000 head in 2008, constituting less than 0.5% of the total U.S. beef produced. This is supported by Pelletier, Pirog, and Rasmussen (Reference Pelletier, Pirog and Rasmussen2010), who reported the share of GFB production to be less than 1% of total U.S. beef produced. Nonetheless, it has become easier for U.S. consumers to identify sources of GFB for purchase, as casual observation suggests it is now available in more grocery stores, restaurants, and farmers’ markets than 10 years ago. Supporting these casual observations, Mathews and Johnson (Reference Mathews and Johnson2013) state that alternative beef production, which includes organic, natural, and grass-fed, constitutes about 3% of the total U.S. beef market and has grown about 20% per year in recent years. The GFB segment is part of a larger U.S. beef industry that is the second-largest U.S. agricultural industry. The U.S. beef industry is the largest fed cattle industry in the world and the world's largest producer of beef (USDA-ERS, 2012).
Though limited research has addressed GFB farm efficiency, several studies have examined beef cow-calf industry production performance measures. Studies have estimated the technical, allocative, and scale efficiencies of cow-calf farms using a nonparametric linear programming-based approach known as data envelopment analysis (Featherstone, Langemeier, and Ismet, Reference Featherstone, Langemeier and Ismet1997; Rakipova, Gillespie, and Franke, Reference Rakipova, Gillespie and Franke2003). Farm size significantly affected technical efficiency (TE); herd sizes of farms up to 48 beef cows exhibited substantial economies of scale (Featherstone, Langemeier, and Ismet, Reference Featherstone, Langemeier and Ismet1997). European beef cattle farm TE and profitability have been examined using a stochastic production frontier (SPF) model, focusing on the possible impacts of the Common Agricultural Policy (Iraizoz, Bardaji, and Rapun, Reference Iraizoz, Bardaji and Rapun2005). Samarajeewa et al. (Reference Samarajeewa, Hailu, Jeffrey and Bredahl2012) determined the relative efficiency measures of cow-calf farms in Alberta, Canada. We are, however, unaware of any technical or economic efficiency studies that have analyzed GFB production in the United States.
The overall objective of this study is to determine the economic factors influencing the productivity of U.S. GFB production. The specific objectives are to determine: (1) the effects of farm specialization, farm size, and farmer demographics on the TE of U.S. GFB production; (2) the marginal productive contributions (MPCs) of inputs and outputs in U.S. GFB production; and (3) the extent of economies of scale and scope economies in U.S. GFB production. Each of these productivity measures is estimated on both whole-farm and GFB enterprise bases. Costs of production for different sizes of GFB operations are estimated, and results are compared. We estimate a stochastic input distance function (IDF) using SPF techniques.
2. Model and Methods
To estimate efficiency, a multidimensional (input and output) production technology is required. A general form for such a technology may be characterized by a stochastic IDF. The stochastic IDF approach allows us to evaluate U.S. GFB farm production technology and efficiency. In the absence of price information for inputs and outputs or when cost, profit, or revenue function estimation is impossible because of violations of required behavioral assumptions, the stochastic IDF is an appropriate method allowing for the specification of a multiple-output/multiple-input technology (Coelli and Perelman, Reference Coelli and Perelman1999). The stochastic IDF and the cost frontier are dual functions, and TE can be estimated econometrically from the stochastic IDF (Kumbhakar and Lovell, Reference Kumbhakar and Knox Lovell2000).
A reason to choose the IDF approach rather than an output distance function to represent GFB farms’ technological structure is farmers’ greater short-term control over their input than output decisions. There are a number of potential advantages of the translog IDF: (1) efficient econometric estimates of the parameters can be obtained, (2) one can formally test the hypothesis of systematic deviations from the production technology frontier, (3) the issue of potentially endogenous regressors in the distance function can be addressed using the first-order equations, (4) scope economies can be determined from the estimates, and (5) firm-specific technical inefficiency measures as a by-product of estimation can be obtained (Coelli, Hajargasht, and Knox Lovell, 2008). The reader is referred to Coelli, Hajargasht, and Knox Lovell (2008) for greater detail on this function.
A stochastic IDF is defined as the set of inputs L(Q, R) that can produce a given output vector Q with minimum input set X (Coelli et al., Reference Coelli, Prasado Rao, O'Donnell and Battese2005):
where X is defined as the input set in the Euclidean m-space ![]() ${\cal R}_ + ^m$; Q is defined as output set in the Euclidean k-space
${\cal R}_ + ^m$; Q is defined as output set in the Euclidean k-space ![]() ${\cal R}_ + ^k$; and R is defined as the farm efficiency determinants set in the Euclidean s-space
${\cal R}_ + ^k$; and R is defined as the farm efficiency determinants set in the Euclidean s-space ![]() ${\cal R}_ + ^S$.
${\cal R}_ + ^S$.
The stochastic IDF can be estimated econometrically using SPF techniques, which requires imposing homogeneity of degree one on the inputs for DI(X, Q, R). The value of the distance will be DI(X, Q, R) ⩾ 1. An IDF is nondecreasing, concave, and linearly homogeneous in inputs, and nonincreasing and quasi concave in outputs. This homogeneity condition implies that DI(δX, Q, R) = δDI(X, Q, R) for any δ > 0, and δ can be set arbitrarily at 1/Xm, resulting in DI(X, Q, R)/Xm = DI(X/Xm, Q, R) = D 1(X*, Q, R), where X* is a vector of inputs normalized by Xm.
To limit a priori restrictions on the relationships among inputs and outputs, the stochastic IDF may be approximated using a translog functional form for empirical implementation. To reveal the production technology, a translog functional form for the stochastic IDF is specified as
 $$\begin{eqnarray}
{\rm{ln}}D_i^I\left( {X,Q,R} \right) &=& {\rm{\ }}{\alpha _0} + {\rm{\ }}\mathop \sum\nolimits_m {\alpha _m}{\rm{ln}}{X_{mi}} + \frac{1}{2}\mathop \sum\nolimits_m \mathop \sum\nolimits_n {\alpha _{mn}}{\rm{ln}}{X_{mi}}{\rm{ln}}{X_{ni}}\nonumber\\
&& + {\rm{\ }}\mathop \sum\nolimits_k {\beta _k}{\rm{ln}}{Q_{ki}} + {\rm{\ }}\frac{1}{2}\mathop \sum\nolimits_k \mathop \sum\nolimits_l {\beta _{kl}}{\rm{ln}}{Q_{ki}}{\rm{ln}}{Q_{li}}\nonumber\\
&& + \mathop \sum\nolimits_k \mathop \sum\nolimits_m {\theta _{km}}{\rm{ln}}{Q_{kit}}{\rm{ln}}{X_{mi}} + \mathop \sum\nolimits_s {\varphi _s}{R_{si}} + {\rm{\ }}{\vartheta _i}.
\end{eqnarray}$$
$$\begin{eqnarray}
{\rm{ln}}D_i^I\left( {X,Q,R} \right) &=& {\rm{\ }}{\alpha _0} + {\rm{\ }}\mathop \sum\nolimits_m {\alpha _m}{\rm{ln}}{X_{mi}} + \frac{1}{2}\mathop \sum\nolimits_m \mathop \sum\nolimits_n {\alpha _{mn}}{\rm{ln}}{X_{mi}}{\rm{ln}}{X_{ni}}\nonumber\\
&& + {\rm{\ }}\mathop \sum\nolimits_k {\beta _k}{\rm{ln}}{Q_{ki}} + {\rm{\ }}\frac{1}{2}\mathop \sum\nolimits_k \mathop \sum\nolimits_l {\beta _{kl}}{\rm{ln}}{Q_{ki}}{\rm{ln}}{Q_{li}}\nonumber\\
&& + \mathop \sum\nolimits_k \mathop \sum\nolimits_m {\theta _{km}}{\rm{ln}}{Q_{kit}}{\rm{ln}}{X_{mi}} + \mathop \sum\nolimits_s {\varphi _s}{R_{si}} + {\rm{\ }}{\vartheta _i}.
\end{eqnarray}$$
Homogeneity of degree 1 in inputs implies the parametric restrictions ![]() $\mathop \sum\nolimits_m {\alpha _m} = 1$,
$\mathop \sum\nolimits_m {\alpha _m} = 1$, ![]() $\mathop \sum\nolimits_n {\alpha _{mn}} = 0$, and
$\mathop \sum\nolimits_n {\alpha _{mn}} = 0$, and ![]() $\mathop \sum\nolimits_k {\theta _{km}} = 0$. By Young's theorem, the symmetry restrictions are αmn = αnm and βkl = βlk ∀m, n, k, l.
$\mathop \sum\nolimits_k {\theta _{km}} = 0$. By Young's theorem, the symmetry restrictions are αmn = αnm and βkl = βlk ∀m, n, k, l.
To impose the homogeneity restrictions in the present study, we divided all inputs and the distance term DIi(X, Q, R) by a numeraire input, land, specified as Xm = XLAND, which is consistent with much of the literature on land-based farm production. The function is specified on a per dollar of land basis as
 $$\begin{eqnarray}
{\rm{ln}}\frac{{D_i^I\left( {X,Q,R} \right)}}{{{X_{1,i}}}} &=& {\alpha _0} + \sum\nolimits_m {{\alpha _m}{\rm{ln}}X_{mi}^{\rm{*}}} + \frac{1}{2}\sum\nolimits_m {\sum\nolimits_n {{\alpha _{mn}}{\rm{ln}}X_{mi}^{\rm{*}}{\rm{ln}}X_{ni}^{\rm{*}}} }\nonumber\\
&& + \sum\nolimits_k {{\beta _k}{\rm{ln}}{Q_{ki}}} + \frac{1}{2}\sum\nolimits_k {\sum\nolimits_l {{\beta _{kl}}{\rm{ln}}{Q_{ki}}{\rm{ln}}{Q_{li}}} }\nonumber\\
&& + \sum\nolimits_k {\sum\nolimits_m {{\theta _{km}}{\rm{ln}}{Q_{ki}}\ln X_{mi}^*} }+ \sum\nolimits_s {{\varphi _s}{R_{si}} + \ {\vartheta _i},}
\end{eqnarray}$$
$$\begin{eqnarray}
{\rm{ln}}\frac{{D_i^I\left( {X,Q,R} \right)}}{{{X_{1,i}}}} &=& {\alpha _0} + \sum\nolimits_m {{\alpha _m}{\rm{ln}}X_{mi}^{\rm{*}}} + \frac{1}{2}\sum\nolimits_m {\sum\nolimits_n {{\alpha _{mn}}{\rm{ln}}X_{mi}^{\rm{*}}{\rm{ln}}X_{ni}^{\rm{*}}} }\nonumber\\
&& + \sum\nolimits_k {{\beta _k}{\rm{ln}}{Q_{ki}}} + \frac{1}{2}\sum\nolimits_k {\sum\nolimits_l {{\beta _{kl}}{\rm{ln}}{Q_{ki}}{\rm{ln}}{Q_{li}}} }\nonumber\\
&& + \sum\nolimits_k {\sum\nolimits_m {{\theta _{km}}{\rm{ln}}{Q_{ki}}\ln X_{mi}^*} }+ \sum\nolimits_s {{\varphi _s}{R_{si}} + \ {\vartheta _i},}
\end{eqnarray}$$
which can be rewritten in general form as
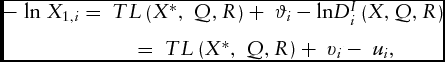 $$\begin{eqnarray}- {\rm{\ ln\ }}{X_{1,i}} & = {\rm{\ }}TL\left( {{X^{\rm{*}}},{\rm{\ }}Q,R} \right) + {\rm{\ }}{\vartheta _i} - {\rm{ln}}D_i^I\left( {X,Q,R} \right)\nonumber\\
& = {\rm{\ }}TL\left( {{X^{\rm{*}}},{\rm{\ }}Q,R} \right) + {\rm{\ }}{v_i} - {\rm{\ }}{u_i},
\end{eqnarray}$$
$$\begin{eqnarray}- {\rm{\ ln\ }}{X_{1,i}} & = {\rm{\ }}TL\left( {{X^{\rm{*}}},{\rm{\ }}Q,R} \right) + {\rm{\ }}{\vartheta _i} - {\rm{ln}}D_i^I\left( {X,Q,R} \right)\nonumber\\
& = {\rm{\ }}TL\left( {{X^{\rm{*}}},{\rm{\ }}Q,R} \right) + {\rm{\ }}{v_i} - {\rm{\ }}{u_i},
\end{eqnarray}$$
where i = 85 is the number of farms; k, l, the outputs; and m, n, the inputs. X 1 is land, specified as a normalization factor in inputs. The input variables (X*) with asterisk symbols indicate ratios of all input variable values to the quality adjusted land price. Equation 4 contains two outputs and two inputs for both whole-farm and GFB enterprise analyses. Regional dummy variables (R) are also included in this equation. The distance lnDIi(X, Q, R) from the frontier characterizes the technical inefficiency error, − ui. This random one-sided error, ui ⩾ 0, is independently distributed with truncation at zero of the N(μi, σ2u) distribution, where ![]() ${\mu _i} = \ \mathop \sum\nolimits_f {{\rm{W}}_f}\delta $, μi is defined as the conditional mean of ui, Wf is a vector of farm efficiency determinants, and δ represents unknown estimable parameters. Specifically, technical inefficiency is a function of farm- and farmer-specific characteristics. TE is derived as the expectation of − ui conditional on error term εi = vi − ui (Jondrow et al., Reference Jondrow, Knox Lovell, Materov and Schmidt1982) and is measured as TE = exp − ui.
${\mu _i} = \ \mathop \sum\nolimits_f {{\rm{W}}_f}\delta $, μi is defined as the conditional mean of ui, Wf is a vector of farm efficiency determinants, and δ represents unknown estimable parameters. Specifically, technical inefficiency is a function of farm- and farmer-specific characteristics. TE is derived as the expectation of − ui conditional on error term εi = vi − ui (Jondrow et al., Reference Jondrow, Knox Lovell, Materov and Schmidt1982) and is measured as TE = exp − ui.
Rational producers should care about economic performance measures such as MPCs of inputs and outputs in optimizing input use, returns to scale (RTS) or scale economies, and scale efficiency (SEF) in producing at the optimal farm size, and scope economies in reducing average cost by producing multiple outputs if applicable. The productivity impacts or MPCs of outputs or inputs can be estimated from the stochastic IDF model by the first-order elasticities. Using the first-order elasticities from the stochastic IDF, output and input MPCs can be estimated, respectively, as
MPCk indicates the increase in overall input use when output expands (and so is expected to be positive, like a marginal cost or output elasticity measure), and MPCm indicates the shadow value (Färe and Primont, Reference Färe and Primont1995) of the mth input relative to X 1 (and so is expected to be negative, like the slope of an isoquant).
Scale economies or RTS are calculated as the combined contribution of the K outputs Qk, or the scale elasticity (SE):
That is, the sum of the input elasticities, ![]() $\mathop \sum\nolimits_k \partial ln{X_1}/\partial ln{Q_k}$, indicates the overall input–output relationship and thus RTS. The extent of scale economies is thus implied by the shortfall of scale economies from 1; if scale economies <1, inputs do not increase proportionately with output levels, implying increasing RTS. A measure of scope economies was estimated from the stochastic IDF by taking the second cross partial output derivatives, ∂2lnDI(X, Q, R)/∂lnQk∂lnQl > 0. The scope economy measure ranges between 0 and 1, indicating no scope economy if it is equal to 0.
$\mathop \sum\nolimits_k \partial ln{X_1}/\partial ln{Q_k}$, indicates the overall input–output relationship and thus RTS. The extent of scale economies is thus implied by the shortfall of scale economies from 1; if scale economies <1, inputs do not increase proportionately with output levels, implying increasing RTS. A measure of scope economies was estimated from the stochastic IDF by taking the second cross partial output derivatives, ∂2lnDI(X, Q, R)/∂lnQk∂lnQl > 0. The scope economy measure ranges between 0 and 1, indicating no scope economy if it is equal to 0.
SEF is the potential productivity gain from moving to the optimal farm size and can be estimated from the stochastic IDF. The method for estimating SEF was introduced by Ray (Reference Ray1998, Reference Ray2003) and Balk (Reference Balk2001) for single-output multiple-input and multiple-output multiple-input distance functions. Following Ray (Reference Ray2003), the SEF for U.S. GFB production can be estimated from the stochastic IDF as
The SEF measure ranges between 0 and 1, indicating SEF exists if the SEF measure is equal to 1.
We used Stata's nonlinear combinations of estimators (or nlcom) command to estimate the statistical significance of MPCs for inputs and outputs, scale economies, RTS, elasticities, and SEF measures for the GFB production because the stochastic IDF is not a linear function. This estimation is based on the delta method.
2.1. Data
During August–September 2013, a mail survey of 1,050 U.S. GFB producers was conducted to determine their use of production and marketing practices, farm operation characteristics, management practices, criteria for selecting animals for grass finishing, pasture and grazing management for the GFB operation, producer goals and reasons for selecting the GFB enterprise, perceptions of challenges facing the GFB industry, preferences for breeding stock, general financial information, and producer demographics. The mailing list of U.S. GFB producers was created by searching the Internet for addresses of GFB producers, specifically visiting the American Grass-Fed Association (www.americangrassfed.org/) and MarketMaker (https://foodmarketmaker.com/) websites, Eatwild.com, and other sites that were identified where GFB producers advertised their products. All GFB producers for which a mailing address could be obtained were included. The questionnaire, a signed letter, and business-reply envelope were sent to producers on August 4, 2013, followed by a postcard reminder 1 week later. On August 28, 2013, a second questionnaire, signed letter, and business-reply envelope were sent to nonresponders, followed by a postcard reminder 1 week later. The Dillman, Smith, and Christian (Reference Dillman, Smith and Christian2009) tailored design method was followed in preparing the survey. Of the 1,050 surveys sent throughout the United States, 384 responses were collected for an adjusted response rate of 41%, considering bad addresses and producers no longer in the GFB business.
The last question in the survey asked GFB producers about their willingness to fill out a follow-up survey on cost and returns of GFB production in 2012. A total of 257 GFB producers agreed to complete the follow-up survey questionnaire. The follow-up questionnaire was designed in a similar manner to USDA's Agriculture Resource Management Survey questions on costs and returns. Detailed information on income and expenses was collected using this survey. Because respondents had already received up to four mailings on the first survey, we sent only two mailings of the follow-up questionnaire 2 weeks apart, both with personally addressed, signed letters and business-reply envelopes. For the follow-up survey questionnaire, a total of 85 completed responses were received from producers in 34 states (see Table 1, which lists the states by region). After adjusting for undeliverable surveys, producers who did not produce GFB, and incomplete surveys, the effective return rate was 33%.
Table 1. Summary Statistics and Variable Definitions for U.S. Grass-Fed Beef (GFB) Producers
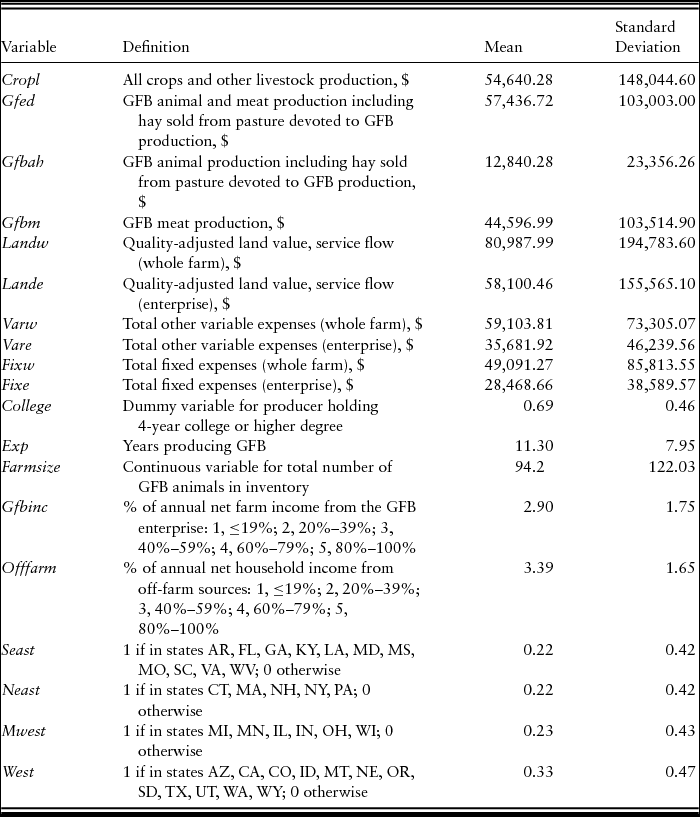
Using the costs and returns data (Table 1), we developed two outputs for both the GFB whole-farm and enterprise IDF analyses. For the whole-farm analysis, Gfed is the revenue from GFB meat and animal sales, plus revenue from hay sold from pasture devoted to GFB production. Cropl is revenue from all crops and other livestock (non-GFB) sales. For the enterprise analysis, Gfbah is revenue from GFB animal production plus revenue from hay sold from pasture devoted to GFB production. Gfbm is revenue from GFB meat sales.Footnote 1 Inputs for both analyses include: Land is quality-adjusted land price;Footnote 2 Var is total variable expenses;Footnote 3 and Fix is total fixed expenses and hired labor expenses.Footnote 4 Much of the previous research has used monetary values rather than quantities for output and input variables and aggregated all livestock outputs as one output (Morrison Paul and Nehring, Reference Morrison Paul and Nehring2005; Qushim et al., Reference Qushim, Gillespie, Paudel and Mcmillin2016). These studies have been national in scope. We followed these studies and used monetary values for our input and output variables.
In Table 1, the letters “e” or “w” at the end of each input variable indicate the value for the GFB enterprise or for the whole farm, respectively. For most of the expenses, we requested that the respondent provide the total farm expense and an estimate of the expense that was allocated to the GFB enterprise. We did not, however, request enterprise-specific expenses for the following inputs in the survey questionnaire: Repairs on Equipment; Insurance; Taxes; Vehicle/Licensing Fees; Depreciation; Custom Work; Cash Value of Feed, Farm Commodities, Fuel, Housing, Meals, Other Food, Utilities, and Vehicle for Personal Use; and Farm Management Services. In order to obtain enterprise-specific expenses for these input variables for the enterprise analysis, the percentage or portion of the GFB enterprise total return was calculated as the total GFB enterprise return (GFBER) divided by the total whole farm return (WFR) to result in GFBER/WFR. For the GFB enterprise-specific expenses for these inputs, the whole-farm expense values were multiplied by GFBER/WFR. For the whole-farm analysis, total farm returns and expenses were used.
Missing information is a common issue for survey data and may result in biased estimates and reduce regression estimate efficiency (Rubin, Reference Rubin1987). Various methods exist to handle missing data issues. The multiple imputation method (Rubin, Reference Rubin1987; Schafer, Reference Schafer1997), specifically the truncated regression imputation method, was used to estimate missing values of continuous variables in this study. We imputed eight values for missing depreciation expenses and six values for missing cash value of noncash payment for farmwork expenses incorporating farm characteristics and demographics from the earlier GFB survey. Neast, Mwest, and West are regional dummy variables for the northeastern, midwestern, and western U.S. GFB production regions, respectively (Seast is the base southeastern GFB production region). States included in each region are shown in Table 1. We grouped U.S. states into the regions based on U.S. farm resource regions as designated by USDA-ERS and similarity of states in terms of forage type, land, and weather conditions.
Having zero-value observations in estimation of the translog function may prove problematic, resulting in biased estimators of parameters of the chosen function (Battese, Reference Battese1997). A few observations in the Cropl and Gfbah variables may have zero values in our sample in cases where farms did not produce crops or sell animals, respectively. We caution readers that not all observations have zero values in these variables. Note that having a few zero-value observations may affect results of parameter estimates. Therefore, we used the Battese (Reference Battese1997) approach to deal with zero-value observations:
 $$\begin{eqnarray*}
&&\mathop \sum\nolimits_{k = 1} Q_{k,i}^d = 1{\rm{if\ }}\mathop \sum\nolimits_{k = 1} {Q_{k,i}} = 0,{\rm{\ }}\mathop \sum\nolimits_{k = 1} Q_{k,i}^d = 0{\rm{\ if\ }}\mathop \sum\nolimits_{k = 1} {Q_{k,i}}{\rm{\ }} > 0,\\
&&\quad{\rm{\ and}}\mathop \sum\nolimits_{k = 1} Q_{k,i}^{\rm{*}} = \max \left( {{Q_{k,i}},{\rm{\ }}Q_{k,i}^d} \right),
\end{eqnarray*}$$
$$\begin{eqnarray*}
&&\mathop \sum\nolimits_{k = 1} Q_{k,i}^d = 1{\rm{if\ }}\mathop \sum\nolimits_{k = 1} {Q_{k,i}} = 0,{\rm{\ }}\mathop \sum\nolimits_{k = 1} Q_{k,i}^d = 0{\rm{\ if\ }}\mathop \sum\nolimits_{k = 1} {Q_{k,i}}{\rm{\ }} > 0,\\
&&\quad{\rm{\ and}}\mathop \sum\nolimits_{k = 1} Q_{k,i}^{\rm{*}} = \max \left( {{Q_{k,i}},{\rm{\ }}Q_{k,i}^d} \right),
\end{eqnarray*}$$
where i denotes the number of observations, k = 1 is QCropl (for the whole-farm analysis) or QGfbah (for the enterprise analysis), and Qd k, i is a dummy variable accounting for the intercept change.
We also include farm-specific TE variables (W) from the GFB production survey data. The following GFB production technical inefficiency effects model was estimated as a function of farm and producer characteristics for both whole-farm and enterprise analyses:
where μi is defined as the conditional mean of ui, εi is unobservable independently distributed random variables, and the farm-specific Wf variables are defined in Table 1.
College is a producer education dummy variable indicating whether the respondent held a bachelor's degree or higher. Producers with higher educational attainment have generally been more technically efficient (Morrison Paul et al., Reference Morrison Paul, Nehring, Banker and Somwaru2004; Rakipova, Gillespie, and Franke, Reference Rakipova, Gillespie and Franke2003). Exp is a continuous variable indicating the number of years the producer had raised GFB. Producers with more farming experience are likely to have more knowledge of farming practices; experience has generally positively affected TE (Bhatt and Bhat, Reference Bhatt and Bhat2014).
Farmsize is continuous variable for operation size in terms of animals in inventory. Farms have generally been more technically efficient with increasing size (Featherstone, Langemeier, and Ismet, Reference Featherstone, Langemeier and Ismet1997; Morrison Paul et al., Reference Morrison Paul, Nehring, Banker and Somwaru2004; Samarajeewa et al., Reference Samarajeewa, Hailu, Jeffrey and Bredahl2012). Gfbinc is the percentage of annual net farm income from the GFB enterprise, categorized into five levels in 20% intervals, a measure of farm specialization. A positive impact of degree of specialization on TE would be expected if specialization improves the producer's ability to manage the operation. Previous studies have shown mixed results on the impact of specialization on TE of livestock farms. Featherstone, Langemeier, and Ismet (Reference Featherstone, Langemeier and Ismet1997) found that specialization decreased the TE of Kansas cow-calf farms, whereas Qushim et al. (Reference Qushim, Gillespie, Paudel and Mcmillin2016) found that specialization increased the TE of U.S. meat goat farms. Offfarm is the percentage of annual net household income from off-farm sources, included using five levels in 20% intervals. Producers holding off-farm employment likely devote less attention to their farming operations, potentially resulting in lower output. Alternatively, off-farm income can be invested into the farm (Qushim et al., Reference Qushim, Gillespie, Paudel and Mcmillin2016).
The single-step maximum likelihood method (Battese and Coelli, Reference Battese and Coelli1995) was used to estimate equation (4) as an error components model. Specifically, the parameters of the stochastic IDF and the technical inefficiency models are estimated jointly using SPF techniques. There are biased estimation concerns associated with two-step methods (Schmidt, Reference Schmidt2011). Accordingly, with least squares regression, if exogenous variables Wi are omitted in the first step of a two-step estimation in which Wi affects Qi and Xi and Wi are correlated, then β will be biased. The first step results using two-step methods are biased if Xi and Wi are correlated and Monte Carlo (MC) simulations show that the bias can be severe (Schmidt, Reference Schmidt2011).
3. Results
As previously discussed, data for this study were from both a first survey questionnaire including farm and farmer characteristics and a follow-up questionnaire for costs and returns. Therefore, our costs and returns data are a subsample of the first survey data. For that reason, there was concern as to whether there were differences between the first survey and the follow-up survey sample means. To compare the means of several variables in the first survey and those in the follow-up survey, we conducted t-tests to determine whether there were statistically significant differences in means of the following variables between the surveys: number of GFB cattle, total acres of GFB cattle, total farm acres, and years farming (Table 2), together providing information on whether farm size or farmer experience differed by survey. Results of the t-tests fail to reject the null hypothesis, concluding that there is not sufficient evidence to suggest the first survey and the follow-up survey sample means differ at P ⩽ 0.10 levels, suggesting that they came from similar GFB farms.
Table 2. The t-Test Results for the First and Follow-up Survey Variable Means

3.1. Comparing Costs and Returns of U.S. GFB Farms by Operation Size
To initially examine GFB production economics, the sample was divided into two operation sizes, small farms with <15 GFB slaughter-weight animals produced in 2012 and large farms with ≥15 GFB slaughter-weight animals produced. There were 47 and 38 observations for small and large farms, respectively. Note that there is a difference between the total number of GFB animals in inventory and produced GFB slaughter-weight animals. GFB producers may not keep all animals to slaughter weight, and more than 1 year may be required to raise a GFB animal to slaughter weight. A comparison of U.S. GFB enterprise expenses (in dollar value) per slaughter-weight animal is shown in Table 3. GFB enterprise variable, fixed, and total specified expenses per slaughter-weight animal for large farms were lower than for small farms. GFB enterprise returns above total specified expenses per slaughter-weight animal for large farms were higher than for small farms but were negative. This underscores the value of estimating a multioutput stochastic IDF for these farms to obtain a better estimate of the impact of farm size on productivity.
Table 3. U.S. Grass-Fed Beef (GFB) Enterprise Returns and Costs Comparison by Slaughter-Weight Animals
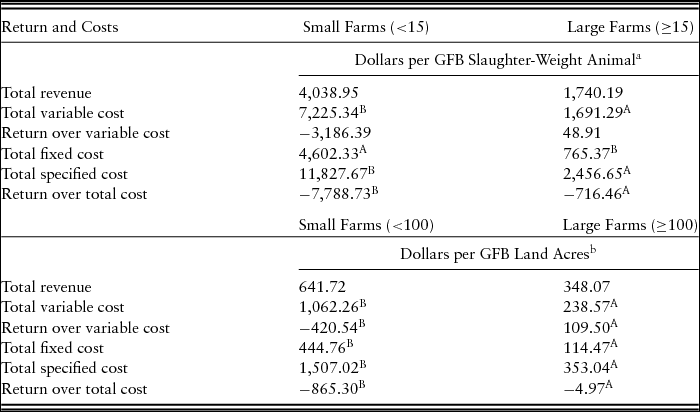
a Letters (A, B) indicate significant differences (P < 0.10) in means across columns: A = small farms with <15 GFB animals that were raised to slaughter weight on the farm in 2012; B = large farms with ≥15 GFB animals that were raised to slaughter weight on the farm in 2012.
b Letters (A, B) indicate significant differences (P < 0.10) in means across columns: A = small farms with <100 acres that were exclusively devoted to the GFB operation in 2012; B = large farms with ≥100 acres that were exclusively devoted to the GFB operation in 2012.
Note: The year 2012 was a year of severe drought in much of the United States, which would likely have affected costs and returns for GFB for some producers.
A comparison of U.S. GFB enterprise expenses per production acre exclusively devoted to the GFB operation (small and large farms) is also shown in Table 3. Small farms were defined as those with <100 acres exclusively devoted to the GFB enterprise. Large farms had ≥100 acres exclusively devoted to the GFB enterprise. Results show that GFB enterprise total, variable, and fixed expenses per acre for large farms were lower than for small farms. GFB enterprise return over variable expenses per acre for large farms was higher than for small farms. GFB enterprise return above total specified expenses per acre for large farms was higher than for small farms; however, this does not suggest that all large farm returns covered total expenses. Note, however, that 2012 was a year of severe drought in much of the United States (MacLachlan et al., Reference MacLachlan, Ramos, Hungerford and Edwards2018), so these conditions would have affected net returns for some producers. Small GFB farms, on average, used 3.3 acres per GFB animal compared with large farms with 8.4 acres per GFB animal. Thus, although returns and expenses per acre values provide some insights, intensity of land use differed, complicating the simple comparison by farm size and providing further support for the quality adjustment to land as used in our IDF analyses.
3.2. Estimating the Stochastic Input Distance Function
The likelihood ratio test, ![]() ${\cal L}{\cal R} = ( { - 2\ln [ {\frac{{{\cal L}( {{{\rm{H}}_0}} )}}{{{\cal L}( {{{\rm{H}}_{\rm{A}}}} )}}} ]} )$, was used to test the restrictions on the parameters of the stochastic IDF model, where
${\cal L}{\cal R} = ( { - 2\ln [ {\frac{{{\cal L}( {{{\rm{H}}_0}} )}}{{{\cal L}( {{{\rm{H}}_{\rm{A}}}} )}}} ]} )$, was used to test the restrictions on the parameters of the stochastic IDF model, where ![]() $\ln [ {{\cal L}( {{{\rm{H}}_0}} )} ]$ and
$\ln [ {{\cal L}( {{{\rm{H}}_0}} )} ]$ and ![]() $\ln [ {{\cal L}( {{{\rm{H}}_{\rm{A}}}} )} ]$ are values of the likelihood function under null and alternative hypotheses, respectively. The likelihood ratio test has a chi-square (χ2) distribution with the degrees of freedom given by the number of restrictions imposed in the translog model. Results of the test statistics for both U.S. GFB whole-farm and enterprise analyses are presented in Table 4.
$\ln [ {{\cal L}( {{{\rm{H}}_{\rm{A}}}} )} ]$ are values of the likelihood function under null and alternative hypotheses, respectively. The likelihood ratio test has a chi-square (χ2) distribution with the degrees of freedom given by the number of restrictions imposed in the translog model. Results of the test statistics for both U.S. GFB whole-farm and enterprise analyses are presented in Table 4.
Table 4. The Likelihood Ratio (LR) Test Results for the U.S. Grass-Fed Beef Production Model
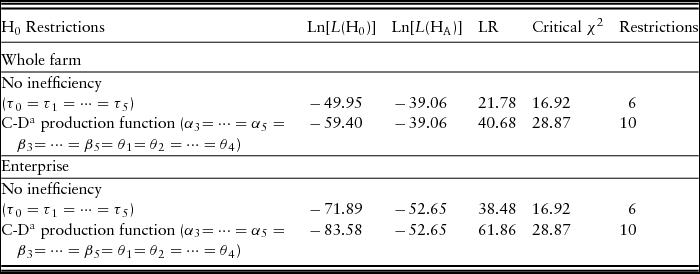
a C-D is Cobb-Douglas production function.
Note: The test results at 5% level of significance.
First, we tested whether the explanatory variables in the inefficiency model significantly explained the technical inefficiency effects. Test results show that these effects are statistically explained by the variables in the inefficiency models (Table 4). We also tested whether the translog functional form better described the underlying production technology of U.S. GFB farms relative to the alternative Cobb-Douglas functional form. Results show that the translog models are the more appropriate functional forms for the models.
The maximum likelihood parameter estimatesFootnote 5 for the stochastic IDF whole-farm and enterprise analyses are presented in Table 5. According to the estimated parameters, the stochastic IDF is found at the approximation point to be nondecreasing in inputs and nonincreasing in outputs. Moreover, the Hessian matrix of the first- and second-order partial derivatives with respect to inputs is found to be negative definite, and the corresponding Hessian matrix with respect to outputs to be positive definite. These indicate, respectively, the concavity and convexity of the underlying IDF with respect to inputs and outputs. The coefficient estimates for the output variable parameters in both analyses are significant and have expected signs. The statistically significant Cropl, Gfed, Gfbah, and Gfbm outputs suggest that increases in these outputs increase the productive contributions on both whole-farm and enterprise bases. In both the whole-farm and enterprise analyses, the second-order condition of cross effects of output, εX, QkQl > 0, are positive and significant suggesting complimentary effects between the outputs. The second-order condition of cross effects of the inputs, εX, XmXl < 0, indicate complementary effects between the inputs.
Table 5. The Input Distance Function (IDF) Estimates for U.S. Grass-Fed Beef Whole Farm and Enterprise
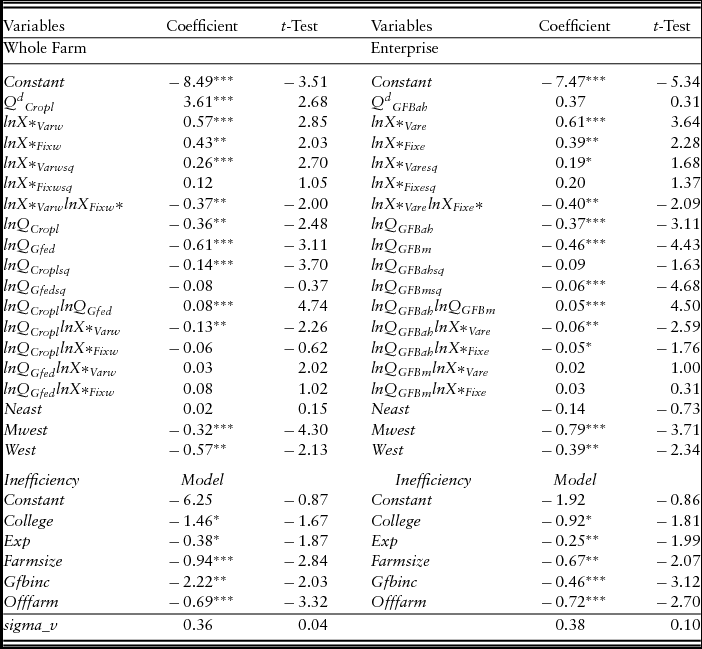
Notes: Asterisks (*, **, ***) indicate 10% level of significance, 5% level of significance, and 1% level of significance, respectively. The standard errors for the IDF estimates are estimated using robust standard errors or the Huber-White estimator.
The estimates for inefficiency model parameters for both whole-farm and enterprise models are also presented in Table 5. College education, experience, farm size, farm specialization or percentage of annual net farm income from the GFB operation, and percentage of annual net household income from off-farm sources were efficiency drivers in both models. As expected, GFB producers with college degrees were more technically efficient than producers without college degrees. Greater experience with raising GFB led to more technically efficient GFB farms. Larger farms were more technically efficient than smaller farms.
Statistical significance of GFB production specialization provides no initial evidence of economies of scope in GFB whole-farm production; farms that were more specialized were more efficient than farms that were more diversified. In both whole-farm and enterprise models, GFB producers having greater percentages of income from off-farm sources were more technically efficient than producers with lower percentages of income from off-farm sources. This suggests that having off-farm employment causes producers to more efficiently utilize their inputs (including labor) in producing GFB.
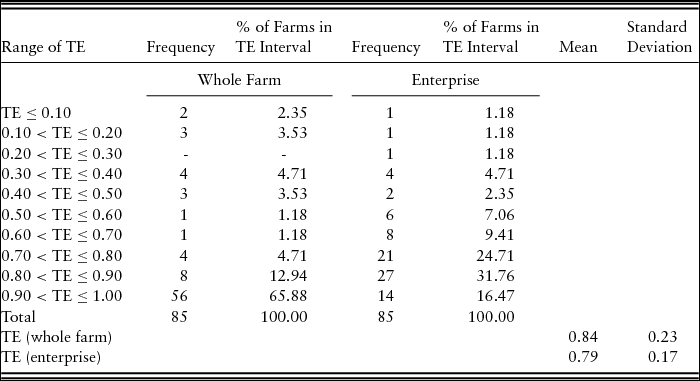
The distributions of the estimated input-oriented TE scores for both whole-farm and enterprise models are presented in Table 6. We find average TE scores of 0.84 and 0.79, respectively, for GFB farms on whole-farm and enterprise bases. This implies that the average U.S. GFB farm could reduce inputs by 16% (whole-farm basis) and 21% (GFB enterprise basis) to produce the same output as an efficient operation on the production frontier. The table also shows that more than 78% and 48% of the producers achieved TE levels of 80% or higher using whole-farm and enterprise measures, respectively. Featherstone, Langemeier, and Ismet (Reference Featherstone, Langemeier and Ismet1997) and Rakipova, Gillespie, and Franke (Reference Rakipova, Gillespie and Franke2003) found average TEs of 0.78 and 0.92 for Kansas and Louisiana beef cattle producers, respectively. Relatively low TE levels would be expected for the GFB industry given the relative newness of GFB production to many U.S. farms and limited research to provide recommendations for productive GFB production. To compare the distribution of TE differences between large and small farms, we conducted a nonparametric Kruskal-Wallis test. We defined large farms as operation sizes ≥50 GFB animals in inventory, and otherwise small farms. The test results indicate the statistical significance of the Kruskal-Wallis test at P ≤ 0.05.
Table 6. Technical Efficiency (TE) Distributions
Estimated parameters of MPCs for both whole-farm and enterprise models have theoretically correct signs, negative for inputs and positive for outputs (Table 7). MPCs for output indicate an increase in overall input use when output expands. For inputs, MPCs indicate the shadow values of inputs relative to land. All of the MPC measures in both whole-farm and enterprise analyses are statistically significant. The largest MPC in absolute value for inputs is land expense, followed by total variable expenses and total fixed expenses. The MPC for GFB production output in the whole-farm model has the largest output share—about 54% on average. The MPC for GFB meat production output in the enterprise model has the largest output share—nearly 59% on average.
Table 7. Marginal Productive Contributions (MPCs) for Inputs and Outputs, Returns to Scale, Scope Economies, and Scale Efficiency

Notes: Asterisks (*, **, ***) indicate 10% level of significance, 5% level of significance, and 1% level of significance, respectively.
GFB production overall economic performance indicators for both whole-farm and enterprise analyses are presented in Table 7. The estimated RTS parameters for U.S. GFB whole-farm and enterprise analyses show that a 1% increase in all outputs increased overall input use by 0.88% and 0.86%, respectively. These results imply an increasing RTS economy for U.S. GFB production. A measure of scope economies was estimated from the IDF by taking the second cross partial output derivatives, and it was statistically significant only for the enterprise analysis. The scope economies parameter suggests that the joint production of both GFB animal and GFB meat outputs decreased average total cost by 11% relative to the separate production of these two outputs on U.S. GFB farms.
As an economic performance measure, SEF represents the improvement in average productivity of U.S. GFB farms through a change in the scale of GFB production. The SEF measures estimated from the IDF are presented in Table 7. We used the stochastic IDF parameter estimates to determine SEF for GFB production using equation (8). Different sizes of GFB farm operations as well as the median size of GFB farms were entered into the SEF equation (8) to achieve the SEF measure of 1. The median size of the farms is 50 animals in our sample. Results of SEF measures from both whole-farm and enterprise analyses indicate that, on average, GFB farms are scale efficient if the farm's scale of production is greater than 100 animals in inventory. The SEF measure indicated that GFB farms are not scale efficient based on the median farm size, which is 50 animals.
4. Summary and Conclusions
Because the U.S. GFB industry has only recently experienced increased interest after many decades of little interest from U.S. producers and consumers, the relatively few producers who have become recently involved in the industry have had little access to information on the most efficient practices for GFB production. To reveal insights on productivity drivers in this growing segment of the beef industry, we estimated efficiency measurements including TE, scale and scope economies, and SEF for U.S. GFB production using costs and returns data. Given that our sample size is relatively small with approximately two farms per state, we suggest that results should be interpreted with caution. As such, these economic efficiency measures are conclusions of our survey sample analysis rather than the entire U.S. GFB industry. However, given that our survey sample is likely representative of the commercial U.S. GFB producers who advertised their products via the Internet (which are likely a sizable portion of the GFB producer population), our results hold some significant implications.
The effect of operation size on the efficiency and productivity of U.S. GFB enterprises is significant. A look at farm costs and returns generally showed lower costs per unit of input on both per slaughter animal produced and per acre bases for large farms. The large farms had positive cash returns (returns over variable cost) even during a drought year. The 2012 drought affected feed availability, animal mortality rates, production costs, and income for livestock producers (MacLachlan et al., Reference MacLachlan, Ramos, Hungerford and Edwards2018). However, results of simple GFB enterprise costs and returns analyses by farm size present some problems, as there are significant differences in output mix within the GFB enterprise, with some producers concentrating more heavily on animal sales (generally larger farms) and others concentrating more heavily on meat sales (generally smaller farms). Furthermore, land quality varies significantly, so simple per acre of land estimates must be interpreted with caution. These issues provide some justification for the use of multiple-input, multiple-output distance functions where output and input mixes are considered and land quality adjustments are made. Using the IDF analysis, larger GFB operations were determined to be more technically efficient than smaller operations. The IDF estimates indicate that there are significant economies of size in U.S. GFB production. Increasing RTS suggests that by expanding their operations, producers can use less input per unit produced. Results suggest that U.S. GFB farms can be scale efficient if they have greater than approximately 100 GFB animals in inventory. The average GFB farm in our sample had 100 animals in inventory, suggesting there is significant potential for increased SEF in this industry. It is noted, however, that a farm with 100 GFB animals is relatively large scale by U.S. farm standards. From our survey, the average 100-animal operation farmed 667 acres of land, as compared with the average U.S. farm of 433 acres (USDA, National Agricultural Statistics Service, 2012).
Scope economies were found through vertically integrating within the GFB supply chain. Producers who sold GFB meat and GFB animals reduced their long-run average costs of production. On a whole-farm basis, however (considering non-GFB enterprises), scope economies were not found. In addition to the scope economies estimate being nonsignificant for the whole-farm model, having higher percentages of farm returns from GFB (greater specialization in GFB) increased farm efficiency. Thus, we find no evidence to suggest that economies of scope are present in producing GFB along with other agricultural commodities.
Another way to diversify farm household income is via off-farm income. Greater off-farm income increased TE, perhaps because of the investment of off-farm income on GFB operations. Income from off-farm sources provides capital for producers to adopt new technologies and perhaps purchase more productive inputs for their operations, which in turn can lead to increased TE. Furthermore, because of time constraints, the operator labor input must be utilized more efficiently for an operator with off-farm employment to produce the same output as the full-time producer. Note that mixed results have been found in previous studies examining the impact of off-farm income on TE.
The inefficiency model estimates also reveal some additional insights. Not surprisingly, both more highly educated producers and those with more GFB farming experience operated more technically efficient farms. Considering (1) the wide range of options available to GFB producers in terms of production system (continuous or rotational grazing, etc.), breed types, and forage types; (2) the different production conditions (climate, weather, soil, etc.) under which GFB is produced; and (3) the limited research available to provide insights into the best GFB production practices, production experience would be expected to be quite important for increasing productivity in this industry.
If current trends of increased supply and demand for GFB continue for the foreseeable future, we expect more questions from current and potential GFB producers on recommended farm structure and optimal production practices. Given the many different forage species and production conditions across the United States, more targeted regional analysis would be helpful. In areas where there is particularly heightened interest in GFB, this introduces the need for research and extension efforts in this area. Although the current study provides insight into some general GFB farm structural issues such as farm size, diversification, and so forth, more specific production system questions will need to be addressed through field trials and economic analyses along the lines of those conducted by Bhandari et al. (Reference Bhandari, Gillespie, Scaglia, Wang and Salassi2015) for GFB. Coupled with the results of studies such as the present one, such studies can provide producers with guidance on how to structure their operations in a way such that profit potential is strengthened.









