1. Introduction
The environment for policy decision making has changed in recent years, with civil society calling for more openness in the policy-making process. This was clearly visible in the negotiations between the United States and the European Union (EU) over the Transatlantic Trade and Investment Partnership (TTIP) (Loon, Reference Loon2018). In addition, policy making has been affected by the issue of misinformation, which has received enormous attention in the scientific community, partly because of the U.S. presidential election in 2016. Search results with the term “fake news” increased on Google Scholar from 637 in 2015 to 12,500 in 2018.Footnote 1 These two issues challenge the way political decision making is commonly modeled.
Traditionally, trade negotiations and other international negotiations between states have not been publically transparent while being conducted. Those with access to negotiators were aware of drafts and position papers as a part of the consultation process, but such access became more limited as the negotiations reached the final phases. Negotiators preferred to unveil the results of negotiations only after completion. Then the public was allowed, through their country’s political process, to consider and accept or reject the negotiation results presented to them. The negotiations between the EU and the United States over the TTIP may be viewed as a first major departure from this nontransparent negotiation model. The EU seemed to maintain this position in the Brexit negotiations between the EU and the United Kingdom. By declaring “openness,” the EU seemed to be treating transparency as a political asset. Transparency became a major issue in the negotiations, but the social welfare effects of more transparency are not yet fully understood.
A common assertion in favor of increased public transparency in trade negotiations is that more public information leads to better social decisions and, hence, higher social welfare. However, the validity of this assertion relies on two basic assumptions: (1) the cost of processing information does not significantly increase with the amount of information processed, and (2) people can be influenced to make poor judgements about complex issues only at (very) high costs. We will argue that if either assumption is violated, increased transparency of international negotiations can reduce social welfare. The U.S. 2016 presidential campaign and election, and the UK’s 2016 Brexit process stand out as prominent examples of violations of assumption (2). “Fake news” has become the en vogue term for the conscious production and public release of misleading or false information. Indeed, there are empirically verifiable indications that some fraction of UK voters could not systematically distinguish between accurate and inaccurate public political claims. For example, Google (2016) released statistics showing that “What does it mean to leave the EU?” and “What is the EU?” were the UK’s top two Internet search engine queries in the hours immediately preceding voting on the Brexit referendum.
The economic literature on the topic of transparency of (trade) negotiations is sparse in general, and the issue of whether public transparency can ever have harmful effects is sparse in particular. The issue of transparency is closely related to the mode and exchange of information between political agents and their constituencies. Lack of transparency enables political agents to communicate misleading or false information to citizens. The objective of this article is therefore to help fill this gap by examining the social welfare effects of more public transparency in trade negotiations in the presence of costly information processing and the ability of agents to generate and release misleading or false information.
2. Transparency and misinformation in the context of the Transatlantic Trade and Investment Partnership
In this section, we first show that increased transparency can lead to higher costs of information. Second, we show how scientific information from official EU bodies was used to mislead EU citizens and to align their preferences with a private lobbying group.
2.1. Transparency
The negotiations between the EU and United States over the TTIP started in June 2013, but the European Council’s detailed directives for the negotiations (“mandate”) were not made public. Increased pressure from the European Parliament and the EU Ombudsman (2015) led to a deal that allowed Parliament access to the negotiation texts under very strict conditions.
The European Commission (2013) argued that secrecy was inevitable as a matter of international relations, emphasizing the importance of secrecy as a prerequisite for trust among the negotiators. More importantly in the context of our analysis, the European Commission (2015) argued that increased openness would reduce social welfare by inefficient use of public resources.
The European Commission responded to the wave of criticism by civil society organizations against TTIP by releasing a long list of documents that it had previously kept secret. However, the most important TTIP documents remained unavailable, and many claims, both favorable and unfavorable toward TTIP, could not be substantiated. Increased openness in the EU about TTIP negotiations inspired various U.S. groups voicing similar concerns. More than 75 U.S. trade unions, political activist groups, and academics sent a letter to U.S. trade representative Michael Froman, requesting more openness in the TTIP negotiations, asking for the same level of transparency in the United States as in the EU (AFL-CIO, 2015).
2.2. Misinformation: an example from the European Union pathogen reduction treatments debate
The use of chlorine dioxide and other pathogen reduction treatments to remove surface contamination from poultry in U.S. slaughterhouses was one of the most prominent symbols of the European anti-TTIP movement used to convince European citizens of welfare loss that would result from TTIP.
BEUC, the European Consumer Organization, put forward many arguments against chlorination (Coynes, Reference Coynes2014), but the European Food Safety Agency (EFSA) itself had issued a scientific opinion proposing changes in the poultry meat inspection system (EFSA Panel on Biological Hazards, EFSA Panel of Contaminants in the Food Chain, and EFSA Panel on Animal Health and Welfare, 2012). Through inaccurate citing (BEUC made a generalization from the bacteria Campylobacter to all zoonotic pathogens, for which there is no support in EFSA’s article), BEUC inverted the content of EFSA’s opinion to support BEUC’s own view of the matter.
BEUC (Coynes, Reference Coynes2014) also turned around information from EFSA regarding the share of human cases of infection with Campylobacter that can be attributed to the different stages in the food value chain by inappropriately mixing up the results of different case studies in EFSA (EFSA Panel on Biological Hazards, 2010).
While BEUC remarked disparagingly about U.S. chicken (“chemically treated poultry”: Coynes, Reference Coynes2014), the European Medicines Agency (EMA, 2016) documented the use of antibiotics and other chemicals in European food production. Their figures showed that chicken production in Europe relied as much on antibiotics and other chemicals as other animal production lines. Even the European Parliament (2013) stated that it would be incorrect to view differences in food safety regulations in the EU and the United States as a general manifestation of fewer food safety concerns in the United States.
Matthews (Reference Matthews2016) argued that, in addition to the activities of the BEUC, the mainstream media also contributed to the provision of uncritical information. He provided examples from UK newspapers the Guardian and the Independent, which ran stories on the Greenpeace TTIP leaks without asking the European Commission for comments on the texts to provide balance, nor seeking to put the Greenpeace claims in context by querying independent experts for their opinions.
3. Model overview
There exists little economic literature covering the topic of (trade) negotiation transparency, and less exploring the issue of whether public transparency can ever have harmful effects. One exception is Morris and Shin (Reference Morris and Shin2002), who studied the social value of transparency in relation to central bank behavior and the financial markets. Stasavage (Reference Stasavage2004, Reference Stasavage2005, Reference Stasavage2007) developed game-theoretical models to argue that transparency may have public costs as well as public benefits. The driving force behind Stasavage’s results was that negotiators subject to close scrutiny might “posture.” Negotiations break down as negotiators try to convince the domestic public that they are loyal to the public interest and end up being unable to make needed compromises.
We argue that when representatives negotiate in public, they face incentives to use their actions as a signal of loyalty to their constituents, potentially ignoring private information about the true desirability of different policies. Anticipating this, constituents will not alter their prior policy beliefs following a debate of this type. When representatives instead make policy decisions in private, they are more likely to allow private information to influence their actions (Stasavage, Reference Stasavage2007). Diverging from Stasavage’s treatment, our analysis focuses on the costs to political agents of generating and processing information. These costs occur because political agents in our model observe facts and have the option to either pass them on to citizens unchanged (as “true information”) or “spin” them to mislead. Spinning facts is costly to the political agents, but if they succeed in convincing citizens of the truth of the information they have passed on, they benefit from the citizens’ choices made in their favor. Citizens lose welfare if they make choices based on misleading information but may discover the true content of the information through costly inspection. The costs of producing misleading information, the costs of inspecting information, and how often such information is passed to citizens determine the model’s equilibrium outcomes. In particular, the less frequently information is passed, the less welfare is reduced by costs of producing misleading information and inspecting.
We present three game-theoretical models that deal with the issues of transparency and misinformation in different settings. Transparency in the models is measured as the number of “facts” revealed to a citizen. More facts imply greater transparency. The first game introduces the basic elements of “spinning facts”: a citizen decides whether to “inspect” a fact to uncover potentially misleading information. The second game extends game 1 to the continuous case. In the third game, a second player (the interest group) is placed between nature and the citizen. The citizen no longer receives information directly from nature, but instead through the filter of the interest group, which may have spun a fact. When the game is played under institutional rules that allow more “facts” to be “spun,” equilibrium social welfare can be lower than under institutional rules in which fewer facts can be spun.
3.1. Game 1: a discrete choice model of citizen choices of facts among “spin”
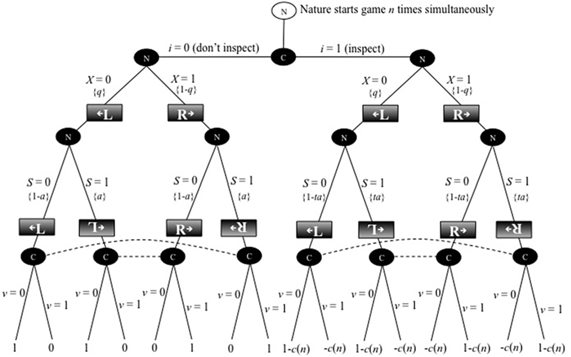
The first model is game 1, which is made up of n simultaneously played “one-fact” games (i.e., game 1.1, game 1.2, …, game 1.n). Figure 1 presents the extensive form of one-fact game 1.j. The n − 1 other one-fact games are identical to game 1.j. Game 1.j has two players: nature (N) and a citizen (C), and three periods. In period 1, the citizen decides whether to pay a per fact cost c(n) to “inspect” the results of upcoming plays by nature in the one-fact game. We assume ć(n) > 0; that is, the per fact cost of inspection is a monotonically increasing function of the number of facts that the citizen must inspect (i.e., in the number of one-fact games she must play simultaneously). This assumption represents the idea that the citizen’s fact-processing abilities are limited; limited brain power, time, energy, and so forth, make it so that when a citizen is confronted with the task of judging the veracity of many political claims, the more that must be judged, the less the amount of time, energy, and brain power that can be devoted to critically examining each claim.
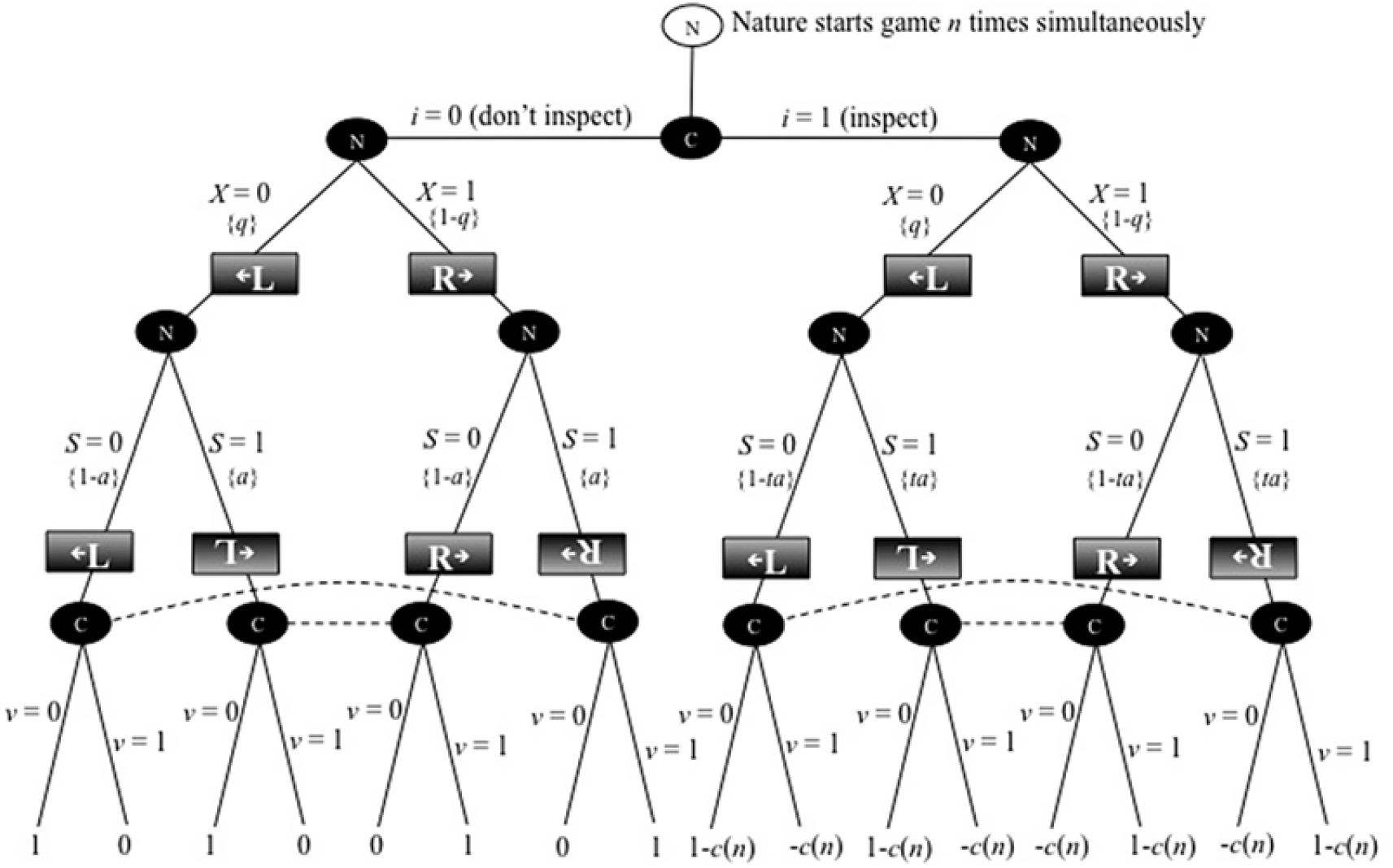
Figure 1. One of n identical one-fact games in game 1.
Period 2 of the one-fact game begins with nature drawing a “fact” from a binomial distribution of a random variable X. For any Q ∈ [0, 1], let b(X, Q) be the probability density function parameterized by Q:
When X = 0, we call X a “leftist fact,” and when X = 1, we call it a “rightist fact.” It will sometimes be useful to label facts by the symbols “←L” and “R→”.
At the same time that nature is generating the fact X, nature also chooses randomly whether to “spin” the fact. Consider another random variable, S (called “spin”), which is also generated from a binomial distribution parameterized by a real number a ∈ in [0, 1].
Consider the following function, which we call the “appearance function”:
When S = 0, the fact X is “not spun,” and so it “appears” as its own value. When S = 1, the fact X is “spun,” and so if the fact is actually 0, it “appears” to be 1, and if the fact is actually 1, it appears to be 0. We might illustrate an agent who is “not fooled by appearances” as seeing the following:
A(0, 0) = “←L”, A(0, 1) = “r→”, A(1, 0) = “R→”, and A(1, 1) = “←ᴚ”.
However, if the citizen is “fooled by appearances”, she simply sees the “arrows” and not the “letters” of the (spun or not spun) fact: A(0, 0) = “←”, A(0, 1) = “→”, A(1, 0) = “→”, and A(1, 1) = “←”. So, a spun fact appears as its opposite: a leftist fact appears to be rightist, and a rightist fact appears to be leftist. We assume that the citizen is “fooled by appearances.” We assume that the citizen knows the functional form of b(X, Q) and its domain but does not know the value of the draw q coming from the distribution. (We can call the value of q “the truth.”) If the citizen were to know the value of q, she would know b(X, q). We assume that the citizen also knows the probability with which facts are spun, a, and that spinning is generated by the binomial process defined in equation (2).
Next, we assume that the citizen’s objective is to observe a drawn (and potentially spun) fact and use it to estimate whether q is less than or equal to 0.5 and then use that estimate to “choose a government.” That is, the citizen is trying to figure out the “truth,” which may be leftist (if q ≤ 0.5) or rightist (if q > 0.5). If the truth is leftist, the consumer wants to choose a leftist government and does so by choosing v = 0. If the truth is rightist, the citizen wants to choose a rightist government by choosing v = 1.
Even though the citizen is fooled by appearances, we allow her to choose, at a cost, whether to “inspect” a “fact” (whether it has been spun or not). Her inspection choice variable is i, which when set to zero implies no inspection, and when set to one, the fact is inspected and “unspun.” That is, leftist facts that appeared to be rightist when not inspected are seen to be truly leftist after inspection, and rightist facts that appeared to be leftist when not inspected are revealed to be truly rightist after inspection. The cost of an inspection is c(n) > 0.
We assume that the citizen’s utility depends on whether she has chosen the correct kind of government. She receives one unit of utility (util) when she chooses government correctly (i.e., if she has chosen a leftist government if the truth is on the left and a rightist government if the truth is on the right). She receives no utils if she chooses government incorrectly. Her utility also depends on whether she has conducted an inspection. So the citizen’s utility is described by equation (4):
We assume that the citizen chooses whether to inspect facts and how to vote, with the objective of maximizing her expected utility. Her choices, their outcomes, and the model’s random elements are illustrated in Figure 1, which shows an extensive form of a two-player game, where the players are nature (N) and the citizen (C). The citizen makes the first move, deciding before the fact “appears” whether to inspect or not to inspect the fact. Nature then generates a fact, drawing a leftist fact with probability q or a rightist fact with probability 1 − q. Then nature spins the fact, with probability a, or does not spin it, with probability 1 − a. If, however, the citizen chooses to inspect a fact, it reduces the probability that a spun fact “stays spun.” That is, instead of being “spun” with probability a, a fact is “effectively spun” (i.e., “spun” but not “unspun”) with probability ta, where t ∈ (0, 1).
It can be shown that the citizen depicted in Figure 1 will choose to inspect the fact if c(n) < (1 − t)a. That is, letting an asterisk denote an ex ante optimal decision,
Note that the citizen is indifferent between inspecting and not inspecting if c(n) = (1 − t)a. The result shown in equation (5) is intuitive: The cost of inspecting a fact is c(n). The benefit of inspecting equals the value of choosing the correct government (which is 1) times the increase in the probability of finding a spin if one inspects, which is (1 − t)a. Because having to play additional one-fact games raises the per fact cost of inspection, it lowers the probability that the citizen installs the optimal government. For sufficiently high values of n, the per fact costs of inspection will be great enough to prevent the citizen from choosing to inspect the facts, and on average the government installed will deviate from the optimal government.
3.2. Game 2: a continuous choice model of citizen choices of facts among “spin”
Consider a random variable X = μ + ε, where μ is a constant real number, and ε ~ N(0, σ2 ). Assume that draws from the distribution of ε are independent. Interpret any value of X as representing a “fact” about the effects of government policy. When X < μ, the fact is “leftist,” and when X > μ, the fact is a “rightist.”
Next, consider a citizen who obtains utility by choosing a government. C’s choice variable is v, which must be chosen from the real number line. C desires to install a government that is not too far “left” or too far “right”; that is, C wants to install a government that balances leftist and rightist facts to develop a policy based on evidence from the facts at hand. The citizen’s utility function is
where K is a positive constant. When the citizen (C) chooses v, she does not know μ. Rather, she gains information about μ from draws of the random variable X out of its distribution. She knows that X is distributed normally but does not know the mean or variance of the distribution. In addition, C can learn about any fact by “inspecting it.” However, the inspection process is itself flawed, so that sometimes C perceives facts to be more “rightist” or more “leftist” than they actually are. C’s perceived value of a fact is determined by a random process, where the perceived value of a fact is its true value plus a normally distributed random variable: Y = X + ω, where the draws of ω are independent and identically distributed as ω ~ N(0, g(n)). Assume that g(n) is positive and monotonically increasing for all n. The idea is that the citizen is forced to inspect all the facts in a sample and must do so in a fixed amount of time or with a fixed amount of personal energy or resources. The greater the number (n) of facts inspected, the less time there is to spend on each fact, and so the greater is the variance of the size of the misjudgment. The citizen estimates μ by using the best unbiased estimate of it that is linear in the perceived values of the drawn facts. This is well known to be the sample mean:
Solving the utility maximization is equivalent to solving the following problem:
The solution to the abovementioned problem is to set v equal to
![]() $\hat \mu $
, which is the mean of the sample of perceived values of the drawn facts. Note that (ε + ω) ∽ N(0, σ2
+ g(n)). The statistical properties of
$\hat \mu $
, which is the mean of the sample of perceived values of the drawn facts. Note that (ε + ω) ∽ N(0, σ2
+ g(n)). The statistical properties of
![]() $\hat \mu $
under these assumptions are well known:
$\hat \mu $
under these assumptions are well known:
From equation (6), the realized utility of the consumer is
and expected utility is
 $E{U_C}\left( n \right) = K - E\left( {{{\left[ {\scale 150%{1 \over n}\sum\limits_{i = 1}^n {\left( {{\varepsilon _i} + {\omega _i}} \right)} } \right]}^{{\kern 1pt} 2}}} \right) = K - E\left( {\scale 150%{1 \over {{n^2}}}\left[ {\sum\limits_{i = 1}^n {\varepsilon _i^2 + \sum\limits_{i = 1}^n {\omega _i^2} } } \right]} \right) \hskip +30pt= K - \left( {\scale 150%{1 \over {{n^2}}}\sum\limits_{i = 1}^n {Var\left( {{\varepsilon _i}} \right)} } \right) - \left( {{1 \over {\scale 150%{n^2}}}\sum\limits_{i = 1}^n {Var\left( {{\omega _i}} \right)} } \right) = K - {{{\sigma ^2}} \over n} - {{g\left( n \right)} \over n}.$
$E{U_C}\left( n \right) = K - E\left( {{{\left[ {\scale 150%{1 \over n}\sum\limits_{i = 1}^n {\left( {{\varepsilon _i} + {\omega _i}} \right)} } \right]}^{{\kern 1pt} 2}}} \right) = K - E\left( {\scale 150%{1 \over {{n^2}}}\left[ {\sum\limits_{i = 1}^n {\varepsilon _i^2 + \sum\limits_{i = 1}^n {\omega _i^2} } } \right]} \right) \hskip +30pt= K - \left( {\scale 150%{1 \over {{n^2}}}\sum\limits_{i = 1}^n {Var\left( {{\varepsilon _i}} \right)} } \right) - \left( {{1 \over {\scale 150%{n^2}}}\sum\limits_{i = 1}^n {Var\left( {{\omega _i}} \right)} } \right) = K - {{{\sigma ^2}} \over n} - {{g\left( n \right)} \over n}.$
Finally, note the effect of an increase in the sample size on expected utility:
 $${{dE{U_C}\left( n \right)} \over {dn}} = {{d\left[ {K{{{\sigma ^2}} \over n}{{g(n)} \over n}} \right]} \over {dn}} = - \left( {{{{\sigma ^2}} \over {{n^2}}} + {{g\left( n \right) - ng'\left( n \right)} \over {{n^2}}}} \right) = {{g'\left( n \right)} \over n} - {{{\sigma ^2} + g\left( n \right)} \over {{n^2}}}.$$
$${{dE{U_C}\left( n \right)} \over {dn}} = {{d\left[ {K{{{\sigma ^2}} \over n}{{g(n)} \over n}} \right]} \over {dn}} = - \left( {{{{\sigma ^2}} \over {{n^2}}} + {{g\left( n \right) - ng'\left( n \right)} \over {{n^2}}}} \right) = {{g'\left( n \right)} \over n} - {{{\sigma ^2} + g\left( n \right)} \over {{n^2}}}.$$
Because g is increasing in n, the sign of the expression is ambiguous. That is, increasing the sample size may decrease expected utility. The intuition behind this result is that, ceteris paribus, although increasing the sample size n (i.e., obtaining additional “facts”) provides the citizen with a better estimate of the mean of the distribution of facts X (which is also the mean of the distribution of the perceived facts Y), increasing sample size leaves less time per fact for inspection and so can increase the variance of the estimate of μ and decrease the accuracy of the citizen’s estimate of the optimal government to be installed. Thus, more “facts” need not make the citizen better off; because the citizen has limited resources with which to inspect the facts to estimate their mean, her assessment of the “facts” may worsen as the sample size increases.
3.3. Game 3: a model in which one interest group spins facts
Finally, we present a model in which a biased interest group can spin facts in an effort to win the political support of a representative citizen. We call this game 3. Like game 1, game 3 consists of n simultaneously played “one-fact” games (i.e., game 3.1, …, game 3.n). We show the extensive form of one such one-fact game in Figure 2.

Figure 2. The external form of one of n one-fact games played between a fact-spinning interest group and a citizen.
Without loss of generality, we assume that the interest group, denoted GL , is leftist. Whether the truth is leftist or rightist depends once again on nature. When t = 0, the truth is leftist. When t = 1, the truth is rightist. GL observes the truth and decides whether to spin the fact to make it appear other than it is. The citizen then sees the appearance of the truth in all of the one-fact games and must decide whether to vote for a leftist or rightist government. Payoff functions are shown in equations (12) and (13).
Game 3 is a type of signaling game, and as is common with signaling games, we use the pure-strategy Bayesian Nash equilibrium concept (Gibbons, Reference Gibbons1992). There are four potential types of such equilibria for the game: (1) “never spin,” (2) “always spin,” (3) “spin when you shouldn’t and don’t spin when you should,” and (4) “spin when the truth is inconvenient.”
It can be shown that the only pure-strategy perfect Bayesian Nash equilibrium in this game is the “spin when the truth is inconvenient” strategy. In game 3, because the interest group is biased left, the truth is “inconvenient” when nature generates a rightist fact. Only in this case will the leftist interest group attempt to spin the fact—and the group will do this only in the case in which inspection costs are sufficiently high (above 0.5). Because again we assume that per fact inspection costs increase with the number of facts that must be inspected, when nature generates more than some number of facts, it no longer is profitable for the citizen to inspect the facts. As a result, the citizen is more likely to be fooled by the interest group’s “spinning” of the facts and install a government that is leftist, which lowers social welfare when the truth is rightist.
4. Summary and conclusions
The research that led to this article was first motivated by the EU’s increased public demand for more openness and transparency in EU-U.S. TTIP negotiations. Our purpose was to examine whether more government transparency necessarily leads to higher social welfare. We have presented three stylistic, game-theoretical political economy models in which the concept of transparency has been formally defined as “more facts” available to society. The results suggest that political institutions that allow interest groups to produce more facts may actually decrease social welfare. That is, more facts do not necessarily lead to “more information”—or at least not more usable information. The rationale behind this result is that the social process of mapping “facts” into policy decisions is complex and requires employment of scarce resources. If those scarce resources must be spread out to process more facts, that processing may be less efficient and, in the end, may result in a poorer public estimation of “reality” than would a more judicious public presentation of facts.
Given the history of authoritarianism in governments, it is not surprising that people living in representative democracies tend to favor—or at least think they favor—more government openness than less. We present models that suggest, however, that the “optimal government transparency” problem may not have a corner solution: it may not be desirable for government to be absolutely transparent in all that it does.
Recently, “fake news” has become an increasingly important social phenomenon, notably in the 2016 Brexit referendum, in the U.S. presidential election, and during the current U.S. presidency. If we are willing to see the news media as sometimes being controlled by interest groups, or at least as striving to please the interest groups that their audiences support, the models presented in this research can be applied to examine the welfare effects of one important cause of misleading information in politics—namely, the reduced costs of spreading such information. Moreover, if we are willing to think of social media and Internet political postings, whether true or false, as “news,” our models can be used to understand the effects of changes in information distribution technologies on the truthfulness of the information that the public receives. In the third model’s equilibrium, the amount of misleading information generated by a political interest group (or the news media outlets that appeal to that group) is inversely related to the cost of spinning facts. When interest groups and their news media partners can spin facts at lower costs, more misleading information will be signaled to citizens. The political impacts of the Internet and social media provide an example of this phenomenon. Today, a single mouse click is sufficient to send “fake news” to millions of citizens around the world. The cost of spinning facts has decreased, and, consequently, the amount of misleading information has risen. Although our models are characterized by simple structures, they capture essential features of this “fake news” process.
To conclude, we contend that the costs of spreading information will further decrease in the future because of technical progress in communication technology and more people having access to the means of communication. This development embodies the potential benefit of building confidence and trust by more people engaging in the political discourse, but it runs the potential risk of decreasing welfare as more of society’s resources are needed to detect misleading information and to prevent political decisions being made on misleading information.
Financial support
This work was supported (1) by the Research Council of Norway as part of the Basic Funding to the Norwegian Institute of Bioeconomy Research (NIBIO); (2) by U.S. Department of Agriculture, National Institute of Food and Agriculture’s Hatch Project 470 362; and (3) by the European Commission through the Jean Monnet Center of Excellence grant awarded to the University of Illinois European Union Center. This publication reflects the views of the author only, and the European Commission cannot be held responsible for any use that may be made of the information.