1. Introduction
Global demand for grains has been increasing in response to population growth, expanding economies in developing countries, and rising biofuel production, among other factors (Trostle, Reference Trostle2008). Irrigation of grain crops is expanding in humid regions of the world to meet growing global demand for grains (Mullen, Yu, and Hoogenboom, Reference Mullen, Yu and Hoogenboom2009; Rosegrant, Ringler, and Zhu, Reference Rosegrant, Ringler and Zhu2009; Schaible and Aillery, Reference Schaible and Aillery2012). Rosegrant, Ringler, and Zhu (Reference Rosegrant, Ringler and Zhu2009) predict that more than half of global cereal production will be under irrigation by 2050. In the United States, irrigation of grain crops in humid regions such as the Southeast has grown in the past several years (Banerjee and Obembe, Reference Banerjee and Obembe2013; Salazar et al., Reference Salazar, Hook, Garcia y Garcia, Paz, Chaves and Hoogenboom2012; Schaible and Aillery, Reference Schaible and Aillery2012; Vories et al., Reference Vories, Tacker, Lancaster and Glover2009). Schaible and Aillery (Reference Schaible and Aillery2012) found that the largest increase in irrigated crop production has been in the southeastern states of Alabama, Georgia, and Mississippi, with corn having the largest expansion in irrigated acres since 1998 (Salazar et al., Reference Salazar, Hook, Garcia y Garcia, Paz, Chaves and Hoogenboom2012; Vories et al., Reference Vories, Tacker, Lancaster and Glover2009).
Most humid regions of the United States receive enough annual rainfall to produce corn without irrigation, but the purpose of irrigation is to supplement rainfed corn production during periodic short-term droughts. Timely supplemental irrigation in humid regions can provide many agronomic benefits such as increasing yields (Bruns, Meredith, and Abbas, Reference Bruns, Meredith and Abbas2003; Smith and Riley, Reference Smith and Riley1992), decreasing crop disease (Smith and Riley, Reference Smith and Riley1992; Vories et al., Reference Vories, Tacker, Lancaster and Glover2009), and stabilizing yields (Apland, McCarl, and Miller, Reference Apland, McCarl and Miller1980; Dalton, Porter, and Winslow, Reference Dalton, Porter and Winslow2004; Evans and Sadler, Reference Evans and Sadler2008; Salazar et al., Reference Salazar, Hook, Garcia y Garcia, Paz, Chaves and Hoogenboom2012; Vories et al., Reference Vories, Tacker, Lancaster and Glover2009).
Economic research on irrigation in humid regions has primarily focused on the benefits from managing production risk through higher and more stable yields. Early research by Boggess et al. (Reference Boggess, Lynne, Jones and Swaney1983) and Boggess and Amerling (Reference Boggess and Amerling1983) found that irrigation maximized crop net returns and reduced production risk under Florida growing conditions. However, Boggess et al. (Reference Boggess, Lynne, Jones and Swaney1983) found that if crop prices decreased below a certain threshold, the cost of irrigation was greater than the benefits from irrigation; thus, crop prices needed to remain above this threshold for irrigation to be feasible. Boggess, Anaman, and Hanson (Reference Boggess, Anaman and Hanson1985) surveyed farmers in the southeastern United States and found that irrigation was the most common risk management response to rainfall variability. In a more recent study, Dalton, Porter, and Winslow (Reference Dalton, Porter and Winslow2004) compared irrigation with crop insurance to manage potato production risk in the northeastern United States. They found that crop insurance was risk inefficient and supplemental irrigation was risk efficient depending on the scale (i.e., field size) of the system, with a larger scale providing more risk management benefits. DeJonge, Kaleita, and Thorp (Reference DeJonge, Kaleita and Thorp2007) assessed the potential for irrigating corn in Iowa and calculated a breakeven corn price of $4.60/bu. for irrigation on a 125-acre field. They concluded that irrigation was not profitable given the expected corn price of $2/bu. used in the analysis.
Although the previously mentioned studies provide useful insights, the profitability and risk of irrigating corn in humid regions has likely changed with higher corn prices in recent years. The primary driver of the upward shift in corn prices since 2006 has been the subject of extensive debate, but most analysts agree that multiple factors were involved (de Gorter, Drabik, and Just, Reference de Gorter, Drabik and Just2013; Trostle, Reference Trostle2008). Some analysts have described the confluence of growing demand for grains, rising meat consumption, expanding biofuel production, and increasing cost of production as the “perfect storm” of events that caused the price of corn to rise (de Gorter, Drabik, and Just, Reference de Gorter, Drabik and Just2013; Trostle, Reference Trostle2008). Mullen, Yu, and Hoogenboom (Reference Mullen, Yu and Hoogenboom2009), using a multicrop production model for the southeastern United States, found that energy cost slightly influenced irrigation water demand, but crop prices had the greatest influence on irrigation water demand. The profitability and risk of investing in an irrigation system for corn production in a humid region is unknown for the higher corn prices of recent years.
Additionally, the aforementioned studies used simulated yield data and excluded inputs other than water (Boggess and Amerling, Reference Boggess and Amerling1983; Boggess et al., Reference Boggess, Lynne, Jones and Swaney1983; Dalton, Porter, and Winslow, Reference Dalton, Porter and Winslow2004; DeJonge, Kaleita, and Thorp, Reference DeJonge, Kaleita and Thorp2007). Along with water, nitrogen (N) fertilizer is considered to be the most important input in corn production (Stone et al., Reference Stone, Camp, Sadler, Evans and Millen2010), providing the highest return per dollar spent (Pikul, Hammack, and Riedell, Reference Pikul, Hammack and Riedell2005). Water and N fertilizer are complements in crop production; thus, irrigation will likely increase both yield and the profit-maximizing N fertilization rate (Dinnes et al., Reference Dinnes, Karlen, Jaynes, Kasper, Hatfield, Colvin and Cambardella2002; Stone et al., Reference Stone, Camp, Sadler, Evans and Millen2010; Vickner et al., Reference Vickner, Hoag, Frasier and Ascough1998). Using nonprofit-maximizing N fertilization rates and yields could misrepresent returns to irrigation. For instance, if net returns were compared assuming that 150 lb./ac. of N was applied to both nonirrigated and irrigated corn, the net returns from irrigating corn might be underestimated because irrigated corn will likely require more N fertilizer than nonirrigated corn (Dinnes et al., Reference Dinnes, Karlen, Jaynes, Kasper, Hatfield, Colvin and Cambardella2002; Stone et al., Reference Stone, Camp, Sadler, Evans and Millen2010; Vickner et al., Reference Vickner, Hoag, Frasier and Ascough1998). Thus, selecting the profit-maximizing N fertilization rates for nonirrigated and irrigated corn levels the playing field for yields and returns to irrigation. To avoid misstating the profitability of irrigation, the physical relationship between yield, irrigation, and N should be considered.
We calculated the expected net present value (NPV) and the probability of a positive NPV of investing in a center-pivot irrigation system for corn production for three field sizes and two energy sources in Tennessee. Monte Carlo simulation was conducted using corn, N, and energy prices from 1994 to 2013. We also simulated the model using prices for the 1994–2005 and 2006–2013 periods to analyze the impact of the shift in corn prices. We used actual field-experiment data to estimate stochastic yield response to N fertilizer for nonirrigated and irrigated corn. Profit-maximizing yields and N rates were used to determine net returns for nonirrigated and irrigated corn. Little is known about the importance of economics of scale with respect to investing in an irrigation system and selecting an energy source; thus, this study will hopefully assist extension personnel and producers to determine whether irrigating corn is profitable in a humid region of Tennessee for different field sizes and energy sources.
2. Data
Corn N fertilization experiments were conducted at the University of Tennessee Milan Research and Education Center (35°56′ N, 88°43′ W) from 2006 to 2012. Nonirrigated corn was produced on a Grenada soil (fine-silty, mixed, active, thermic Oxyaquic Fraglossudalfs), and irrigated corn was grown on a Loring soil (fine-silty, mixed, active, thermic Oxyaquic Fragiudalfs). Both soils were considered highly suitable for corn production in Tennessee. Pioneer 33N58 was planted in 76 cm rows in April in rotation with soybeans (corn following soybeans) on fields that have been under no-till production for more than a decade (Yin et al., Reference Yin, McClure, Jaja, Tyler and Hayes2011).
The experimental design was a randomized complete block with five or six N fertilization treatments and four replications. The annual N fertilization rates were 0, 55, 110, 165, and 220 lb./ac. in 2006 and 2007. In 2008, a treatment of 275 lb./ac. was added to the experiments. Ammonium nitrate was uniformly broadcast on the soil surface around planting time. Phosphorus and potassium were applied based on University of Tennessee soil-test recommendations. Each plot was 15 feet wide and 30 feet long. All other production inputs, such as weed, pest, and disease control, were similar for the nonirrigated and irrigated experiments and followed the University of Tennessee's recommended management practices. Table 1 shows the average yield and N rate by year.
Table 1. Average Corn Yields (Bushels per Acre) for Nonirrigated and Irrigated Corn by Year

Note: Yields are averaged across replications.
Average irrigation totals applied by month are presented in Table 2. Supplemental water was uniformly applied to the irrigated plots using a Valley linear irrigation system (Valmont Irrigation, Valley, NE). The supplemental water rates were based on the “Management of Irrigation Systems in Tennessee” (MOIST) soil moisture management system program, which is an online irrigation scheduler available for corn producers in Tennessee (Leib, Reference Leib2012b). The data indicate that 2007 and 2012 were drought years, requiring early season supplemental irrigation in May of each of those two years, and 2009 was an abundant-rainfall year, reducing the total amount of supplemental irrigation compared with other years.
Table 2. Average Irrigation Rate (Acre-Inches per Year) Applied by Month, Milan, Tennessee, 2006–2012
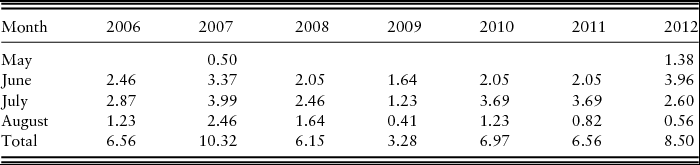
Sources: National Oceanic and Atmospheric Administration, Milan, Tennessee, weather station; and MOIST (Leib, 2012b).
Prices used in the simulations were from 1994 to 2013 and converted into 2013 dollars using the seasonally adjusted annual “Gross Domestic Product: Implicit Price Deflator” (Federal Reserve Bank of St. Louis, 2013). Tennessee corn and N prices were collected from the U.S. Department of Agriculture, National Agricultural Statistics Service (USDA-NASS, 2013). U.S. diesel and electricity prices were collected from the U.S. Energy Information Administration (US-EIA, 2013). The averages and standard deviations of the prices are displayed in Table 3 for the different simulation periods.
Table 3. Average Prices and Standard Deviations Used in the Simulations by Time Period

Sources: USDA-NASS (2013) and US-EIA (2013).
Note: Standard deviations are in parentheses.
3. Irrigation System
3.1. Investment
The cost of irrigation equipment varies by field size, well depth, and energy source. We generalized the cost of irrigating corn by estimating the cost of a typical nontowable, center-pivot system. Nonirrigated and irrigated field sizes of 60 acres, 125 acres, and 200 acres were selected to reflect the range of field sizes in Tennessee. Table 4 shows the capital investment by well expense and system investment. Estimated investment costs were from actual bid prices for installing a nontowable center-pivot system in west Tennessee provided by a west Tennessee irrigation dealership and personal communication with an irrigation extension specialist in west Tennessee (Verbree, Reference Verbree2012). Economies of scale for the investment cost of an irrigation system were found for the three field sizes, which has important implications for profitability of the investment.
Table 4. Center-Pivot Investment Costs (US$) by Field Size

aThis is the base cost by item for the irrigation equipment. When electric energy is used, three additional fixed costs to run electricity to the well were included in the fixed cost.
Sources: Personal communication with irrigation dealerships in west Tennessee and an irrigation expert (Verbree, Reference Verbree2012).
We assumed that the center-pivot system had a 20-year useful life and zero salvage value, which follows the assumptions of Ding and Peterson (Reference Ding and Peterson2012) and Guerrero et al. (Reference Guerrero, Amosson, Marek and Johnson2010). We also assumed that the producer financed the cost of the well and system over 5 years at a 5% interest rate, which is what Guerrero et al. (Reference Guerrero, Amosson, Marek and Johnson2010) used. The total capital investment cost of the equipment was depreciated under the Modified Accelerated Cost-Recovery System over 5 years at a 25% marginal tax rate. Finally, the risk-adjusted discount rate was 1.5%, which is lower that what other irrigation investment studies have used (Carey and Zilberman, Reference Carey and Zilberman2002; Guerrero et al., Reference Guerrero, Amosson, Marek and Johnson2010; Seo et al., Reference Seo, Segarra, Mitchell and Leatham2008) but reflects the current real discount rate (U.S. Department of the Treasury, 2013).
3.2. Operation
A preliminary review of the data suggested that irrigation requirements vary across years. Taking a simple average of irrigation rates would overweight the high irrigation requirements for the 2007 and 2012 drought years and the low irrigation requirements for 2009 when timely rainfall occurred. Therefore, we weighted annual irrigation rates from the experiment to calculate the expected irrigation rate. We follow Lambert, Lowenberg-DeBoer, and Malzer's (Reference Lambert, Lowenberg-DeBoer and Malzer2007) method of creating annual weights based on the irrigation data. In our model, the annual weights (θt
) were determined as
![]() $\theta _t = {{\prod\nolimits_t {\phi (w_t )} } / {\sum\nolimits_{t = 0}^T {\prod\nolimits_t {\phi (w_t )} } }}$
, where wt
is the total irrigation water observed in year t (t = 1, . . ., T) and ϕ(wt
) is the standard normal probability density function. The weighting is based on the rule of probability multiplication and assumes that the irrigation rate in year t is independent of the rates in other periods (Lambert, Lowenberg-DeBoer, and Malzer, Reference Lambert, Lowenberg-DeBoer and Malzer2007). The expected irrigation rate was
$\theta _t = {{\prod\nolimits_t {\phi (w_t )} } / {\sum\nolimits_{t = 0}^T {\prod\nolimits_t {\phi (w_t )} } }}$
, where wt
is the total irrigation water observed in year t (t = 1, . . ., T) and ϕ(wt
) is the standard normal probability density function. The weighting is based on the rule of probability multiplication and assumes that the irrigation rate in year t is independent of the rates in other periods (Lambert, Lowenberg-DeBoer, and Malzer, Reference Lambert, Lowenberg-DeBoer and Malzer2007). The expected irrigation rate was
![]() $w = \sum\nolimits_{t = 1}^T {\theta _t } w_t$
. An expected irrigation rate of 6.88 acre-inches per year was found with a standard deviation of 2.16 acre-inches per year. This rate was close to the same as the average annual irrigation rate of 6.90 acre-inches per year reported in the 2007 Census of Agriculture: Farm and Ranch Irrigation Survey (2008) for Tennessee (USDA, 2010).
$w = \sum\nolimits_{t = 1}^T {\theta _t } w_t$
. An expected irrigation rate of 6.88 acre-inches per year was found with a standard deviation of 2.16 acre-inches per year. This rate was close to the same as the average annual irrigation rate of 6.90 acre-inches per year reported in the 2007 Census of Agriculture: Farm and Ranch Irrigation Survey (2008) for Tennessee (USDA, 2010).
An important decision for producers in the southeastern United States is whether to use diesel or electricity to power their irrigation system. The annual energy costs of using diesel and electric power to apply the expected irrigation rate were calculated following Rogers and Alam's (Reference Rogers and Alam2006) energy cost formulas. These equations consider well depth, operating pressure, energy source, and field size in finding total energy used and the cost of the energy required. A weighted-average pump operating pressure of 39 pounds per square inch was chosen using data from the 2007 Census of Agriculture: Farm and Ranch Irrigation Survey (2008) (USDA, 2010), and an average pump-lift distance of 250 feet was used, which is a typical well depth in Tennessee (USDA, 2010; Verbree, Reference Verbree2012). Leib (Reference Leib2012a) showed the importance of including the fixed cost of running electricity to the pump; therefore, we used three fixed costs of $10,000, $15,000, and $20,000 to run electricity to the pump. The cost of running electricity to the field to power the well is not well known due to many factors such as access point of electricity and distance of line required. These costs are assumed to be an appropriate range of costs (Leib, Reference Leib2012a).
Jensen (Reference Jensen1980) and McGrann (Reference McGrann, Olson, Powell and Nelson1986a, Reference McGrann, Olson, Powell and Nelson1986b) estimated annual repair and maintenance costs for irrigation equipment as a percentage of the initial cost of the equipment, as proposed in the American Agricultural Economics Association (AAEA) Commodity Costs and Returns Estimation Handbook (2000). We calculated repair and maintenance costs using 1.7% of the initial cost, which is within the range stated in the AAEA handbook (2000). We assumed an annual irrigation labor cost of $12/ac., including labor costs for monitoring soil water status and other irrigation management activities that are typical for Tennessee (The University of Tennessee Agricultural and Resource Economics Department, 2013).
3.3. Simulation Framework
To estimate the expected NPV and the probability of a positive NPV, we first established the expected annual net returns to N for corn production for nonirrigating and irrigating corn producers using partial budgets:
where
![]() $E(\tilde \pi _\lambda )$
is the expected net return in dollars per acre, λ is a binary variable with λ = 1 for irrigation and λ = 0 for nonirrigation,
$E(\tilde \pi _\lambda )$
is the expected net return in dollars per acre, λ is a binary variable with λ = 1 for irrigation and λ = 0 for nonirrigation,
![]() $\tilde p$
is the uncertain price of corn in dollars per bushel, y
λ(x
λ) is yield in bushels per acre and is a function of the N fertilizer rate xλ
in pounds per acre,
$\tilde p$
is the uncertain price of corn in dollars per bushel, y
λ(x
λ) is yield in bushels per acre and is a function of the N fertilizer rate xλ
in pounds per acre,
![]() $\tilde r$
is the uncertain price of N fertilizer in dollars per pound,
$\tilde r$
is the uncertain price of N fertilizer in dollars per pound,
![]() $\tilde c$
is the uncertain cost of energy for pumping water in dollars per inches per acre, w is the expected irrigation water rate in inches per acre, l is the expected labor cost for monitoring soil water status and other labor activities related to irrigation in dollars per acre, and m is irrigation maintenance and repair costs in dollars per acre. We used a partial budget because other inputs are not likely to vary across nonirrigated and irrigated corn.
$\tilde c$
is the uncertain cost of energy for pumping water in dollars per inches per acre, w is the expected irrigation water rate in inches per acre, l is the expected labor cost for monitoring soil water status and other labor activities related to irrigation in dollars per acre, and m is irrigation maintenance and repair costs in dollars per acre. We used a partial budget because other inputs are not likely to vary across nonirrigated and irrigated corn.
We estimated yield response functions for nonirrigated and irrigated corn to determine the respective profit-maximizing N rates. Recently, many researchers have that found stochastic plateau response functions are more suitable than their deterministic plateau response function counterparts (Biermacher et al., Reference Biermacher, Brorsen, Epplin, Solie and Raun2009; Boyer et al., Reference Boyer, Larson, Roberts, McClure, Tyler and Zhou2013; Tembo et al., Reference Tembo, Brorsen, Epplin and Tostão2008; Tumusiime et al., Reference Tumusiime, Brorsen, Mosali, Johnson, Locke and Biermacher2011). Data from the experiments were used to estimate linear response stochastic plateau (LRSP) functions by Tembo et al. (Reference Tembo, Brorsen, Epplin and Tostão2008) for nonirrigated and irrigated corn:
where yti is the corn yield in bushels per acre in year t on plot i, β 0 and β 1 are the yield response parameters, xti is the quantity of N fertilizer applied in pounds per acre in year t on plot i, μ is the expected plateau yield in bushels per acre, ut ~ N(0, σ2 u ) is the year t plateau random effect, vt ~ N(0, σ2 v ) is the year t intercept random effect, and ε ti ~ N(0, σ2 e ) is the random error term in year t on plot i. The intercept parameter explains the expected yield when zero N fertilizer was applied, the slope parameter measures yield gains from an additional unit of N fertilizer, and the plateau parameter demonstrates the yield when N fertilizer is no longer a limiting input of yield. Independence is assumed across the three stochastic components. Because irrigation was applied as needed to supplement rainfall and did not follow prescribed rates in the experiment, the irrigation amounts were not included in the response functions. Equation (2) was estimated using the NLMIXED procedure in SAS 9.1 (SAS Institute Inc., 2003).
The profit-maximizing N fertilization rate is as follows (Tembo et al., Reference Tembo, Brorsen, Epplin and Tostão2008):
where Zα
is the standard normal probability of
![]() $\tilde r/(\tilde p\beta _1 )$
at the α significance level. The profit-maximizing expected yield is the following (Tembo et al., Reference Tembo, Brorsen, Epplin and Tostão2008):
$\tilde r/(\tilde p\beta _1 )$
at the α significance level. The profit-maximizing expected yield is the following (Tembo et al., Reference Tembo, Brorsen, Epplin and Tostão2008):
where Φ = Φ[a – μ/σu ] is the cumulative normal distribution function, a = β0 + β1 x, and ϕ = ϕ[a – μ/σu ] is the standard normal density function. Note that the expected yield (equation 4) and the profit-maximizing N fertilization rate (equation 3) are functions of the prices of corn and N, respectively; thus, the optimal expected yield and N fertilization rate change in the simulation as the prices of corn and N change, respectively.
Expected annual cash flows were calculated for a corn producer who finances the purchase of the irrigation system and for the one who does not invest in irrigation. Depreciation and annual interest were subtracted from net returns (equation 1) to calculate total taxable net returns:
where
![]() $\tilde K_\lambda$
is the annual taxable net returns, Dep is the annual depreciation of the irrigation system, and Int is the annual interest payment on the loan. The total taxable net returns were multiplied by the marginal tax rate to determine the annual amount paid in taxes. Annual cash flows were determined by subtracting annual loan payment for the irrigation system and the annual tax payment from the net returns:
$\tilde K_\lambda$
is the annual taxable net returns, Dep is the annual depreciation of the irrigation system, and Int is the annual interest payment on the loan. The total taxable net returns were multiplied by the marginal tax rate to determine the annual amount paid in taxes. Annual cash flows were determined by subtracting annual loan payment for the irrigation system and the annual tax payment from the net returns:
where
![]() $\tilde F_\lambda$
is the annual cash flow, PMT is the annual loan payment for the irrigation system, and τ is the annual tax rate.
$\tilde F_\lambda$
is the annual cash flow, PMT is the annual loan payment for the irrigation system, and τ is the annual tax rate.
Expected annual cash flows for nonirrigated and irrigated corn were simulated for the 20-year useful life of the irrigation system:
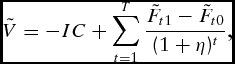 \begin{equation}
\tilde V = - IC + \sum\limits_{t = 1}^T {\frac{{\tilde F_{t1} - \tilde F_{t0} }}{{(1 + \eta )^t }}} ,\end{equation}
\begin{equation}
\tilde V = - IC + \sum\limits_{t = 1}^T {\frac{{\tilde F_{t1} - \tilde F_{t0} }}{{(1 + \eta )^t }}} ,\end{equation}
where
![]() $\tilde V$
is the NPV of the investment into the irrigation equipment, IC is the initial investment in irrigation equipment in year t = 1,
$\tilde V$
is the NPV of the investment into the irrigation equipment, IC is the initial investment in irrigation equipment in year t = 1,
![]() $\tilde F_{t1}$
is the annual cash flow for irrigated corn,
$\tilde F_{t1}$
is the annual cash flow for irrigated corn,
![]() $\tilde F_{t0}$
is the annual cash flow for nonirrigated corn, T = 20 is the useful life of the irrigation equipment, and η is the risk-adjusted discount rate. The discount rate was the producer's opportunity cost of investing in the irrigation equipment, representing the net return a producer would receive from an alternative investment (i.e., the Treasury bond). The discount rate was equal to the risk-free discount rate plus the risk premium (Seo et al., Reference Seo, Segarra, Mitchell and Leatham2008). If NPV = 0, the present value of the net cash flow from irrigating corn equals the opportunity cost of irrigating corn (i.e., the benefit from an alternative investment), and the producer is indifferent between investing in the irrigation system and an alternative investment. If NPV > 0, the producer would enhance net returns by investing in the irrigation system instead of the alternative investment. The annual cash flows were simulated for a 20-year useful life of the irrigation investment to calculate equation (7). NPV (equation 7) was simulated 5,000 times, and the results were used to determine the probability that NPV > 0.
$\tilde F_{t0}$
is the annual cash flow for nonirrigated corn, T = 20 is the useful life of the irrigation equipment, and η is the risk-adjusted discount rate. The discount rate was the producer's opportunity cost of investing in the irrigation equipment, representing the net return a producer would receive from an alternative investment (i.e., the Treasury bond). The discount rate was equal to the risk-free discount rate plus the risk premium (Seo et al., Reference Seo, Segarra, Mitchell and Leatham2008). If NPV = 0, the present value of the net cash flow from irrigating corn equals the opportunity cost of irrigating corn (i.e., the benefit from an alternative investment), and the producer is indifferent between investing in the irrigation system and an alternative investment. If NPV > 0, the producer would enhance net returns by investing in the irrigation system instead of the alternative investment. The annual cash flows were simulated for a 20-year useful life of the irrigation investment to calculate equation (7). NPV (equation 7) was simulated 5,000 times, and the results were used to determine the probability that NPV > 0.
Prices were drawn from a multivariate normal distribution, [p,r,c]~N(0, Σ), where Σ = TT′. As an example, the random draws for the price of corn were determined as
![]() ${\bf \tilde p} = \bar p + {\bf Tz}$
with z random draws and an average corn price of
${\bf \tilde p} = \bar p + {\bf Tz}$
with z random draws and an average corn price of
![]() $\bar p$
(Greene, Reference Greene2008). The cost data for the irrigation system and parameter estimates for equations (3) and (4) were substituted into the simulation model (equations 1–7) along with the equations for the randomly drawn prices for corn, N, and energy.
$\bar p$
(Greene, Reference Greene2008). The cost data for the irrigation system and parameter estimates for equations (3) and (4) were substituted into the simulation model (equations 1–7) along with the equations for the randomly drawn prices for corn, N, and energy.
4. Results
4.1. Yield Response Functions
Table 5 presents the parameter estimates for the LRSP functions for nonirrigated and irrigated corn. All parameter estimates were significant (P ≤ 0.05). The intercept parameter estimates suggest the expected yield for irrigated corn was 23 bu./ac. higher than for nonirrigated corn when zero N fertilizer was applied. Slope parameter estimates (yield response to N fertilizer) were similar for irrigated and nonirrigated corn, suggesting that irrigated and nonirrigated corn responded similarly to N fertilizer. The estimated plateau was 63 bu./ac. higher for irrigated corn than for nonirrigated corn, demonstrating the expected yield gain from timely application of irrigation. The plateau random effect was smaller for irrigated corn than for nonirrigated corn, indicating that year-to-year yield variability was reduced with irrigation. The reduction in plateau yield variability with irrigation shows a reduction in production risk.
Table 5. Estimated Corn Yield Response to Nitrogen (N) for Nonirrigated and Irrigated Corn Grown after Soybeans Using a Linear Response Stochastic Plateau Function

Note: Asterisks (***, **) indicate significance at P = 0.01 and P = 0.05, respectively.
The expected profit-maximizing N fertilizer rates (equation 3) and the expected profit-maximizing yields (equation 4), calculated from the estimated LRSP functions, are presented in Table 6 for each time period. The profit-maximizing yield for irrigated corn was 61 bu./ac. higher than for nonirrigated corn, and the profit-maximizing N rate for irrigated corn was 32 lb./ac. higher than for nonirrigated corn for all time periods. The profit-maximizing N rates were similar to the University of Tennessee recommendation for corn based on expected yield (Savoy and Joines, Reference Savoy and Joines2009). These findings demonstrate how assuming similar N rates for nonirrigated and irrigated corn can result in misleading net returns and over- or understating the profitability of investing in irrigation. In the simulation model, the LRSP function was embedded in the simulation model so that as the prices of corn and N changed, the profit-maximizing N rates and corn yields did as well.
Table 6. Expected Profit-Maximizing Yields and Nitrogen (N) Rates for Nonirrigated and Irrigated Corn by Time Period

4.2. NPV Results
Table 7 displays the expected NPVs for investing in irrigation and the probability of the investment's NPV being positive for the three time periods, three field sizes, and two energy sources. We present these results to show a more long-run answer to the feasibility of irrigating corn in Tennessee.
Table 7. Expected Net Present Value (NPV) of Investing in Irrigation and Probability that the Expected NPV Is Positive by Time Period, Field Size, and Energy Source

aThese numbers are the expected NPVs for investing in an irrigation system over a 20-year useful life, given the average prices for each time period.
bThese numbers are the probabilities that the expected NPVs are greater than zero for investing in an irrigation system over a 20-year useful life, given the average prices for each time period.
Note: Negative values are in parentheses.
Using prices from 1994 to 2013, expected NPV was negative for all energy sources on the 60-acre field with a zero probability of the NPV being greater than zero. Expected NPV was highest for using electric energy on the 60-acre field when the cost of running electricity to the pump was $10,000. If the cost of running electricity to the well exceeded $10,000, then the expected NPV was higher when using diesel. For the 125-acre field, expected NPV was negative for all energy sources. The probability of a positive NPV was 3% when diesel was the energy source and ranged from 11% to 31% depending on the fixed cost of running electrical energy to the well. The expected NPV was higher for electric power than for diesel regardless of the fixed cost of running electricity to the irrigation unit. Irrigating the 200-acre field using electric power produced the only scenarios where expected NPV was positive for 1994–2013 average prices. NPV ranged from $39,458 when the fixed cost of running electricity to the well was $20,000 to $62,069 when the fixed cost of running electricity to the well was $10,000. The probability of a NPV greater than zero was 78% to 89% for electric energy. When using diesel energy, the NPV was negative and the probability of NPV being positive was 39%. Overall, investing in supplement irrigation for corn production, given 1994–2013 average prices, would likely be infeasible on Tennessee corn fields less than 200 acres. The results demonstrate the importance of economies of scale when investing into irrigation system for corn production.
For prices between 1994 and 2005, expected NPV was negative for all field sizes and energy sources. Producers would be better off investing their money in U.S. Treasury bonds (the alternative investment). The expected NPV was highest for diesel energy on the 60-acre field, and the probability of NPV > 0 was zero for all energy sources on the 60-acre and 125-acre fields. The probability of NPV > 0 ranged from 1% to 5% on the 200-acre field. However, expected NPV was higher for electric power than for diesel when the fixed cost of running electricity to the well was $15,000 or less. For the 200-acre field, the fixed cost of electrical energy setup was spread over enough acres to make electrical power competitive with diesel energy. Using prices that prevailed during the 1994–2005 period, investment in supplemental irrigation for corn production would be infeasible.
Given prices after 2006, expected NPV increased for all field sizes and energy sources. For the 60-acre field, expected NPV was still negative, and the probability of NPV > 0 was still zero for all energy scenarios. The simulation result indicates that even at the current high prices, irrigating corn on a 60-acre field in Tennessee would likely have a negative NPV. Electric power with a fixed cost of running electricity to the well of $15,000 or less has a higher NPV than diesel energy on the 60-acre field. This result was different from the pre-2006 price scenario in which diesel was the preferred energy source. Expected NPV for the 125-acre field was $37,182 when diesel was the energy source and ranged from $67,215 to $89,827 when electrical energy was used, depending on the electrical setup cost. The probability of NPV > 0 ranged from 97% to 99% for electric energy and 87% for diesel energy. If a corn producer invested in an irrigation system on a 125-acre field, given prices that prevailed during the 2006–2013 period, the probability of NPV > 0 would be between 87% and 99%. Expected NPV for a 200-acre field was positive for all energy sources and ranged from $207,542 to $230,153 when electrical energy was used, and the probability of NPV > 0 was 100% regardless of the fixed cost. The expected NPV was $132,354 when diesel was the energy source, and the probability of NPV > 0 was 99%. Results for the preferred energy source on the 200-acre field are similar to the results for the 125-acre field—the producer's NPV was higher using electric power.
5. Discussion
Historically, investment in irrigation for corn production in Tennessee has been limited relative to other states in the southeastern states region. At the field level, an important factor that can influence the profitability and use of irrigation in the southeastern states is the difference in landscapes across the region. The flat topography in the Mississippi Delta of Arkansas, Louisiana, and Mississippi is conducive to irrigation (U.S. Geological Survey, 2013), with 79%, 41%, and 39% of harvested corn area irrigated in those states, respectively (USDA-NASS, 2013). In contrast, the rolling uplands of western Kentucky, western Tennessee, eastern Mississippi, and northern Alabama have smaller and more irregularly shaped fields that can make irrigation more costly (U.S. Geological Survey, 2013). Thus, only 9%, 2%, and 3% of harvested corn area is irrigated in Alabama, Kentucky, and Tennessee, respectively (USDA-NASS, 2013). Specifically, center-pivot irrigation systems are more expensive to install on the smaller and more irregularly shaped fields that are common in the eastern United States (Hatch et al., Reference Hatch, Hardey, Rochester and Pickren1991). Simulation results for the 1994–2013 price scenario show that a field has to be larger than 200 acres to have a positive expected NPV due to the economies of scale. Because Tennessee has few 200-plus-acre corn fields, this might explain why investment in corn irrigation has been historically lower than in most other southeastern states.
Nevertheless, investment in corn irrigation has been expanding in Tennessee. The simulation results indicate that the recent upward shift in corn, energy, and N prices have increased the likelihood of profitable investment in irrigation by corn producers. After the upward shift in prices in 2006, the likelihood of NPV being positive was still zero on fields of 60 acres or smaller, but the probability of NPV being positive was greater than 87% on fields of 125 acres or larger. Currently, the price of corn is historically high, but corn producers in Tennessee who invest in irrigation systems should be cautious about the risk of a decrease in future corn prices. The Food and Agricultural Policy Research Institute (FAPRI, 2012) has forecasted the price of corn to remain between $5/bu. and $6.50/bu. through 2022. At these forecasted prices over the next 10 years, investment in a center-pivot system could be profitable for corn fields larger than 125 acres. However, agricultural prices historically have experienced boom and bust periods (Gouel, Reference Gouel2012). If corn prices shift back to historical averages, then investment in corn irrigation will not likely be profitable in Tennessee. Using a real-option approach may be helpful to understand the dynamics of investing in an irrigation system for corn production.
Furthermore, the discount rate used in this analysis reflects the current real discount rate but is lower than other irrigation investment studies. If the discount rate increases, the profitability of investing in corn irrigation will decrease. Also, energy prices are not likely to decrease in the future and can impact the amount of water pumped by producers (Pfeiffer and Lin, Reference Pfeiffer and Lin2014). Our findings suggest that corn prices will likely need to remain high and the discount rate will need to remain low for extended periods of time for irrigated corn production to remain profitable in Tennessee. Further research is needed into how changes in energy prices can impact agricultural water demand in the Southeast.
The results from this study have implications for water supplies, water planning, and future agricultural water management in Tennessee and the southeastern United States. If corn prices follow FAPRI (2012) predictions, investment in corn irrigation will likely continue to expand into less water-intensive crops, such as cotton, common to Tennessee and other states in the southeastern region of the United States. Therefore, agricultural water use could continue to increase in the region. Policy makers may be interested in developing water policies to manage agricultural water use, such as creating incentives for crop producers to invest in efficient irrigation systems.
6. Conclusions
We evaluated the NPV of investing in a center-pivot irrigation system to produce corn in west Tennessee. We considered three field sizes and two energy sources and explored how the recent change in corn prices might have impacted the profitability of corn irrigation. Data used in this study came from a corn N-rate experiment located near Milan, Tennessee. We estimated yield response functions to N for nonirrigated and irrigated corn and used the estimated optimal yields and N fertilization rates for nonirrigated and irrigated corn to estimate the returns to irrigation. Little is known about the economics of irrigating corn in humid regions, but the results from this study will help extension personnel and producers in the southeastern United States determine if irrigating corn is profitable for various field sizes and energy sources.
Results from this study show that corn yield was increased and stabilized with irrigation in Tennessee. On average, irrigation increased corn yield by 66 bu./ac. in this study. Prior to 2006, the expected NPV for irrigating corn was negative across all field sizes and energy sources. However, post-2006, the expected NPV was positive for fields of 125 acres or larger that used either diesel or electric power. The probability of NPV being positive for fields of 125 acres or larger, which used either diesel or electric power, ranged between 3% and 31% for prices prevailing before 2006 and increased to between 87% and 100% for prices prevailing from 2006 to 2013. The expected NPV for using electric power was higher than for diesel power for all fields of 125 acres or larger. This result likely explains why irrigation investment has increased in Tennessee recently. If the price of corn follows FAPRI's (2012) projections in Tennessee and other humid regions of the United States, producers will likely continue investing in irrigation systems for corn production. However, our findings also suggest that corn prices will need to stay high for extended periods of time for irrigated production to remain profitable after investment in center-pivot irrigation under Tennessee growing conditions. Thus, investment in center-pivot irrigation may be a risky proposition for Tennessee producers if corn prices do not remain high.









