1. Introduction
Mexico is a major producer of both poultry and corn. Over the past decade, Mexico has also become the largest destination for exports of U.S. broiler meat and corn. In 2015 and 2016, Mexico accounted for almost 22% of U.S. broiler meat exports and about 28% of U.S. corn exports, representing more than $550 million in U.S. broiler exports and $2.3 billion in U.S. corn exports. Mexico’s production of corn consists primarily of white corn, which is used in tortillas, corn flour, and other products for human consumption (U.S. Department of Agriculture, Foreign Agriculture Service [USDA-FAS], 2000–2015). In contrast, Mexico’s chicken and pork industries use yellow corn, which is mostly imported from the United States, to grow out or finish animals.
Soybeans and soymeal are also imported from the United States. From 2010 to 2014, these imports averaged $2.5 billion a year and $660 million a year, respectively. Unlike the United States, Mexico uses a significant amount of sorghum as animal feed. Despite having a robust sorghum industry within Mexico, on average from 2010 to 2014, Mexico imported $750 million worth of sorghum from the United States. Most of Mexico’s feed imports were used in the growing poultry and hog industries.
U.S. exports of broiler meat and animal feed to Mexico grew considerably following the implementation of the North America Free Trade Agreement (NAFTA; see Table 1). Mexico’s consumption of chicken products rose from 1.7 million tons in 1997 to more than 4.1 million tons in 2016, while Mexico’s production of broiler meat rose from 1.5 to 3.3 million tons. Over this period, broiler meat imports rose from 160 to 820 thousand tons per year, most of which was imported from the United States.Footnote 1 Similarly, from 1996 to 2016, Mexico’s corn production rose from 19 million tons to 25 million tons a year, as corn imports from the United States grew from 3.1 million tons to 13.3 million tons.
Recently, several issues have surfaced that could influence U.S./Mexican trade in chicken and feed products. In 2015, avian influenza (AI) broke out in the turkey and chicken industries across the midwestern region of the United States. Migratory bird flocks from Asia were the most likely sources of contamination. In response to the AI outbreak, 34 countries discontinued imports of U.S. poultry products from various regions of the United States. In early 2017, another strain of AI (H7N9) was detected in Tennessee but was quickly contained. If another major outbreak of AI in the United States occurs, Mexico’s imports of U.S. poultry products could be limited or possibly eliminated.
A second factor is the uncertainty over Mexican and U.S. trade policies. A change in trade policy between the two countries could lead Mexican food importers to diversify their source of broiler meat and corn imports. Related to this is the rising consumption of meat products, which has provided an impetus for Mexico’s chicken industry to expand, modernize, and grow more of its own yellow corn.
A third issue that could disrupt U.S./Mexican trade of chicken products is Brazil’s growing role as a poultry exporter. Although Mexican imports of Brazilian corn have remained small, Mexican imports of Brazilian chicken meat have grown significantly in recent years. Improvements in Brazil’s roads and ports may soon allow Brazil to export agricultural products from northeastern regions of the country, potentially reducing the cost of shipping to the Mexican markets (Allen and Valdez, Reference Allen and Valdez2016).
Any of these changes could influence U.S. exports of broiler meat and feed products to Mexico. To measure possible impacts requires one to identify and quantify the factors that determine Mexico’s demand for U.S. broiler meat. In addition, it requires one to quantify the relationship between Mexico’s own chicken production, its feed use, and imports of feed grains.
This article evaluates the impacts of Mexican policy and market changes on imports of U.S. broiler meat and U.S. feed products. Two sets of demand models are estimated. First, a model of Mexico’s demand for broiler meat is estimated, which includes differentiating demand by its source. Second, a system of input demand equations, derived from a Mexican cost function for chicken production, is estimated. Imported feed demand equations are contained in the input demands. A price/marginal cost markup equation for chicken production is estimated as well. Parameters from this equation are used to connect the two sets of demand equations (broiler meat demand and input demands). Factors that influence Mexico’s purchases of domestic broiler meat are related to imports of U.S. feed products, which allows us to calculate how Mexico’s policy decisions affect exports of U.S. broiler meat and feed products to Mexico.
The next section briefly discusses output and input trade. This is followed by a discussion of Mexico’s demand for broiler meat, including specification of an Almost Ideal Demand System (AIDS) model. A subsequent section sets up feed demand equations by specifying the cost and marginal cost function for Mexican chicken production. Afterward an empirical section reports estimated buyer demand models, input demand models, and simulated impacts arising from changes in Mexican policy and other factors. A conclusions section sums up our results.
2. Output trade and input trade
Theoretically, the benefits of trade can be obtained by exchanging either outputs or inputs (Mundell, Reference Mundell1957). In Mundell’s (Reference Mundell1957) two-sector, two-factor, two-country model, trade in inputs substitutes for trade in outputs. Using a similar two-by-two-by-two model, but altering the reasons for trade, Markusen (Reference Markusen1983) showed that output and input trade can be complements. Markusen showed that if countries have different production technology or preferences, or if governments provide input subsidies to farmers, and if there are no constant returns to scale in production, movements toward input price equalization will not automatically occur when only outputs are traded between two sectors and two factors in a two-country model (Mundell, Reference Mundell1957). Rather, the level of both input trade and output trade must increase for output prices to equalize, while both countries’ input prices also move toward equality. Increases in output trade can increase input trade and vice versa. Later studies (Markusen, Reference Markusen1997; Samuelson, Reference Samuelson2001; Markusen, Rutherford, and Tarr, Reference Markusen, Rutherford and Tarr2005) continued to claim that trade in outputs and inputs or intermediate goods can complement each other.
Typically, countries have multiple trading partners, each having many economic sectors where a large number of inputs are exchanged, some mobile across sectors and others specific to a sector. Given these real-world complexities, trade outcomes may not always adhere to the predictions of simple economic theory. It is particularly difficult to capture the fundamentals inherent in Mexican-U.S. trade, which can involve two-way trade of multiple levels of intermediate goods (Baldwin and Lopez-Gonzalez, Reference Baldwin and Lopez-Gonzalez2015).
Although economists agree that output and input trade produce similar effects over the long run, the effects of input and output trade are not necessarily equivalent in the short run. For example, if Mexico were to suddenly import all of its broiler meat (an output or intermediate good) from the United States, chicken producers in the United States would immediately benefit. U.S. feed producers may benefit later as demand for chicken feed within the United States increases. The point is that in a complex economy with many sectors, even if the benefits of output and input trade were approximately equal, the gains from either form of trade would be distributed differently across the agricultural sector and regions of the United States.
In any case, economic theory could be used to argue that Mexican imports of feed would shrink if Mexico were to import more broilers (Mundell, Reference Mundell1957). Yet theory could be used to argue the opposite—that an increase in Mexico’s broiler meat imports would increase Mexico’s imports of feed products, if there are country differences in production technology, if there are input subsidies in either country, or if consumers’ preferences are different (Markusen, Reference Markusen1983). Therefore, empirical analysis is required to determine how Mexico broiler imports influence imports of feed products and how U.S. agriculture might be affected by changing trade between Mexico and the United States. To empirically explore these relationships, we first start with Mexico’s demand for broiler meat.
3. Mexico’s demand for chicken meat
Rising incomes and rapid urbanization in Mexico contributed to a more than 100% increase in chicken meat sales from 1997 to 2016. The bulk of these sales, between 80% and 90%, came from chickens grown in Mexico. Imports from Brazil and the United States represent the remaining purchases of chicken meat, the U.S. accounting for more than 95% of the imports.
U.S. exports consist primarily of leg quarters and mechanically deboned chicken meat, whereas all cuts from birds are produced in Mexico (Hayes, Reference Hayes2012; USDA-FAS, 2015). Market participants claim that domestic Mexican broiler meat is fresher, comes from smaller chickens with identifiable yellow skin, is cut differently, and is easily distinguished from imported chicken. A wide variety of market participants (retailers, processors, consumers, producers, and wholesalers) determine which type of broiler meat to purchase, but each market participant faces a similar choice.
Beginning with Burgess (Reference Burgess1974), a number of studies have portrayed imports as intermediate goods (Berns, Johnson, and Yi, Reference Berns, Johnson and Yi2011). Our analysis uses a single cost minimizing framework (Burgess, Reference Burgess1974; Lee, Nicita, and Olarreaga, Reference Lee, Nicita and Olarreaga2008) to portray Mexican buyers’ choice of imported or domestic chicken products, a decision that can be depicted as follows:
where Yim,i (i = 1, 2) represents broiler meat imports from the United States and Brazil, respectively. Ydm represents Mexico’s domestic chicken production, and pim represents the prices of imported chicken. Cu(1, w) is a measure of per unit production costs of broiler meat, which is a function of a vector of input prices w. In Mexico, chicken producers’ major inputs are feed grains. F(Yim, 1, Yim, 2,Ydm) is a function that translates imported and domestic chicken products into the desired level of production YCK.
The choice problem in equation Eq. (1) represents a demand decision faced by buyers of broiler meat. For exposition purposes, the domestic price is replaced by per unit costs. Assuming constant returns to scale per unit costs (average costs) equal marginal cost allows us to substitute the marginal cost of broiler meat production for Mexico’s price of broiler meat. The substitution between marginal cost and price is meant to emphasize the role imported feeds play in determining Mexico’s broiler meat prices.
The constraint in equation (1) ensures that the desired level of the chicken product is attained. A buyer decision can be used to obtain the demand for Mexico’s imports and domestic broiler meat:
In a later section, we relax the constant returns to scale assumption and allow for price markups to exceed marginal cost.
The previous demand equations represent Mexico’s consumption of chicken meat from three sources: Brazil, the United States, and the domestic market. These equations are general enough to represent purchasing decisions for consumers, wholesalers, and processors. We do not identify the stage at which the decision between purchases of imports and domestic chicken is made. That is, somewhere in the marketing chain, there are buyers that must make the decision between importing foreign broiler meat or purchasing domestic broiler meat.
3.1. Specifying demand equations
To estimate demand, we assume that Mexico’s buyers practice multiple stage budgeting (Deaton and Muellbauer, Reference Deaton and Muellbauer1980). We first estimate Mexican demand for the sum of broiler meat from all sources. This represents an upper stage demand equation, which is specified as follows:
where Pchk, Pbf, and Prk are the Mexican prices of chicken, beef, and pork, respectively. GNP is the Mexican gross national product, which serves as a combined income and population variable. The final variable is the square root of the trend variable that is used to capture the growth in broiler meat demand arising from factors such as urbanization. To represent the lower stage demand, expenditure share equations for U.S., Brazilian, and Mexican chicken meat are specified as an AIDS model. Share equations are
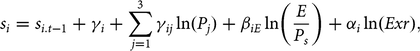 $${s_i} = {s_{i.t- 1}} + {\gamma_i} + \sum\limits_{\,j = 1}^3 {{\gamma_{ij}}} \,{\rm{ln}}({P_j}) + {\beta _{iE}}\,{\rm ln}\bigg({E \over {{P_s}}}\bigg) + {\alpha _i}\,{\rm ln}(Exr),$$(4)
$${s_i} = {s_{i.t- 1}} + {\gamma_i} + \sum\limits_{\,j = 1}^3 {{\gamma_{ij}}} \,{\rm{ln}}({P_j}) + {\beta _{iE}}\,{\rm ln}\bigg({E \over {{P_s}}}\bigg) + {\alpha _i}\,{\rm ln}(Exr),$$(4)
where si is the share of the demand for broiler meat from source i (sources: United States, Mexico, Brazil). si,t −1 is a one period lag share to capture habitual purchases by Mexico’s buyers. Pj is the price from each source, E is the total expenditures on broiler meat from all sources, Ps is the Stone price index consisting of share weighted average of source prices, and Exr is exchange rate. If the coefficient of exchange rate does not equal the sum of coefficients on prices, then the exchange rate should be used as a separate variable. This means that the buyers would react differently to an exchange rate change than price change.Footnote 2
Standard restrictions of homogeneity ![]() $\sum\nolimits_{j - 1}^3 {{\gamma _{ij}}} = 0$ and symmetry γij = γji are typically imposed on share equation parameters. When estimating a share based demand system of equations, one equation is dropped from the system because the expenditure shares in the system add to 1. Deaton and Muellbauer (Reference Deaton and Muellbauer1980) and a number of subsequent studies describe the AIDS model and method for calculating demand elasticities (i.e., Green and Alston, Reference Green and Alston1990).
$\sum\nolimits_{j - 1}^3 {{\gamma _{ij}}} = 0$ and symmetry γij = γji are typically imposed on share equation parameters. When estimating a share based demand system of equations, one equation is dropped from the system because the expenditure shares in the system add to 1. Deaton and Muellbauer (Reference Deaton and Muellbauer1980) and a number of subsequent studies describe the AIDS model and method for calculating demand elasticities (i.e., Green and Alston, Reference Green and Alston1990).
4. The demand for feed inputs
Mexico’s buyers, represented by the abovementioned demand system, influence Mexico’s output of broiler meat (and chickens), which in turn influences demand for feed products. This section derives the demand for feed products used in Mexico’s chicken production. A translog cost function (Ball and Chambers, Reference Ball and Chambers1982; Grisley and Gitu, Reference Grisley and Gitu1985) for Mexico’s chicken production is specified and used to derive input demand equations. Input demands for poultry production include feed equations that can be used (along with a price/marginal cost equation) to estimate the impact of changes in Mexico’s chicken production on imports of feed.
Mexico’s feed imports are used primarily to help supply its feed requirements for the domestic poultry and pork industry. A small amount of imported feed is used in the dairy industry and to a lesser degree in the beef industry. Because Mexico’s cattle consume a small amount of feed (Juarez, Reference Juarez2015), we include only chickens and pigs in the translog cost function. The swine output variable is used to sift out feed demand that is not attributable to the production of chickens.
USDA-FAS Global Agriculture Information Network (GAIN) publications (Hernandez and Hernandez, Reference Hernandez and Hernandez2015; Hernandez and Parrish, Reference Hernandez and Parrish2017) claim that feed represents approximately 65% to 72% of the cost of Mexico’s chicken production. The three major feeds in poultry and pig production are yellow corn (most of which is imported from the United States), sorghum, and soybean/soymeal (Hernandez and Parrish, Reference Hernandez and Parrish2017).Footnote 3 Subtracting U.S. corn imports from Mexico’s consumption of feed corn (USDA-FAS, 2016) shows that Mexico’s domestic corn accounts for a small but growing percent of total feed consumption. Mexico’s imports of corn are assumed to be an excess demand, and it is assumed that domestic production is fixed. The premise behind this statement is consistent with how most trade models treat imported products (see Bredahl, Meyers, and Collins, Reference Bredahl, Meyers and Collins1979; Lopez and Matschke, Reference Lopez and Matschke2006).
In the period prior to and immediately after the NAFTA agreement, the Mexican poultry industry experienced significant consolidation driven by large vertically integrated firms. According to Mayer (Reference Mayer2002), by 2002, 71% of poultry production was carried out on farms with more than 100,000 birds. The technology used in these production facilities is similar to that used in the United States. When estimating a translog cost function for the U.S. turkey industry, Grisley and Gitu (Reference Grisley and Gitu1985) included electricity, feed, and poults (baby chickens). Given the similarity in production technology, we also included prices representing these two inputs in our cost function. Our translog cost function was specified as
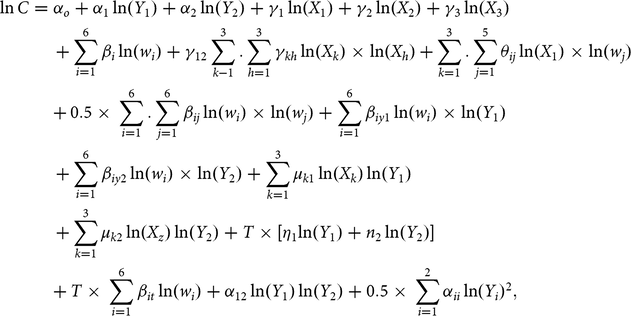 $$\eqalign{{\rm {ln}}\,C = {\alpha _o} + {\alpha _1}\ln \left( {{Y_1}} \right) + {\alpha _2}\ln \left( {{Y_2}} \right) + {\gamma _1}\ln \left( {{X_1}} \right) + {\gamma _2}\ln \left( {{X_2}} \right) + {\gamma _3}\ln \left( {{X_3}} \right) \cr + \mathop \sum \limits_{i = 1}^6 {\beta _ i}\ln \left( {{w_i}} \right) + {\gamma _{12}}\mathop \sum \limits_{k - 1}^3 .\mathop \sum \limits_{h = 1}^3 {\gamma _{kh}}\ln \left( {{X_k}} \right) \times {\rm {ln}}\left( {{X_h}} \right)\mathop +\sum \limits_{k = 1}^3 .\mathop \sum \limits_{j = 1}^5 {\theta _{ij}}\ln \left( {{X_1}} \right) \times {\rm {ln}}({w_j}) \cr + \,0.5 \times \mathop \sum \limits_{i = 1}^6 .\mathop \sum \limits_{j = 1}^6 {\beta _{ij}}\ln \left( {{w_i}} \right) \times {\rm {ln}}({w_j}) + \mathop \sum \limits_{i = 1}^6 {\beta _{iy1}}\ln \left( {{w_i}} \right) \times {\rm {ln}}({Y_1}) \cr + \mathop \sum \limits_{i = 1}^6 {\beta _{iy2}}\ln \left( {{w_i}} \right) \times {\rm {ln}}({Y_2}) + \mathop \sum \limits_{k = 1}^3 {\mu _{k1}}\,{\rm {ln}}({X_k})\,{\rm {ln}}\left( {{Y_1}} \right) \cr + \mathop \sum \limits_{k = 1}^3 {\mu _{k2}}\,{\rm {ln}}({X_z})\,{\rm {ln}}\left( {{Y_2}} \right) + T \times \left[ {{\eta _1}{\rm {ln}}\left( {{Y_1}} \right) + {n_2}\,{\rm {ln}}\left( {{Y_2}} \right)} \right] \cr + \,T \times \mathop \sum \limits_{i = 1}^6 {\beta _{it}}\ln \left( {{w_i}} \right) + {\alpha _{12}}\ln \left( {{Y_1}} \right)\ln \left( {{Y_2}} \right) + 0.5 \times \mathop \sum \limits_{i = 1}^2 {\alpha _{ii}}\ln {\left( {{Y_i}} \right)^2},}$$(5)
$$\eqalign{{\rm {ln}}\,C = {\alpha _o} + {\alpha _1}\ln \left( {{Y_1}} \right) + {\alpha _2}\ln \left( {{Y_2}} \right) + {\gamma _1}\ln \left( {{X_1}} \right) + {\gamma _2}\ln \left( {{X_2}} \right) + {\gamma _3}\ln \left( {{X_3}} \right) \cr + \mathop \sum \limits_{i = 1}^6 {\beta _ i}\ln \left( {{w_i}} \right) + {\gamma _{12}}\mathop \sum \limits_{k - 1}^3 .\mathop \sum \limits_{h = 1}^3 {\gamma _{kh}}\ln \left( {{X_k}} \right) \times {\rm {ln}}\left( {{X_h}} \right)\mathop +\sum \limits_{k = 1}^3 .\mathop \sum \limits_{j = 1}^5 {\theta _{ij}}\ln \left( {{X_1}} \right) \times {\rm {ln}}({w_j}) \cr + \,0.5 \times \mathop \sum \limits_{i = 1}^6 .\mathop \sum \limits_{j = 1}^6 {\beta _{ij}}\ln \left( {{w_i}} \right) \times {\rm {ln}}({w_j}) + \mathop \sum \limits_{i = 1}^6 {\beta _{iy1}}\ln \left( {{w_i}} \right) \times {\rm {ln}}({Y_1}) \cr + \mathop \sum \limits_{i = 1}^6 {\beta _{iy2}}\ln \left( {{w_i}} \right) \times {\rm {ln}}({Y_2}) + \mathop \sum \limits_{k = 1}^3 {\mu _{k1}}\,{\rm {ln}}({X_k})\,{\rm {ln}}\left( {{Y_1}} \right) \cr + \mathop \sum \limits_{k = 1}^3 {\mu _{k2}}\,{\rm {ln}}({X_z})\,{\rm {ln}}\left( {{Y_2}} \right) + T \times \left[ {{\eta _1}{\rm {ln}}\left( {{Y_1}} \right) + {n_2}\,{\rm {ln}}\left( {{Y_2}} \right)} \right] \cr + \,T \times \mathop \sum \limits_{i = 1}^6 {\beta _{it}}\ln \left( {{w_i}} \right) + {\alpha _{12}}\ln \left( {{Y_1}} \right)\ln \left( {{Y_2}} \right) + 0.5 \times \mathop \sum \limits_{i = 1}^2 {\alpha _{ii}}\ln {\left( {{Y_i}} \right)^2},}$$(5)
where Y 1 is the number of chickens in Mexico (in a particular month), Y 2 is the number of pigs, X 1 is Mexico’s domestic production of sorghum (represented as fixed input by the feed industry), X 2 is Mexico’s domestic production of soybeans, X 3 is Mexican production of feed corn as well as imports from sources other than the United States, w 1 is the price of eggs, w 2 is the price of imported yellow corn, w 3 is the price of import sorghum, w 4 is the price of imported soybeans, w 5 is the price of imported soymeal, w6 is the price (subsidized) of electricity, and T is a time variable meant to capture changes in production technology.
Input demands in the form of cost shares can be derived from a translog cost function (Ball and Chambers, Reference Ball and Chambers1982; Grisley and Gitu, Reference Grisley and Gitu1985). Using Shepard’s lemma, input share equations are
 $${{\partial {\rm{ln}}C} \over {\partial {\rm{ln}}{w_i}}} = {s_i} = {\beta _i} + \mathop\sum \limits_{j = 1}^5 {\beta _{ij}}\ln\left( {{w_i}} \right) + {\beta _{iy1}}{\rm{ln}}({Y_1}) + {\beta _{iy2}}\ln\left( {{Y_2}} \right) + \mathop\sum \limits_{k = 1}^3 {\theta _{ik}}\,{\rm{ln}}\,({X_k})$$(6)
$${{\partial {\rm{ln}}C} \over {\partial {\rm{ln}}{w_i}}} = {s_i} = {\beta _i} + \mathop\sum \limits_{j = 1}^5 {\beta _{ij}}\ln\left( {{w_i}} \right) + {\beta _{iy1}}{\rm{ln}}({Y_1}) + {\beta _{iy2}}\ln\left( {{Y_2}} \right) + \mathop\sum \limits_{k = 1}^3 {\theta _{ik}}\,{\rm{ln}}\,({X_k})$$(6)
for i = yellow corn, sorghum, soybeans, soymeal, hatching eggs. Price elasticities for feed inputs and hatching eggs can be calculated from the estimated system of share equations.
5. Relating Mexico’s chicken output to demand for feed grains
The cost function parameters μ k1, (k = 1,2,3), α 1, α 11, α 12 are not included in the input share equations. In the Appendix, we show that when the production technology is not constant returns to scale, estimates of these parameters are needed to measure the impact of chicken output (Y 1) on imports of U.S. feed products. This is a critical problem because it is the relationship between inputs and chicken output that links Mexico’s demand for domestic broiler meat with demand for feed imports. One way to obtain these parameters is to directly estimate the entire cost function. This can be difficult when there are a large number of variables, which could lead to severe multicollinearity problems.
However, the missing parameters are also contained in a marginal cost equation, which we estimate along with the input share equations. Recall that in equation (2), the marginal production cost (of Mexican chicken) was used in place of the domestic (wholesale) price. This comes from the price/marginal cost relationship:
If markets are not perfectly competitive (Tirole, Reference Tirole1988), output is produced to the point where
CV represents a measure of conjectural variations and is positive.Footnote 4 The price flexibility term ∂pdm/∂Ydm is negative. We refer to equation (8) as the price markup equation.
There are many different ways to transform a price markup equation to make it more amenable to estimation (Bhuyan and Lopez, Reference Bhuyan and Lopez1997; Arnade, Pick, and Gopinath, Reference Arnade, Pick and Gopinath1998). The markup over marginal cost is represented as an additive term, which ensures the markup equation is linear in parameters. To specify the price equation with an additive markup term and remain compatible with the translog cost function, we multiplied the second term on the right-hand side in equation (8) by one (in brackets in equation 9a) to produce:
where AC is the average cost of production. Given the cost function in equation (6), the specification of the markup equation becomes
 $$\begin{align}{{P_{dm}} = {\alpha_1}AC + {\alpha _{11}}\,\ln({Y_1}) \times AC + {\alpha _{21}}\ln\left( {{Y_2}} \right) \times AC + \mathop\sum \limits_{i = 1}^4 {\beta _{iy1}}\,{\rm{ln}}\left( {{w_i}} \right) \times AC + \sum_{k = 1}^3 {\mu _{k1}}\,\ln({X_k}) \times AC + \theta \times cndx,}\end{align}$$(10)
$$\begin{align}{{P_{dm}} = {\alpha_1}AC + {\alpha _{11}}\,\ln({Y_1}) \times AC + {\alpha _{21}}\ln\left( {{Y_2}} \right) \times AC + \mathop\sum \limits_{i = 1}^4 {\beta _{iy1}}\,{\rm{ln}}\left( {{w_i}} \right) \times AC + \sum_{k = 1}^3 {\mu _{k1}}\,\ln({X_k}) \times AC + \theta \times cndx,}\end{align}$$(10)
where cndx is an index of industry competiveness and θ is a parameter to be estimated.
Although estimation of equation (10) can be of interest in its own right, our goal here is to use estimates of parameters, α 1, α 11, α 21, and μ k1 to calculate how Mexico’s output of chicken influences demand for feed inputs. This allows us to relate Mexico’s consumption of domestic broiler meat to Mexico’s chicken production by adjusting for dress weight and the number of layer chickens. Given this derived output, we then can determine changes in Mexico’s imports of feed grains and soybeans.
6. Empirical results
6.1. Data
Monthly data on Mexico’s imports of U.S. and Brazilian broiler meat are obtained from the Global Trade Atlas database (IHS Markit, 2016). Quantity and value data are used to calculate import unit price. Data on Mexico’s imports of chicken parts are obtained using the Harmonized System for classifying goods at the six-digit code system.
Mexico’s production and consumption of chicken are obtained from USDA-FAS (2016). Using U.S. carcass weight estimates, we assumed that dressed chicken equaled 70% of live weight chicken. Taking estimates of food loss, we assumed 10% of produced chickens were lost prior to consumption. Mexico’s domestic price of chickens is represented by chicken prices sold by the domestic company Bachoco (35% of Mexico’s broiler market) in Mexico City’s San Juan market (Secretaría de Economía, Mexico, 2015). To ensure that our findings are robust, we also estimated our model using the San Juan price of live chickens (whole bird).Footnote 5
The price of hatching eggs from Mexico’s Sistema Nacional de Informacion e Integracion de Mercados (Secretaría de Economía, Mexico, 2015) is based on eggs sold at the wholesale level in Mexico from 2000 to 2016. We adjusted this price by using the relationship between Mexico’s import unit values of consumer eggs (IHS Markit, 2016) and hatching eggs.Footnote 6 To compute the number of hatching eggs purchased by chicken producers, we lagged the number of chickens 3 months.Footnote 7 This does not account for eggs lost. We assume the loss remains constant, so that the variation in our egg quantity index captures the variation in eggs purchased.
Mexico’s subsidized electricity price (for agriculture) is obtained from the website of Mexico’s Secretaría de Energía (2016) and is included in the cost function. We did not have data to estimate poultry producers’ demand for electricity.
6.2. Estimating chicken demand
Using monthly data from 1997 to November 2015, the upper stage demand equation (3) is estimated first. The Mexican chicken price is represented by a share weighted average of chicken prices from the three sources: Brazil, Mexico, and the United States. Coefficients and T-statistics for each exogenous variable are reported in Table 2. The GNP variable and trend are highly significant. Cross-price elasticities for pork and beef are significant, positive, but small, suggesting that pork and beef are weak substitutes for chicken meat. The exchange rate variable is insignificant. We included lag shares, which came out highly significant, indicating that Mexican buyers tend to be habitual buyers.
Table 1. Value and quantity of U.S. exports to Mexico
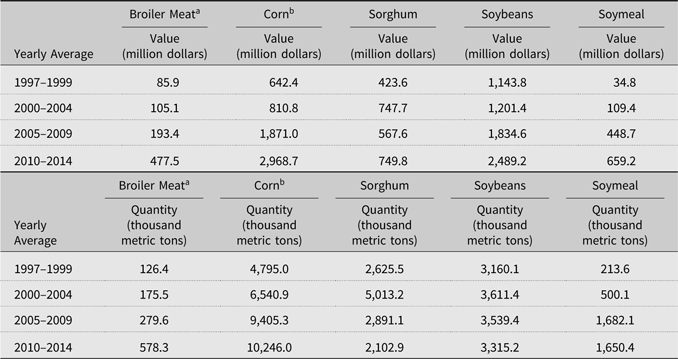
a Source: Global Trade Atlas (2016).
b Source: U.S. Department of Agriculture, Foreign Agriculture Service (2016).
Table 2. Upper stage Mexican demand for broiler meata
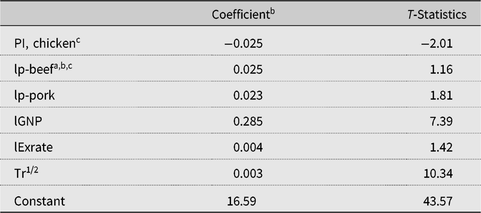
a The dependent variable is the log of total broiler meat purchased in Mexico each month.
b Exogenous variables are in logs; thus coefficient estimates equal elasticities.
c The price of chicken is a share weighted average of Mexican broiler meat, import unit values of U.S. broiler meat, and imported Brazilian broiler meat.
Notes: lExtrate, natural log of the exchange rate; lGNP, natural log of GNP; lp, natural log of price; Tr1/2, square root of trend variable.
Table 3 reports elasticities and Table 4 presents the parameter estimates from the lower stage AIDS model. We checked the AIDS model for robustness in several ways. First, we estimated the AIDS model in differences (Eales and Unnevehr, Reference Eales and Unnevehr1988). We also experimented with different prices for Mexican broiler meat. Tests are conducted to determine if a trend variable, an exchange rate variable, and lag shares variables belonged in the model.
Table 3. Lower stage demand AIDS (Almost Ideal Demand System) elasticities, chicken demand by source
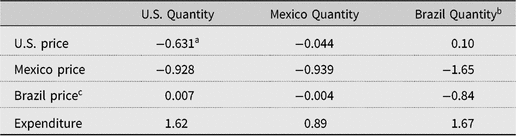
a A 10% increase in U.S. broiler meat prices would reduce imports of U.S. broiler meat by 6.3%.
b Coefficients for the Brazilian share equation were derived by taking the estimated coefficients from the above share equations and exploiting symmetry and homogeneity and adding up conditions. Brazilian elasticities were calculated using these coefficients.
c Elasticities calculated using formula (iii), of Green and Alston (Reference Green and Alston1990).
Table 4. AIDS (Almost Ideal Demand System) demand share equations: lower stage
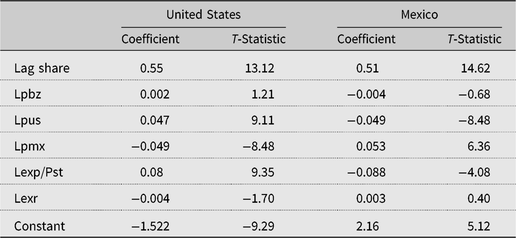
Notes: Lpbz, natural log of Brazilian price (broiler meat); Lexp/Pst, natural log of expenditures on Stone price index; Lexr, natural log of U.S.-Mexican exchange rate; Lpmx, natural log of Mexican price (broiler meat); Lpus, natural log of U.S. price (broiler meat).
In models without lag shares or an exchange rate variable, U.S. broiler meat came out as an inferior good, and Mexican and U.S. broiler meat as substitutes. However, for models that included an added exchange rate effect, a trend variable, or a lag share variable, U.S. broiler meat came out as a normal good, and Mexican and U.S. broiler meat as complements.Footnote 8
Exchange rate and lag share coefficients were significant, so we chose to incorporate these two variables into the model. In the model, Mexican demand for U.S. broiler meat is inelastic (approximately equal to −0.63), whereas the demand for Mexico’s own domestic meat is barely inelastic (−0.93). The difference in the two elasticities provides some indication that Mexican buyers distinguish between both types of broiler meat.Footnote 9 Findings show that Mexican domestic chicken and U.S. broiler meat are complements. The complementary relationship implies that lower prices of one country’s broiler meat increases demand for the other country’s broiler meat. This can be consistent with two-stage budgeting where expenditure on a particular category of products is predetermined. It also supports the claim made by some market analysts who say that Mexican stores use U.S. broiler meat as a loss leader.
Several other studies have found complementarity between imports of broiler meat and imports of white meat or between imports and domestic broiler meat (Mexico: Henneberry and Mutondo, Reference Henneberry and Mutondo2007; Japan and Korea: Mutondo, Henneberry, and Brorsen, Reference Mutondo, Henneberry and Brorsen2010; Mexico, mixed results: Lopez et al., Reference Lopez, Malaga, Chidmi, Belasco and Surles2012). Bett et al. (Reference Bett, Musyoka, Peters and Bokelmann2012) found broiler meat imports and domestic poultry meat were complements in Kenya. Davis and Dyck (Reference Davis and Dyck2015) found complementarity between Japan’s imports of U.S. leg quarters and imports of white meat from Thailand prior to 2004, but found these imports changed to substitutes after an avian flu outbreak in 2004.
In a comprehensive domestic demand study that disaggregated broiler cuts into many products, Goddard et al. (Reference Goddard, Shank, Panter, Nisson and Cash2007) found that Canadians treat drumsticks as complements with chicken breasts and found that chicken legs are complements to wings and thighs.
Another possible reason for complementarity (beyond the loss-leader explanation) is that preferences for broiler meat cuts vary within families. This would be particularly likely among multigenerational households commonly found in Mexico. Older family members are likely to prefer traditional domestic cuts of broiler meat, whereas younger members may prefer packaged imported meat. Whatever the case, this study cannot determine the driving force behind the observed complementarity among broiler meat cuts. However, the loss-leader explanation and existence of mixed generational households are both consistent with our econometric results.
6.3. Estimating input demands for Mexican chicken production
Using the specification expressed in equation (6), we estimated the demand for five variable inputs: imported yellow corn, U.S. soybeans, U.S. soymeal, U.S. sorghum, and hatching eggs. As noted earlier, Mexico’s chicken industry imports most of its yellow corn, soybeans, soymeal, and sorghum from the United States. Domestic sorghum and soybeans are treated as fixed inputs, as well as any feed corn not supplied by the United States. This implies that imports of feed represent an excess demand, which is the standard way to treat imports in the trade literature (Bredahl, Meyers, and Collins, Reference Bredahl, Meyers and Collins1979; Stockhammer, Onaran, and Ederer, Reference Stockhammer, Onaran and Ederer2009).
Our cost function has two output variables, the number of chickens in Mexico and the number of pigs. Both layers and broilers are included in the chicken numbers to account for feed use. When examining the impact of broiler demand on feed use, we account for the fact that broilers are a share (54% in 2015) of Mexico’s total chicken production.
Using monthly data from 1978 to 2015, a system of five cost share equations is jointly estimated along with the price markup equation. Although input cost shares add to one, with the addition of a price markup equation, the error terms in the six-equation system do not add to zero. Therefore, we did not drop an input share equation when estimating the system. The following symmetry and homogeneity restrictions on input prices are imposed: βij = βji and ∑βij = 0.Footnote 10 Cross equation equality restrictions are also imposed on parameters that are common to both input demand equations and the price markup equation. Estimated input demands and price markup equations are presented in Table 5.
Table 5. Input demand elasticitiesa
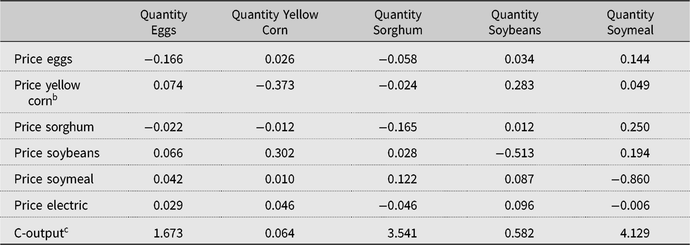
a Represents the change in demand for inputs used for chicken production in response to a change in the price or output.
b Feed inputs represent imported feed. Domestic sorghum, soybeans, feed corn, and feed corn imported from countries other than the U.S. are treated as fixed inputs.
c For example, a 10% increase in corn prices reduces demand for eggs by 3.73%. A 10% rise in Mexico’s chicken output increases demand for soybeans by 5.82%.
Note: C-output, chicken output.
The response of feed (input) demands with respect to a change in the level of chicken production in Mexico is key to our analysis. In elasticity form (see Appendix), this relationship is
The last term on the right-hand side in equation (11) denotes the economies of scale. While testing our estimated cost function for scale economies, we found that Mexican chicken production is nonhomothetic, so the second term on the right-hand side changes at every data point (Ball and Chambers, Reference Ball and Chambers1982). On average, the value of the scale elasticity, the second term on the right-hand side in equation (11), is 1.14, which suggests that at the average observed level of output, Mexico’s production technology is subject to decreasing returns to scale (or increasing costs). The elasticities of input demand with respect to a change in chicken output are presented in Table 6.
Table 6. Input demands Mexican poultry: share equations and price markup equation
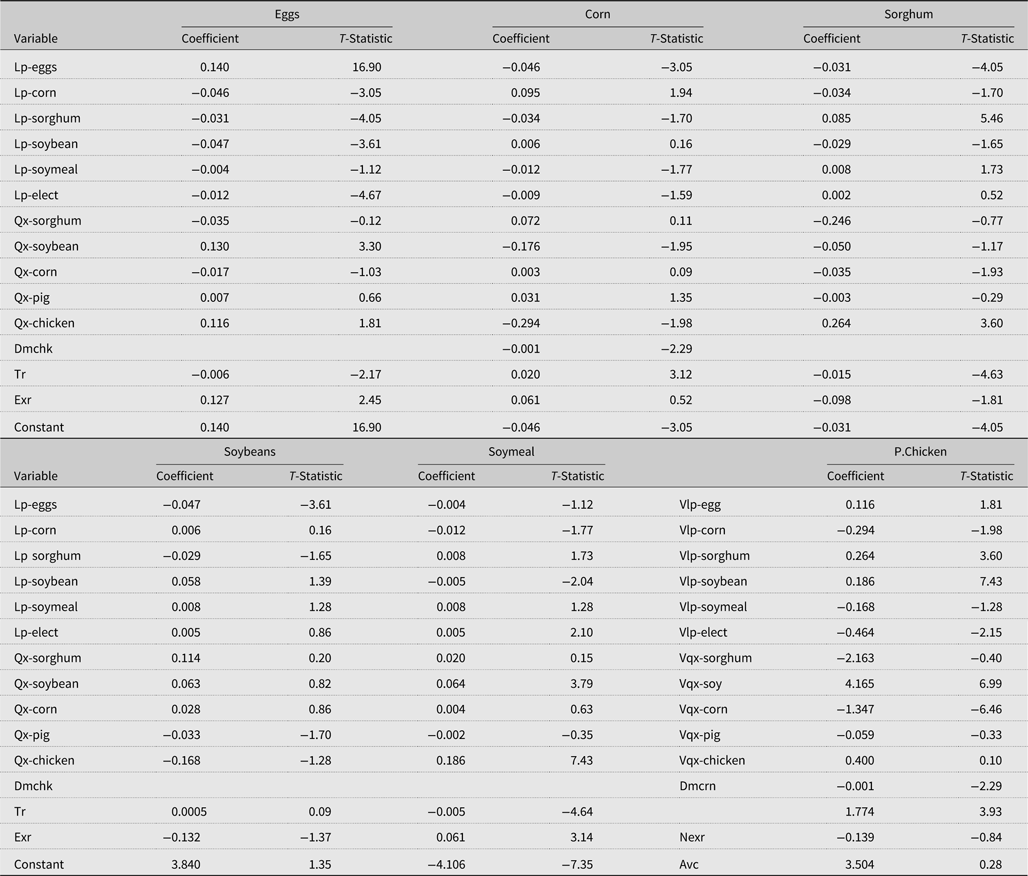
Notes: Avc, average cost of chicken production; Dmchk, dummy variable interated with chk (number of chickens) variable; Dmcrn, dummy variable interacted with crn (weighted log of corn price) variable; Exr, exchange rate; Lp, log price; Nexr, natural log of peso/dollar exchange rate; Qx, quantity production Mexico; Tr, time trend variable; Vlp, log price interacted with average cost; Vqx, production quantity interacted with average cost. P.Chicken is the price markup equation.
6.4. Impacts arising from changes in upper stage variables
The upper stage equation (Mexico’s total demand for broilers) and lower stage AIDS demand equations (demand by source of origin) are combined to calculate the impact of upper stage variables on imports of U.S., Mexican, and Brazilian broilers. Table 7 shows that a 5% change in GNP initially increases Mexico’s demand for all broiler meats by 2.9%. This, in turn, increases demand for U.S. chicken by 4.6% and raises consumption of domestic chicken by 2.6% and Brazilian chicken by 4.8%. Estimated cost function parameters indicate that a 2.6% increase in Mexican output increases imports of U.S. corn by 0.13%, sorghum by 7%, soybeans by 1.15%, and soymeal by 8.2%. However, the initial GNP impact is eventually tempered by a rise in the broiler meat price. A 2.6% increase in the quantity produced requires a 0.21% rise in the broiler meat price (calculated from the price markup equation) slightly reducing demand. Iterating this change between the price markup and demand equations shows that the demand for Mexico’s broiler meat rises only by 1.22% one year after the GNP change (compared with 2.6% rise in demand at impact). After 1 year, imports of feed are proportionally lower.
Table 7. Mexico’s economic variables and broiler meat demand by sourcea
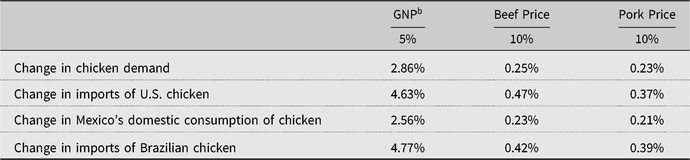
a Demand changes result from the interaction of the top level model and the second stage AIDS (Almost Ideal Demand System) equations.
b Symmetric changes in the demand result are attributable to a decline in GNP. Symmetry holds for all remaining tables also.
A 10% rise in Mexican beef prices will increase Mexico’s overall demand for broiler meat by only 0.25%. This, in turn, increases imports of U.S. broiler meat by less than 0.47%, domestic broilers by 0.23%, and Brazilian broilers by 0.42. A 10% rise in Mexican pork prices creates a similarly small increase in demand for broiler meat in Mexico.
6.5. The impact of Mexico’s import restrictions
Mexico could limit imports of U.S. broiler meat. This might occur, for example, if there are additional outbreaks of avian flu in the U.S. poultry industry or if Mexico and the U.S. alter their trade policy. Cross price elasticities from our demand model show that a rise in U.S. broiler meat price, stemming from a tariff, reduces not only demand for U.S. broiler meat but also Mexico’s demand for its own broiler meat.Footnote 11 There could be two possible ways Mexico could handle an outright ban on imports of U.S. broiler meat: Mexico could put in place policies to ensure that domestic production will cover the loss in broiler meat imports. This would be a complete import substitution policy. As a result of this policy, imports of feed products from the United States would significantly increase. On the other hand, Mexico could ban imports and allow the subsequent price effect of an import ban to determine the response of buyers and sellers. In this case, demand for feed products in the United States would decrease. Finally, Mexico could use a tariff to limit broiler meat imports. In this scenario, imports of feed products would decline. The point is that how Mexico chooses to limit broiler meat imports has a significant effect on what happens to imports for feed from the United States.
Column 1 of Table 8 displays the impact on demand for feed grains and domestic broiler meat if Mexico replaced all of the U.S. broiler imports with domestically produced meat. Over the last 24 months of the period covered by our model, Mexico imported approximately 22% of its chicken meat from the United States. The dressed weight of chicken is approximately 70% of production weight, and 54% of Mexican chickens are broilers. To make up for the loss in supply, Mexico’s producers would need to increase chicken output by 16.9%. This, in turn, would increase imports of U.S. feed corn by 1.1%; sorghum, 60.1%; soybeans, 9.88%; and soymeal, 70%. However, estimates from the price markup equation reveal that in order to obtain this rise in output, the price of domestically produced broiler meat would need to rise 2.6%
Table 8. Mexico’s input demand from U.S. broiler meat ban and tariffs
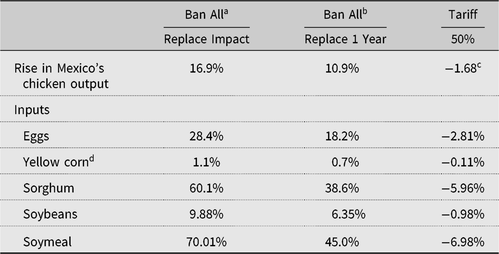
a A total import ban with replace increases Mexican production 16.9% output.
b Taking into account the effect of a ban on price, production only rises 10.9 after 1 year. That is, a higher price reduces demand, so Mexico does not completely replace U.S. imports.
c A 50% tariff causes Mexico to reduce its own production by 1.68% because U.S. broiler meat and Mexican broiler meat are complements.
d Corn, sorghum, soybeans, and soymeal refer to U.S. imports. For example, a 16.9% increase in Mexican chicken production would increase imports of U.S. corn by 1.1%.
At the new feed output and price level, imports of U.S. corn, sorghum, soybeans, and soymeal will rise by 0.7%, 38.6%, 6.36%, and 45.2%, respectively (not shown in tables). Given the average value of exports from 2010 to 2014 at current prices, annual corn exports would increase by approximately $20.8 million, sorghum by $289 million, soybeans by $158 million, and soymeal by $298 million. The lost income from broiler exports would be approximately $447 million annually. Added together, U.S. exports would increase by an additional $319 million. One explanation for the increase in U.S. export value is that Mexicans pay a higher price for U.S. feed than do chicken producers in the United States. For example, Mexican imported corn price is 77% higher, on average, than Illinois wholesale price (USDA, Economic Research Service, 2016). Another possible reason is that the United States could be more efficient in converting feed into pounds of broiler meat. More importantly, there would be an obvious transfer of revenue from one group of U.S. exporters, located heavily in southern states, to another group of exporters located primarily in the Midwest and West.
Another possibility is for Mexico to not replace the banned imports but instead allow the price effects of a ban to work itself through. The estimated price elasticity of U.S. broiler meat imports reveals that a complete ban is equivalent to a 158% rise in price of imported U.S. broiler meat. Note that a large increase in price is needed (often called the choke price) to reduce imports of U.S. broiler meat to zero. Mexico’s broiler meat is a complement, so a rise in the U.S. price reduces demand for Mexican broiler meat. Given the low value of the cross price elasticity, a sizable increase in price will only reduce purchases of domestic broiler meat 6.9% (not shown in tables). However, imports of Brazilian broiler meat rise 1.98%. Adjusting for dress weight and the number of layers in Mexico, chicken output falls. When considering additional price and quantity effects, domestic output falls 5.5%, and U.S. corn, sorghum, soybean, and soymeal imports fall 0.36%, 19%, 3.2%, and 22.8%, respectively.
The third column of Table 8 shows the impact of an increase in Mexican tariffs on American broiler meat when Mexico does not protect consumers from price increases. A tariff of 50% reduces demand for U.S. broiler meat by 31.6%. Given a low complementary elasticity between U.S. and Mexican broiler meat demand, Mexican broiler meat only declines by 2.2%. Adjusting for dress weight and the number of layers, chicken output in Mexico declines by 1.68%. This drop in output decreases imports of U.S. corn, sorghum, soybean, and soymeal by 0.11%, 5.96%, 0.98%, and 6.9%, respectively. In this scenario, U.S. broiler meat exports to Mexico decline by $150 million annually, and corn, sorghum, soybean, and soymeal exports to Mexico decline by $3.3 million, $44.64 million, $24 million, and $45.5 million, respectively.
The abovementioned simulations show that trade levels in feeds and broiler meat are complements. This arises from the complementarity of Mexico’s domestic demand for U.S. broiler meat and its own cuts of domestic broiler meat. Markusen (Reference Markusen1983, Reference Markusen1997) and Markusen, Rutherford, and Tarr (Reference Markusen, Rutherford and Tarr2005) have shown that if production technologies are different between countries or if inputs are subsidized or taxed in either country, then trade in outputs alone may not force input prices to move toward equalization. Because of this difference in input prices, input and output trade will continue to exist. The economies of Mexico and the United States have all of these elements to some degree.
7. Conclusion
Mexico is the largest importer of U.S. broiler meat and one of the largest importers of U.S. feed corn. However, the emergence of avian flu in the United States raises the possibility that Mexico could limit imports of U.S. broiler meat. This article explores the relationship between Mexico’s imports of broiler meat and animal feeds. Two demand systems for Mexico are estimated: a demand for broiler meat and a demand for feed used in the production of Mexican chickens.
Using both demand systems and a price markup equation, we explore several possible scenarios. In the first scenario, we assume imports of U.S. broiler meat are cut off and Mexico production completely replaces lost imports from the United States. In this scenario, imports of U.S. feed products would increase. In the second scenario, we assume imports of U.S. broiler meat are cut off and Mexico allows subsequent price changes to determine supply and demand for broiler meat. The third scenario assumes tariffs on broiler meat are imposed. In the second and third scenarios, Mexico’s imports of U.S. animal feeds will fall. This result is consistent with our empirical finding that Mexico’s buyers treat domestic broiler meat and U.S. broiler meat as complements.
It should be emphasized that the findings in this article are not to be viewed as a final statement on the issue of Mexico’s broiler meat imports. Future research could use methods similar ours and focus exclusively on changes in trade policies. Simulation scenarios analyzed in this study could be reversed. Researchers could start with restrictions on various feed products and evaluate how these restrictions could influence imports of broiler meat. Another item to explore in detail is the effect of Brazil’s exports on broiler meat and feed products to Mexico. Currently, Brazil’s share of the Mexican broiler meat market is small, but it could grow significantly in the future.
Funding
The findings and conclusions in this preliminary publication have not been formally disseminated by the U.S. Department of Agriculture and should not be construed to represent any agency determination or policy. This research was supported by the intramural research program of the U.S. Department of Agriculture, Economic Research Service. We would like to thank Jeff Gillespie, Sean Ramos, and Steven Zahniser for helpful advice in carrying out this research.
Appendix
To measure how changes in Mexico’s output influence feed demand, we write the log of the cost share for feed input i as follows:
Solving for the ith input produces
Assuming input prices are exogenous, the impact of chicken output on the demand for the ith input is
In a single output cost function, the last term on the right-hand side represents the elasticity of scale. To measure the impact of Mexico’s chicken output on the demand for feed grains requires estimation of parameters that are not contained in the input demand equation. That is, using our cost function (allowing chicken = Y 1), the scale elasticity, the last term in equation (A3), is
The β iy1 parameters in equation (A4) can be obtained by estimating input share equations. However, parameters μk 1, α 1, α 21 are not represented in the input share equations. One way to obtain these remaining parameters is to estimate the cost function directly, which can be a difficult undertaking. The cost function contains a large number of variables, which could create severe multicollinearity problems, particularly among the many interaction terms. We estimate a price/marginal cost markup equation to obtain these parameters.










