Hostname: page-component-7bb8b95d7b-lvwk9 Total loading time: 0 Render date: 2024-09-20T21:34:36.004Z Has data issue: false hasContentIssue false
  • English
  • Français

On Hamiltonian Averaging Theories and Resonance

Published online by Cambridge University Press:  12 April 2016

S. Ferraz-Mello
S. Ferraz-Mello*
Affiliation:
Institute Astronômico e Geofísico, Universidade de São PauloSão Paulo, Brasil

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article, we review the construction of Hamiltonian perturbation theories with emphasis on Hori’s theory and its extension to the case of dynamical systems with several degrees of freedom and one resonant critical angle. The essential modification is the comparison of the series terms according to the degree of homogeneity in both 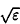and a parameter which measures the distance from the exact resonance, instead of just .

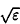Type
Dynamics and Astrometry: Present and Future
Information
International Astronomical Union Colloquium , Volume 165: Dynamics and Astrometry of Natural and Artificial Celestial Bodies , 1997 , pp. 39 - 50
Copyright
Copyright © Kluwer 1997

References

Bohlin, K.: 1888, “Über eine neue Annäherungsmetode in der Störungstheorie”, Bihang Svenska Vet.-Akad. 14 Afd. I No.5, 1–26.Google Scholar
Brouwer, D.: 1959, “Solution of the problem of artificial satellite theory without drag”, Astron. J. 64, 378–397.CrossRefGoogle Scholar
Brouwer, D. and Clemence, G.M.: 1961, Methods of Celestial Mechanics, Academic Press, New York.Google Scholar
Campbell, J.A. and Jefferys, W.H.: 1970, “Equivalence of the perturbation theories of Hori and Deprit”, Celest. Mech. 2, 467–473.Google Scholar
Carathéodory, C.: 1965, Calculus of Variations and Partial Differential Equations of the First Order, Holden-Day, San Francisco.Google Scholar
Deprit, A.: 1969, “Canonical transformation depending on a small parameter”, Celest. Mech. 1, 12–30.Google Scholar
Ferraz-Mello, S.: 1990, “Averaging Hamiltonian systems”, in: Modern Methods in Celestial Mechanics (Benest, D., Froeschlé, Cl., eds), Ed. Frontières, pp.151–211. Google Scholar
Ferraz-Mello, S.: 1997, Hamiltonian Averaging Theories and Resonance in Celestial Mechanics, to be published.Google Scholar
Garfinkel, B., Jupp, A. and Williams, C.: 1971, “A recursive Von Zeipel algorithm for the ideal resonance problem”, Astron. J. 76, 157.CrossRefGoogle Scholar
Gröbner, W.: 1960, Die Lie Reihen und ihre Anwendungen, Deutsche Verl. Wiss., Berlin.Google Scholar
Hori, G.-I.: 1966, “Theory of general perturbations with unspecified canonical variables”, Publ. Astron. Soc. Japan, 18, 287–296.Google Scholar
Jupp, A.: 1970, “On the ideal resonance problem - II”, Mon. Not. Roy. Astron. Soc. 148, 197–210.Google Scholar
Jupp, A.: 1982, “A comparison of the Brouwer-Von Zeipel and Brouwer-Lie series methods in resonant systems”, Celest. Mech. 26, 413–422.CrossRefGoogle Scholar
Jupp, A.: 1992, “Chapter XIX - Bohlin Methods”, Not. Scient. Techn. Bur. Longit. No. S 036.Google Scholar
Mersman, W.A.: 1970, “A new algorithm for the Lie transforms” Celest. Mech. 3, 81–89.CrossRefGoogle Scholar
Poincaré, H.: 1893, Les Méthodes Nouvelles de la Mécanique Celeste, Gauthier-Villars, Paris, Vol. II.Google Scholar
Sérsic, J.L.: 1956, Aplicaciones de un Certo Tipo de Transformaciones Canónicas a la Mecánica Celeste, Dr. Thesis, Univ. Nac. La Plata, (repr. Serie Astronomica, Obs. Astron. Univ. La Plata 35, 1969).Google Scholar
Sessin, W.: 1986, “A theory of integration for the extended Delaunay method”, Celest. Mech. 39, 173–180.Google Scholar
Von Zeipel, H.: 1916, “Recherches sur le mouvement des petites planètes”, Arkiv. Mat. Astron. Fysik, 11–13.Google Scholar