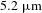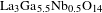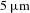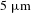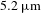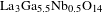1 Introduction
Ultrafast light fields enable studies of ultrafast processes in physics, chemistry and biology at the femtosecond scale[Reference Sibbett, Lagatsky and Brown1]. An intense ultrafast laser field can even ionize the electrons from the parent atom, which will be further accelerated in the light field and finally recombine with the atom. Such a strong-field process can emit high harmonics of the drive laser[Reference Zhou, Peatross, Murnane, Kapteyn and Christov2]. Due to the coherent nature of the process, high harmonic generation (HHG) can convert a femtosecond pulse to previously inaccessible attosecond pulses and thereby open a door to attosecond science[Reference Krausz and Ivanov3]. In addition, an intense ultrafast light field can accelerate an electron or protons with an acceleration gradient that is three orders of magnitude higher than that of a conventional microwave accelerator and holds promise for constructing table-top laser accelerators[Reference Tajima and Dawson4].
One core parameter in strong-field physics is the electron quiver energy,
![]() $E_{q}$
, which depends on the laser intensity
$E_{q}$
, which depends on the laser intensity
![]() $I$
and wavelength
$I$
and wavelength
![]() $\unicode[STIX]{x1D706}$
according to
$\unicode[STIX]{x1D706}$
according to
![]() $E_{q}\propto I\unicode[STIX]{x1D706}^{2}$
[Reference Perry and Mourou5]. To increase
$E_{q}\propto I\unicode[STIX]{x1D706}^{2}$
[Reference Perry and Mourou5]. To increase
![]() $E_{q}$
, a high-intensity laser is obviously necessary. With the aid of chirped-pulse amplification (CPA), near-infrared (IR) ultrafast lasers with peak powers up to several PW have been available, which can reach an extreme intensity of
$E_{q}$
, a high-intensity laser is obviously necessary. With the aid of chirped-pulse amplification (CPA), near-infrared (IR) ultrafast lasers with peak powers up to several PW have been available, which can reach an extreme intensity of
![]() ${\sim}10^{21}~\text{W}/\text{cm}^{2}$
and promote laser–matter interactions into the relativistic regime[Reference Danson, Haefner, Bromage, Butcher, Chanteloup, Chowdhury, Galvanauskas, Gizzi, Hein, Hillier, Hopps, Kato, Khazanov, Kodama, Korn, Li, Li, Limpert, Ma, Nam, Neely, Papadopoulos, Penman, Qian, Rocca, Shaykin, Siders, Spindloe, Szatmári, Trines, Zhu, Zhu and Zuegel6]. However, it becomes increasingly difficult to further enhance the laser peak power, although hundred-petawatt laser facilities are planned. With a fixed laser intensity, an increase in the laser wavelength can be regarded as a new route to scale up
${\sim}10^{21}~\text{W}/\text{cm}^{2}$
and promote laser–matter interactions into the relativistic regime[Reference Danson, Haefner, Bromage, Butcher, Chanteloup, Chowdhury, Galvanauskas, Gizzi, Hein, Hillier, Hopps, Kato, Khazanov, Kodama, Korn, Li, Li, Limpert, Ma, Nam, Neely, Papadopoulos, Penman, Qian, Rocca, Shaykin, Siders, Spindloe, Szatmári, Trines, Zhu, Zhu and Zuegel6]. However, it becomes increasingly difficult to further enhance the laser peak power, although hundred-petawatt laser facilities are planned. With a fixed laser intensity, an increase in the laser wavelength can be regarded as a new route to scale up
![]() $E_{q}$
. To achieve a certain value of
$E_{q}$
. To achieve a certain value of
![]() $E_{q}$
, the use of a long-wavelength drive laser can lower the requirement of laser intensity. For example, both a
$E_{q}$
, the use of a long-wavelength drive laser can lower the requirement of laser intensity. For example, both a
![]() $0.8~\unicode[STIX]{x03BC}\text{m}$
laser with
$0.8~\unicode[STIX]{x03BC}\text{m}$
laser with
![]() $I=9\times 10^{17}~\text{W}/\text{cm}^{2}$
[Reference Nakamura, Iwashita, Noda, Shirai, Tongu, Fukumi, Kado, Yogo, Mori, Orimo, Ogura, Sagisaka, Nishiuchi, Hayashi, Li, Daido and Wada7] and a
$I=9\times 10^{17}~\text{W}/\text{cm}^{2}$
[Reference Nakamura, Iwashita, Noda, Shirai, Tongu, Fukumi, Kado, Yogo, Mori, Orimo, Ogura, Sagisaka, Nishiuchi, Hayashi, Li, Daido and Wada7] and a
![]() $10.6~\unicode[STIX]{x03BC}\text{m}$
laser with
$10.6~\unicode[STIX]{x03BC}\text{m}$
laser with
![]() $I=10^{16}~\text{W}/\text{cm}^{2}$
[Reference Pogorelsky, Yakimenko, Polyanskiy, Shkolnikov, Ispiryan, Neely, McKenna, Carroll, Najmudin and Willingale8] have accelerated protons to a similar energy of
$I=10^{16}~\text{W}/\text{cm}^{2}$
[Reference Pogorelsky, Yakimenko, Polyanskiy, Shkolnikov, Ispiryan, Neely, McKenna, Carroll, Najmudin and Willingale8] have accelerated protons to a similar energy of
![]() ${\sim}1~\text{MeV}$
. HHG with a mid-IR driver can produce water-window X-rays and hard X-rays because the cutoff energy of the HHG process scales with
${\sim}1~\text{MeV}$
. HHG with a mid-IR driver can produce water-window X-rays and hard X-rays because the cutoff energy of the HHG process scales with
![]() $\unicode[STIX]{x1D706}^{2}$
[Reference Popmintchev, Chen, Popmintchev, Arpin, Brown, Ališauskas, Andriukaitis, Balčiunas, Mücke, Pugzlys, Baltuška, Shim, Schrauth, Gaeta, H-García, Plaja, Becker, J-Becker, Murnane and Kapteyn9] and provides a route to generate zeptosecond waveforms[Reference García, Hernández, Popmintchev, Murnane, Kapteyn, Becker, Becker and Plaja10]. Additionally, mid-IR ultrafast lasers are favorable in spectroscopy applications because they match with the resonance fingerprints of common molecules[Reference Woutersen, Emmerichs and Bakker11].
$\unicode[STIX]{x1D706}^{2}$
[Reference Popmintchev, Chen, Popmintchev, Arpin, Brown, Ališauskas, Andriukaitis, Balčiunas, Mücke, Pugzlys, Baltuška, Shim, Schrauth, Gaeta, H-García, Plaja, Becker, J-Becker, Murnane and Kapteyn9] and provides a route to generate zeptosecond waveforms[Reference García, Hernández, Popmintchev, Murnane, Kapteyn, Becker, Becker and Plaja10]. Additionally, mid-IR ultrafast lasers are favorable in spectroscopy applications because they match with the resonance fingerprints of common molecules[Reference Woutersen, Emmerichs and Bakker11].
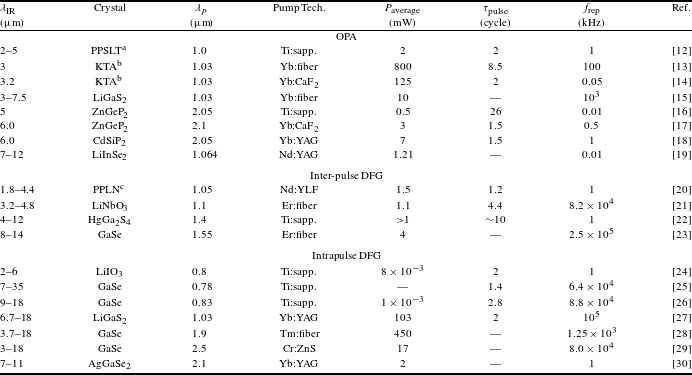
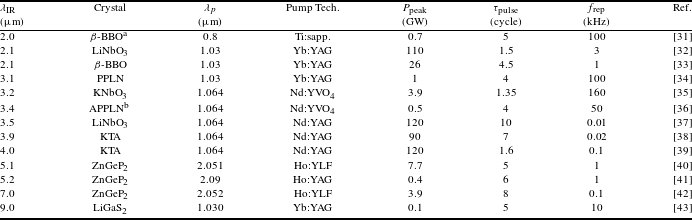
Owing to these interesting applications, the generation of intense mid-IR ultrafast lasers has attracted increasing interest from the optical community. Given the lack of traditional laser amplifiers beyond
![]() $3~\unicode[STIX]{x03BC}\text{m}$
, the common method is to convert an intense near-IR laser to the mid-IR spectral region via nonlinear frequency conversion, such as difference-frequency generation (DFG) and optical parametric amplification (OPA). Table 1 lists the typical ultrafast lasers in the mid-IR and long-wave IR ranges, which are generated by DFG or OPA based on different nonlinear crystals[Reference Brida, Marangoni, Manzoni, De Silvestri and Cerullo12–Reference Novák, Krogen, Kroh, Mocek, Kärtner and Hong30]. Limited by the detrimental effects of nonlinear self-focusing and optical damage, these IR pulses have relatively low nJ to sub-mJ energies. To generate more intense mid-IR pulses, optical parametric chirped-pulse amplification (OPCPA) should be used, which is a combination of OPA and CPA. As listed in Table 2, OPCPA currently supports GW-scale pulses in the spectral range from 2 to
$3~\unicode[STIX]{x03BC}\text{m}$
, the common method is to convert an intense near-IR laser to the mid-IR spectral region via nonlinear frequency conversion, such as difference-frequency generation (DFG) and optical parametric amplification (OPA). Table 1 lists the typical ultrafast lasers in the mid-IR and long-wave IR ranges, which are generated by DFG or OPA based on different nonlinear crystals[Reference Brida, Marangoni, Manzoni, De Silvestri and Cerullo12–Reference Novák, Krogen, Kroh, Mocek, Kärtner and Hong30]. Limited by the detrimental effects of nonlinear self-focusing and optical damage, these IR pulses have relatively low nJ to sub-mJ energies. To generate more intense mid-IR pulses, optical parametric chirped-pulse amplification (OPCPA) should be used, which is a combination of OPA and CPA. As listed in Table 2, OPCPA currently supports GW-scale pulses in the spectral range from 2 to
![]() $9~\unicode[STIX]{x03BC}\text{m}$
[Reference Shamir, Rothhardt, Hädrich, Demmler, Tschernajew, Limpert and Tünnermann31–Reference Qu, Liang, Liu, Zou, Li, Wang and Zhang43]. The durations of mid-IR pulses, based on either OPA or OPCPA, are as short as a few optical cycles. Generally, OPA can generate shorter pulses than OPCPA due to shorter crystals and less dispersion.
$9~\unicode[STIX]{x03BC}\text{m}$
[Reference Shamir, Rothhardt, Hädrich, Demmler, Tschernajew, Limpert and Tünnermann31–Reference Qu, Liang, Liu, Zou, Li, Wang and Zhang43]. The durations of mid-IR pulses, based on either OPA or OPCPA, are as short as a few optical cycles. Generally, OPA can generate shorter pulses than OPCPA due to shorter crystals and less dispersion.
Table 1. Performance characteristics of long-wavelength OPA/DFG systems.
a PPSLT, periodically poled stoichiometric
![]() $\text{LiTaO}_{3}$
.
$\text{LiTaO}_{3}$
.
b KTA,
![]() $\text{KTiOAsO}_{4}$
.
$\text{KTiOAsO}_{4}$
.
c PPLN, periodically poled
![]() $\text{LiNbO}_{3}$
.
$\text{LiNbO}_{3}$
.
Table 2. Performance characteristics of long-wavelength OPCPA systems.
a
![]() $\unicode[STIX]{x1D6FD}$
-BBO,
$\unicode[STIX]{x1D6FD}$
-BBO,
![]() $\unicode[STIX]{x1D6FD}$
-phase
$\unicode[STIX]{x1D6FD}$
-phase
![]() $\text{BaB}_{2}\text{O}_{4}$
.
$\text{BaB}_{2}\text{O}_{4}$
.
b APPLN, aperiodically poled
![]() $\text{LiNbO}_{3}$
.
$\text{LiNbO}_{3}$
.
The performance of ultrafast OPA and OPCPA significantly depends on nonlinear crystals. In the ultrafast systems listed in Tables 1 and 2, the mid-IR crystals include both oxides and nonoxides. The oxide crystals are characterized by a high damage threshold and large crystal size, so they can produce high-peak-power mid-IR pulses. For example,
![]() $\text{LiNbO}_{3}$
and KTA crystals have produced
$\text{LiNbO}_{3}$
and KTA crystals have produced
![]() ${>}100~\text{GW}$
pulses at
${>}100~\text{GW}$
pulses at
![]() $3.5~\unicode[STIX]{x03BC}\text{m}$
[Reference Zhao, Zhong, Yuan, Xie, Wang, Ma and Qian37] and
$3.5~\unicode[STIX]{x03BC}\text{m}$
[Reference Zhao, Zhong, Yuan, Xie, Wang, Ma and Qian37] and
![]() $4~\unicode[STIX]{x03BC}\text{m}$
[Reference Wang, Li, Li, Su, Shao, Li, Wang, Wang, Zhao, Peng, Leng, Li and Xu39], respectively. However, it is difficult to produce mid-IR pulses beyond
$4~\unicode[STIX]{x03BC}\text{m}$
[Reference Wang, Li, Li, Su, Shao, Li, Wang, Wang, Zhao, Peng, Leng, Li and Xu39], respectively. However, it is difficult to produce mid-IR pulses beyond
![]() $5~\unicode[STIX]{x03BC}\text{m}$
with the commonly used oxide crystals due to their limited transparent ranges, as shown in Figure 1. Currently, the generation of mid-IR pulses beyond
$5~\unicode[STIX]{x03BC}\text{m}$
with the commonly used oxide crystals due to their limited transparent ranges, as shown in Figure 1. Currently, the generation of mid-IR pulses beyond
![]() $5~\unicode[STIX]{x03BC}\text{m}$
mainly relies on nonoxide semiconductor crystals whose IR transparent regions can extend beyond
$5~\unicode[STIX]{x03BC}\text{m}$
mainly relies on nonoxide semiconductor crystals whose IR transparent regions can extend beyond
![]() $10~\unicode[STIX]{x03BC}\text{m}$
. However, semiconductor crystals have much lower damage thresholds, as shown in Figure 1. Moreover, their sizes are limited by growth method. Among these crystals, the
$10~\unicode[STIX]{x03BC}\text{m}$
. However, semiconductor crystals have much lower damage thresholds, as shown in Figure 1. Moreover, their sizes are limited by growth method. Among these crystals, the
![]() $\text{ZnGeP}_{2}$
(ZGP) crystal is commercially available with an aperture up to 1 inch (
$\text{ZnGeP}_{2}$
(ZGP) crystal is commercially available with an aperture up to 1 inch (
![]() $1~\text{inch}=2.54~\text{cm}$
)[Reference Zawilski, Schunemann, Setzler and Pollak44], so it has been adopted in recent OPCPA systems beyond
$1~\text{inch}=2.54~\text{cm}$
)[Reference Zawilski, Schunemann, Setzler and Pollak44], so it has been adopted in recent OPCPA systems beyond
![]() $5~\unicode[STIX]{x03BC}\text{m}$
[Reference Grafenstein, Bock, Ueberschaer, Zawilski, Schunemann, Griebner and Elsaesser40–Reference Elu, Steinle, Sánchez, Maidment, Zawilski, Schunemann, Zeitner, S-Boisson and Biegert42]. Unfortunately, most semiconductor crystals, including ZGP, exhibit strong absorption to the well-established pump laser at approximately
$5~\unicode[STIX]{x03BC}\text{m}$
[Reference Grafenstein, Bock, Ueberschaer, Zawilski, Schunemann, Griebner and Elsaesser40–Reference Elu, Steinle, Sánchez, Maidment, Zawilski, Schunemann, Zeitner, S-Boisson and Biegert42]. Unfortunately, most semiconductor crystals, including ZGP, exhibit strong absorption to the well-established pump laser at approximately
![]() $1~\unicode[STIX]{x03BC}\text{m}$
. On the other hand, their bandgap energy (e.g., ZGP: 1.75 eV;
$1~\unicode[STIX]{x03BC}\text{m}$
. On the other hand, their bandgap energy (e.g., ZGP: 1.75 eV;
![]() $\text{CdSiP}_{2}$
(CSP): 2.41 eV) is usually about or smaller than twice the photon energy (
$\text{CdSiP}_{2}$
(CSP): 2.41 eV) is usually about or smaller than twice the photon energy (
![]() ${\sim}1.25~\text{eV}$
) of the
${\sim}1.25~\text{eV}$
) of the
![]() $1~\unicode[STIX]{x03BC}\text{m}$
pump laser, so they also suffer from severe two-photon absorption of the pump. Therefore, mid-IR OPCPA systems with semiconductor crystals are often pumped by a specially developed Ho-based laser at
$1~\unicode[STIX]{x03BC}\text{m}$
pump laser, so they also suffer from severe two-photon absorption of the pump. Therefore, mid-IR OPCPA systems with semiconductor crystals are often pumped by a specially developed Ho-based laser at
![]() $2~\unicode[STIX]{x03BC}\text{m}$
. One exception is the
$2~\unicode[STIX]{x03BC}\text{m}$
. One exception is the
![]() $\text{LiGaS}_{2}$
-crystal-based OPCPA, in which the large bandgap energy (3.62 eV) of the
$\text{LiGaS}_{2}$
-crystal-based OPCPA, in which the large bandgap energy (3.62 eV) of the
![]() $\text{LiGaS}_{2}$
crystal allows the direct pump with mature
$\text{LiGaS}_{2}$
crystal allows the direct pump with mature
![]() $1~\unicode[STIX]{x03BC}\text{m}$
laser source[Reference Qu, Liang, Liu, Zou, Li, Wang and Zhang43].
$1~\unicode[STIX]{x03BC}\text{m}$
laser source[Reference Qu, Liang, Liu, Zou, Li, Wang and Zhang43].
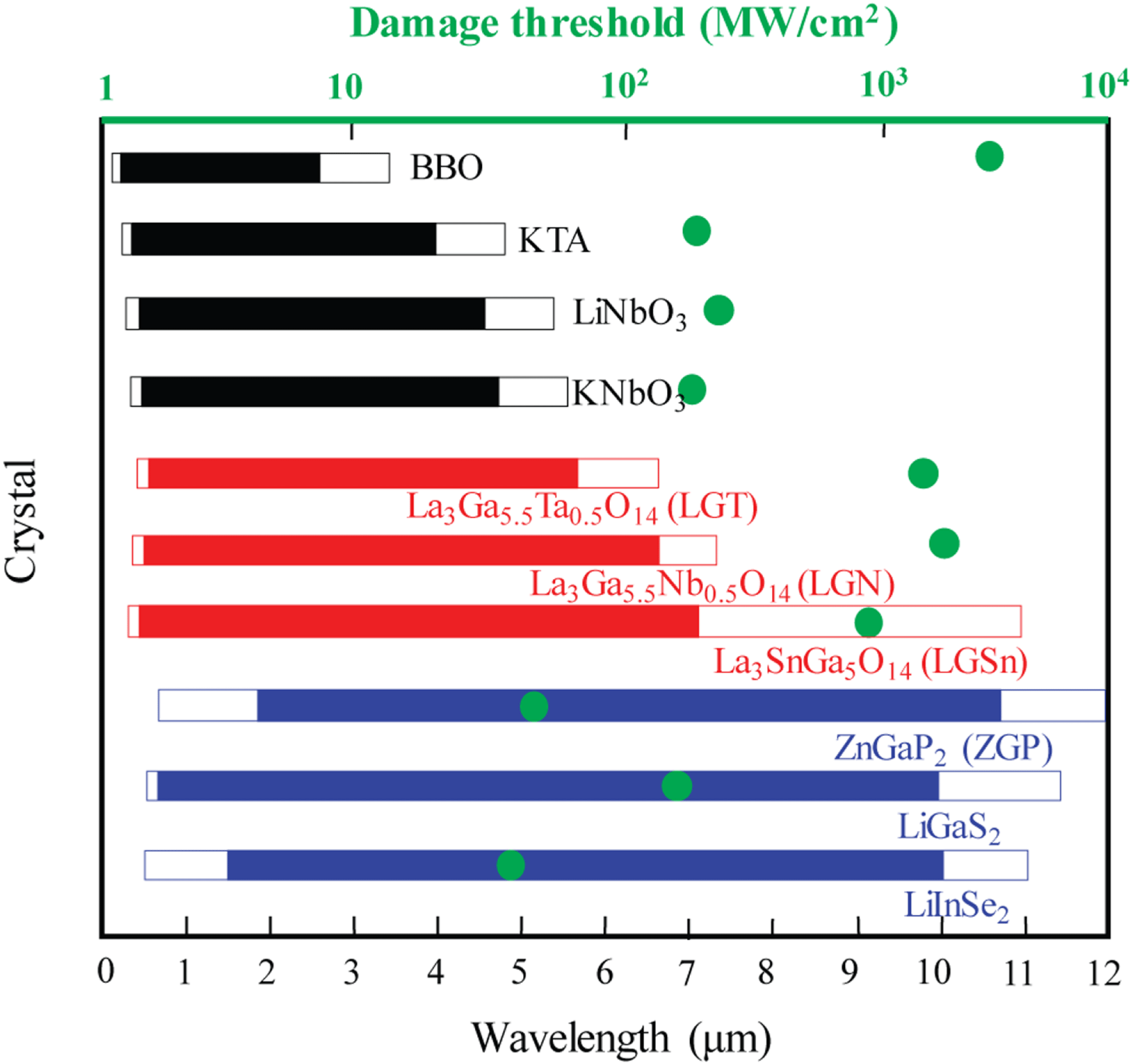
Figure 1. Transparent regions and damage thresholds of commonly used nonlinear crystals. The full (color) bar marks the transparent regions at zero (half) transmittance. The black, red and blue bars correspond to conventional oxide crystals, new langasite oxide crystals and semiconductor crystals, respectively. The green circles mark the damage thresholds with 10 ns pulses at
![]() $2.05~\unicode[STIX]{x03BC}\text{m}$
for the ZGP crystal and 10 ns pulses at 1064 nm for other crystals. Most of the data come from the book, D. N. Nikogosyan, Nonlinear Optical Crystals: A Complete Survey (Springer, New York, 2006). Other data for langasite oxides come from Refs. [Reference Ma, Wang, Hu, Yuan, Xie, Zhu, Yu, Zhang, Wang and Qian45–Reference Lu, Xu, Yu, Fu, Zhang, Segonds, Boulanger, Zhang and Wang48] and [Reference Lan, Liang, Jiang, Zhang, Yu, Liu, Zhang, Wang and Wu51].
$2.05~\unicode[STIX]{x03BC}\text{m}$
for the ZGP crystal and 10 ns pulses at 1064 nm for other crystals. Most of the data come from the book, D. N. Nikogosyan, Nonlinear Optical Crystals: A Complete Survey (Springer, New York, 2006). Other data for langasite oxides come from Refs. [Reference Ma, Wang, Hu, Yuan, Xie, Zhu, Yu, Zhang, Wang and Qian45–Reference Lu, Xu, Yu, Fu, Zhang, Segonds, Boulanger, Zhang and Wang48] and [Reference Lan, Liang, Jiang, Zhang, Yu, Liu, Zhang, Wang and Wu51].
In this paper, we put forward a
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
high-power OPCPA proposal based on a langasite oxide
$5.2~\unicode[STIX]{x03BC}\text{m}$
high-power OPCPA proposal based on a langasite oxide
![]() $\text{La}_{3}\text{Ga}_{5.5}\text{Nb}_{0.5}\text{O}_{14}$
(LGN) crystal. The langasite oxides, e.g., LGN,
$\text{La}_{3}\text{Ga}_{5.5}\text{Nb}_{0.5}\text{O}_{14}$
(LGN) crystal. The langasite oxides, e.g., LGN,
![]() $\text{La}_{3}\text{Ga}_{5.5}\text{Ta}_{0.5}\text{O}_{14}$
(LGT) and
$\text{La}_{3}\text{Ga}_{5.5}\text{Ta}_{0.5}\text{O}_{14}$
(LGT) and
![]() $\text{La}_{3}\text{Ga}_{5}\text{SiO}_{14}$
(LGS), have been used as piezoelectric and electro-optic crystals for a long time. Only in recent years have langasite oxides been found to be superior mid-IR nonlinear crystals[Reference Ma, Wang, Hu, Yuan, Xie, Zhu, Yu, Zhang, Wang and Qian45–Reference Boursier, Segonds, Boulanger, Félix, Debray, Jegouso, Ménaert, Roshchupkin and Shoji49]. As shown in Figure 1, their IR cutoff transparent wavelengths extend to the region of
$\text{La}_{3}\text{Ga}_{5}\text{SiO}_{14}$
(LGS), have been used as piezoelectric and electro-optic crystals for a long time. Only in recent years have langasite oxides been found to be superior mid-IR nonlinear crystals[Reference Ma, Wang, Hu, Yuan, Xie, Zhu, Yu, Zhang, Wang and Qian45–Reference Boursier, Segonds, Boulanger, Félix, Debray, Jegouso, Ménaert, Roshchupkin and Shoji49]. As shown in Figure 1, their IR cutoff transparent wavelengths extend to the region of
![]() $5{-}10~\unicode[STIX]{x03BC}\text{m}$
(e.g.,
$5{-}10~\unicode[STIX]{x03BC}\text{m}$
(e.g.,
![]() ${\sim}7.5~\unicode[STIX]{x03BC}\text{m}$
for LGN crystal[Reference Lu, Xu, Yu, Fu, Zhang, Segonds, Boulanger, Zhang and Wang48]), longer than those of commonly used oxides. At the same time, langasite oxides are transparent to the developed pump lasers at approximately
${\sim}7.5~\unicode[STIX]{x03BC}\text{m}$
for LGN crystal[Reference Lu, Xu, Yu, Fu, Zhang, Segonds, Boulanger, Zhang and Wang48]), longer than those of commonly used oxides. At the same time, langasite oxides are transparent to the developed pump lasers at approximately
![]() $1~\unicode[STIX]{x03BC}\text{m}$
, and they are also immune to the nonlinear two-photon absorption of the
$1~\unicode[STIX]{x03BC}\text{m}$
, and they are also immune to the nonlinear two-photon absorption of the
![]() $1~\unicode[STIX]{x03BC}\text{m}$
pump due to their relatively large bandgap energy (e.g., LGN: 4.43 eV). Some recent experimental works have demonstrated
$1~\unicode[STIX]{x03BC}\text{m}$
pump due to their relatively large bandgap energy (e.g., LGN: 4.43 eV). Some recent experimental works have demonstrated
![]() $4.7~\unicode[STIX]{x03BC}\text{m}$
DFG pumped by Ti:sapphire laser in LGT crystal[Reference Boursier, Archipovaite, Delagnes, Petit, Ernotte, Lassonde, Segonds, Boulanger, Petit, Légaré, Roshchupkin and Cormier46] and
$4.7~\unicode[STIX]{x03BC}\text{m}$
DFG pumped by Ti:sapphire laser in LGT crystal[Reference Boursier, Archipovaite, Delagnes, Petit, Ernotte, Lassonde, Segonds, Boulanger, Petit, Légaré, Roshchupkin and Cormier46] and
![]() $6.5~\unicode[STIX]{x03BC}\text{m}$
DFG pumped by 1064 nm laser in LGN crystal[Reference Guo, Lu, Segonds, Debray, Yu, Zhang, Wang and Boulanger47]. The large bandgap energy of langasite oxides also enables them to have higher damage thresholds than semiconductor crystals. More importantly, they can be grown with a large size up to 4 inches by the Czochralski method[Reference Boursier, Segonds, Boulanger, Félix, Debray, Jegouso, Ménaert, Roshchupkin and Shoji49]. Therefore, langasite oxides can directly convert a well-established high-energy
$6.5~\unicode[STIX]{x03BC}\text{m}$
DFG pumped by 1064 nm laser in LGN crystal[Reference Guo, Lu, Segonds, Debray, Yu, Zhang, Wang and Boulanger47]. The large bandgap energy of langasite oxides also enables them to have higher damage thresholds than semiconductor crystals. More importantly, they can be grown with a large size up to 4 inches by the Czochralski method[Reference Boursier, Segonds, Boulanger, Félix, Debray, Jegouso, Ménaert, Roshchupkin and Shoji49]. Therefore, langasite oxides can directly convert a well-established high-energy
![]() $1~\unicode[STIX]{x03BC}\text{m}$
laser to mid-IR lasers beyond
$1~\unicode[STIX]{x03BC}\text{m}$
laser to mid-IR lasers beyond
![]() $5~\unicode[STIX]{x03BC}\text{m}$
with a high peak power scalability. By contrast, the peak power of the
$5~\unicode[STIX]{x03BC}\text{m}$
with a high peak power scalability. By contrast, the peak power of the
![]() $1~\unicode[STIX]{x03BC}\text{m}$
pumped OPCPA based on the semiconductor
$1~\unicode[STIX]{x03BC}\text{m}$
pumped OPCPA based on the semiconductor
![]() $\text{LiGaS}_{2}$
crystal is significantly limited by the low damage threshold (lower than those of the langasite oxides by almost one order of magnitude) and the small available size (currently limited to
$\text{LiGaS}_{2}$
crystal is significantly limited by the low damage threshold (lower than those of the langasite oxides by almost one order of magnitude) and the small available size (currently limited to
![]() $7~\text{mm}\times 7~\text{mm}$
[Reference Qu, Liang, Liu, Zou, Li, Wang and Zhang43]) of
$7~\text{mm}\times 7~\text{mm}$
[Reference Qu, Liang, Liu, Zou, Li, Wang and Zhang43]) of
![]() $\text{LiGaS}_{2}$
crystal. In this study, we design a
$\text{LiGaS}_{2}$
crystal. In this study, we design a
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
OPCPA system with LGN crystals and a commercially available 200 W, 1030 nm Yb:YAG thin-disk pump laser. Such a mid-IR laser source combines a 0.13 TW peak power, a seven-cycle pulse duration, a 1 kHz repetition rate and a stable carrier–envelope phase (CEP) and can find widespread applications in strong-field physics and attosecond science[Reference Wolter, Pullen, Baudisch, Sclafani, Hemmer, Senftleben, Schröter, Ullrich, Moshammer and Biegert50].
$5.2~\unicode[STIX]{x03BC}\text{m}$
OPCPA system with LGN crystals and a commercially available 200 W, 1030 nm Yb:YAG thin-disk pump laser. Such a mid-IR laser source combines a 0.13 TW peak power, a seven-cycle pulse duration, a 1 kHz repetition rate and a stable carrier–envelope phase (CEP) and can find widespread applications in strong-field physics and attosecond science[Reference Wolter, Pullen, Baudisch, Sclafani, Hemmer, Senftleben, Schröter, Ullrich, Moshammer and Biegert50].
2 Source architecture
The phase-matching (PM) condition is the major factor that governs OPCPA. In the whole paper, we define the three interacting waves of the highest, moderate and lowest frequencies as ‘pump’, ‘signal’ and ‘idler’, respectively (i.e.,
![]() $\unicode[STIX]{x1D714}_{p}>\unicode[STIX]{x1D714}_{s}>\unicode[STIX]{x1D714}_{i}$
). Under this definition, the mid-IR pulse corresponds to ‘idler’ in the following demonstrations. First, we compare the PM performance between the LGN crystal and the widely used
$\unicode[STIX]{x1D714}_{p}>\unicode[STIX]{x1D714}_{s}>\unicode[STIX]{x1D714}_{i}$
). Under this definition, the mid-IR pulse corresponds to ‘idler’ in the following demonstrations. First, we compare the PM performance between the LGN crystal and the widely used
![]() $\text{LiGaS}_{2}$
crystal, both of which are pumped with 1030 nm lasers. Most of the currently reported OPCPA experiments based on
$\text{LiGaS}_{2}$
crystal, both of which are pumped with 1030 nm lasers. Most of the currently reported OPCPA experiments based on
![]() $\text{LiGaS}_{2}$
crystals are implemented in the
$\text{LiGaS}_{2}$
crystals are implemented in the
![]() $XY$
plane with Type-II (
$XY$
plane with Type-II (
![]() $e_{p}\rightarrow o_{s}+e_{i}$
) PM[Reference Qu, Liang, Liu, Zou, Li, Wang and Zhang43]. We calculate the PM curves of
$e_{p}\rightarrow o_{s}+e_{i}$
) PM[Reference Qu, Liang, Liu, Zou, Li, Wang and Zhang43]. We calculate the PM curves of
![]() $\text{LiGaS}_{2}$
crystal with the same crystal plane and PM type as used in the reported experiments. In a collinear configuration that is widely used in experiments, we find that the
$\text{LiGaS}_{2}$
crystal with the same crystal plane and PM type as used in the reported experiments. In a collinear configuration that is widely used in experiments, we find that the
![]() $\text{LiGaS}_{2}$
crystal can support broadband PM for the mid-IR wavelength around
$\text{LiGaS}_{2}$
crystal can support broadband PM for the mid-IR wavelength around
![]() $9~\unicode[STIX]{x03BC}\text{m}$
rather than our concerned
$9~\unicode[STIX]{x03BC}\text{m}$
rather than our concerned
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
(black curve in Figure 2(a)). In a noncollinear configuration, the
$5.2~\unicode[STIX]{x03BC}\text{m}$
(black curve in Figure 2(a)). In a noncollinear configuration, the
![]() $\text{LiGaS}_{2}$
crystal cannot support PM when the mid-IR pulse is directly seeded; conversely, PM can be found in
$\text{LiGaS}_{2}$
crystal cannot support PM when the mid-IR pulse is directly seeded; conversely, PM can be found in
![]() $\text{LiGaS}_{2}$
crystal if seeded with near-IR pulse, but its bandwidth is limited around our concerned
$\text{LiGaS}_{2}$
crystal if seeded with near-IR pulse, but its bandwidth is limited around our concerned
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
idler wavelength as implied by the noncollinear results in Figure 2(a). Therefore, we conclude that the
$5.2~\unicode[STIX]{x03BC}\text{m}$
idler wavelength as implied by the noncollinear results in Figure 2(a). Therefore, we conclude that the
![]() $\text{LiGaS}_{2}$
crystal is not suitable in our design. The calculation results for Type-I (
$\text{LiGaS}_{2}$
crystal is not suitable in our design. The calculation results for Type-I (
![]() $o_{p}\rightarrow e_{s}+e_{i}$
) PM in LGN crystal show that it can allow the direct seeding with mid-IR pulses in noncollinear configuration, but its bandwidth is still limited around the targeted wavelength of
$o_{p}\rightarrow e_{s}+e_{i}$
) PM in LGN crystal show that it can allow the direct seeding with mid-IR pulses in noncollinear configuration, but its bandwidth is still limited around the targeted wavelength of
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
(Figure 2(b)). The expected broadband PM for
$5.2~\unicode[STIX]{x03BC}\text{m}$
(Figure 2(b)). The expected broadband PM for
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
mid-IR pulses appears in LGN crystal with the Type-II (
$5.2~\unicode[STIX]{x03BC}\text{m}$
mid-IR pulses appears in LGN crystal with the Type-II (
![]() $o_{p}\rightarrow e_{s}+o_{i}$
) noncollinear configuration, in which the best noncollinear angle
$o_{p}\rightarrow e_{s}+o_{i}$
) noncollinear configuration, in which the best noncollinear angle
![]() $\unicode[STIX]{x1D6FC}$
between the pump and the mid-IR pulses is about
$\unicode[STIX]{x1D6FC}$
between the pump and the mid-IR pulses is about
![]() $6^{\circ }$
inside the crystal. In addition, the Type-II PM outperforms the Type-I PM in the effective second-order nonlinear coefficients
$6^{\circ }$
inside the crystal. In addition, the Type-II PM outperforms the Type-I PM in the effective second-order nonlinear coefficients
![]() $d_{\text{eff}}$
as well, because
$d_{\text{eff}}$
as well, because
![]() $d_{\text{eff}}$
of Type-I PM and Type-II PM in LGN crystals depend on the PM angle
$d_{\text{eff}}$
of Type-I PM and Type-II PM in LGN crystals depend on the PM angle
![]() $\unicode[STIX]{x1D703}$
according to
$\unicode[STIX]{x1D703}$
according to
![]() $d_{\text{eff}}=d_{11}\cos ^{2}\unicode[STIX]{x1D703}$
and
$d_{\text{eff}}=d_{11}\cos ^{2}\unicode[STIX]{x1D703}$
and
![]() $d_{11}\cos \unicode[STIX]{x1D703}$
, respectively[Reference Lu, Xu, Yu, Fu, Zhang, Segonds, Boulanger, Zhang and Wang48], where
$d_{11}\cos \unicode[STIX]{x1D703}$
, respectively[Reference Lu, Xu, Yu, Fu, Zhang, Segonds, Boulanger, Zhang and Wang48], where
![]() $d_{11}=2.9~\text{pm}/\text{V}$
[Reference Guo, Lu, Segonds, Debray, Yu, Zhang, Wang and Boulanger47]. Therefore, we adopt Type-II noncollinear PM in LGN crystals for building our OPCPA system.
$d_{11}=2.9~\text{pm}/\text{V}$
[Reference Guo, Lu, Segonds, Debray, Yu, Zhang, Wang and Boulanger47]. Therefore, we adopt Type-II noncollinear PM in LGN crystals for building our OPCPA system.
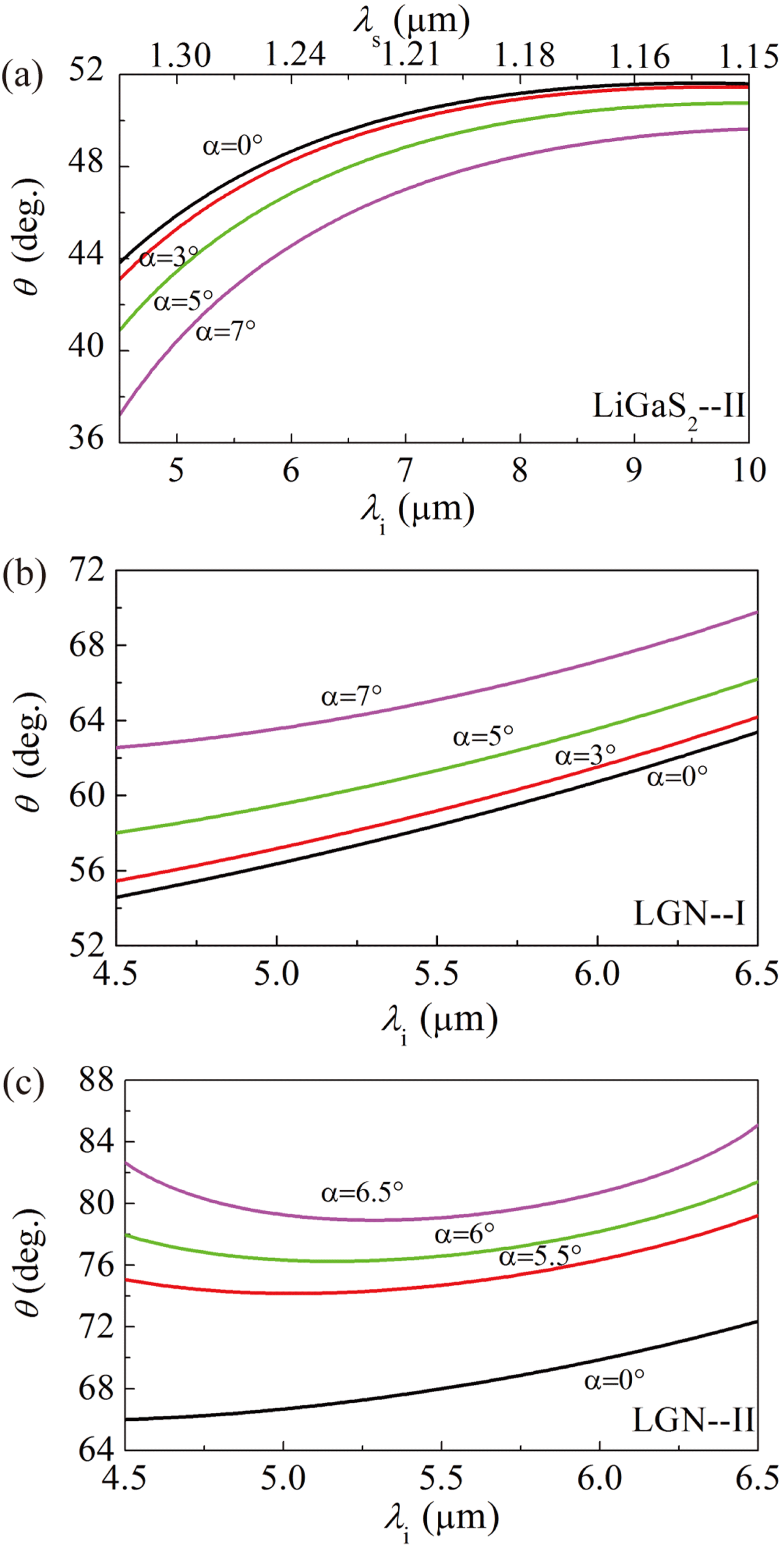
Figure 2. PM for noncollinear OPCPA pumped by 1030 nm laser. (a) Type-II (
![]() $e_{p}\rightarrow o_{s}+e_{i}$
) PM in
$e_{p}\rightarrow o_{s}+e_{i}$
) PM in
![]() $XY$
plane of
$XY$
plane of
![]() $\text{LiGaS}_{2}$
crystal; (b) Type-I (
$\text{LiGaS}_{2}$
crystal; (b) Type-I (
![]() $o_{p}\rightarrow e_{s}+e_{i}$
) PM in LGN crystal; (c) Type-II (
$o_{p}\rightarrow e_{s}+e_{i}$
) PM in LGN crystal; (c) Type-II (
![]() $o_{p}\rightarrow e_{s}+o_{i}$
) PM in LGN crystal.
$o_{p}\rightarrow e_{s}+o_{i}$
) PM in LGN crystal.
![]() $\unicode[STIX]{x1D6FC}$
is the intersecting angle between pump and mid-IR beams inside the crystal;
$\unicode[STIX]{x1D6FC}$
is the intersecting angle between pump and mid-IR beams inside the crystal;
![]() $\unicode[STIX]{x1D6FC}=0^{\circ }$
corresponds to the collinear configuration.
$\unicode[STIX]{x1D6FC}=0^{\circ }$
corresponds to the collinear configuration.

Figure 3. Schematic setup of the proposed
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
TW-class OPCPA system based on oxide LGN crystals. All of the hardware devices in the gray background are commercially available. The reflection-induced losses in the LGN crystals and Si plate are neglected. Three OPCPA stages are pumped with the same intensity of
$5.2~\unicode[STIX]{x03BC}\text{m}$
TW-class OPCPA system based on oxide LGN crystals. All of the hardware devices in the gray background are commercially available. The reflection-induced losses in the LGN crystals and Si plate are neglected. Three OPCPA stages are pumped with the same intensity of
![]() $50~\text{GW}/\text{cm}^{2}$
.
$50~\text{GW}/\text{cm}^{2}$
.
Based on the unique PM characteristics of LGN, we design a
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
, few-cycle, high-power OPCPA system including generation, stretching, amplification and compression stages. The whole system is schematically shown in Figure 3. The system makes full use of two commercially available advanced ultrafast lasers: an octave-spanning Ti:sapphire laser and a Yb:YAG thin-disk pump laser. The octave-spanning Ti:sapphire oscillator (e.g., Venteon series, Laser Quantum) is an ideal front end for a few-cycle OPCPA system. Its broad spectrum covering 600–1200 nm not only allows the generation of sub-6-fs pulses at 800 nm but also provides sufficient pulse energy at 1030 nm for seeding the Yb:YAG thin-disk amplifier. The two output pulses are intrinsically self-synchronized with each other. The 800 nm few-cycle pulses can be further amplified by near-IR OPCPA to an energy
$5.2~\unicode[STIX]{x03BC}\text{m}$
, few-cycle, high-power OPCPA system including generation, stretching, amplification and compression stages. The whole system is schematically shown in Figure 3. The system makes full use of two commercially available advanced ultrafast lasers: an octave-spanning Ti:sapphire laser and a Yb:YAG thin-disk pump laser. The octave-spanning Ti:sapphire oscillator (e.g., Venteon series, Laser Quantum) is an ideal front end for a few-cycle OPCPA system. Its broad spectrum covering 600–1200 nm not only allows the generation of sub-6-fs pulses at 800 nm but also provides sufficient pulse energy at 1030 nm for seeding the Yb:YAG thin-disk amplifier. The two output pulses are intrinsically self-synchronized with each other. The 800 nm few-cycle pulses can be further amplified by near-IR OPCPA to an energy
![]() ${>}15~\unicode[STIX]{x03BC}\text{J}$
(e.g., the Venteon OPCPA from Laser Quantum). The 1030 nm output can be amplified successively by a fiber laser and a Yb:YAG thin-disk laser to an energy of 200 mJ (e.g., TRUMPF Dira 200 series). The following analyses and simulations in this paper are based on these output characteristics.
${>}15~\unicode[STIX]{x03BC}\text{J}$
(e.g., the Venteon OPCPA from Laser Quantum). The 1030 nm output can be amplified successively by a fiber laser and a Yb:YAG thin-disk laser to an energy of 200 mJ (e.g., TRUMPF Dira 200 series). The following analyses and simulations in this paper are based on these output characteristics.
The mid-IR seeding pulse for
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
OPCPA is obtained via intrapulse DFG between the spectral components of the octave-spanning Ti:sapphire laser, which is passively CEP-stable because any CEP jitter can be canceled by its intraband DFG process[Reference Baltuška, Fuji and Kobayashi52]. The CEP stability of the drive laser is necessary for some strong-field processes, e.g., HHG. With direct Ti:sapphire laser pump, this intrapulse DFG method has been used to generate mid-IR pulses beyond
$5.2~\unicode[STIX]{x03BC}\text{m}$
OPCPA is obtained via intrapulse DFG between the spectral components of the octave-spanning Ti:sapphire laser, which is passively CEP-stable because any CEP jitter can be canceled by its intraband DFG process[Reference Baltuška, Fuji and Kobayashi52]. The CEP stability of the drive laser is necessary for some strong-field processes, e.g., HHG. With direct Ti:sapphire laser pump, this intrapulse DFG method has been used to generate mid-IR pulses beyond
![]() $5~\unicode[STIX]{x03BC}\text{m}$
in both oxide
$5~\unicode[STIX]{x03BC}\text{m}$
in both oxide
![]() $\text{LiIO}_{3}$
crystal[Reference Zentgraf, Huber, Nielsen, Chemla and Kaindl24] and semiconductor GaSe crystal[Reference Huber, Brodschelm, Tauser and Leitenstorfer25, Reference Kaindl, Smith, Joschko, Hasselbeck, Woerner and Elsaesser26]. Currently, with specially developed
$\text{LiIO}_{3}$
crystal[Reference Zentgraf, Huber, Nielsen, Chemla and Kaindl24] and semiconductor GaSe crystal[Reference Huber, Brodschelm, Tauser and Leitenstorfer25, Reference Kaindl, Smith, Joschko, Hasselbeck, Woerner and Elsaesser26]. Currently, with specially developed
![]() $2~\unicode[STIX]{x03BC}\text{m}$
pump light sources, intrapulse DFG systems based on semiconductor GaSe[Reference Gaida, Gebhardt, Heuermann, Stutzki, Jauregui, A-Lopez, Schülzgen, A-Correa, Tünnermann, Pupeza and Limpert28, Reference Vasilyev, Moskalev, Smolski, Peppers, Mirov, Muraviev, Vodopyanov, Mirov and Gapontsev29] and
$2~\unicode[STIX]{x03BC}\text{m}$
pump light sources, intrapulse DFG systems based on semiconductor GaSe[Reference Gaida, Gebhardt, Heuermann, Stutzki, Jauregui, A-Lopez, Schülzgen, A-Correa, Tünnermann, Pupeza and Limpert28, Reference Vasilyev, Moskalev, Smolski, Peppers, Mirov, Muraviev, Vodopyanov, Mirov and Gapontsev29] and
![]() $\text{AgGaSe}_{2}$
[Reference Novák, Krogen, Kroh, Mocek, Kärtner and Hong30] crystals have been developed to generate tunable mid-IR pulses with higher conversion efficiencies. In our design, an intrapulse DFG based on oxide LGN crystal and pumped by an octave-spanning Ti:sapphire laser is explored to provide CEP-stable broadband
$\text{AgGaSe}_{2}$
[Reference Novák, Krogen, Kroh, Mocek, Kärtner and Hong30] crystals have been developed to generate tunable mid-IR pulses with higher conversion efficiencies. In our design, an intrapulse DFG based on oxide LGN crystal and pumped by an octave-spanning Ti:sapphire laser is explored to provide CEP-stable broadband
![]() $4{-}6~\unicode[STIX]{x03BC}\text{m}$
pulses for our
$4{-}6~\unicode[STIX]{x03BC}\text{m}$
pulses for our
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
OPCPA system.
$5.2~\unicode[STIX]{x03BC}\text{m}$
OPCPA system.
The high-power thin-disk Yb:YAG picosecond laser is selected as the pump source for our OPCPA system, which has many advantages over typical Nd:YAG or Nd:glass lasers. First, the laser can support a repetition rate above 1 kHz due to good heat dissipation of the thin-disk geometry. In contrast, a high-power Nd:YAG or Nd:glass rod-type laser usually operates at 10 Hz or less. Second, the picosecond thin-disk laser allows a higher pump intensity in the crystal because the damage threshold of nonlinear crystals increases as pump pulse duration decreases[Reference Stuart, Feit, Rubenchik, Shore and Perry53]. An increase in the pump intensity ensures a high gain in a shorter crystal and thereby favors a broader gain bandwidth. Third, a picosecond pumped OPCPA system naturally supports a high pulse contrast by confining the parametric fluorescence within the narrow window of the pump pulse[Reference Ma, Yuan, Wang, Zhu and Qian54]. The high-contrast mid-IR laser can avoid preplasma formation when interacting with solid targets[Reference Ma, Yuan, Wang, Xie, Zhu and Qian55]. Finally, the picosecond pump also reduces the required group delay dispersion (GDD) to chirp the mid-IR pulse and allows compression with bulk materials. The residual high-order dispersion after compression can be precompensated by a commercial acousto-optic programmable dispersion filter (AOPDF, e.g., Fastlite DAZZLER UWB-3500-7000).
The 200 mJ energy from Yb:YAG laser is divided into three parts of 5, 45 and 150 mJ to pump three OPCPA stages with LGN crystal length of 15, 12 and 7 mm, respectively. Three beams of pump light are telescoped into beam sizes of 2.1, 6.1 and 11.2 mm (full width at half maximum (FWHM)), respectively, so that three OPCPA stages can be pumped by the same intensity of
![]() $50~\text{GW}/\text{cm}^{2}$
. The mid-IR femtosecond idler pulses from intrapulse DFG are negatively stretched into 2.0 ps chirped pulses by the AOPDF. The required GDD can be provided by the AOPDF without the need for an additional stretcher. The mid-IR chirped pulses are amplified to
$50~\text{GW}/\text{cm}^{2}$
. The mid-IR femtosecond idler pulses from intrapulse DFG are negatively stretched into 2.0 ps chirped pulses by the AOPDF. The required GDD can be provided by the AOPDF without the need for an additional stretcher. The mid-IR chirped pulses are amplified to
![]() ${\sim}0.1$
, 2.8 and 16.5 mJ successively by three OPCPA stages. Due to the relatively low quantum efficiency, the overall conversion efficiency from the pump to the mid-IR pulse is approximately 8%. Bulk silicon (Si) plates compress the second-order dispersion of the amplified mid-IR chirped pulses, while the remaining high-order dispersion can be precompensated by the AOPDF. The broad gain bandwidth of OPCPA supports a transform-limited pulse duration of 120 fs, corresponding to seven cycles at
${\sim}0.1$
, 2.8 and 16.5 mJ successively by three OPCPA stages. Due to the relatively low quantum efficiency, the overall conversion efficiency from the pump to the mid-IR pulse is approximately 8%. Bulk silicon (Si) plates compress the second-order dispersion of the amplified mid-IR chirped pulses, while the remaining high-order dispersion can be precompensated by the AOPDF. The broad gain bandwidth of OPCPA supports a transform-limited pulse duration of 120 fs, corresponding to seven cycles at
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
. The output peak power reaches 0.13 TW, which is higher than that of state-of-the-art
$5.2~\unicode[STIX]{x03BC}\text{m}$
. The output peak power reaches 0.13 TW, which is higher than that of state-of-the-art
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
OPCPA systems by nearly two orders of magnitude.
$5.2~\unicode[STIX]{x03BC}\text{m}$
OPCPA systems by nearly two orders of magnitude.
3 Numerical model
All of the simulations in this paper are based on the refined Sellmeier equation of LGN given in Ref. [Reference Guo, Lu, Segonds, Debray, Yu, Zhang, Wang and Boulanger47],
where
![]() $\unicode[STIX]{x1D706}$
denotes the wavelength in units of
$\unicode[STIX]{x1D706}$
denotes the wavelength in units of
![]() $\unicode[STIX]{x03BC}\text{m}$
. Obviously, LGN is a positive uniaxial crystal (
$\unicode[STIX]{x03BC}\text{m}$
. Obviously, LGN is a positive uniaxial crystal (
![]() $n_{e}>n_{o}$
). Type-II PM (
$n_{e}>n_{o}$
). Type-II PM (
![]() $o_{p}\rightarrow e_{s}+o_{i}$
) is adopted in both intrapulse DFG and OPCPA stages. A three-dimensional numerical model is used to simulate the Type-II (
$o_{p}\rightarrow e_{s}+o_{i}$
) is adopted in both intrapulse DFG and OPCPA stages. A three-dimensional numerical model is used to simulate the Type-II (
![]() $o_{p}\rightarrow e_{s}+o_{i}$
) three-wave parametric interaction in LGN. This model takes the nonlinear refractive index into account to deal with the self-phase and cross-phase modulations[Reference Thai, Skrobol, Bates, Arisholm, Major, Krausz, Karsch and Biegert56, Reference Mücke, Sidorov, Dombi, Pugzlys, Baltuska, Alisauskas, Smilgevicius, Pocius, Giniunas, Danielius and Forget57]. By further considering the effects of spatial walkoff, diffraction, dispersion (up to third order) and idler absorption, the nonlinear coupled-wave equations under the slowly varying envelope approximation can be written as
$o_{p}\rightarrow e_{s}+o_{i}$
) three-wave parametric interaction in LGN. This model takes the nonlinear refractive index into account to deal with the self-phase and cross-phase modulations[Reference Thai, Skrobol, Bates, Arisholm, Major, Krausz, Karsch and Biegert56, Reference Mücke, Sidorov, Dombi, Pugzlys, Baltuska, Alisauskas, Smilgevicius, Pocius, Giniunas, Danielius and Forget57]. By further considering the effects of spatial walkoff, diffraction, dispersion (up to third order) and idler absorption, the nonlinear coupled-wave equations under the slowly varying envelope approximation can be written as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}A_{p}}{\unicode[STIX]{x2202}z}+\unicode[STIX]{x1D70C}_{p}\frac{\unicode[STIX]{x2202}A_{p}}{\unicode[STIX]{x2202}x}-\frac{i}{2k_{p}}\left(\frac{\unicode[STIX]{x2202}^{2}A_{p}}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}A_{p}}{\unicode[STIX]{x2202}y^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\mathop{\sum }_{m=1}^{m=3}\frac{(-i)^{m-1}\unicode[STIX]{x1D6FD}_{mp}}{m!}\frac{\unicode[STIX]{x2202}^{m}A_{p}}{\unicode[STIX]{x2202}t^{m}}=-i\frac{\unicode[STIX]{x1D714}_{p}d_{\text{eff}}}{n_{p}c}A_{s}A_{i}e^{i\unicode[STIX]{x0394}kz}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\unicode[STIX]{x1D700}_{0}\unicode[STIX]{x1D714}_{p}n_{p}n_{2p}}{2}\left(|A_{p}|^{2}+\frac{2}{3}|A_{s}|^{2}+2|A_{i}|^{2}\right)A_{p},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}A_{p}}{\unicode[STIX]{x2202}z}+\unicode[STIX]{x1D70C}_{p}\frac{\unicode[STIX]{x2202}A_{p}}{\unicode[STIX]{x2202}x}-\frac{i}{2k_{p}}\left(\frac{\unicode[STIX]{x2202}^{2}A_{p}}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}A_{p}}{\unicode[STIX]{x2202}y^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\mathop{\sum }_{m=1}^{m=3}\frac{(-i)^{m-1}\unicode[STIX]{x1D6FD}_{mp}}{m!}\frac{\unicode[STIX]{x2202}^{m}A_{p}}{\unicode[STIX]{x2202}t^{m}}=-i\frac{\unicode[STIX]{x1D714}_{p}d_{\text{eff}}}{n_{p}c}A_{s}A_{i}e^{i\unicode[STIX]{x0394}kz}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\unicode[STIX]{x1D700}_{0}\unicode[STIX]{x1D714}_{p}n_{p}n_{2p}}{2}\left(|A_{p}|^{2}+\frac{2}{3}|A_{s}|^{2}+2|A_{i}|^{2}\right)A_{p},\end{eqnarray}$$
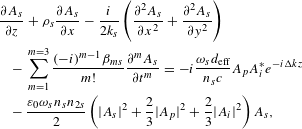 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}A_{s}}{\unicode[STIX]{x2202}z}+\unicode[STIX]{x1D70C}_{s}\frac{\unicode[STIX]{x2202}A_{s}}{\unicode[STIX]{x2202}x}-\frac{i}{2k_{s}}\left(\frac{\unicode[STIX]{x2202}^{2}A_{s}}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}A_{s}}{\unicode[STIX]{x2202}y^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\mathop{\sum }_{m=1}^{m=3}\frac{(-i)^{m-1}\unicode[STIX]{x1D6FD}_{ms}}{m!}\frac{\unicode[STIX]{x2202}^{m}A_{s}}{\unicode[STIX]{x2202}t^{m}}=-i\frac{\unicode[STIX]{x1D714}_{s}d_{\text{eff}}}{n_{s}c}A_{p}A_{i}^{\ast }e^{-i\unicode[STIX]{x0394}kz}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\unicode[STIX]{x1D700}_{0}\unicode[STIX]{x1D714}_{s}n_{s}n_{2s}}{2}\left(|A_{s}|^{2}+\frac{2}{3}|A_{p}|^{2}+\frac{2}{3}|A_{i}|^{2}\right)A_{s},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}A_{s}}{\unicode[STIX]{x2202}z}+\unicode[STIX]{x1D70C}_{s}\frac{\unicode[STIX]{x2202}A_{s}}{\unicode[STIX]{x2202}x}-\frac{i}{2k_{s}}\left(\frac{\unicode[STIX]{x2202}^{2}A_{s}}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}A_{s}}{\unicode[STIX]{x2202}y^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\mathop{\sum }_{m=1}^{m=3}\frac{(-i)^{m-1}\unicode[STIX]{x1D6FD}_{ms}}{m!}\frac{\unicode[STIX]{x2202}^{m}A_{s}}{\unicode[STIX]{x2202}t^{m}}=-i\frac{\unicode[STIX]{x1D714}_{s}d_{\text{eff}}}{n_{s}c}A_{p}A_{i}^{\ast }e^{-i\unicode[STIX]{x0394}kz}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\unicode[STIX]{x1D700}_{0}\unicode[STIX]{x1D714}_{s}n_{s}n_{2s}}{2}\left(|A_{s}|^{2}+\frac{2}{3}|A_{p}|^{2}+\frac{2}{3}|A_{i}|^{2}\right)A_{s},\end{eqnarray}$$
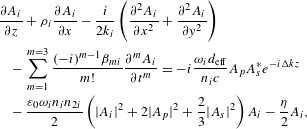 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}A_{i}}{\unicode[STIX]{x2202}z}+\unicode[STIX]{x1D70C}_{i}\frac{\unicode[STIX]{x2202}A_{i}}{\unicode[STIX]{x2202}x}-\frac{i}{2k_{i}}\left(\frac{\unicode[STIX]{x2202}^{2}A_{i}}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}A_{i}}{\unicode[STIX]{x2202}y^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\mathop{\sum }_{m=1}^{m=3}\frac{(-i)^{m-1}\unicode[STIX]{x1D6FD}_{mi}}{m!}\frac{\unicode[STIX]{x2202}^{m}A_{i}}{\unicode[STIX]{x2202}t^{m}}=-i\frac{\unicode[STIX]{x1D714}_{i}d_{\text{eff}}}{n_{i}c}A_{p}A_{s}^{\ast }e^{-i\unicode[STIX]{x0394}kz}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\unicode[STIX]{x1D700}_{0}\unicode[STIX]{x1D714}_{i}n_{i}n_{2i}}{2}\left(|A_{i}|^{2}+2|A_{p}|^{2}+\frac{2}{3}|A_{s}|^{2}\right)A_{i}-\frac{\unicode[STIX]{x1D702}}{2}A_{i},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}A_{i}}{\unicode[STIX]{x2202}z}+\unicode[STIX]{x1D70C}_{i}\frac{\unicode[STIX]{x2202}A_{i}}{\unicode[STIX]{x2202}x}-\frac{i}{2k_{i}}\left(\frac{\unicode[STIX]{x2202}^{2}A_{i}}{\unicode[STIX]{x2202}x^{2}}+\frac{\unicode[STIX]{x2202}^{2}A_{i}}{\unicode[STIX]{x2202}y^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\mathop{\sum }_{m=1}^{m=3}\frac{(-i)^{m-1}\unicode[STIX]{x1D6FD}_{mi}}{m!}\frac{\unicode[STIX]{x2202}^{m}A_{i}}{\unicode[STIX]{x2202}t^{m}}=-i\frac{\unicode[STIX]{x1D714}_{i}d_{\text{eff}}}{n_{i}c}A_{p}A_{s}^{\ast }e^{-i\unicode[STIX]{x0394}kz}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\unicode[STIX]{x1D700}_{0}\unicode[STIX]{x1D714}_{i}n_{i}n_{2i}}{2}\left(|A_{i}|^{2}+2|A_{p}|^{2}+\frac{2}{3}|A_{s}|^{2}\right)A_{i}-\frac{\unicode[STIX]{x1D702}}{2}A_{i},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
![]() $A_{j}$
,
$A_{j}$
,
![]() $\unicode[STIX]{x1D714}_{j}$
and
$\unicode[STIX]{x1D714}_{j}$
and
![]() $n_{j}$
are the complex envelope, carrier frequency and refractive index of wave
$n_{j}$
are the complex envelope, carrier frequency and refractive index of wave
![]() $j$
, and
$j$
, and
![]() $j=p$
,
$j=p$
,
![]() $s$
and
$s$
and
![]() $i$
refer to the pump, signal and idler, respectively.
$i$
refer to the pump, signal and idler, respectively.
![]() $c$
is the speed of light in vacuum.
$c$
is the speed of light in vacuum.
![]() $k_{j}=n_{j}w_{j}/c$
is the wavevector of wave
$k_{j}=n_{j}w_{j}/c$
is the wavevector of wave
![]() $j$
.
$j$
.
![]() $\unicode[STIX]{x0394}k=k_{p}-k_{s}-k_{i}$
is the phase mismatch among the interacting waves.
$\unicode[STIX]{x0394}k=k_{p}-k_{s}-k_{i}$
is the phase mismatch among the interacting waves.
![]() $d_{\text{eff}}$
is the effective nonlinear coefficient and is equal to
$d_{\text{eff}}$
is the effective nonlinear coefficient and is equal to
![]() $1.47$
and
$1.47$
and
![]() $0.7~\text{pm}/\text{V}$
in intrapulse DFG and OPCPA, respectively. The
$0.7~\text{pm}/\text{V}$
in intrapulse DFG and OPCPA, respectively. The
![]() $m$
th-order (
$m$
th-order (
![]() $m=1{-}3$
) dispersion coefficients of wave
$m=1{-}3$
) dispersion coefficients of wave
![]() $j$
,
$j$
,
![]() $\unicode[STIX]{x1D6FD}_{mj}=\unicode[STIX]{x2202}^{(m)}k_{j}/\unicode[STIX]{x2202}\unicode[STIX]{x1D714}^{(m)}$
, represent the inverse of group velocity, the group-velocity dispersion (GVD) and the third-order dispersion (TOD), respectively, which can be calculated with Equations (1) and (2).
$\unicode[STIX]{x1D6FD}_{mj}=\unicode[STIX]{x2202}^{(m)}k_{j}/\unicode[STIX]{x2202}\unicode[STIX]{x1D714}^{(m)}$
, represent the inverse of group velocity, the group-velocity dispersion (GVD) and the third-order dispersion (TOD), respectively, which can be calculated with Equations (1) and (2).
![]() $\unicode[STIX]{x1D70C}_{j}$
refers to the spatial walkoff angle of wave
$\unicode[STIX]{x1D70C}_{j}$
refers to the spatial walkoff angle of wave
![]() $j$
in the
$j$
in the
![]() $x$
direction induced by birefringence and noncollinearity. Specifically, an ordinary polarized wave has no birefringence-induced walkoff. Diffraction is taken into account in both the transverse spatial directions
$x$
direction induced by birefringence and noncollinearity. Specifically, an ordinary polarized wave has no birefringence-induced walkoff. Diffraction is taken into account in both the transverse spatial directions
![]() $x$
and
$x$
and
![]() $y$
.
$y$
.
![]() $n_{2j}$
is the nonlinear refractive index of wave
$n_{2j}$
is the nonlinear refractive index of wave
![]() $j$
. As the
$j$
. As the
![]() $n_{2}$
value of LGN crystal has not been reported, we assume that
$n_{2}$
value of LGN crystal has not been reported, we assume that
![]() $n_{2p}=n_{2s}=2\times 10^{-19}~\text{m}^{2}/\text{W}$
for near-IR pulses around
$n_{2p}=n_{2s}=2\times 10^{-19}~\text{m}^{2}/\text{W}$
for near-IR pulses around
![]() $1~\unicode[STIX]{x03BC}\text{m}$
and
$1~\unicode[STIX]{x03BC}\text{m}$
and
![]() $n_{2i}=1\times 10^{-19}~\text{m}^{2}/\text{W}$
for mid-IR pulses centered at
$n_{2i}=1\times 10^{-19}~\text{m}^{2}/\text{W}$
for mid-IR pulses centered at
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
in our simulations, which are estimated according to the reported
$5.2~\unicode[STIX]{x03BC}\text{m}$
in our simulations, which are estimated according to the reported
![]() $n_{2}$
value of LGT crystal at 343 nm[Reference Boursier, Archipovaite, Delagnes, Petit, Ernotte, Lassonde, Segonds, Boulanger, Petit, Légaré, Roshchupkin and Cormier46].
$n_{2}$
value of LGT crystal at 343 nm[Reference Boursier, Archipovaite, Delagnes, Petit, Ernotte, Lassonde, Segonds, Boulanger, Petit, Légaré, Roshchupkin and Cormier46].
![]() $\unicode[STIX]{x1D702}=15~\text{m}^{-1}$
represents the idler absorption coefficient at
$\unicode[STIX]{x1D702}=15~\text{m}^{-1}$
represents the idler absorption coefficient at
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
, which is calculated according to the transmission curve of LGN crystal given in Ref. [Reference Lu, Xu, Yu, Fu, Zhang, Segonds, Boulanger, Zhang and Wang48]. Equations (3)–(5) are numerically calculated by a symmetric split-step Fourier transform method and a fourth-order Runge–Kutta algorithm.
$5.2~\unicode[STIX]{x03BC}\text{m}$
, which is calculated according to the transmission curve of LGN crystal given in Ref. [Reference Lu, Xu, Yu, Fu, Zhang, Segonds, Boulanger, Zhang and Wang48]. Equations (3)–(5) are numerically calculated by a symmetric split-step Fourier transform method and a fourth-order Runge–Kutta algorithm.
4 Results and discussion
4.1 Intrapulse DFG for generating mid-IR seed pulses
The collinear intrapulse DFG between the short-wavelength (pump) and long-wavelength (signal) components of a single octave-spanning pulse can generate the mid-IR pulse (idler) for seeding subsequent OPCPA. Type-II PM (
![]() $o_{p}\rightarrow e_{s}+o_{i}$
) is adopted in the collinear intrapulse DFG because of a larger value of
$o_{p}\rightarrow e_{s}+o_{i}$
) is adopted in the collinear intrapulse DFG because of a larger value of
![]() $d_{\text{eff}}$
and an achievable longer mid-IR wavelength with the LGN crystal. Broadband mid-IR pulses can be obtained under the condition of
$d_{\text{eff}}$
and an achievable longer mid-IR wavelength with the LGN crystal. Broadband mid-IR pulses can be obtained under the condition of
![]() $\text{GVM}_{si}=0$
. Figure 4(a) plots the wavelength pairs of the signal and idler for various pump wavelengths when
$\text{GVM}_{si}=0$
. Figure 4(a) plots the wavelength pairs of the signal and idler for various pump wavelengths when
![]() $\text{GVM}_{si}=0$
is satisfied. With the pump and signal wavelengths located in the spectral range (600–1200 nm) of the octave-spanning pulse, broadband PM (
$\text{GVM}_{si}=0$
is satisfied. With the pump and signal wavelengths located in the spectral range (600–1200 nm) of the octave-spanning pulse, broadband PM (
![]() $\text{GVM}_{si}=0$
) can be achieved for mid-IR wavelengths within
$\text{GVM}_{si}=0$
) can be achieved for mid-IR wavelengths within
![]() $4.5$
–
$4.5$
–
![]() $6.5~\unicode[STIX]{x03BC}\text{m}$
when the PM angle
$6.5~\unicode[STIX]{x03BC}\text{m}$
when the PM angle
![]() $\unicode[STIX]{x1D703}$
is tuned from
$\unicode[STIX]{x1D703}$
is tuned from
![]() $58^{\circ }$
to
$58^{\circ }$
to
![]() $62^{\circ }$
. In the following analysis, we fix the angle at
$62^{\circ }$
. In the following analysis, we fix the angle at
![]() $\unicode[STIX]{x1D703}=59.50^{\circ }$
, corresponding to broadband PM among
$\unicode[STIX]{x1D703}=59.50^{\circ }$
, corresponding to broadband PM among
![]() $\unicode[STIX]{x1D706}_{p}=770~\text{nm}$
,
$\unicode[STIX]{x1D706}_{p}=770~\text{nm}$
,
![]() $\unicode[STIX]{x1D706}_{s}=904~\text{nm}$
and
$\unicode[STIX]{x1D706}_{s}=904~\text{nm}$
and
![]() $\unicode[STIX]{x1D706}_{i}=5.2~\unicode[STIX]{x03BC}\text{m}$
. We further calculate all the possible PM wavelengths at
$\unicode[STIX]{x1D706}_{i}=5.2~\unicode[STIX]{x03BC}\text{m}$
. We further calculate all the possible PM wavelengths at
![]() $\unicode[STIX]{x1D703}=59.50^{\circ }$
. As shown in Figure 4(b), a mid-IR idler pulse with a spectral range covering
$\unicode[STIX]{x1D703}=59.50^{\circ }$
. As shown in Figure 4(b), a mid-IR idler pulse with a spectral range covering
![]() $4.5$
–
$4.5$
–
![]() $6.5~\unicode[STIX]{x03BC}\text{m}$
can be achieved by the DFG between different pairs of the pump and signal components.
$6.5~\unicode[STIX]{x03BC}\text{m}$
can be achieved by the DFG between different pairs of the pump and signal components.
In addition to broadband PM for the
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
idler, the intrapulse DFG can automatically stabilize the CEP of the mid-IR pulses. The phases of the three interacting waves in DFG satisfy the relation,
$5.2~\unicode[STIX]{x03BC}\text{m}$
idler, the intrapulse DFG can automatically stabilize the CEP of the mid-IR pulses. The phases of the three interacting waves in DFG satisfy the relation,
![]() $\unicode[STIX]{x1D719}_{i}=\unicode[STIX]{x1D719}_{p}-\unicode[STIX]{x1D719}_{s}-\unicode[STIX]{x1D70B}/2$
[Reference Baltuška, Fuji and Kobayashi52]. As the pump and signal incidence share the same CEP, the CEP fluctuations
$\unicode[STIX]{x1D719}_{i}=\unicode[STIX]{x1D719}_{p}-\unicode[STIX]{x1D719}_{s}-\unicode[STIX]{x1D70B}/2$
[Reference Baltuška, Fuji and Kobayashi52]. As the pump and signal incidence share the same CEP, the CEP fluctuations
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D719}$
due to mechanical instabilities or air turbulence are automatically canceled in the mid-IR idler phase, as schematically plotted in Figure 5(a). Such a passive CEP stabilization does not require any electronic feedback circuits. Moreover, the synchronization between the pump and signal components can be achieved by controlling GDD of the input octave-spanning pulse through optimizing the compressor in the Ti:sapphire laser.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D719}$
due to mechanical instabilities or air turbulence are automatically canceled in the mid-IR idler phase, as schematically plotted in Figure 5(a). Such a passive CEP stabilization does not require any electronic feedback circuits. Moreover, the synchronization between the pump and signal components can be achieved by controlling GDD of the input octave-spanning pulse through optimizing the compressor in the Ti:sapphire laser.
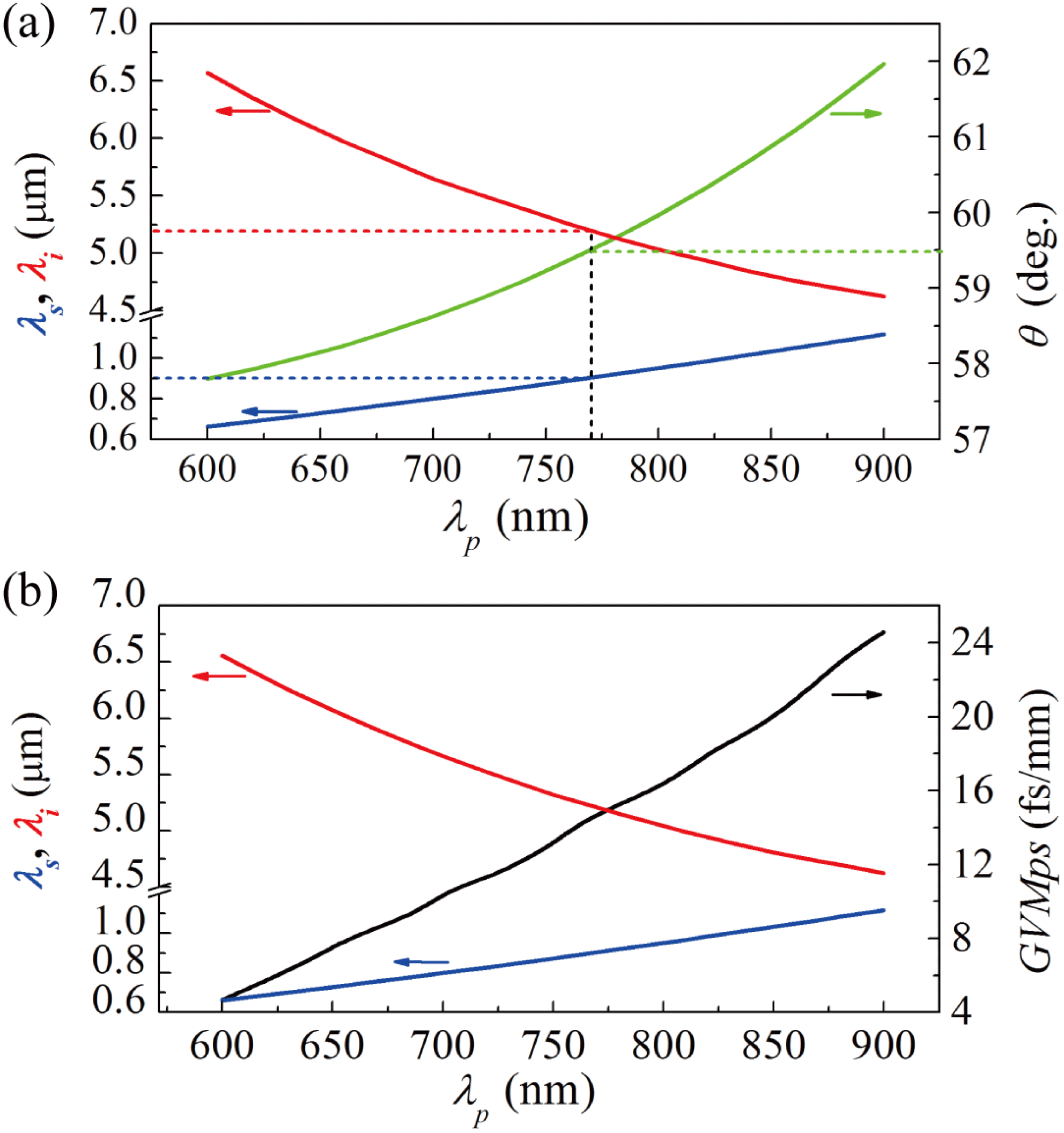
Figure 4. PM properties of Type-II collinear intrapulse DFG. (a) The attainable signal (blue) and idler (red) wavelengths under the condition of
![]() $\text{GVM}_{si}=0$
. In the calculation, the PM angle
$\text{GVM}_{si}=0$
. In the calculation, the PM angle
![]() $\unicode[STIX]{x1D703}$
(green) is varied with the pump wavelength. (b) The phase-matched signal (blue) wavelength, idler (red) wavelength and the corresponding
$\unicode[STIX]{x1D703}$
(green) is varied with the pump wavelength. (b) The phase-matched signal (blue) wavelength, idler (red) wavelength and the corresponding
![]() $\text{GVM}_{ps}$
(black) at
$\text{GVM}_{ps}$
(black) at
![]() $\unicode[STIX]{x1D703}=59.50^{\circ }$
.
$\unicode[STIX]{x1D703}=59.50^{\circ }$
.
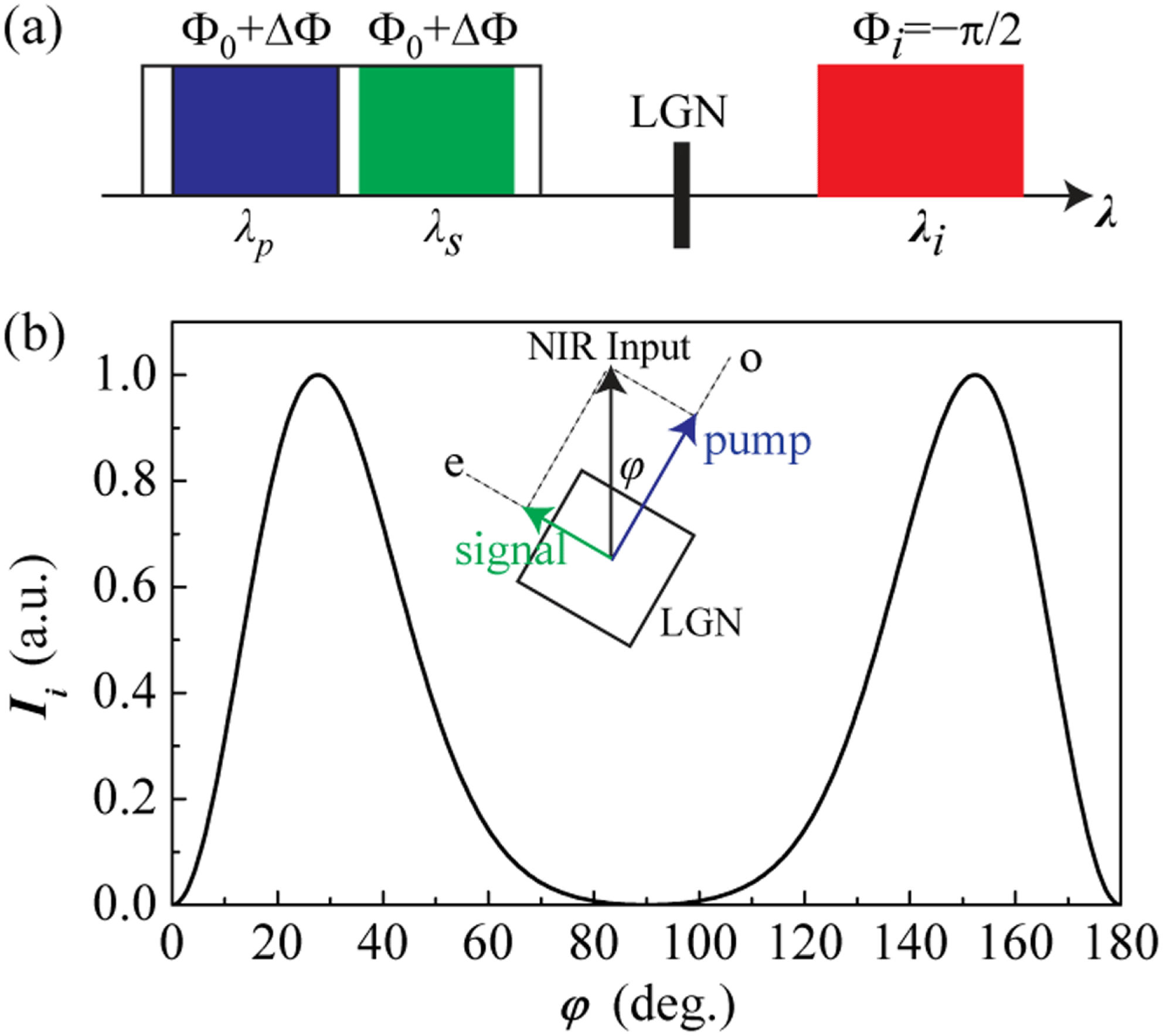
Figure 5. (a) Schematic of intrapulse DFG for passive CEP stability. (b) Calculated mid-IR idler intensity as a function of the polarization angle
![]() $\unicode[STIX]{x1D711}$
. The inset in (b) illustrates the definition of the angle
$\unicode[STIX]{x1D711}$
. The inset in (b) illustrates the definition of the angle
![]() $\unicode[STIX]{x1D711}$
. The calculation parameters are
$\unicode[STIX]{x1D711}$
. The calculation parameters are
![]() $\unicode[STIX]{x1D706}_{p}=770~\text{nm}$
,
$\unicode[STIX]{x1D706}_{p}=770~\text{nm}$
,
![]() $\unicode[STIX]{x1D706}_{s}=904~\text{nm}$
,
$\unicode[STIX]{x1D706}_{s}=904~\text{nm}$
,
![]() $\unicode[STIX]{x1D706}_{i}=5.2~\unicode[STIX]{x03BC}\text{m}$
,
$\unicode[STIX]{x1D706}_{i}=5.2~\unicode[STIX]{x03BC}\text{m}$
,
![]() $\unicode[STIX]{x1D703}=59.50^{\circ }$
,
$\unicode[STIX]{x1D703}=59.50^{\circ }$
,
![]() $L=0.1~\text{mm}$
and
$L=0.1~\text{mm}$
and
![]() $I_{0}=1~\text{TW}/\text{cm}^{2}$
.
$I_{0}=1~\text{TW}/\text{cm}^{2}$
.
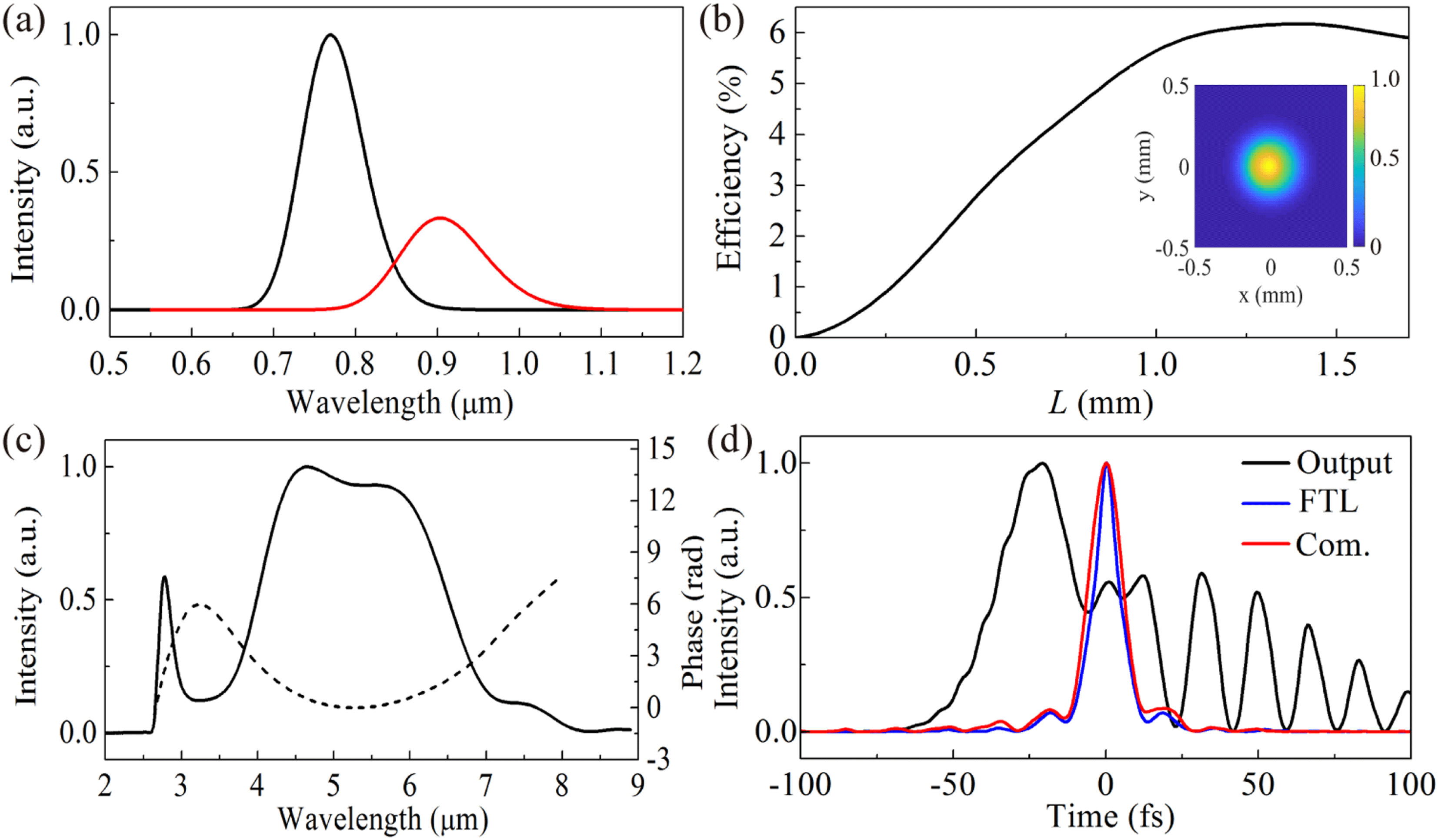
Figure 6. Simulation results for intrapulse DFG. (a) Input pump (black) and signal (red) spectral components. (b) Idler efficiency versus LGN crystal length. Inset shows the idler beam profile at
![]() $L=0.7~\text{mm}$
. (c) Output mid-IR idler spectrum (solid) and phase (dashed) at
$L=0.7~\text{mm}$
. (c) Output mid-IR idler spectrum (solid) and phase (dashed) at
![]() $L=0.7~\text{mm}$
. (d) Output idler pulse before (black) and after (red) dispersion compensation with GDD of
$L=0.7~\text{mm}$
. (d) Output idler pulse before (black) and after (red) dispersion compensation with GDD of
![]() $652~\text{fs}^{2}$
and TOD of
$652~\text{fs}^{2}$
and TOD of
![]() $-5.84\times 10^{3}~\text{fs}^{3}$
. The blue curve shows the FTL pulse. The parameters used in the simulation are
$-5.84\times 10^{3}~\text{fs}^{3}$
. The blue curve shows the FTL pulse. The parameters used in the simulation are
![]() $\unicode[STIX]{x1D706}_{p}=770~\text{nm}$
,
$\unicode[STIX]{x1D706}_{p}=770~\text{nm}$
,
![]() $\unicode[STIX]{x1D706}_{s}=904~\text{nm}$
,
$\unicode[STIX]{x1D706}_{s}=904~\text{nm}$
,
![]() $\unicode[STIX]{x1D706}_{i}=5.2~\unicode[STIX]{x03BC}\text{m}$
,
$\unicode[STIX]{x1D706}_{i}=5.2~\unicode[STIX]{x03BC}\text{m}$
,
![]() $\unicode[STIX]{x1D703}=59.50^{\circ }$
,
$\unicode[STIX]{x1D703}=59.50^{\circ }$
,
![]() $I_{p0}=0.75~\text{TW}/\text{cm}^{2}$
and
$I_{p0}=0.75~\text{TW}/\text{cm}^{2}$
and
![]() $I_{s0}=0.25~\text{TW}/\text{cm}^{2}$
.
$I_{s0}=0.25~\text{TW}/\text{cm}^{2}$
.
Figure 7. Simulation results for the three-stage OPCPA. (a) Evolution of the mid-IR pulse energy in the first (green), second (red) and third (blue) OPCPA stages. (b) Evolution of chirped mid-IR pulse duration with amplification. The black curve represents the input chirped pulse. (c) Evolution of mid-IR spectrum with amplification. The black curve represents the input mid-IR spectrum. (d) FTL pulses after OPCPA-3 (blue) and seed mid-IR pulses before stretching (black). (e) Pump beam profile output from the first (left), second (middle) and third (right) OPCPA stages. (f) Mid-IR beam profile output from the first (left), second (middle) and third (right) OPCPA stages.
To accommodate Type-II DFG, the LGN crystal is rotated around the light path so that the linearly polarized input beam can have components along the
![]() $o$
-wave and
$o$
-wave and
![]() $e$
-wave directions of the crystal (inset in Figure 5(b)). At a fixed input intensity
$e$
-wave directions of the crystal (inset in Figure 5(b)). At a fixed input intensity
![]() $I_{0}$
, the pump and signal intensities are determined by
$I_{0}$
, the pump and signal intensities are determined by
![]() $I_{p0}=I_{0}\cos ^{2}\unicode[STIX]{x1D711}$
and
$I_{p0}=I_{0}\cos ^{2}\unicode[STIX]{x1D711}$
and
![]() $I_{s0}=I_{0}\sin ^{2}\unicode[STIX]{x1D711}$
, respectively, where
$I_{s0}=I_{0}\sin ^{2}\unicode[STIX]{x1D711}$
, respectively, where
![]() $\unicode[STIX]{x1D711}$
is the angle between the beam polarization and the
$\unicode[STIX]{x1D711}$
is the angle between the beam polarization and the
![]() $o$
-wave of the crystal. With a perfect PM (
$o$
-wave of the crystal. With a perfect PM (
![]() $\unicode[STIX]{x0394}k=0$
), the mid-IR idler intensity in the small-signal regime is given by[Reference Cerullo and Silvestri58]
$\unicode[STIX]{x0394}k=0$
), the mid-IR idler intensity in the small-signal regime is given by[Reference Cerullo and Silvestri58]
where
![]() $\unicode[STIX]{x1D6E4}=2\unicode[STIX]{x1D714}_{s}\unicode[STIX]{x1D714}_{i}d_{\text{eff}}^{2}I_{p0}/(n_{p}n_{s}n_{i}\unicode[STIX]{x1D700}_{0}c_{0}^{3})$
. Equation (6) suggests a
$\unicode[STIX]{x1D6E4}=2\unicode[STIX]{x1D714}_{s}\unicode[STIX]{x1D714}_{i}d_{\text{eff}}^{2}I_{p0}/(n_{p}n_{s}n_{i}\unicode[STIX]{x1D700}_{0}c_{0}^{3})$
. Equation (6) suggests a
![]() $\unicode[STIX]{x1D711}$
-dependent idler intensity. To achieve the strongest idler, we study the idler intensity as a function of
$\unicode[STIX]{x1D711}$
-dependent idler intensity. To achieve the strongest idler, we study the idler intensity as a function of
![]() $\unicode[STIX]{x1D711}$
with
$\unicode[STIX]{x1D711}$
with
![]() $I_{0}=1~\text{TW}/\text{cm}^{2}$
, as shown in Figure 5(b). The calculation shows that the idler is maximum at
$I_{0}=1~\text{TW}/\text{cm}^{2}$
, as shown in Figure 5(b). The calculation shows that the idler is maximum at
![]() $\unicode[STIX]{x1D711}=30^{\circ }$
or
$\unicode[STIX]{x1D711}=30^{\circ }$
or
![]() $150^{\circ }$
. These two polarization angles correspond to the pump and signal intensities of
$150^{\circ }$
. These two polarization angles correspond to the pump and signal intensities of
![]() $I_{p0}=0.75I_{0}$
and
$I_{p0}=0.75I_{0}$
and
![]() $I_{s0}=0.25I_{0}$
.
$I_{s0}=0.25I_{0}$
.
Based on the above parameters and analysis, we numerically solve Equations (3)–(5) to verify the performance of intrapulse DFG. In a real intrapulse DFG experiment, it is difficult to distinguish the signal from the pump because their spectra are the same. However, Figure 4(b) shows that the spectral components participating in the DFG process are different for the pump and signal. To facilitate simulations, we allocate different spectrum coverage for the pump pulse centered at 770 nm and the signal pulse centered at 904 nm, as shown in Figure 6(a). The pump and signal pulses are assumed to have Gaussian profiles in both temporal and spatial domains, which share the same temporal width of 10 fs and the same beam width of
![]() $350~\unicode[STIX]{x03BC}\text{m}$
(FWHM). With
$350~\unicode[STIX]{x03BC}\text{m}$
(FWHM). With
![]() $I_{p0}=0.75~\text{TW}/\text{cm}^{2}$
and
$I_{p0}=0.75~\text{TW}/\text{cm}^{2}$
and
![]() $I_{s0}=0.25~\text{TW}/\text{cm}^{2}$
, the evolution of the generated idler intensity with the LGN length
$I_{s0}=0.25~\text{TW}/\text{cm}^{2}$
, the evolution of the generated idler intensity with the LGN length
![]() $L$
is shown in Figure 6(b), which indicates that the idler is maximum at
$L$
is shown in Figure 6(b), which indicates that the idler is maximum at
![]() $L=1.4~\text{mm}$
with a conversion efficiency of
$L=1.4~\text{mm}$
with a conversion efficiency of
![]() ${\sim}6\%$
. As the group-velocity mismatch between the pump and signal components (
${\sim}6\%$
. As the group-velocity mismatch between the pump and signal components (
![]() $\text{GVM}_{ps}$
) is about
$\text{GVM}_{ps}$
) is about
![]() $15~\text{fs}/\text{mm}$
as given in Figure 4(b), the crystal length is limited to
$15~\text{fs}/\text{mm}$
as given in Figure 4(b), the crystal length is limited to
![]() $L=0.7~\text{mm}$
in our simulations for ensuring a good overlap between the 10 fs interacting pulses. In this case, a mid-IR idler pulse with good spatial (inset in Figure 6(b)) and spectral profiles could be obtained (black solid curve in Figure 6(c)).
$L=0.7~\text{mm}$
in our simulations for ensuring a good overlap between the 10 fs interacting pulses. In this case, a mid-IR idler pulse with good spatial (inset in Figure 6(b)) and spectral profiles could be obtained (black solid curve in Figure 6(c)).
Figure 6(b) shows a conversion efficiency of about 4.2% at
![]() $L=0.7~\text{mm}$
. When using a
$L=0.7~\text{mm}$
. When using a
![]() $15~\unicode[STIX]{x03BC}\text{J}$
octave-spanning pulse to pump the Type-II intrapulse DFG in LGN, the attainable mid-IR pulse energy is
$15~\unicode[STIX]{x03BC}\text{J}$
octave-spanning pulse to pump the Type-II intrapulse DFG in LGN, the attainable mid-IR pulse energy is
![]() ${\sim}630~\text{nJ}$
. The output mid-IR spectrum at
${\sim}630~\text{nJ}$
. The output mid-IR spectrum at
![]() $L=0.7~\text{mm}$
is shown in Figure 6(c), which agrees with the calculated spectrum coverage in Figure 4(b) but presents a dip at the center. This dip results from the change of PM condition caused by
$L=0.7~\text{mm}$
is shown in Figure 6(c), which agrees with the calculated spectrum coverage in Figure 4(b) but presents a dip at the center. This dip results from the change of PM condition caused by
![]() $n_{2}$
. Since the PM is dominant by GVD, the
$n_{2}$
. Since the PM is dominant by GVD, the
![]() $n_{2}$
-induced refractive-index change will shift the perfect PM wavelength from the center to two side wavelengths and, hence, cause the dip on the spectrum. The broad idler spectrum supports a Fourier transform-limited (FTL) pulse duration of
$n_{2}$
-induced refractive-index change will shift the perfect PM wavelength from the center to two side wavelengths and, hence, cause the dip on the spectrum. The broad idler spectrum supports a Fourier transform-limited (FTL) pulse duration of
![]() ${\sim}12.5~\text{fs}$
in FWHM (blue curve in Figure 6(d)). However, the practical output pulse from intrapulse DFG deviates from the FTL pulse largely (black curve in Figure 6(d)), which is a result of dispersion effect. As shown by the black dashed curve in Figure 6(c), the spectral phase is dominant by GVD and TOD. After compensating the spectral phase with GDD of
${\sim}12.5~\text{fs}$
in FWHM (blue curve in Figure 6(d)). However, the practical output pulse from intrapulse DFG deviates from the FTL pulse largely (black curve in Figure 6(d)), which is a result of dispersion effect. As shown by the black dashed curve in Figure 6(c), the spectral phase is dominant by GVD and TOD. After compensating the spectral phase with GDD of
![]() $652~\text{fs}^{2}$
and TOD of
$652~\text{fs}^{2}$
and TOD of
![]() $-5.84\times 10^{3}~\text{fs}^{3}$
, a mid-IR pulse with an FWHM duration of
$-5.84\times 10^{3}~\text{fs}^{3}$
, a mid-IR pulse with an FWHM duration of
![]() ${\sim}13.0~\text{fs}$
can be obtained, corresponding to less than one optical cycle at
${\sim}13.0~\text{fs}$
can be obtained, corresponding to less than one optical cycle at
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
.
$5.2~\unicode[STIX]{x03BC}\text{m}$
.
4.2 Three-stage OPCPA
Spectral width of the
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
mid-IR pulse output from the intrapulse DFG stage (
$5.2~\unicode[STIX]{x03BC}\text{m}$
mid-IR pulse output from the intrapulse DFG stage (
![]() $L=0.7~\text{mm}$
) exceeds the gain bandwidth of OPCPA. To facilitate OPCPA simulations, here, we simplify the spectrum shown in Figure 6(c) into a Gaussian spectrum with an FWHM bandwidth of
$L=0.7~\text{mm}$
) exceeds the gain bandwidth of OPCPA. To facilitate OPCPA simulations, here, we simplify the spectrum shown in Figure 6(c) into a Gaussian spectrum with an FWHM bandwidth of
![]() $1~\unicode[STIX]{x03BC}\text{m}$
(black curve in Figure 7(c)). The Gaussian-profile mid-IR pulses are stretched into 2.0 ps by a mid-IR AOPDF before entering OPCPA for further amplification. The matched pulse durations between pump light and mid-IR light can suppress the effect of parametric fluorescence on CEP stability although it may result in a sacrifice in amplification bandwidth[Reference Moses, Huang, Hong, Mücke, Falcão-Filho, Benedick, Ilday, Dergachev, Bolger, Eggleton and Kärtner59]. With an AOPDF diffraction efficiency of 15%, the pulse is expected to have an energy of 90 nJ for seeding OPCPA. With the available pump energy of 200 mJ, we estimate that the 90 nJ mid-IR seed can be amplified to
$1~\unicode[STIX]{x03BC}\text{m}$
(black curve in Figure 7(c)). The Gaussian-profile mid-IR pulses are stretched into 2.0 ps by a mid-IR AOPDF before entering OPCPA for further amplification. The matched pulse durations between pump light and mid-IR light can suppress the effect of parametric fluorescence on CEP stability although it may result in a sacrifice in amplification bandwidth[Reference Moses, Huang, Hong, Mücke, Falcão-Filho, Benedick, Ilday, Dergachev, Bolger, Eggleton and Kärtner59]. With an AOPDF diffraction efficiency of 15%, the pulse is expected to have an energy of 90 nJ for seeding OPCPA. With the available pump energy of 200 mJ, we estimate that the 90 nJ mid-IR seed can be amplified to
![]() ${\sim}20~\text{mJ}$
with a total gain of approximately
${\sim}20~\text{mJ}$
with a total gain of approximately
![]() $2\times 10^{5}$
. Although such a gain level can be provided by a single OPCPA stage, three stages are used to lower the small-signal gain in each stage. This arrangement benefits the suppression of optical parametric fluorescence, and thereby helps improve the stabilities of both output energy and CEP.
$2\times 10^{5}$
. Although such a gain level can be provided by a single OPCPA stage, three stages are used to lower the small-signal gain in each stage. This arrangement benefits the suppression of optical parametric fluorescence, and thereby helps improve the stabilities of both output energy and CEP.
The design parameters of the three-stage OPCPA are given in Figure 3. Three OPCPA stages are successively pumped by 5, 45 and 150 mJ of 1030 nm Yb:YAG laser with spatiotemporally Gaussian profiles. The pulse durations of pump pulses are 2 ps (FWHM), and the beam widths of pump are set as 2.1, 6.1 and 11.2 mm (FWHM), respectively, rendering a same pump intensity of
![]() $50~\text{GW}/\text{cm}^{2}$
for three stages. The damage threshold of LGN crystal has been measured to be
$50~\text{GW}/\text{cm}^{2}$
for three stages. The damage threshold of LGN crystal has been measured to be
![]() ${\sim}1.41~\text{GW}/\text{cm}^{2}$
pumped by a 10 ns laser[Reference Lu, Xu, Yu, Fu, Zhang, Segonds, Boulanger, Zhang and Wang48]. Since the damage threshold increases with the shortening of pulse duration
${\sim}1.41~\text{GW}/\text{cm}^{2}$
pumped by a 10 ns laser[Reference Lu, Xu, Yu, Fu, Zhang, Segonds, Boulanger, Zhang and Wang48]. Since the damage threshold increases with the shortening of pulse duration
![]() $\unicode[STIX]{x1D70F}$
by a
$\unicode[STIX]{x1D70F}$
by a
![]() $\unicode[STIX]{x1D70F}^{-1/2}$
scaling law[Reference Stuart, Feit, Rubenchik, Shore and Perry53], we can expect a damage threshold of approaching
$\unicode[STIX]{x1D70F}^{-1/2}$
scaling law[Reference Stuart, Feit, Rubenchik, Shore and Perry53], we can expect a damage threshold of approaching
![]() $100~\text{GW}/\text{cm}^{2}$
for the LGN crystal at a pulse duration of 2 ps. Therefore, the adopted pump intensity of
$100~\text{GW}/\text{cm}^{2}$
for the LGN crystal at a pulse duration of 2 ps. Therefore, the adopted pump intensity of
![]() $50~\text{GW}/\text{cm}^{2}$
in our simulations is well below the damage threshold of the LGN crystal. The mid-IR beam is assumed to have the same beam size as that of pump beam in each OPCPA stage for ensuring a sufficient spatial overlap between pump and mid-IR beams, so beam telescopes for mid-IR pulses are added before each stage in our simulation. The apertures of both LGN crystals are assumed to be 30 mm, which is much smaller than the currently available maximum aperture of 4 inches[Reference Boursier, Segonds, Boulanger, Félix, Debray, Jegouso, Ménaert, Roshchupkin and Shoji49]. The Type-II noncollinear PM (i.e.,
$50~\text{GW}/\text{cm}^{2}$
in our simulations is well below the damage threshold of the LGN crystal. The mid-IR beam is assumed to have the same beam size as that of pump beam in each OPCPA stage for ensuring a sufficient spatial overlap between pump and mid-IR beams, so beam telescopes for mid-IR pulses are added before each stage in our simulation. The apertures of both LGN crystals are assumed to be 30 mm, which is much smaller than the currently available maximum aperture of 4 inches[Reference Boursier, Segonds, Boulanger, Félix, Debray, Jegouso, Ménaert, Roshchupkin and Shoji49]. The Type-II noncollinear PM (i.e.,
![]() $1030~\text{nm}(o)\rightarrow 5.2~\unicode[STIX]{x03BC}\text{m}(o)+1284~\text{nm}(e)$
) is adopted in the simulations of OPCPA. The noncollinear angle
$1030~\text{nm}(o)\rightarrow 5.2~\unicode[STIX]{x03BC}\text{m}(o)+1284~\text{nm}(e)$
) is adopted in the simulations of OPCPA. The noncollinear angle
![]() $\unicode[STIX]{x1D6FC}$
between the pump and mid-IR beams is
$\unicode[STIX]{x1D6FC}$
between the pump and mid-IR beams is
![]() $5.95^{\circ }$
inside the crystal, while the PM angle
$5.95^{\circ }$
inside the crystal, while the PM angle
![]() $\unicode[STIX]{x1D703}$
is
$\unicode[STIX]{x1D703}$
is
![]() $76^{\circ }$
. Based on these parameter settings, we perform numerical simulations for the three-stage OPCPA system and summarize the results in Figure 7.
$76^{\circ }$
. Based on these parameter settings, we perform numerical simulations for the three-stage OPCPA system and summarize the results in Figure 7.
Three OPCPA stages, based on LGN crystals with lengths of 15, 12 and 7 mm, respectively, amplify the 90 nJ mid-IR seed to 0.1, 2.8 and 16.5 mJ successively, with the total pump-to-IR energy conversion efficiency of about 8% (Figure 7(a)). All three stages work in the saturation amplification regime, as indicated by the depletion on the pump beam profiles after each stage (Figure 7(e)). The OPCPA-2 is slightly over saturation to maximize the energy extraction in the OPCPA-3, so there is a dip at the center of the mid-IR beam (middle panel in Figure 7(f)). This dip disappears on the mid-IR beam profile after OPCPA-3 (right panel in Figure 7(f)). Figures 7(b) and 7(c) show the evolutions of mid-IR chirped-pulse duration and spectrum, respectively. Despite a 2 ps seeding, the mid-IR chirped pulse narrows down to about 1 ps after OPCPA-1 (green curve in Figure 7(b)) because the gain bandwidth is narrower than the seeding bandwidth (green curve in Figure 7(c)). The mid-IR pulse spectrum after OPCPA-1 is sufficiently amplified by following two stages without suffering from gain-narrowing. The dip on the spectrum from OPCPA-2 is a result of deep saturation amplification, where back conversion occurs at the center of the spectrum (red curve in Figure 7(c)). This spectrum dip is filled moderately by OPCPA-3 (blue curve in Figure 7(c)). It is interesting to observe the evolution of pulse duration in OPCPA-2 and OPCPA-3, which becomes longer with amplification (red and blue curves in Figure 7(b)). Such a duration broadening, induced by the large dispersion in LGN crystal (
![]() $-1.34\times 10^{3}~\text{fs}^{2}/\text{mm}$
), ensures sufficient overlap between pump and mid-IR pulses and thereby enables effective energy extraction from the 2 ps pump pulses. The seed spectral components are finally amplified with a bandwidth of
$-1.34\times 10^{3}~\text{fs}^{2}/\text{mm}$
), ensures sufficient overlap between pump and mid-IR pulses and thereby enables effective energy extraction from the 2 ps pump pulses. The seed spectral components are finally amplified with a bandwidth of
![]() ${\sim}0.5~\unicode[STIX]{x03BC}\text{m}$
around
${\sim}0.5~\unicode[STIX]{x03BC}\text{m}$
around
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
after OPCPA-3. After compression, the amplified mid-IR spectrum can support an FTL pulse duration of 120 fs, corresponding to seven optical cycles at a wavelength of
$5.2~\unicode[STIX]{x03BC}\text{m}$
after OPCPA-3. After compression, the amplified mid-IR spectrum can support an FTL pulse duration of 120 fs, corresponding to seven optical cycles at a wavelength of
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
(blue curve in Figure 7(d)). The peak power of the compressed mid-IR pulse can finally reach 0.13 TW.
$5.2~\unicode[STIX]{x03BC}\text{m}$
(blue curve in Figure 7(d)). The peak power of the compressed mid-IR pulse can finally reach 0.13 TW.
Table 3. Optical parameters at
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
of six commonly used bulk materials.
$5.2~\unicode[STIX]{x03BC}\text{m}$
of six commonly used bulk materials.
4.3 Dispersion management
The use of a picosecond pump pulse facilitates the compression of a
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
pulse by bulk materials. Several key factors should be considered in the selection of bulk compression materials, including the transparent range, the magnitude and sign of the GVD and the magnitude of the nonlinear refractive index
$5.2~\unicode[STIX]{x03BC}\text{m}$
pulse by bulk materials. Several key factors should be considered in the selection of bulk compression materials, including the transparent range, the magnitude and sign of the GVD and the magnitude of the nonlinear refractive index
![]() $n_{2}$
. As the amplified mid-IR pulse is negatively chirped, a material with both a large positive GVD and a small
$n_{2}$
. As the amplified mid-IR pulse is negatively chirped, a material with both a large positive GVD and a small
![]() $n_{2}$
is more desirable for pulse compression to have sufficient dispersion without a significant nonlinear phase shift.
$n_{2}$
is more desirable for pulse compression to have sufficient dispersion without a significant nonlinear phase shift.
Table 3 summarizes the relevant optical parameters of several commonly used bulk materials at
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
, including silicon (Si), germanium (Ge), barium fluoride (
$5.2~\unicode[STIX]{x03BC}\text{m}$
, including silicon (Si), germanium (Ge), barium fluoride (
![]() $\text{BaF}_{2}$
), calcium fluoride (
$\text{BaF}_{2}$
), calcium fluoride (
![]() $\text{CaF}_{2}$
), zinc selenide (ZnSe) and sodium chloride (NaCl), all of which are transparent for the spectral range of
$\text{CaF}_{2}$
), zinc selenide (ZnSe) and sodium chloride (NaCl), all of which are transparent for the spectral range of
![]() $4.5{-}6.5~\unicode[STIX]{x03BC}\text{m}$
. Obviously, only Si and Ge meet the compression requirement of a positive GVD at
$4.5{-}6.5~\unicode[STIX]{x03BC}\text{m}$
. Obviously, only Si and Ge meet the compression requirement of a positive GVD at
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
. We note that these two materials have a large refractive index
$5.2~\unicode[STIX]{x03BC}\text{m}$
. We note that these two materials have a large refractive index
![]() $n$
and a nonlinear refractive index
$n$
and a nonlinear refractive index
![]() $n_{2}$
, which may be unfavorable in practical applications. The large value of
$n_{2}$
, which may be unfavorable in practical applications. The large value of
![]() $n$
can increase the energy loss due to Fresnel reflections, so the surfaces should be antireflection coated or cut at Brewster angle. The effect of
$n$
can increase the energy loss due to Fresnel reflections, so the surfaces should be antireflection coated or cut at Brewster angle. The effect of
![]() $n_{2}$
can be measured by the
$n_{2}$
can be measured by the
![]() $B$
integral (the accumulated nonlinear phase in the material),
$B$
integral (the accumulated nonlinear phase in the material),
![]() $B=2\unicode[STIX]{x1D70B}n_{2}IL/\unicode[STIX]{x1D706}$
, which should be below
$B=2\unicode[STIX]{x1D70B}n_{2}IL/\unicode[STIX]{x1D706}$
, which should be below
![]() $\unicode[STIX]{x1D70B}$
to avoid pulse distortion. Because both the GDD and
$\unicode[STIX]{x1D70B}$
to avoid pulse distortion. Because both the GDD and
![]() $B$
integral depend on the material thickness
$B$
integral depend on the material thickness
![]() $L$
, we evaluate Si and Ge by comparing the figure of merit
$L$
, we evaluate Si and Ge by comparing the figure of merit
![]() $\text{GVD}/n_{2}$
. Si with a larger value of
$\text{GVD}/n_{2}$
. Si with a larger value of
![]() $\text{GVD}/n_{2}$
is more suitable for use as the compression material. Moreover, Si has a relatively smaller
$\text{GVD}/n_{2}$
is more suitable for use as the compression material. Moreover, Si has a relatively smaller
![]() $n$
and TOD than Ge.
$n$
and TOD than Ge.
The required length of Si is determined by the total negative dispersion experienced by the mid-IR chirped pulse. We calculate the GDD and TOD induced in the stretching and amplification processes. A 187.1 mm long Si plate is needed to fully compensate the negative GDD imposed by the AOPDF and three LGN crystals. As both the Si plate and LGN crystal have positive TOD, they can impose a total TOD of
![]() $5.68\times 10^{5}~\text{fs}^{3}$
on the chirped pulse. This amount of TOD can be compensated by the AOPDF (e.g., Fastlite DAZZLER UWB-3500-7000) inserted before the first OPCPA stage. The AOPDF combines the roles of pulse stretching and high-order dispersion compensation. The detailed dispersion management is listed in Table 4, where air dispersion for
$5.68\times 10^{5}~\text{fs}^{3}$
on the chirped pulse. This amount of TOD can be compensated by the AOPDF (e.g., Fastlite DAZZLER UWB-3500-7000) inserted before the first OPCPA stage. The AOPDF combines the roles of pulse stretching and high-order dispersion compensation. The detailed dispersion management is listed in Table 4, where air dispersion for
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
pulses is neglected.
$5.2~\unicode[STIX]{x03BC}\text{m}$
pulses is neglected.
Table 4. Dispersion management for the
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
OPCPA.
$5.2~\unicode[STIX]{x03BC}\text{m}$
OPCPA.

The 16.5 mJ amplified mid-IR pulse before and after compression by the Si block has peak powers of 7.9 and 137.5 GW, respectively. The averaged peak power in the Si block is approximately 72.7 GW. To control the total
![]() $B$
integral to be below
$B$
integral to be below
![]() $\unicode[STIX]{x1D70B}$
, the beam diameter (full width at
$\unicode[STIX]{x1D70B}$
, the beam diameter (full width at
![]() $1/e^{2}$
maximum) of the mid-IR pulse in the Si block should be larger than 134 mm. To avoid beam clipping, it is necessary to use a Si block with a diameter of
$1/e^{2}$
maximum) of the mid-IR pulse in the Si block should be larger than 134 mm. To avoid beam clipping, it is necessary to use a Si block with a diameter of
![]() ${\sim}150~\text{mm}$
. Such a large-size Si-compressor is commercially available because the 300 mm diameter Si crystal has been a standard product currently.
${\sim}150~\text{mm}$
. Such a large-size Si-compressor is commercially available because the 300 mm diameter Si crystal has been a standard product currently.
4.4 Performance scalability
We have numerically demonstrated the generation of
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
, 0.13 TW, seven-cycle pulses by employing the LGN crystal, which exhibits the potential and prospects of langasite oxides in mid-IR applications. However, it is difficult for the LGN crystal to generate mid-IR pulses beyond
$5.2~\unicode[STIX]{x03BC}\text{m}$
, 0.13 TW, seven-cycle pulses by employing the LGN crystal, which exhibits the potential and prospects of langasite oxides in mid-IR applications. However, it is difficult for the LGN crystal to generate mid-IR pulses beyond
![]() $7~\unicode[STIX]{x03BC}\text{m}$
due to its limited transparent range, as shown in Figure 1. The recently proposed langasite oxide
$7~\unicode[STIX]{x03BC}\text{m}$
due to its limited transparent range, as shown in Figure 1. The recently proposed langasite oxide
![]() $\text{La}_{3}\text{SnGa}_{5}\text{O}_{14}$
(LGSn), a new kind of oxide crystal, has a much broader transparent range from
$\text{La}_{3}\text{SnGa}_{5}\text{O}_{14}$
(LGSn), a new kind of oxide crystal, has a much broader transparent range from
![]() $0.27$
to
$0.27$
to
![]() $11~\unicode[STIX]{x03BC}\text{m}$
[Reference Lan, Liang, Jiang, Zhang, Yu, Liu, Zhang, Wang and Wu51]. The LGSn crystal may provide a solution to generate intense long-wavelength IR pulses beyond
$11~\unicode[STIX]{x03BC}\text{m}$
[Reference Lan, Liang, Jiang, Zhang, Yu, Liu, Zhang, Wang and Wu51]. The LGSn crystal may provide a solution to generate intense long-wavelength IR pulses beyond
![]() $10~\unicode[STIX]{x03BC}\text{m}$
by using pure oxide crystals and traditional near-IR pump sources.
$10~\unicode[STIX]{x03BC}\text{m}$
by using pure oxide crystals and traditional near-IR pump sources.
The seven-cycle mid-IR pulses from OPCPA can be further compressed down to sub-three-cycle or even sub-cycle pulses by nonlinear compression methods. Filamentation-assisted supercontinuum generation followed by anomalous dispersion compensation has been used to nonlinearly compress the mid-IR pulse[Reference Elu, Baudisch, Pires, Tani, Frosz, Köttig, Ermolov, Russell and Biegert35, Reference Mitrofanov, Voronin, Sidorov-Biryukov, Mitryukovsky, Fedotov, Serebryannikov, Meshchankin, Shumakova, Ališauskas, Pugžlys, Panchenko, Baltuška and Zheltikov60]. Recently, supercontinuum generation and self-compression in bulks have attracted much attention due to good shot-to-shot repeatability and the absence of complicated pulse splitting[Reference Silva, Austin, Thai, Baudisch, Hemmer, Faccio, Couairon and Biegert61, Reference Shumakova, Malevich, Ališauska, Voronin, Zheltikov, Faccio, Kartashov, Baltuška and Pugžlys62]. In addition, nonlinear soliton compression via quadratic cascaded nonlinearity is another potential route to compress mid-IR pulses with good controllability[Reference Liu, Qian and Wise63, Reference Bache, Guo and Zhou64]. All these nonlinear compression methods usually have a high efficiency of
![]() ${\sim}50\%$
, so the peak power of the pulse will be enhanced if the compression ratio is higher than two.
${\sim}50\%$
, so the peak power of the pulse will be enhanced if the compression ratio is higher than two.
In addition to pulse shortening by nonlinear compression, the scaling of the peak power of mid-IR OPCPA ultimately relies on the available pump energy. The pulse energy of a commercial Yb:YAG thin-disk regenerative laser is currently a maximum of 200 mJ in the design, which may be further boosted up to Joule-level energy at the expense of cost[Reference Reagan, Baumgarten, Jankowska, Chi, Bravo, Dehne, Pedicone, Yin, Wang, Menoni and Rocca65]. With the development of a Joule-level, kHz, picosecond Yb:YAG thin-disk laser, OPCPA based on large-size langasite oxide crystals can support
![]() ${\sim}1~\text{TW}$
few-cycle pulses at
${\sim}1~\text{TW}$
few-cycle pulses at
![]() $5{-}10~\unicode[STIX]{x03BC}\text{m}$
. On the other hand, the needed size of Si-compressor should be increased accordingly. With the development of growth technology, a Si crystal with diameters up to 450 mm (and potentially 675 mm) can be supported[Reference Lu and Kimbel66], which can serve as the compressor for the TW-class mid-IR OPCPA systems.
$5{-}10~\unicode[STIX]{x03BC}\text{m}$
. On the other hand, the needed size of Si-compressor should be increased accordingly. With the development of growth technology, a Si crystal with diameters up to 450 mm (and potentially 675 mm) can be supported[Reference Lu and Kimbel66], which can serve as the compressor for the TW-class mid-IR OPCPA systems.
Finally, we want to point out that the thermal effect has not been considered in our simulations due to the lack of temperature-dependent Sellmeier equations for LGN crystal. Because of the high transmittance of LGN to all the three interacting pulses, we expect that the thermal effect is not significant in our demonstrated OPCPA with a 16 W average power. With the increase of average power in the future, the thermal effect should be considered definitely[Reference Rothhardt, Demmler, Hädrich, Peschel, Limpert and Tünnermann67]. A precise characterization of thermal parameters for LGN crystal, e.g., temperature-dependent Sellmeier equations, is the precondition to evaluate the influence of thermal effect on the power scalability of the mid-IR OPCPA.
5 Conclusion
In conclusion, we have proposed a design of a 0.13 TW, seven-cycle,
![]() $5.2~\unicode[STIX]{x03BC}\text{m}$
OPCPA system based on the oxide LGN crystal. The LGN crystal has superior optical characteristics in the mid-IR region and can convert both the broad bandwidth of the 800 nm Ti:sapphire laser and the high power of the 1030 nm Yb:YAG thin-disk laser to the mid-IR few-cycle pulses. We have demonstrated the usability of LGN crystals in the stages of intrapulse DFG and OPCPA by numerical simulations. All the optical sources and key optical instruments used in the design are commercially available. Therefore, the design proposed in this paper is highly feasible. This route may be extended to longer wavelengths beyond
$5.2~\unicode[STIX]{x03BC}\text{m}$
OPCPA system based on the oxide LGN crystal. The LGN crystal has superior optical characteristics in the mid-IR region and can convert both the broad bandwidth of the 800 nm Ti:sapphire laser and the high power of the 1030 nm Yb:YAG thin-disk laser to the mid-IR few-cycle pulses. We have demonstrated the usability of LGN crystals in the stages of intrapulse DFG and OPCPA by numerical simulations. All the optical sources and key optical instruments used in the design are commercially available. Therefore, the design proposed in this paper is highly feasible. This route may be extended to longer wavelengths beyond
![]() $10~\unicode[STIX]{x03BC}\text{m}$
by using another newly developed langasite oxide LGSn crystal. The peak power of this system may be enhanced to the terawatt level by either using a Joule-class pump laser or shortening the pulse duration by nonlinear compression methods. In addition to the long wavelength and high peak power, this mid-IR OPCPA system also combines the advantages of a high repetition rate and passive CEP stability and thereby will become a promising drive source for strong-field physics and attosecond science.
$10~\unicode[STIX]{x03BC}\text{m}$
by using another newly developed langasite oxide LGSn crystal. The peak power of this system may be enhanced to the terawatt level by either using a Joule-class pump laser or shortening the pulse duration by nonlinear compression methods. In addition to the long wavelength and high peak power, this mid-IR OPCPA system also combines the advantages of a high repetition rate and passive CEP stability and thereby will become a promising drive source for strong-field physics and attosecond science.
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (Nos. 61705128, 61727820 and 91850203) and Science and Technology Commission of Shanghai Municipality (Nos. 17YF1409100 and 17ZR1414000). The authors thank Haohai Yu and Dazhi Lu from Shandong University for the discussion of langasite crystals.