1 Introduction
Due to Rayleigh–Taylor instability during inertial confinement fusion (ICF) experiment, the imperfection of capsule surface degrades the final symmetry of the implosion and creates mix at the pusher–fuel interface, potentially quench the ignition[Reference Stephens, Hann and Wilson1, Reference Haan, Amendt and Dittrich2]. Obviously, our goal is to fabricate capsules with perfect surface through optimization of the process of fabrication. However the optimization is based on precise measurement of capsules. Therefore, the ability to precisely characterize the capsule surface is extremely important.
In the 1990s, Lawrence Livermore National Laboratory (LLNL) and General Atomics (GA) developed an atomic force microscope (AFM)-based spheremapper, for mapping the outer surface profiles of ICF capsule[Reference Cook, McEachern and Stephens3]. An average fluctuation power spectrum for capsule surface was established as the National Ignition Facility (NIF) standard for acceptance of capsule surface quality[Reference Haan, Salmonson and Clark4]. Power spectrum became a significant parameter for capsule characterization.
With the progress in capsule fabrication techniques and the increasing requirements for capsule precise characterization in ICF experiments, several surface analysis methods have been developed since 1999[Reference Antipa, Baxamusa and Buice5–Reference Li, Zhang and He7]. Some of them are not adequate. Optical inspection and white-light interferometer cannot detect localized defects or surface roughness less than 1/10 wavelength in height. It is also difficult for these methods to detect micron-sized fluctuations if they do not have abrupt edges on a curved surface. Therefore, an AFM-based profilometer is established to measure surface geometry parameters with nanometer resolution, including an overview of capsule surface mode-power spectrum, surface roughness, roundness and sphericity parameters[Reference Zhao, Sun and Yan8–Reference Zhao, Gao and Ma10]. The capsule, supported on a vacuum chuck, is rotated while an AFM records the circumferential surface profile. A high-precision rotary air bearing with low speed and small diameter is developed to rotate the capsule. Several key techniques, including capsule fast aligning to rotation axis, automatic recording of surface traces in one orbit, and 3D capsule orientation, have been developed to improve the functions of profilometer.
2 Profilometer
The AFM is an effective tool for characterizing the topography of ICF capsules, due to its nanometer resolution and tiny acting force. However, the limited scanning range restricts its application for capsule surface profile measurement. A motion system with nanometer precision is indispensable to cooperate with AFM.
The capsule profilometer setup is shown in Figure 1. The capsule is held with a vacuum chuck while rotating in front of the horizontal AFM tip. The vacuum chuck is mounted on a vertically placed rotary air bearing which provides high-precision low-speed rotation. The shaft encoder of the rotary air bearing reports the shaft angle while the AFM records the surface height information of the capsule. Therefore the surface profile versus the circumferential angle is obtained. In order to measure arbitrary circumferential traces of a capsule, an auxiliary rotation stage is set up on the right for precise reorientation of the capsule. The horizontally laid vacuum chuck is used for mounting and removing the capsule from the rotary air bearing. Two sets of XYZ motorized translation stages precisely control the positions of the AFM tip and the auxiliary vacuum chuck, respectively. The whole apparatus is carefully vibration isolated.
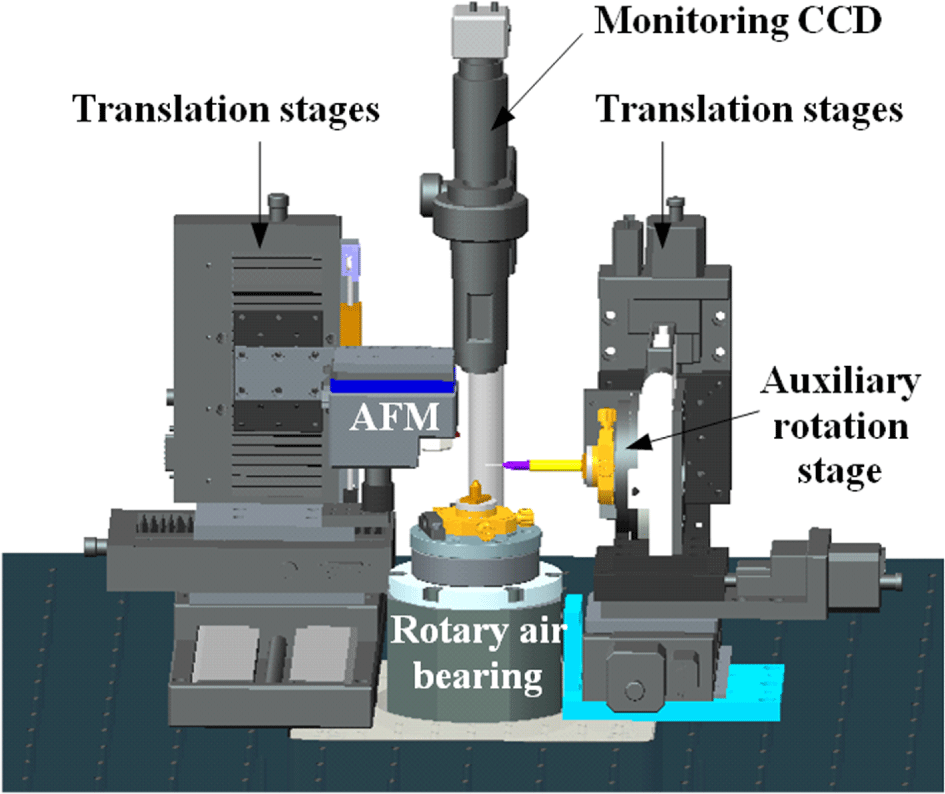
Figure 1. Schematic of capsule profilometer setup.
The small-sized air bearing is composed of aerostatic bearing, torque motor, and circular grating for high precise rotation. The radial rotation error is less than 30 nm. The typical rotational speed is 1–10 rpm. Uniform positioning for more than 36,000 positions of the circumference is realized, with an angular accuracy of less than
![]() $0.005^{\circ }$
.
$0.005^{\circ }$
.
Figure 2 is a photograph of the capsule profilometer. The capsule motion and AFM tip location are monitored by CCD camera during measurement. The CCD video shots are shown in Figure 3.

Figure 2. Photo of capsule profilometer.

Figure 3. CCD video shots during measurement.
2.1 Fast alignment to rotation axis
Before the profile measurement, the capsule center has to be aligned to the rotation axis of the air bearing. In this way, the surface fluctuations of rotated capsule will not exceed the AFM measuring range due to capsule off centeredness. The limited measuring range of AFM and the small diameter of ICF capsule make the aligning process a time-consuming and difficult task, which influences the efficiency of capsule measurement.
To solve this problem, an alignment method of capsule rotation center based on CCD image is proposed, which makes the alignment simple and fast. The aligning process is shown in Figure 4. Firstly, CCD image of the capsule is captured, the capsule edges are picked up and the first position of the capsule center is obtained [Figure 4(a)]. Secondly, the air bearing rotates
![]() $180^{\circ }$
, the first step is repeated and the second position of the capsule center is obtained [Figure 4(b)]. Thirdly, the position of the rotation center is calculated according to the two positions of the capsule center and
$180^{\circ }$
, the first step is repeated and the second position of the capsule center is obtained [Figure 4(b)]. Thirdly, the position of the rotation center is calculated according to the two positions of the capsule center and
![]() $180^{\circ }$
rotation angle. An indicative circle with the rotation center is superimposed onto the CCD video. Finally, the capsule center is aligned to the rotation center until the capsule contour is in coincidence with the indicative circle [Figure 4(c)].
$180^{\circ }$
rotation angle. An indicative circle with the rotation center is superimposed onto the CCD video. Finally, the capsule center is aligned to the rotation center until the capsule contour is in coincidence with the indicative circle [Figure 4(c)].

Figure 4. The process steps of capsule center alignment.
After the aligning step, the eccentricity of the capsule center is restricted to less than
![]() $3~\unicode[STIX]{x03BC}\text{m}$
in rotation. The aligning process takes about 3 min, which greatly improves the profiling efficiency and guarantees a measurement progress of six capsules per day.
$3~\unicode[STIX]{x03BC}\text{m}$
in rotation. The aligning process takes about 3 min, which greatly improves the profiling efficiency and guarantees a measurement progress of six capsules per day.
2.2 Automatic recording of surface traces
In order to improve the profiling efficiency, automatic measurement of surface traces is essential. In 3D reconstruction, we use several orbits to cover the entire capsule, and each orbit contains large amount of parallel traces. Automatic measurement of traces enlarges the covering area in single orbit, thus shortens the time for complete coverage measurement and ensures the reconstruction accuracy.
An algorithm is developed to center the AFM tip on the capsule’s equator before measurement, by operating the motorized
![]() $z$
-displacement and
$z$
-displacement and
![]() $x$
-displacement stages, as shown in Figure 5. In addition, the
$x$
-displacement stages, as shown in Figure 5. In addition, the
![]() $z$
-displacement stage automatically offsets the AFM tip for parallel traces in orbit measurement and the
$z$
-displacement stage automatically offsets the AFM tip for parallel traces in orbit measurement and the
![]() $y$
-displacement stage compensates the shift caused by
$y$
-displacement stage compensates the shift caused by
![]() $z$
-offset so that the tip can be moved along the curve of the capsule.
$z$
-offset so that the tip can be moved along the curve of the capsule.

Figure 5. AFM tip and capsule.

Figure 6. Measured surface traces in one orbit.
With the developed algorithm, the surface traces in one orbit are measured automatically so long as the separation and the number of traces are set. A set of 150 measured traces with
![]() $1~\unicode[STIX]{x03BC}\text{m}$
separation are shown in Figure 6. The diameter of the measured capsule is about
$1~\unicode[STIX]{x03BC}\text{m}$
separation are shown in Figure 6. The diameter of the measured capsule is about
![]() $900~\unicode[STIX]{x03BC}\text{m}$
. Surface fluctuations occur in adjacent traces at the same angle, due to local defects on capsule surface.
$900~\unicode[STIX]{x03BC}\text{m}$
. Surface fluctuations occur in adjacent traces at the same angle, due to local defects on capsule surface.
2.3 Precise capsule reorientation
The standard procedure to acquire surface power spectrum of one capsule is to calculate the fluctuation power from the average of the Fourier transform of nine surface profiles[Reference Cook, McEachern and Stephens3]. The nine profiles are taken along three parallel traces in three mutually orthogonal great circles, which is the standard trace pattern [Figure 7(a)]. Another pattern is the complete coverage pattern [Figure 7(b)], in which case the capsule surface is completely covered by several polar and equatorial orbits[Reference Stephens, Olson and Huang11]. Both patterns require precise control of capsule reorientation between two orbits measurement. Capsule reorientation is realized by two orthogonal shafting, and the auxiliary shaft is strictly perpendicular to the air bearing.

Figure 7. Trace patterns for capsule measurement.
The reorientation accuracy is the key to ensure the complete surface mapping and 3D surface reconstruction. There is always a slight bobble in picking up and replacing the capsule, which influences the reconstruction accuracy. Therefore, the reorientation accuracy needs exact determination.
The suction force of the vacuum chuck is set appropriate to avoid capsule deformation and ensure the flexible operation in capsule repositioning. Based on calculations and experimental results, we designed and built a vacuum chuck with tiny suction force, which is through the shaft center. The capsule deformation caused by vacuum chuck is estimated to be one order of magnitude lower than capsule sphericity error.
The two orthogonal shafting are repeatedly adjusted according to the feature points on capsule surface, which finally guarantees the precise reorientation of the capsule. Two micropores are imposed on capsule surface by femtosecond laser ablation. As shown in Figure 8, with the obtained traces before and after reorientation operation, the reorientation accuracy can be calculated according to the position differences of micropores. As a result, the bobble in manipulating a capsule is less than
![]() $2.5^{\circ }$
in each coordinate direction.
$2.5^{\circ }$
in each coordinate direction.

Figure 8. Traces (a) before and (b) after capsule repositioning of
![]() $360^{\circ }$
.
$360^{\circ }$
.
2.4 Noise power spectrum
Noise power spectra are shown in Figure 9, in which the blue curve and the red curve, respectively, represent our profilometer and NIF spheremapper. The measurement uncertainty of our profilometer is calculated according to the surface roughness value of noise power spectrum, and is 1.7 nm.

Figure 9. Noise power spectra.
3 Surface topography characterization
Based on the developed profilometer and measured surface traces of the capsule, surface geometry parameters including 1D mode-power spectrum, surface roughness, and roundness can be calculated. With the complete mapping data, the entire capsule surface can be reconstructed and 2D power spectrum is plotted. Therefore the characterization of the entire surface is realized and the capsule surface quality can be evaluated.
3.1 Complete surface measurement and 3D reconstruction
Complete surface measurement is based on precise capsule reorientation and automatic recording of surface traces. After the recording of circumference traces in one orbit, the capsule is orientated several times with equal interval angle by the operation of two orthogonal shafting, to cover the entire surface. As shown in Figure 10, a glow discharge polymer (GDP) capsule with 2 mm diameter is covered by four orbits separated by
![]() $45^{\circ }$
. Each orbit is
$45^{\circ }$
. Each orbit is
![]() $800~\unicode[STIX]{x03BC}\text{m}$
wide. The small height difference between the four orbits is mainly caused by the position error at different directions. The yellow protuberant features on the sphere are due to the local defects such as spikes on the capsule surface.
$800~\unicode[STIX]{x03BC}\text{m}$
wide. The small height difference between the four orbits is mainly caused by the position error at different directions. The yellow protuberant features on the sphere are due to the local defects such as spikes on the capsule surface.

Figure 10. Orbits covering the complete surface.
The complete mapping data needs preprocessing before surface reconstruction. Profilometer only measures the deviation from a circle, not the radius itself. As a result, mode 0 (the average radius) and mode 1 (circle center) must be first retrieved for each trace to minimize the radius discrepancy and trace intersections[Reference Huang, Stephens and Gibson12]. Second, a 2D filtering algorithm based on discrete cosine transform is applied to the surface data in one orbit[Reference Garcia13], in order to eliminate abnormal fluctuations of adjacent traces and reduce the errors caused by environmental noise and AFM tip shifting.
After data preprocessing, all orbit data is combined and aligned according to initial measured positions, and the spherical surface map
![]() $R(\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
is obtained. The angular resolution of
$R(\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
is obtained. The angular resolution of
![]() $R(\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
is
$R(\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
is
![]() $1^{\circ }$
with
$1^{\circ }$
with
![]() $360\times 360$
sampling.
$360\times 360$
sampling.
![]() $R(\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
is expressed as a linear combination of spherical harmonic functions[Reference Groemer14],
$R(\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
is expressed as a linear combination of spherical harmonic functions[Reference Groemer14],
where
![]() $A_{l,m}$
represents the spherical harmonic coefficient, and
$A_{l,m}$
represents the spherical harmonic coefficient, and
![]() $Y_{l,m}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
represents the spherical harmonic function.
$Y_{l,m}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
represents the spherical harmonic function.
After the spherical harmonic expansion, the entire capsule surface is reconstructed with different orders, as shown in Figure 11. The construction results with 0–20 orders, 21–250 orders and 251–301 orders, respectively, demonstrate the surface fluctuations with low frequency, intermediate frequency and high frequency. The sphere direction is rotated (compared with Figure 10) for better demonstration.

Figure 11. Surface reconstruction with different orders.
3.2 Surface characterization with mode-power spectrum
The surface traces measured by profilometer reflect the characteristic of capsule surface. Different modes (frequencies) of capsule surface fluctuations have diverse effects on the hydrodynamic instability in implosion. To exactly evaluate the influence, the amplitude of fluctuations at each concerned mode must be acquired. Therefore, the mode-spectrum curve which gives the relationship between surface fluctuation mode and its amplitude becomes a significant parameter to estimate the capsule performance in ICF experiment.
The circumferential trace data by profile measurement is a one-dimensional discrete time sequence. The harmonic component at each mode can be obtained by Fourier transform. The 1D mode-power spectrum is plotted with the mode as horizontal coordinate and the square of the amplitude for each harmonic component as the longitudinal coordinate[Reference Cook, McEachern and Stephens3]. The 1D mode-power spectrum indicates the height fluctuations of surface harmonic components for different frequency distribution.
The measured profile traces of capsule surface and the calculated mode-power spectrum curves are shown in Figure 12. The RMS surface roughness for different mode regions can be directly calculated from the mode-power spectrum.

Figure 12. (a) Surface profile traces and (b) corresponding 1D mode-power spectrum.
Compared with 1D power spectrum, 2D power spectrum is more effective for characterization of the entire capsule surface. Based on the spherical harmonic analysis of complete mapping data, the 2D power spectrum is calculated for entire surface evaluation.
For a 2 mm diameter GDP capsule, the spherical surface map
![]() $R(\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
is obtained after several orbits measurement (Figure 10). According to the theory of spherical harmonic transform, the 2D power spectrum with spherical harmonic order is calculated by,
$R(\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
is obtained after several orbits measurement (Figure 10). According to the theory of spherical harmonic transform, the 2D power spectrum with spherical harmonic order is calculated by,
As shown in Figure 13, the 2D spherical harmonic power spectrum quantitatively reflects the frequency distribution information for capsule entire surface topography. Rapid growing of surface fluctuations for low order leads to deformation in implosion compression, and high order components will induce mixture at interface due to hydrodynamic instabilities.

Figure 13. 2D power spectrum curve.
3.3 Application
The successful establishment of capsule surface profilometer greatly promotes the fabrication of ICF capsules. On the other hand, the precise characterization of capsule surface ensures capsule quality for ICF experiments, and provides complete capsule morphology parameters for numerical simulation research. As shown in Figure 14, the amplitudes of power spectrum curves with different surface quality have difference of three orders of magnitude.

Figure 14. Power spectrum curves with (a) good surface quality and (b) bad surface quality.
The initial morphology of the capsule is the vital factor that affecting the implosion performance. The capsule power spectra obtained by profilometer provide significant import data for quantitative interpretation of various non-one-dimensional factors on implosion performance, and comparison between the experimental results and numerical simulations.
4 Conclusion
Based on AFM and high-precision rotary air bearing, a capsule profilometer is developed with nanometer resolution for surface profile measurement of ICF capsule. To evaluate the capsule quality, 1D and 2D power spectra are calculated with the measured surface traces with measurement uncertainty of 1.7 nm and capsule reorientation error of less than
![]() $2.5^{\circ }$
. With the developed techniques including capsule fast aligning to rotation axis and automatic recording of orbit traces, the measuring efficiency of six capsules per day is realized.
$2.5^{\circ }$
. With the developed techniques including capsule fast aligning to rotation axis and automatic recording of orbit traces, the measuring efficiency of six capsules per day is realized.


















