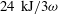1. Introduction
Fast ignition (FI)[Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1–Reference Honrubia and Meyer-ter-Vehn3]is an ignition scheme for inertial confinement fusion (ICF). In this two-step ICF scheme, the fuel pellet is first compressed to a high density
![]() ${\sim } 300~ {\rm g}~ {\rm cm}^{-3}$
, and then this highly compressed deuterium–tritium pellet (
${\sim } 300~ {\rm g}~ {\rm cm}^{-3}$
, and then this highly compressed deuterium–tritium pellet (
![]() $10\mbox{--}20~ \mu {\rm m}$
at its core) is ignited by a
$10\mbox{--}20~ \mu {\rm m}$
at its core) is ignited by a
![]() ${\sim }10~ {\rm ps}$
, 10 kJ intense flux of MeV electrons (or ions). These high-energy particles are generated by the absorption of an ultra-intense petawatt laser, at the edge of the pellet, which is usually
${\sim }10~ {\rm ps}$
, 10 kJ intense flux of MeV electrons (or ions). These high-energy particles are generated by the absorption of an ultra-intense petawatt laser, at the edge of the pellet, which is usually
![]() ${\sim }50~ \mu {\rm m}$
away from the dense core. Previous studies[Reference Key, Adam, Akli, Borghesi, Chen, Evans, Freeman, Habara, Hatchett, Hill, Heron, King, Kodama, Lancaster, Mackinnon, Patel, Phillips, Romagnani, Snavely, Stephens, Stoeckl, Town, Toyama, Zhang, Zepf and Norreys4]showed that electrons with 1–3 MeV energy are optimal for FI. In order to accelerate electrons to these energies, the ultra-intense petawatt laser needs an intensity of
${\sim }50~ \mu {\rm m}$
away from the dense core. Previous studies[Reference Key, Adam, Akli, Borghesi, Chen, Evans, Freeman, Habara, Hatchett, Hill, Heron, King, Kodama, Lancaster, Mackinnon, Patel, Phillips, Romagnani, Snavely, Stephens, Stoeckl, Town, Toyama, Zhang, Zepf and Norreys4]showed that electrons with 1–3 MeV energy are optimal for FI. In order to accelerate electrons to these energies, the ultra-intense petawatt laser needs an intensity of
![]() ${>}10^{19}~ {\rm W}~ {\rm cm}^{-2}$
, a pulse duration of
${>}10^{19}~ {\rm W}~ {\rm cm}^{-2}$
, a pulse duration of
![]() ${<}20~ {\rm ps}$
, a spot size of
${<}20~ {\rm ps}$
, a spot size of
![]() ${<}20~ \mu {\rm m}$
, and a laser contrast of
${<}20~ \mu {\rm m}$
, and a laser contrast of
![]() ${>}10^8$
. This two-step process, which separates fuel assembly and ignition, could relax the driver requirements and promise high gains[Reference Atzeni, Schiavi, Honrubia, Ribeyre, Schurtz, Nicolai, Olazabal-Loume, Bellei, Evans and Davies2].
${>}10^8$
. This two-step process, which separates fuel assembly and ignition, could relax the driver requirements and promise high gains[Reference Atzeni, Schiavi, Honrubia, Ribeyre, Schurtz, Nicolai, Olazabal-Loume, Bellei, Evans and Davies2].
Investigations of the FI scheme are challenging and involve extremely high-energy-density physics, including, for example, ultra-intense lasers with intensities larger than
![]() $10^{19}~ {\rm W}~ {\rm cm}^{-2}$
, pressures in excess of 1 Gbar, magnetic fields in excess of 100 MG, and electric fields in excess of
$10^{19}~ {\rm W}~ {\rm cm}^{-2}$
, pressures in excess of 1 Gbar, magnetic fields in excess of 100 MG, and electric fields in excess of
![]() $10^{12}~ {\rm V}~ {\rm m}^{-1}$
. Addressing this complexity and the scale of the physical issue inherently requires high-energy and high-power laser facilities that are now becoming available, as well as the most advanced theory and computer simulation capability available[5]. Nowadays, a number of laser facilities are currently performing experiments for FI, including, for example, the OMEGA facility at the laboratory for laser energetic (LLE) at the University of Rochester, the FIREX-I at the Institute of Laser Engineering (ILE) in Osaka University, the Shenguang-II upgraded laser facility in Shanghai, the Trident laser facility at the Los Alamos National Laboratory, the Petal facility in France, and the Vulcan facility at the Rutherford Appleton Laboratory in the UK. New facilities are in different stages of design or construction, such as the NIF-ARC at the Lawrence Livermore National Laboratory (LLNL) and the FI Realization Experiment in Japan. Many experiments have been carried out to study the generation of high-energy particles using ultra-intense laser pulses and the feasibility of FI with these high-energy particles[Reference Kodama, Shiraga, Shigemori, Toyama, Fujioka, Azechi, Fujita, Habara, Hall, Izawa, Jitsuno, Kitagawa, Krushelnick, Lancaster, Mima, Nagai, Nakai, Nishimura, Norimatsu, Norreys, Sakabe, Tanaka, Youssef, Zepf and Yamanaka6–Reference Ma, Sawada, Patel, Chen, Divol, Higginson, Kemp, Key, Larson, Le Pape, Link, MacPhee, McLean, Ping, Stephens, Wilks and Beg8].
$10^{12}~ {\rm V}~ {\rm m}^{-1}$
. Addressing this complexity and the scale of the physical issue inherently requires high-energy and high-power laser facilities that are now becoming available, as well as the most advanced theory and computer simulation capability available[5]. Nowadays, a number of laser facilities are currently performing experiments for FI, including, for example, the OMEGA facility at the laboratory for laser energetic (LLE) at the University of Rochester, the FIREX-I at the Institute of Laser Engineering (ILE) in Osaka University, the Shenguang-II upgraded laser facility in Shanghai, the Trident laser facility at the Los Alamos National Laboratory, the Petal facility in France, and the Vulcan facility at the Rutherford Appleton Laboratory in the UK. New facilities are in different stages of design or construction, such as the NIF-ARC at the Lawrence Livermore National Laboratory (LLNL) and the FI Realization Experiment in Japan. Many experiments have been carried out to study the generation of high-energy particles using ultra-intense laser pulses and the feasibility of FI with these high-energy particles[Reference Kodama, Shiraga, Shigemori, Toyama, Fujioka, Azechi, Fujita, Habara, Hall, Izawa, Jitsuno, Kitagawa, Krushelnick, Lancaster, Mima, Nagai, Nakai, Nishimura, Norimatsu, Norreys, Sakabe, Tanaka, Youssef, Zepf and Yamanaka6–Reference Ma, Sawada, Patel, Chen, Divol, Higginson, Kemp, Key, Larson, Le Pape, Link, MacPhee, McLean, Ping, Stephens, Wilks and Beg8].
Research has shown that most potential sources of offset in fuel compression are also potential problems in standard conventional hot-spot shells and are well enough controlled that they are not a problem[Reference Stephens, Hatchett, Tabak, Stoeckl, Shiraga, Fujioka, Bonino, Nikroo, Petrasso, Sangster, Smith and Tanaka9]. Now most FI research works is focused on the generation, transport, and deposition of high-energy particles[Reference Lancaster, Green, Hey, Akli, Davies, Clarke, Freeman, Habara, Key, Kodama, Krushelnick, Murphy, Nakatsutsumi, Simpson, Stephens, Stoeckl, Yabuuchi, Zepf and Norreys10–Reference Strozzi, Tabak, Larson, Divol, Kemp, Bellei, Marinak and Key19]. There are usually three important stages in the interaction of an ultra-intense petawatt laser pulse with a solid target. In the first stage, the solid target is heated by the laser prepulse, resulting in the formation of the preplasma. Usually, the scale of this preplasma can be very large (
![]() ${\sim } 100~ \mu {\rm m}$
) depending on the prepulse level. After the formation of the preplasma, the subsequent main laser pulse propagates inside the underdense plasma, and the nonlinear interaction of the laser pulse and the relativistic plasma plays an important role in the laser propagation and relativistic electron beam (REB) generation. In this stage, the crucial point is how to produce a sufficient number of well-collimated relativistic electrons with an appropriate energy range. In the second stage, the relativistic electrons escape from the laser fields when they enter into the overdense plasma. The relativistic electrons transport from the critical density to the core densities (
${\sim } 100~ \mu {\rm m}$
) depending on the prepulse level. After the formation of the preplasma, the subsequent main laser pulse propagates inside the underdense plasma, and the nonlinear interaction of the laser pulse and the relativistic plasma plays an important role in the laser propagation and relativistic electron beam (REB) generation. In this stage, the crucial point is how to produce a sufficient number of well-collimated relativistic electrons with an appropriate energy range. In the second stage, the relativistic electrons escape from the laser fields when they enter into the overdense plasma. The relativistic electrons transport from the critical density to the core densities (
![]() $n_e \sim 10^{26}~ {\rm cm}^{-3}$
). During the transport, the electrons lose their energy before reaching the core due to the collisional effect and collective stopping. The crucial point in this stage is how to control the beam filamentation and collimate the REBs. In the third stage, the REBs reach the compressed fuel and deposit their energy in a small volume by collisions, and finally ignite the fuel.
$n_e \sim 10^{26}~ {\rm cm}^{-3}$
). During the transport, the electrons lose their energy before reaching the core due to the collisional effect and collective stopping. The crucial point in this stage is how to control the beam filamentation and collimate the REBs. In the third stage, the REBs reach the compressed fuel and deposit their energy in a small volume by collisions, and finally ignite the fuel.
We have been developing our integrated simulation codes to investigate FI sciences. The integrated codes include a radiation hydrodynamic code, a particle-in-cell (PIC) simulation code, and a hybrid PIC code. With the help of these codes, we designed an advanced cone–wire-in-shell target for FI, and undertook the systematic research for the generation, transport, and deposition of the fast electrons.
2. Integrated fast ignition simulation codes
While the basic idea for FI is straightforward, the realization of this technique, particularly for the injection of the petawatt ultra-intense laser beam, relies upon a systematic understanding of many complex physical issues, ranging from nonlinear laser-plasma interactions to REB transport through dense plasmas[Reference Van Woerkom, Akli, Bartal, Beg, Chawla, Chen, Chowdhury, Freeman, Hey, Key, King, Link, Ma, Mackinnon, MacPhee, Offermann, Ovchinnikov, Patel, Schumacher, Stephens and Tsui20]. In order to deal adequately with the complexities of the FI physics, simulations should play an important role in understanding the physics and exciting new ideas for FI. However, the physical processes in FI are very complex. Since they have different time scales, large spatial ranges and multi-physics, it is impossible to simulate all the FI processes within one code. Recently, we have developed an ‘Integrated Code for Fast Ignition’ at the IAPCM (ICFI), which consists of a 2D3V/3D3V (two/three dimensions in space and three dimensions in velocity) relativistic collisional PIC code ASCENT, two-dimensional radiation hydrodynamic codes LARED-S[Reference Pei21]and XB2D, hybrid fluid–PIC codes EBT2D&3D[Reference Cao, Chang, Pei, Liu, Li and Zheng22, Reference Cao, Pei, Liu, Chang, Li and Zheng23]and HFPIC[Reference Zhou, He and Yu24].
The typical scenario in the ICFI is summarized as follows. LARED-S, which is multi-dimensional, massively parallel and Eulerian-mesh-based radiation-hydrodynamic code, computes the implosion dynamics of a cone-in-shell FI target. ASCENT, which obtains the density profile at the maximum compression time from LARED-S, simulates the interaction of an ultra-intense petawatt laser pulse with this obtained-profile plasma target. The transport modeling is done with the hybrid fluid–PIC codes EBT2D&3D and HFPIC. The hybrid codes receive the distribution functions of the REBs produced by the ultra-intense laser pulse from ASCENT, and then models the PIC-simulated electron transport through a collisional plasma. Finally, the fuel heating and thermonuclear burn are simulated again with the radiation-hydrodynamic code LARED-S. A schematic diagram of the ICFI is presented in Figure 1. Besides the ICFI codes, we also developed a relativistic Fokker–Planck code which helps to model the energy deposition together with the hybrid–PIC codes. In the following sections, we will introduce these codes and the physical research.

Figure 1. (Color online) A schematic diagram of the ICFI at the IAPCM.
3. 2D radiation hydrodynamics simulation
The implosion dynamics of a cone-in-shell FI target is simulated by LARED-S[Reference Pei21], which is a two-dimensional radiation hydrodynamics code including laser ray tracing, multi-group radiation diffusion, electron and ion thermal conduction, atomic physics, nuclear reaction, alpha particle transport, and the quotidian equations of state.
In order to increase the fast electron transport efficiency, a variant target design containing a reentrant cone coupled wire is introduced to guide the fast electrons. The wire attached to the tip of the gold cone is surrounded by low-
![]() $Z$
materials, providing a high-resistivity-core–low-cladding target structure. Megagauss (MG) magnetic fields can be produced around the wire, which can collimate fast electrons and enhance the transport efficiency. But during the implosion, the nonthermal Au M-band lines in the emissions from the Au hohlraum are absorbed by the high-
$Z$
materials, providing a high-resistivity-core–low-cladding target structure. Megagauss (MG) magnetic fields can be produced around the wire, which can collimate fast electrons and enhance the transport efficiency. But during the implosion, the nonthermal Au M-band lines in the emissions from the Au hohlraum are absorbed by the high-
![]() $Z$
cone and wire. A dense vapor layer is generated on their surface, which is Raleigh–Taylor unstable against the pressures exerted by the lower-density gas escaping the collapsing shell and mixes with it[Reference Stephens, Hatchett, Tabak, Stoeckl, Shiraga, Fujioka, Bonino, Nikroo, Petrasso, Sangster, Smith and Tanaka9]. In order to avoid the expansion of the Au cone, we use a plastic (CH) coating on the gold cone and wire surfaces. The implosions of the cone–wire-in-shell with and without the CH coating are investigated by LARED-S. As shown in Figure 2, the cone–wire structure survives at the maximal compression time. However, the high-
$Z$
cone and wire. A dense vapor layer is generated on their surface, which is Raleigh–Taylor unstable against the pressures exerted by the lower-density gas escaping the collapsing shell and mixes with it[Reference Stephens, Hatchett, Tabak, Stoeckl, Shiraga, Fujioka, Bonino, Nikroo, Petrasso, Sangster, Smith and Tanaka9]. In order to avoid the expansion of the Au cone, we use a plastic (CH) coating on the gold cone and wire surfaces. The implosions of the cone–wire-in-shell with and without the CH coating are investigated by LARED-S. As shown in Figure 2, the cone–wire structure survives at the maximal compression time. However, the high-
![]() $Z$
material is mixed and diffused into the core of the compressed core in the case without the CH coating. In contrast, in the case with the CH coating, the interface of the high-
$Z$
material is mixed and diffused into the core of the compressed core in the case without the CH coating. In contrast, in the case with the CH coating, the interface of the high-
![]() $Z$
and low-
$Z$
and low-
![]() $Z$
material is very clear and the high-
$Z$
material is very clear and the high-
![]() $Z$
material does not enter into the compressed core. This means the CH coating works well in preventing the expansion of the high-
$Z$
material does not enter into the compressed core. This means the CH coating works well in preventing the expansion of the high-
![]() $Z$
plasma.
$Z$
plasma.

Figure 2. (Color online) Mass density contours of the cone–wire-in-shell target in LASER-S simulations. (a) and (b) are without the CH coating, (c) and (d) are with the CH coating. Black lines represent the contact surfaces between gold and the low-
![]() $Z$
materials.
$Z$
materials.
Another issue is that an ultraintense laser pulse is usually accompanied with a long prepulse of ASE (amplified spontaneous emission). The ASE pulses have a typical pulse of 0.5–8 ns and a contrast of
![]() $10^{-9}\mbox{--}10^{-6}$
. This ASE pulse usually creates a plasma corona. Here, the initial PIC simulation parameters of the preplasma of the gold cone target after the irradiation of the ASE pulse is also studied with the radiation hydrodynamic code. We will discuss it in the following section.
$10^{-9}\mbox{--}10^{-6}$
. This ASE pulse usually creates a plasma corona. Here, the initial PIC simulation parameters of the preplasma of the gold cone target after the irradiation of the ASE pulse is also studied with the radiation hydrodynamic code. We will discuss it in the following section.
4. Laser–plasma interaction (LPI) modeling with the PIC code
Our LPI simulations are performed with the relativistic PIC code ASCENT. In many settings in plasma physics, a first-principle PIC simulation is still the most suitable tool for understanding the physics. However, by their nature, large-scale explicit PIC simulations require huge computing resources. Here, our code has recently been reconstructed on an infrastructure named JASMIN, which is aimed at structured or adaptive block-structured meshes for numerical simulations of complex systems on parallel computers[Reference Mo, Zhang, Cao, Liu, Xu, An, Pei and Zhu25]. Using JASMIN, our code can efficiently use thousands and tens of thousands of CPU processors.
In the previous section, we have shown that the cone–wire structure survives at the maximal compression time during the implosion. The collimation effect of quasistatic magnetic fields on the transport of REBs in these specially engineered structure targets was investigated by our PIC simulations[Reference Cai, Zhu, Chen, Wu, He and Mima26–Reference Wu, Zhou and Zhu29]. The PIC simulations showed that in the high-resistivity-core–low-resistivity-cladding structure targets, the magnetic fields on the interfaces are generated by the gradients of the resistivity and the REB current, while in the low-density-core–high-density-cladding structure targets, the magnetic fields are generated by the nonparallel density gradients and the fast-electron current near the interface[Reference Cai, Zhu, He, Wu, Chen, Zhou, Yu and Nagatomo27]. The generated quasistatic magnetic fields are as high as several or several tens of MG, which are strong enough to collimate fast electrons.
Such a strong imposed magnetic field has also been demonstrated with a capacitor–coil target and an ns–kJ laser without compression[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahare, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi30]. It seems that the imposed magnetic field raises great hopes by controlling the electron divergence and lowering the laser energy required to obtain the fuel burning for FI. In our work[Reference Cai, Zhu and He31], the interaction of an ultraintense laser pulse with overdense plasma with different imposed magnetic fields is investigated by ASCENT. It has been shown that, in the case without imposed magnetic field, the fast electrons, only carrying about 7% of the total input laser energy, can transport 42 microns from the interaction region to the boundary. In comparison, in the case with
![]() $B_0>3~ {\rm MG}$
, the fast electrons, carrying about 20% of the total input laser energy, can transport to the boundary. However, it was also found that the divergence angle increases with increase of the laser intensity. Therefore, an imposed magnetic field with
$B_0>3~ {\rm MG}$
, the fast electrons, carrying about 20% of the total input laser energy, can transport to the boundary. However, it was also found that the divergence angle increases with increase of the laser intensity. Therefore, an imposed magnetic field with
![]() $B_0= 3\mbox{--}30~ {\rm MG}$
may be a suitable value for collimating the fast electrons. Furthermore, we also studied the effects of the background plasma temperature on the current filamentation instability and the growth of the fine-structure magnetic fields. We found a new way to suppress the current filamentation instability and its detrimental effects on the fast-electron beam divergence.
$B_0= 3\mbox{--}30~ {\rm MG}$
may be a suitable value for collimating the fast electrons. Furthermore, we also studied the effects of the background plasma temperature on the current filamentation instability and the growth of the fine-structure magnetic fields. We found a new way to suppress the current filamentation instability and its detrimental effects on the fast-electron beam divergence.
Studies have shown that the nanosecond ASE prepulse usually produces a large-scale preplasma with size
![]() $30\mbox{--}100~ \mu {\rm m}$
. The large-scale preplasma plays an important role in the generation of the fast electrons. Studies[Reference Key, Adam, Akli, Borghesi, Chen, Evans, Freeman, Habara, Hatchett, Hill, Heron, King, Kodama, Lancaster, Mackinnon, Patel, Phillips, Romagnani, Snavely, Stephens, Stoeckl, Town, Toyama, Zhang, Zepf and Norreys4]have also shown that fast electrons with energy 1–3 MeV are optimal for heating the dense core. Our simulations[Reference Wang, Cai, Jia and Zhu32, Reference Cai, Mima, Sunahara, Johzaki, Nagatomo, Zhu and He35]show that, in the large-scale preplasma, stochastic heating can accelerate electrons to very high energies, carrying a significant fraction of input laser energy and decreasing the laser coupling efficiency to the compressed core. However, few simulations have been performed on how the preplasma inside the cone can affect the generation of the fast electrons for FI. MacPhee[Reference MacPhee, Divol, Kemp, Akli, Beg, Chen, Chen, Hey, Fedosejevs, Freeman, Henesian, Key, Le Pape, Link, Ma, Mackinnon, Ovchinnikov, Patel, Phillips, Stephens, Tabak, Town, Tsui, Van Woerkom, Wei and Wilks36]and Akli[Reference Akli, Orban, Schumacher, Storm, Fatenejad, Lamb and Freeman37]have simulated a cone with preplasma inside, and have shown that the preplasma significantly reduces the forward-going component of 2–4 MeV electrons. Both of the simulation parameters are fitted to the Titan laser facility, which delivers
$30\mbox{--}100~ \mu {\rm m}$
. The large-scale preplasma plays an important role in the generation of the fast electrons. Studies[Reference Key, Adam, Akli, Borghesi, Chen, Evans, Freeman, Habara, Hatchett, Hill, Heron, King, Kodama, Lancaster, Mackinnon, Patel, Phillips, Romagnani, Snavely, Stephens, Stoeckl, Town, Toyama, Zhang, Zepf and Norreys4]have also shown that fast electrons with energy 1–3 MeV are optimal for heating the dense core. Our simulations[Reference Wang, Cai, Jia and Zhu32, Reference Cai, Mima, Sunahara, Johzaki, Nagatomo, Zhu and He35]show that, in the large-scale preplasma, stochastic heating can accelerate electrons to very high energies, carrying a significant fraction of input laser energy and decreasing the laser coupling efficiency to the compressed core. However, few simulations have been performed on how the preplasma inside the cone can affect the generation of the fast electrons for FI. MacPhee[Reference MacPhee, Divol, Kemp, Akli, Beg, Chen, Chen, Hey, Fedosejevs, Freeman, Henesian, Key, Le Pape, Link, Ma, Mackinnon, Ovchinnikov, Patel, Phillips, Stephens, Tabak, Town, Tsui, Van Woerkom, Wei and Wilks36]and Akli[Reference Akli, Orban, Schumacher, Storm, Fatenejad, Lamb and Freeman37]have simulated a cone with preplasma inside, and have shown that the preplasma significantly reduces the forward-going component of 2–4 MeV electrons. Both of the simulation parameters are fitted to the Titan laser facility, which delivers
![]() $(150 \pm 10)~ {\rm J}$
in
$(150 \pm 10)~ {\rm J}$
in
![]() $0.7 \pm 0.2~ {\rm ps}$
. However, in the FI scheme, the heating laser beam has to deliver
$0.7 \pm 0.2~ {\rm ps}$
. However, in the FI scheme, the heating laser beam has to deliver
![]() ${>}200~ {\rm kJ}$
in 20 ps. On the other hand, we find that a specially designed target, such as a double cone, can reduce the detrimental effect of the prepulse (as shown as in Figure 3). Therefore, how the prepulse of the heating laser beam affects the forward-going fast electrons in the FI scenario still needs further research[Reference Cai, Zhu and He31].
${>}200~ {\rm kJ}$
in 20 ps. On the other hand, we find that a specially designed target, such as a double cone, can reduce the detrimental effect of the prepulse (as shown as in Figure 3). Therefore, how the prepulse of the heating laser beam affects the forward-going fast electrons in the FI scenario still needs further research[Reference Cai, Zhu and He31].

Figure 3. (Color online) Initial density profile of the double-cone target (a) without and (b) with large-scale preplasma.

Figure 4. (Color online) The natural logarithm of the electron energy density for (a), (b) without and (c), (d) with large-scale preplasma at time (a), (c)
![]() $t = 500~ {\rm fs}$
, and (b), (d)
$t = 500~ {\rm fs}$
, and (b), (d)
![]() $t = 1000~ {\rm fs}$
.
$t = 1000~ {\rm fs}$
.
In our simulations, this physics is modeled in two parts: (a) the radiation-hydrodynamic code XB2D is used to calculate the distribution of the preformed plasma created by the laser prepulse inside the inner cone, and the obtained electron and ion density profiles are exported to the PIC code ASCENT; (b) ASCENT is used to study the interaction of an ultra-intense ultra-short laser pulse with the preformed plasma from the XB2D code with a high fidelity. Figure 3(a) is a sketch of the geometry of the simulations. In our double-cone target the inner cone wall is isolated from the background plasma (corona plasma) by a vacuum gap. The width of the inner cone wing is
![]() $5\lambda _0$
and the width of the gap is
$5\lambda _0$
and the width of the gap is
![]() $3\lambda _0$
. Here,
$3\lambda _0$
. Here,
![]() $\lambda _0$
is the wavelength of the incident laser pulse. The plasma consists of three species: electrons, protons with
$\lambda _0$
is the wavelength of the incident laser pulse. The plasma consists of three species: electrons, protons with
![]() $m_p/m_e = 1836$
outside the cone, and heavy ions (the Au ion with an assumed charge state
$m_p/m_e = 1836$
outside the cone, and heavy ions (the Au ion with an assumed charge state
![]() $Z_i = 40$
). Both the plasma density of the gold cone and that of the hydrogen plasma are
$Z_i = 40$
). Both the plasma density of the gold cone and that of the hydrogen plasma are
![]() $40 n_c$
. The p-polarized laser pulse at a wavelength of
$40 n_c$
. The p-polarized laser pulse at a wavelength of
![]() $\lambda _0 = 1.06~ \mu {\rm m}$
and with a intensity of
$\lambda _0 = 1.06~ \mu {\rm m}$
and with a intensity of
![]() $1.2\times 10^{19}~ {\rm W}~ {\rm cm}^{-2}$
irradiates the target from the left boundary.
$1.2\times 10^{19}~ {\rm W}~ {\rm cm}^{-2}$
irradiates the target from the left boundary.
In Figure 4, the energy density distributions of electrons with energies between
![]() $0.5\leq E[MeV]\leq 2$
are plotted. It is clearly seen that the fast electrons are produced at different positions. In the small-scale preplasma case, the fast electrons are mainly produced at the cone tip, as shown in Figure 4(a). Alternatively, in the large-scale preplasma case, the fast electrons are mainly generated at the critical surface which is tens of microns away from the cone tip, as shown in Figure 4(c). In the large-scale preplasma case, the fast electrons that propagate inside the preplasma and cone target experience instabilities and collisions, resulting in energy loss and decreasing the coupling efficiency. Furthermore, since the fast electrons are divergent, more electrons will escape from the side wall in the large-scale preplasma case. We can use a double-cone target to avoid this loss[Reference Cai, Mima, Zhou, Jozaki, Nagatomo, Sunahara and Mason38]. As a consequence, most of the fast electrons are still collimated and transport forward to the cone tip, as shown in Figure 4(d). We also check the forward fast-electron flux, and find that, with the help of the double-cone target, the forward electron flux in the large-scale preplasma case only decreases 2% in comparison with the small-scale preplasma case. This is not so serious compared with the simulations in Refs. [Reference MacPhee, Divol, Kemp, Akli, Beg, Chen, Chen, Hey, Fedosejevs, Freeman, Henesian, Key, Le Pape, Link, Ma, Mackinnon, Ovchinnikov, Patel, Phillips, Stephens, Tabak, Town, Tsui, Van Woerkom, Wei and Wilks36] and [Reference Akli, Orban, Schumacher, Storm, Fatenejad, Lamb and Freeman37].
$0.5\leq E[MeV]\leq 2$
are plotted. It is clearly seen that the fast electrons are produced at different positions. In the small-scale preplasma case, the fast electrons are mainly produced at the cone tip, as shown in Figure 4(a). Alternatively, in the large-scale preplasma case, the fast electrons are mainly generated at the critical surface which is tens of microns away from the cone tip, as shown in Figure 4(c). In the large-scale preplasma case, the fast electrons that propagate inside the preplasma and cone target experience instabilities and collisions, resulting in energy loss and decreasing the coupling efficiency. Furthermore, since the fast electrons are divergent, more electrons will escape from the side wall in the large-scale preplasma case. We can use a double-cone target to avoid this loss[Reference Cai, Mima, Zhou, Jozaki, Nagatomo, Sunahara and Mason38]. As a consequence, most of the fast electrons are still collimated and transport forward to the cone tip, as shown in Figure 4(d). We also check the forward fast-electron flux, and find that, with the help of the double-cone target, the forward electron flux in the large-scale preplasma case only decreases 2% in comparison with the small-scale preplasma case. This is not so serious compared with the simulations in Refs. [Reference MacPhee, Divol, Kemp, Akli, Beg, Chen, Chen, Hey, Fedosejevs, Freeman, Henesian, Key, Le Pape, Link, Ma, Mackinnon, Ovchinnikov, Patel, Phillips, Stephens, Tabak, Town, Tsui, Van Woerkom, Wei and Wilks36] and [Reference Akli, Orban, Schumacher, Storm, Fatenejad, Lamb and Freeman37].
5. Electron transport modeling with the hybrid PIC code
The generation and transport of fast electrons, which are important issues in FI, have been studied with various simulation methods[Reference Welch, Rose, Clark, Genoni and Hughes39, Reference Davies40]. The simulations are usually broken up into two steps because of the disparate spatial and temporal scales involved in the LPI and fast-electron transport. The LPI and generation of fast electrons are simulated with our PIC code ASCENT, while the electron transport is modeled with a hybrid PIC method which permits more coarse temporal and spatial resolutions. The study of fast-electron transport in overdense matter is essential to the success of FI. Here, we developed two different hybrid PIC codes: HFPIC[Reference Zhou, He and Chew41]and EBT2D&3D[Reference Cao, Chang, Pei, Liu, Li and Zheng22, Reference Cao, Pei, Liu, Chang, Li and Zheng23].
The numerical algorithms of the hybrid code HFPIC are similar to those developed by Welch et al. [Reference Welch, Rose, Clark, Genoni and Hughes39], in which both PIC kinetic and fluid electrons are included. The scheme uses a direct implicit particle push and an implicit electromagnetic solver, which relaxes the usual PIC restrictions on the temporal and spatial resolutions and still maintains a good energy conservation. Moreover, the Spitzer resistivity and small-angle scattering are both included, thus allowing us to investigate energetic electron transport in very-high-density plasmas. Such hybrid simulation algorithms have been very successful in modeling the REB transport in a solid or highly compressed high-temperature plasma target[Reference Zhou, He and Chew41–Reference Zhou, Cai, Zhang and He45].
In order to study the field generation and fast-electron collimation at the material interface, a solid target consisting of two materials (Cu inside and Al outside) is considered. For the injected beam with currents greater than the Alfven limit, a return current moves in the opposite direction to establish approximately current-neutral equilibrium, as shown in Figure 5(a). A huge magnetic field of the order of tens of MG is produced as the current filamentation instability develops. The magnetic field at the interface, which is mainly due to the resistivity gradient, can collimate the fast electrons, as shown in Figure 5(b) and 5(d). The plasma is heated due to the Ohmic heating because of the return current (see Figure 5(c)), and the resistivity as well as the space-charge field is thus reduced, allowing the fast electrons to propagate further into the overdense plasmas. In order to enhance the material effects on the transport of the fast electrons, different materials (Au, Cu, Al, and C) are considered. It is found that the use of a low-
![]() $Z$
target material is more efficient for collimating beam electrons as well as generating higher-energy ions[Reference Zhou, Cai, Zhang and He45].
$Z$
target material is more efficient for collimating beam electrons as well as generating higher-energy ions[Reference Zhou, Cai, Zhang and He45].

Figure 5. (Color online) Snapshots of (a) the longitudinal current density Jz(z, r) (in
![]() ${\rm A~ cm}^{-2}$
), (b) the azimuthal magnetic
${\rm A~ cm}^{-2}$
), (b) the azimuthal magnetic
![]() $B_{\theta }$
(in MG), (c) the temperature
$B_{\theta }$
(in MG), (c) the temperature
![]() $T_e$
(in eV) of the target plasma electrons, and (d) the beam density nb (in
$T_e$
(in eV) of the target plasma electrons, and (d) the beam density nb (in
![]() ${\rm cm}^{-3}$
) (from Zhou et al. 2008[Reference Zhou and He42]).
${\rm cm}^{-3}$
) (from Zhou et al. 2008[Reference Zhou and He42]).
The numerical algorithms of the hybrid code EBT2D&3D is different[Reference Cao, Chang, Pei, Liu, Li and Zheng22, Reference Cao, Pei, Liu, Chang, Li and Zheng23]. The background target is treated as a cold and stationary fluid, while the fast electrons are described by the Fokker–Planck equation and solved by the PIC method[Reference Davies40]. Collisions between fast electrons are ignored and the background particles give only drag and random angular scattering terms. The electric field is calculated by Ohms law and the magnetic field is calculated from Faraday’s law. Thus, the effects of the self-generated electric and magnetic fields are considered. Recently, the BPS model for the Coulomb logarithm including the quantum and coupling effects for a wide range of plasma conditions has been supplemented in the code[Reference Brown, Preston and Singleton46–Reference Cao, Chen, He, Yu and Yu48]. These algorithms are much simpler and enable us to do larger-scale simulations. The detailed physics will be published in the near future.
6. Energy deposition modeling with the relativistic Fokker–Planck code
Besides the ICFI codes, we developed a relativistic Fokker–Planck code to model the collisions between fast electrons and core plasma particles[Reference Wu, Zhou, Zhu, Zhang and He49, Reference Wu, Zhang, Zhou, Zhu and He50]. Energy deposition of fast electrons into the core DT plasmas is one of the crucial processes in the FI scenario which will directly influence the overall coupling efficiency and the thermal property of the hot spot formed at the core edge. In the context of energy deposition, the core plasma density is extremely high, reaching up to nearly
![]() $10^{26}~ {\rm cm}^{-3}$
(for mass density
$10^{26}~ {\rm cm}^{-3}$
(for mass density
![]() $300~ {\rm g}~ {\rm cm}^{-3}$
), and the energy loss mechanisms dominated by plasma collective behavior such as micro-instabilities during beam–plasma interaction, self-field generation and heating, etc., will be greatly or totally suppressed. Therefore, the fast electrons (ignitor) lose their energy mainly due to collisional process. Since the collision time between a fast electron and a core plasma particle is very fast, typically on the order of
$300~ {\rm g}~ {\rm cm}^{-3}$
), and the energy loss mechanisms dominated by plasma collective behavior such as micro-instabilities during beam–plasma interaction, self-field generation and heating, etc., will be greatly or totally suppressed. Therefore, the fast electrons (ignitor) lose their energy mainly due to collisional process. Since the collision time between a fast electron and a core plasma particle is very fast, typically on the order of
![]() $10^{-16}~ {\rm s}$
, this means that a kinetic approach will be of great necessity in order to gain more knowledge during energy deposition.
$10^{-16}~ {\rm s}$
, this means that a kinetic approach will be of great necessity in order to gain more knowledge during energy deposition.
Two kinds of collision type are involved in our Fokker–Planck code, namely, short-range and long-rang collisions. The former refers to the binary Coulomb collisions with impact parameter less than the Debye length; they are well described by the Fokker–Planck collision operator. The latter is associated with the collective response of core plasmas, which is often treated with the Balescu–Lenard collision term. These collision operators were simplified in an exact way. It should be noted that the authors of Ref. [Reference Yokota, Nakao, Johzaki and Mima51] had also tried to study energy deposition with a relativistic Fokker–Planck model, in which a simple and linearized collision term is obtained under a cold plasma approximation. In our model, the exact collision term was converted from an initial complex integrodifferential form to a differential expression with analogous Rosenbluth potential functions. The explicit expansion of potential functions in terms of spherical harmonics allowed us to rewrite the collision operator in a compact form which contains only simple integrations and differentiations, readily suitable for rapid numerical evaluation as well as analytic work. The corresponding Fokker–Planck code is developed and benchmarked physically. Several numerical techniques are developed to deal with the involved complexity of the relativistic Fokker–Planck model. The collisional coefficients is calculated with a multi-dimensional integration algorithm with high resolution. An implicit finite-volume method is adopted to recover the conservative properties of the kinetic equation and a nonlinear flux limiter is introduced to guarantee a non-negative distribution function.
Preliminary numerical studies on fast-electron energy deposition is made with our relativistic Fokker–Planck code. In the context of energy deposition, a collision generally has two effects on the incident fast electrons. On the one hand, it will cause a slowing down, leading to energy loss. On the other hand, it will scatter electrons to deviate from their initial incident direction, resulting in beam blooming. Two quantities are very important in evaluating the energy deposition profile, and they have been extensively studied by many other authors[Reference Solodov and Betti52]: the continuous path length before they are stopped (continuous range) and the depth it can reach along the initial direction (penetration depth). They can be obtained straightforwardly with Fokker–Planck code. Details can be found in Ref. [Reference Wu, Zhang, Zhou, Zhu and He50].
7. Discussion and summary
FI, which is considered to provide an alternative way of achieving ICF ignition with a considerably smaller laser energy, is being studied by many groups worldwide using ultra-intense short-pulse lasers. In the last ten years, it has opened new and very promising perspectives for relativistic laser–plasma interaction, and has made significant progress in understanding and improving ignition physics. However, there are still many issues associated with FI, such as inefficient laser–target energy coupling. It should be noted that the present low laser coupling efficiency is obtained from experiments on petawatt laser facilities with output energy smaller than 1 kJ and a pulse duration smaller than 1 ps. Actually, in FI, the laser beams have to deliver
![]() ${>}200~ {\rm kJ}$
in 20 ps. Since the laser energy and pulse duration play an important role in the generation of fast electrons, it is still hard to extend the physics from these hundreds-of-Joule laser facilities to a thousand times bigger one (200 kJ). Further efforts associated with this issue will be carried on in the future.
${>}200~ {\rm kJ}$
in 20 ps. Since the laser energy and pulse duration play an important role in the generation of fast electrons, it is still hard to extend the physics from these hundreds-of-Joule laser facilities to a thousand times bigger one (200 kJ). Further efforts associated with this issue will be carried on in the future.
In the IAPCM, significant progress in code developing and FI physics understanding has been achieved since the FI project was formally started in 2009. Reliable PIC code, hybrid PIC code, and radiation hydrodynamic code have been developed and checked. The physics of pellet compression, and the production, transportation, and deposition of fast electrons in overdense plasmas have been studied with our codes. In particular, a number of ideas to control the beam divergence of the fast electrons have been described with our PIC code and hybrid PIC codes. Furthermore, the FI target design has been carried out with our hydrodynamic code and demonstrated in the experiments on Shenguang series laser facilities. As the next step, the coupling efficiency of FI will be investigated with our integrated simulation codes and the Shenguang-II upgraded laser facility.
Acknowledgements
The authors gratefully acknowledge C. Y. Zheng, Z. J. Liu for fruitful discussions. This work was supported by the National Natural Science Foundation of China (Grant Nos. 11275028, 11105016 and 91230205).