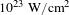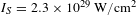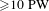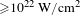1 Introduction
Scientists and engineers use Einstein’s famous energy–mass equivalence,
![]() $E=mc^{2}$
, to calculate the transformation of part of the mass of nuclei into energy by nuclear fission or fusion reactions (via differences in the rest mass energy when large nuclei are split or small nuclei combined). Quantum electrodynamics (QED) predicts that the reverse can also be achieved: transforming the energy of the laser photons into mass, via the generation of electron–positron pairs. Nevertheless, the QED effect like electron–positron avalanche pair production to appear spontaneously from vacuum requires a very high, Schwinger electric field[Reference Schwinger1] of
$E=mc^{2}$
, to calculate the transformation of part of the mass of nuclei into energy by nuclear fission or fusion reactions (via differences in the rest mass energy when large nuclei are split or small nuclei combined). Quantum electrodynamics (QED) predicts that the reverse can also be achieved: transforming the energy of the laser photons into mass, via the generation of electron–positron pairs. Nevertheless, the QED effect like electron–positron avalanche pair production to appear spontaneously from vacuum requires a very high, Schwinger electric field[Reference Schwinger1] of
![]() $E_{S}=1.3\times 10^{16}~\text{V}/\text{cm}$
. This would require focusing a high power laser to very high Schwinger intensity of
$E_{S}=1.3\times 10^{16}~\text{V}/\text{cm}$
. This would require focusing a high power laser to very high Schwinger intensity of
![]() $I_{S}=2.3\times 10^{29}~\text{W}/\text{cm}^{2}$
. The problem is that the Schwinger intensity is significantly larger than the intensities experimentally achievable even with the new, extremely powerful laser facilities under construction[Reference Danson, Hillier, Hopps and Neely2] like, for example, a
$I_{S}=2.3\times 10^{29}~\text{W}/\text{cm}^{2}$
. The problem is that the Schwinger intensity is significantly larger than the intensities experimentally achievable even with the new, extremely powerful laser facilities under construction[Reference Danson, Hillier, Hopps and Neely2] like, for example, a
![]() $2\times 10$
petawatt (PW),
$2\times 10$
petawatt (PW),
![]() $I>10^{22}~\text{W}/\text{cm}^{2}$
facility[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3–Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5] and a 100 PW,
$I>10^{22}~\text{W}/\text{cm}^{2}$
facility[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3–Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5] and a 100 PW,
![]() $I>10^{23}~\text{W}/\text{cm}^{2}$
facility[Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6]. Engineering and construction of such ultra-powerful, femtosecond, lasers is made possible by the discovery of the chirped pulse amplification (CPA) technique by Strickland and Mourou[Reference Strickland and Mourou7] which was rewarded with a share in the 2018 Nobel Prize in Physics. Mourou went on to champion the construction of the extreme light infrastructure (ELI) in Europe as well as other such facilities worldwide, pushing the power of the laser pulses to the extreme towards the high field physics regime. While even the planned lasers ultra-high intensities will still be much lower than
$I>10^{23}~\text{W}/\text{cm}^{2}$
facility[Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6]. Engineering and construction of such ultra-powerful, femtosecond, lasers is made possible by the discovery of the chirped pulse amplification (CPA) technique by Strickland and Mourou[Reference Strickland and Mourou7] which was rewarded with a share in the 2018 Nobel Prize in Physics. Mourou went on to champion the construction of the extreme light infrastructure (ELI) in Europe as well as other such facilities worldwide, pushing the power of the laser pulses to the extreme towards the high field physics regime. While even the planned lasers ultra-high intensities will still be much lower than
![]() $I_{S}$
, this could be overcome by using the geometry of colliding two PW laser pulses: (a) the first PW laser pulse accelerates an electron bunch to relativistic energies of several GeV/electron, using either gas or solid targets; and (b) the second PW laser pulse is focused to the maximum intensity on the relativistic electron bunch in order to generate the QED effects. The relativistic electron experiences a much larger electric field in its own frame of reference than the actual laser electric field in the laboratory frame of reference. QED effects predicted by theory and under experimental investigation are: (a) nonlinear, multiphoton, inverse Compton scattering; (b) radiation reaction; (c) electron-positron pair production; (d) vacuum birefringence. The first three processes are presented as a cartoon in Figure 1.
$I_{S}$
, this could be overcome by using the geometry of colliding two PW laser pulses: (a) the first PW laser pulse accelerates an electron bunch to relativistic energies of several GeV/electron, using either gas or solid targets; and (b) the second PW laser pulse is focused to the maximum intensity on the relativistic electron bunch in order to generate the QED effects. The relativistic electron experiences a much larger electric field in its own frame of reference than the actual laser electric field in the laboratory frame of reference. QED effects predicted by theory and under experimental investigation are: (a) nonlinear, multiphoton, inverse Compton scattering; (b) radiation reaction; (c) electron-positron pair production; (d) vacuum birefringence. The first three processes are presented as a cartoon in Figure 1.
Examples of new laser facilities under construction with interaction chambers dedicated to QED experiments are: extreme light infrastructure – nuclear physics (ELI-NP)[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3–Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5]
![]() $2\times 10~\text{PW}$
laser beams in Romania and the Station of Extreme Light (SEL)[Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6] 100 PW laser beam and 10 keV XFEL beam at the ‘Shanghai HIgh repetition rate XFEL aNd Extreme light facility (SHINE)’ in China. The ELI-NP interaction chambers E6 and E1 are designed to interact two colliding 10 PW laser pulses in gas targets and solid targets, respectively[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3, Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Balascuta, Cappuzzello, Cernaianu, Chen, Dancus, Freeman, Geissel, Genuche, Gizzi, Gobet, Gosselin, Gugiu, Higginson, D’humières, Ivan, Jaroszynski, Kar, Lamia, Leca, Neagu, Lanzalone, Méot, Mirfayzi, Mitu, Morel, Murphy, Petcu, Petrascu, Petrone, Raczka, Risca, Rotaru, Santos, Schumacher, Stutman, Tarisien, Tataru, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir4, Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6]. The SEL interaction chamber is designed for a tightly focused 100 PW pulse in vacuum with the 10 keV XFEL pulse probing the induced vacuum birefringence[Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6]. There are proposals for providing a second PW beam in order to perform QED experiments with colliding PW pulses.
$2\times 10~\text{PW}$
laser beams in Romania and the Station of Extreme Light (SEL)[Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6] 100 PW laser beam and 10 keV XFEL beam at the ‘Shanghai HIgh repetition rate XFEL aNd Extreme light facility (SHINE)’ in China. The ELI-NP interaction chambers E6 and E1 are designed to interact two colliding 10 PW laser pulses in gas targets and solid targets, respectively[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3, Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Balascuta, Cappuzzello, Cernaianu, Chen, Dancus, Freeman, Geissel, Genuche, Gizzi, Gobet, Gosselin, Gugiu, Higginson, D’humières, Ivan, Jaroszynski, Kar, Lamia, Leca, Neagu, Lanzalone, Méot, Mirfayzi, Mitu, Morel, Murphy, Petcu, Petrascu, Petrone, Raczka, Risca, Rotaru, Santos, Schumacher, Stutman, Tarisien, Tataru, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir4, Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6]. The SEL interaction chamber is designed for a tightly focused 100 PW pulse in vacuum with the 10 keV XFEL pulse probing the induced vacuum birefringence[Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6]. There are proposals for providing a second PW beam in order to perform QED experiments with colliding PW pulses.
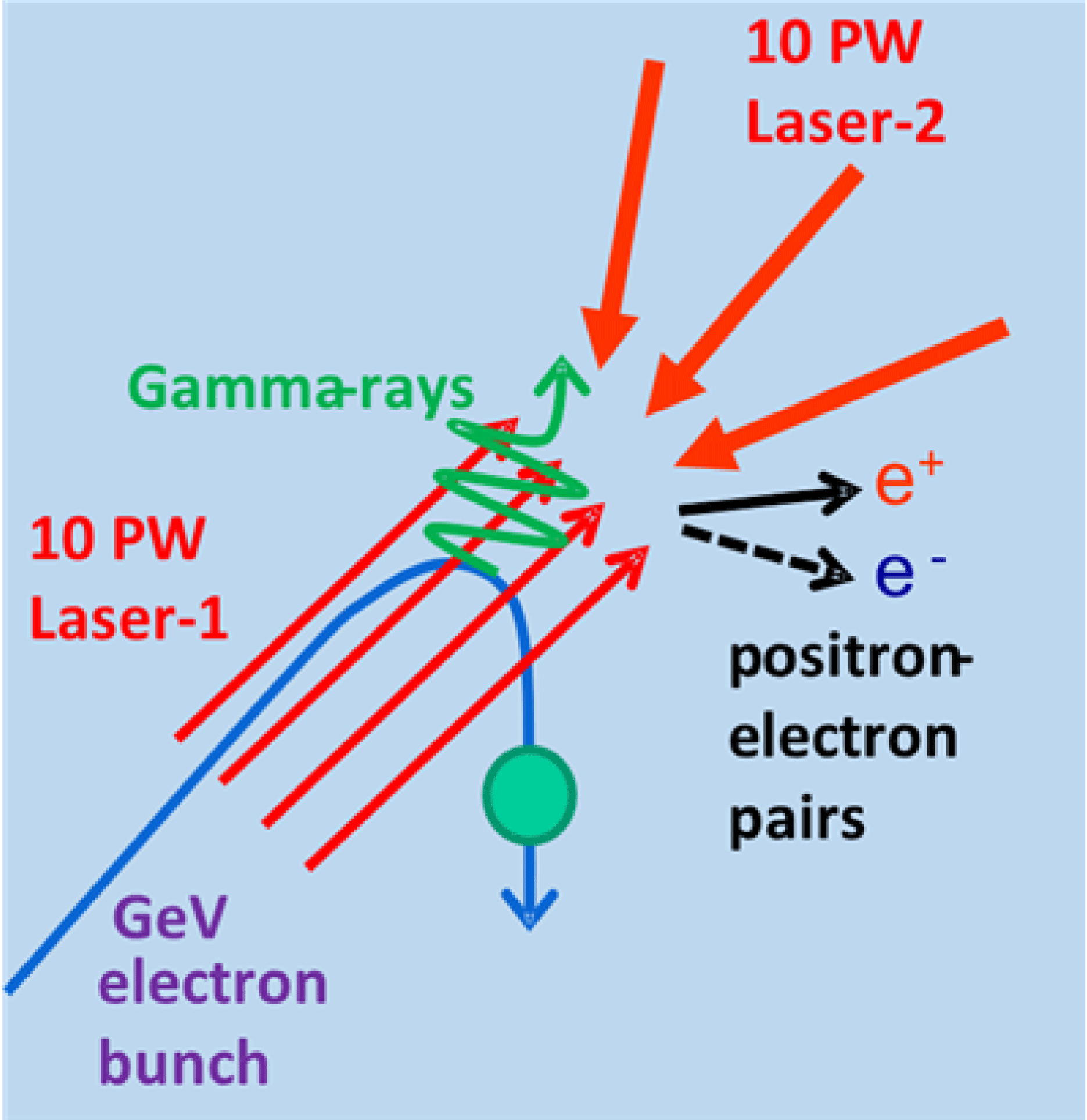
Figure 1. High field processes schematic cartoon: radiation-reaction (RR) slowing of the electrons, nonlinear (multiphoton) inverse Compton generation of Gamma rays, multiphoton Breit–Wheeler electron–positron pair production. (Courtesy PMcK.)
Recently, experimental evidence was reported[Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8, Reference Poder, Tamburini, Sarri, Di Piazza, Kuschel, Baird, Behm, Bohlen, Cole, Corvan, Duff, Gerstmayr, Keitel, Krushelnick, Mangles, McKenna, Murphy, Najmudin, Ridgers, Samarin, Symes, Thomas, Warwick and Zepf9] of relativistic electron radiation reaction (RR) generation in the field of the second colliding laser with an intensity of
![]() $I=4\times 10^{20}~\text{W}/\text{cm}^{2}$
. The experiments were performed by a collaboration led by the Queen’s University Belfast and Imperial College London using the Astra Gemini PW, 2-Beam Laser[Reference Hooker, Collier, Chekhlov, Clarke, Divall, Ertel, Fell, Foster, Hancock, Langley, Neely and Smith10] at the Central Laser Facility in the UK.
$I=4\times 10^{20}~\text{W}/\text{cm}^{2}$
. The experiments were performed by a collaboration led by the Queen’s University Belfast and Imperial College London using the Astra Gemini PW, 2-Beam Laser[Reference Hooker, Collier, Chekhlov, Clarke, Divall, Ertel, Fell, Foster, Hancock, Langley, Neely and Smith10] at the Central Laser Facility in the UK.
Theoretical studies of colliding laser beams in solid and near-critical plasmas at intensities of
![]() $10^{22}~\text{W}/\text{cm}^{2}$
,
$10^{22}~\text{W}/\text{cm}^{2}$
,
![]() $10^{23}~\text{W}/\text{cm}^{2}$
and even
$10^{23}~\text{W}/\text{cm}^{2}$
and even
![]() $10^{24}~\text{W}/\text{cm}^{2}$
predict efficient conversion of laser energy into dense electron–positron pairs and bursts of energetic Gamma rays[Reference Zhu, Yu, Sheng, Yin, Turcu and Pukhov11–Reference Luo, Wu, Liu, Ma, Li, Yuan, Yu, Chen and Sheng20].
$10^{24}~\text{W}/\text{cm}^{2}$
predict efficient conversion of laser energy into dense electron–positron pairs and bursts of energetic Gamma rays[Reference Zhu, Yu, Sheng, Yin, Turcu and Pukhov11–Reference Luo, Wu, Liu, Ma, Li, Yuan, Yu, Chen and Sheng20].
2 High field physics, QED processes with colliding PW laser pulses
Important processes in ultra-high laser fields are in Refs.[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3, Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Balascuta, Cappuzzello, Cernaianu, Chen, Dancus, Freeman, Geissel, Genuche, Gizzi, Gobet, Gosselin, Gugiu, Higginson, D’humières, Ivan, Jaroszynski, Kar, Lamia, Leca, Neagu, Lanzalone, Méot, Mirfayzi, Mitu, Morel, Murphy, Petcu, Petrascu, Petrone, Raczka, Risca, Rotaru, Santos, Schumacher, Stutman, Tarisien, Tataru, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir4] and references therein.
(1) Nonlinear, multiphoton, inverse Compton scattering in which up to 40% of the energy of the laser accelerated electrons is re-radiated as Gamma-ray photons in the presence of the laser field:
(1)where the electron, $$\begin{eqnarray}e^{-}+m(h\unicode[STIX]{x1D708})_{L}\rightarrow e^{-}+(h\unicode[STIX]{x1D708})_{GR},\end{eqnarray}$$
$$\begin{eqnarray}e^{-}+m(h\unicode[STIX]{x1D708})_{L}\rightarrow e^{-}+(h\unicode[STIX]{x1D708})_{GR},\end{eqnarray}$$
 $e^{-}$
, absorbs multiple,
$e^{-}$
, absorbs multiple,
 $m$
, laser photons,
$m$
, laser photons,
 $(h\unicode[STIX]{x1D708})_{L}$
, and radiates hard Gamma-ray photons,
$(h\unicode[STIX]{x1D708})_{L}$
, and radiates hard Gamma-ray photons,
 $(h\unicode[STIX]{x1D708})_{GR}$
.
$(h\unicode[STIX]{x1D708})_{GR}$
.(2) RR in which the accelerated electron recoils from the emission of the high energy Gamma-ray photon.
(3) Electron–positron pair production by the multiphoton Breit–Wheeler (BW) process:
(2)where the electron, $$\begin{eqnarray}(h\unicode[STIX]{x1D708})_{GR}+m(h\unicode[STIX]{x1D708})_{L}\rightarrow e^{-}+\,e^{+},\end{eqnarray}$$
$$\begin{eqnarray}(h\unicode[STIX]{x1D708})_{GR}+m(h\unicode[STIX]{x1D708})_{L}\rightarrow e^{-}+\,e^{+},\end{eqnarray}$$
 $e^{-}$
, positron,
$e^{-}$
, positron,
 $e^{+}$
, pair is generated. Hence for the energy of multiple laser photons, pure energy is transformed into the mass of the particles: electrons and positrons. Light is transformed into matter.
$e^{+}$
, pair is generated. Hence for the energy of multiple laser photons, pure energy is transformed into the mass of the particles: electrons and positrons. Light is transformed into matter.
The parameter
![]() $\unicode[STIX]{x1D712}$
determines the importance of strong-field QED effects[Reference Ritus21–Reference Di Piazza, Müller, Hatsagortsyan and Keitel23] and the reaction rate of these processes becomes important when
$\unicode[STIX]{x1D712}$
determines the importance of strong-field QED effects[Reference Ritus21–Reference Di Piazza, Müller, Hatsagortsyan and Keitel23] and the reaction rate of these processes becomes important when
![]() $\unicode[STIX]{x1D712}\rightarrow 1$
with
$\unicode[STIX]{x1D712}\rightarrow 1$
with
where
![]() $\unicode[STIX]{x1D6FE}$
is the Lorentz factor of relativistic electrons,
$\unicode[STIX]{x1D6FE}$
is the Lorentz factor of relativistic electrons,
![]() $\unicode[STIX]{x1D703}$
is the ‘geometric factor’ which takes account of the angle between the electric field and the electron momentum,
$\unicode[STIX]{x1D703}$
is the ‘geometric factor’ which takes account of the angle between the electric field and the electron momentum,
![]() $I_{L}$
is the focused laser intensity and
$I_{L}$
is the focused laser intensity and
![]() $I_{S}=2.3\times 10^{29}~\text{W}/\text{cm}^{2}$
is the Schwinger intensity at which spontaneous generation of electron–positron pairs from vacuum occurs.
$I_{S}=2.3\times 10^{29}~\text{W}/\text{cm}^{2}$
is the Schwinger intensity at which spontaneous generation of electron–positron pairs from vacuum occurs.

Figure 2. Quantum electrodynamics with colliding PW laser pulses. First focused PW laser pulse accelerates electrons to relativistic energies from gas targets (left panel) and solid targets (right panel). Second tightly focused PW laser pulse provides the ultra-intense electromagnetic field. The relativistic electrons travel through this ultra-intense field generating QED effects. (Courtesy X.-L. Zhu and T.-P. Yu.)
While laser technology is continuously increasing
![]() $I_{L}$
, in the medium term
$I_{L}$
, in the medium term
![]() $I_{L}/I_{S}\ll 1$
. Nevertheless, in order to achieve
$I_{L}/I_{S}\ll 1$
. Nevertheless, in order to achieve
![]() $\unicode[STIX]{x1D712}\rightarrow 1$
, we can experimentally maximize:
$\unicode[STIX]{x1D712}\rightarrow 1$
, we can experimentally maximize:
(a) the Lorentz factor,
 $\unicode[STIX]{x1D6FE}$
, by accelerating electrons to ultra-relativistic energies, and
$\unicode[STIX]{x1D6FE}$
, by accelerating electrons to ultra-relativistic energies, and(b) the ‘geometric factor’,
 $\unicode[STIX]{x1D703}$
, by colliding two counter-propagating PW laser pulses.
$\unicode[STIX]{x1D703}$
, by colliding two counter-propagating PW laser pulses.
Maximizing
![]() $\unicode[STIX]{x1D712}$
, by maximizing
$\unicode[STIX]{x1D712}$
, by maximizing
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D703}$
can be achieved by colliding two PW laser pulses as shown in Figure 2.
$\unicode[STIX]{x1D703}$
can be achieved by colliding two PW laser pulses as shown in Figure 2.
(1) The first focused PW laser pulse accelerates electrons to relativistic energies from a gas target or a solid target.
(2) The second tightly focused PW laser pulse provides the ultra-intense electromagnetic field in its focus. The relativistic electrons accelerated by the ‘first PW pulse’ travel through the focus of the ‘second PW pulse’, are immersed in this ultra-intense electromagnetic field and generate the QED effects resulting in copious Gamma-photon and electron–positron pair production.
(3) The relativistic Lorentz factor,
 $\unicode[STIX]{x1D6FE}$
, is very large in the case of gas targets, but the number of relativistic electrons in the pulse is lower than that in the case of solid targets. While we have a large number of relativistic electrons in the pulse generated in solid targets, the Lorentz factor
$\unicode[STIX]{x1D6FE}$
, is very large in the case of gas targets, but the number of relativistic electrons in the pulse is lower than that in the case of solid targets. While we have a large number of relativistic electrons in the pulse generated in solid targets, the Lorentz factor
 $\unicode[STIX]{x1D6FE}$
is lower.
$\unicode[STIX]{x1D6FE}$
is lower.
3 ELI-NP 2
 $\times$
10 PW colliding pulses facility for QED experiments
$\times$
10 PW colliding pulses facility for QED experiments
The ELI-NP facility in Romania has a unique laser system for colliding 10 PW laser pulses[Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5]. Figure 3 shows the layout of the CPA titanium:sapphire laser system from Thales Optronique, France. The laser system has two identical laser amplifier arms which provide 10 PW laser pulses each. The two 10 PW laser pulses are seeded from the same laser oscillator pulse which is split into two and the two resulting pulses are amplified in the two amplifier chains. Therefore the two 10 PW pulses are naturally synchronized. While the two amplifier chains are identical, there will still be variations in the optical path travelled by the pulses in the two chains. Therefore additional care needs to be taken for ‘femtosecond’ level synchronization, as described in Section 6.

Figure 3. Unique CPA titanium:sapphire laser system for colliding 10 PW laser pulses. ELI-NP laser system has two laser amplifier arms which provide 10 PW laser pulses each: (a) the two 10 PW laser pulses are seeded from the same laser oscillator pulse; (b) the two focused 10 PW laser pulses collide in any of the three interaction chambers: E1, E6 and E7 (E7 bunker is south of E6 and E1 and is not shown in figure). (Courtesy ELI-NP, Romania and Thales Optronique, France.)
Each 10 PW laser pulse will have energy of
![]() ${\sim}200$
J/pulse and pulse duration of
${\sim}200$
J/pulse and pulse duration of
![]() ${\sim}20$
fs. The beams will be nearly diffraction limited with a Strehl ratio of 0.9. The laser intensity contrast above pre-pulses will be very high:
${\sim}20$
fs. The beams will be nearly diffraction limited with a Strehl ratio of 0.9. The laser intensity contrast above pre-pulses will be very high:
![]() $10^{-13}/100~\text{ps}$
,
$10^{-13}/100~\text{ps}$
,
![]() $10^{-9}/10~\text{ps}$
and
$10^{-9}/10~\text{ps}$
and
![]() $10^{-7}/5~\text{ps}$
. These properties are highly desirable for focusing to ultra-high intensity on solid targets. The laser system will have a high pulse repetition rate of 1 pulse/min for the
$10^{-7}/5~\text{ps}$
. These properties are highly desirable for focusing to ultra-high intensity on solid targets. The laser system will have a high pulse repetition rate of 1 pulse/min for the
![]() $2\times 10~\text{PW}$
pulses. The laser beam cross section will be large:
$2\times 10~\text{PW}$
pulses. The laser beam cross section will be large:
![]() ${\sim}55$
cm diameter. The
${\sim}55$
cm diameter. The
![]() $2\times 10~\text{PW}$
pulses will be directed into the interaction areas. A laser beam delivery system[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3–Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5] will provide a switchyard for the two 10 PW pulses to be directed to any of the three interaction chambers, E1, E6 and E7 as shown in Figure 4.
$2\times 10~\text{PW}$
pulses will be directed into the interaction areas. A laser beam delivery system[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3–Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5] will provide a switchyard for the two 10 PW pulses to be directed to any of the three interaction chambers, E1, E6 and E7 as shown in Figure 4.

Figure 4. Unique facility for QED with colliding 10 PW focused laser pulses at ELI-NP[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3–Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5]. The focused
![]() $2\times 10~\text{PW}$
laser pulses will collide in any of the three interaction chambers: E1, E6 and E7. E6 interaction chamber is dedicated to QED experiments with
$2\times 10~\text{PW}$
laser pulses will collide in any of the three interaction chambers: E1, E6 and E7. E6 interaction chamber is dedicated to QED experiments with
![]() $f=30$
m long focal length mirror for wake-field electron acceleration from gas targets and F/4 mirror providing tight focus with ultra-intense EM fields. E1 interaction chamber is dedicated to nuclear physics experiments with solid targets: two F/3 mirrors providing tight focus with ultra-intense EM fields. This configuration will also be used for colliding laser pulses QED experiments with solid targets. E7 interaction chamber is dedicated to experiments with two colliding 10 PW focused laser pulses combined with Gamma pulses as probe. The Gamma pulses will be generated from an inverse Compton scattering interaction of an additional laser focused on relativistic electron bunches generated in an additional linear accelerator. (Courtesy ELI-NP, Romania.)
$f=30$
m long focal length mirror for wake-field electron acceleration from gas targets and F/4 mirror providing tight focus with ultra-intense EM fields. E1 interaction chamber is dedicated to nuclear physics experiments with solid targets: two F/3 mirrors providing tight focus with ultra-intense EM fields. This configuration will also be used for colliding laser pulses QED experiments with solid targets. E7 interaction chamber is dedicated to experiments with two colliding 10 PW focused laser pulses combined with Gamma pulses as probe. The Gamma pulses will be generated from an inverse Compton scattering interaction of an additional laser focused on relativistic electron bunches generated in an additional linear accelerator. (Courtesy ELI-NP, Romania.)
The E6 interaction chamber at ELI-NP is dedicated to QED experiments with two counter-propagating, focused, colliding 10 PW laser pulses in gas targets[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3–Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5] as shown in Figure 4. The long focal length mirror, F/50, will focus the ‘first’ 10 PW pulse (pictured ‘red’ in Figure 4) on gas targets accelerating the electron bunch to ultra-relativistic energies. Electron energies well in excess of 10 GeV are predicted. The short focal length F/4 mirror will focus the ‘second’ 10 PW pulse (pictured ‘blue’ in Figure 4) to a tight focus in front of the gas target. Ultra-high intensities in excess of
![]() $I>10^{22}~\text{W}/\text{cm}^{2}$
are expected. The ultra-relativistic electrons accelerated by the ‘first 10 PW pulse’ will travel through the focus of the ‘second 10 PW pulse’ where they will be immersed in this ultra-intense,
$I>10^{22}~\text{W}/\text{cm}^{2}$
are expected. The ultra-relativistic electrons accelerated by the ‘first 10 PW pulse’ will travel through the focus of the ‘second 10 PW pulse’ where they will be immersed in this ultra-intense,
![]() $I>10^{22}~\text{W}/\text{cm}^{2}$
, electromagnetic field and generate the QED effects resulting in Gamma photons and electron–positron pair production. The electrons and positron energy spectra will be measured with spectrometers. The hard Gamma photons will be measured with Gamma detector placed inside the electron ‘beam-dump’ in order to improve the signal-to-noise ratio.
$I>10^{22}~\text{W}/\text{cm}^{2}$
, electromagnetic field and generate the QED effects resulting in Gamma photons and electron–positron pair production. The electrons and positron energy spectra will be measured with spectrometers. The hard Gamma photons will be measured with Gamma detector placed inside the electron ‘beam-dump’ in order to improve the signal-to-noise ratio.
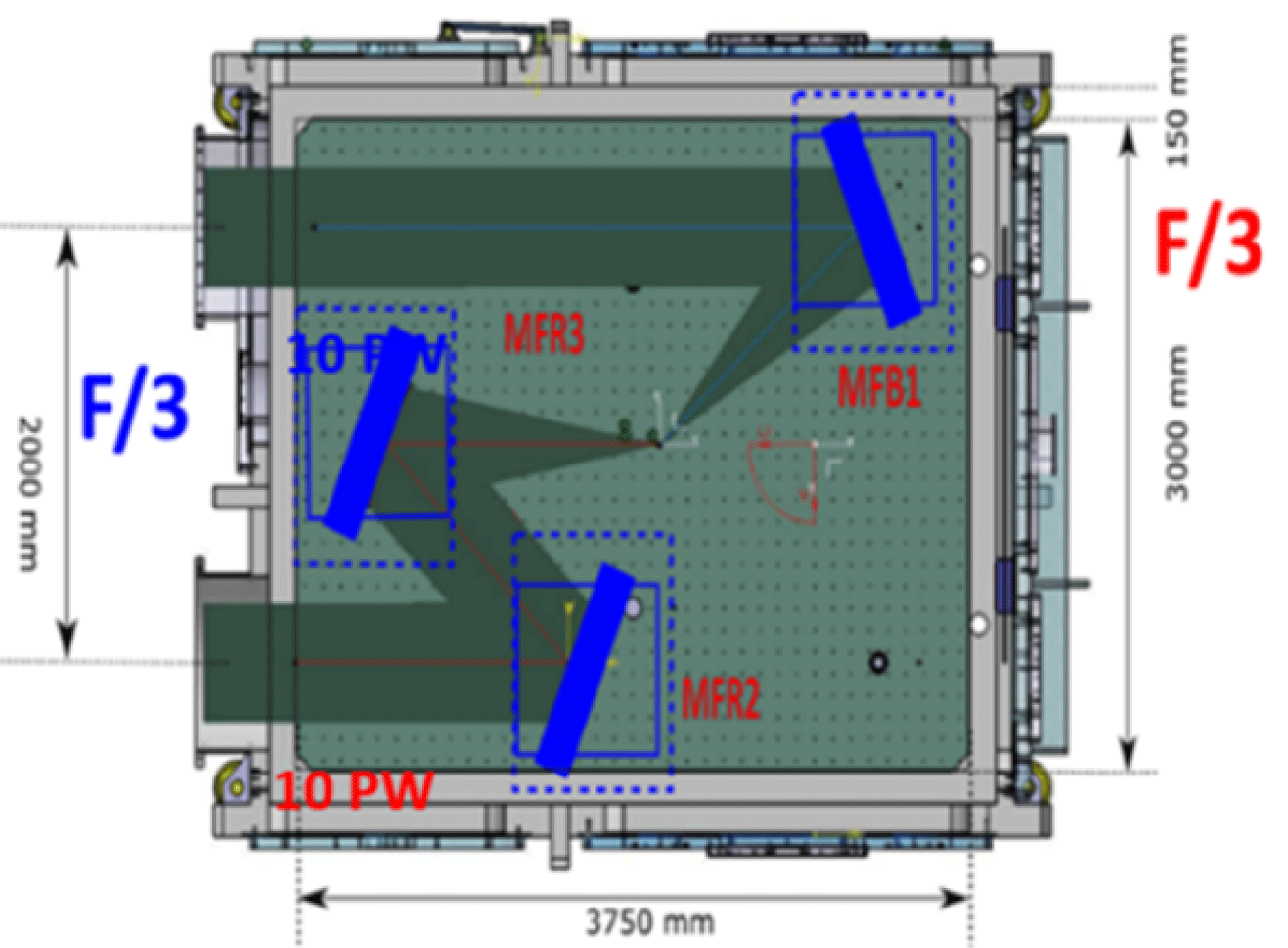
Figure 5. The
![]() $2\times 10~\text{PW}$
laser pulses will collide in the E1 interaction chamber of ELI-NP, which is dedicated to nuclear physics experiments with solid targets[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3–Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5]. The two laser pulses will be brought to a tight focus with two F/3 mirrors. E1 chamber will also be used for QED colliding pulse experiments with solid foil targets. (Courtesy ELI-NP, Romania.)
$2\times 10~\text{PW}$
laser pulses will collide in the E1 interaction chamber of ELI-NP, which is dedicated to nuclear physics experiments with solid targets[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3–Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5]. The two laser pulses will be brought to a tight focus with two F/3 mirrors. E1 chamber will also be used for QED colliding pulse experiments with solid foil targets. (Courtesy ELI-NP, Romania.)
The E1 interaction chamber at ELI-NP is dedicated to nuclear physics experiments with one or two 10 PW pulses focused with short focal length mirrors on solid targets[Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Balascuta, Cappuzzello, Cernaianu, Chen, Dancus, Freeman, Geissel, Genuche, Gizzi, Gobet, Gosselin, Gugiu, Higginson, D’humières, Ivan, Jaroszynski, Kar, Lamia, Leca, Neagu, Lanzalone, Méot, Mirfayzi, Mitu, Morel, Murphy, Petcu, Petrascu, Petrone, Raczka, Risca, Rotaru, Santos, Schumacher, Stutman, Tarisien, Tataru, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir4, Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5]. QED experiments with solid targets will be carried out in the E1 chamber with two counter-propagating, focused, colliding 10 PW laser pulses[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3–Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5] as shown in Figures 4 and 5. The two short focal length F/3 mirrors will focus each of the
![]() $2\times 10~\text{PW}$
pulses to a tight focus on either side of the thin foil solid target. Ultra-high intensities in excess of
$2\times 10~\text{PW}$
pulses to a tight focus on either side of the thin foil solid target. Ultra-high intensities in excess of
![]() $I>10^{22}~\text{W}/\text{cm}^{2}$
are expected. The high-density, solid-density, relativistic electrons accelerated by the ‘first 10 PW pulse’ will travel through the focus of the ‘second 10 PW pulse’ where they will be immersed in this ultra-intense,
$I>10^{22}~\text{W}/\text{cm}^{2}$
are expected. The high-density, solid-density, relativistic electrons accelerated by the ‘first 10 PW pulse’ will travel through the focus of the ‘second 10 PW pulse’ where they will be immersed in this ultra-intense,
![]() $I>10^{22}~\text{W}/\text{cm}^{2}$
, electromagnetic field and will generate QED effects resulting in Gamma photons and electron–positron pair production. Additional ‘plasma mirror’[Reference Ziener, Foster, Divall, Hooker, Hutchinson, Langley and Neely24] can be added in the focusing geometry to further increase the intensity contrast of the laser pulse at the focal spot[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3–Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5].
$I>10^{22}~\text{W}/\text{cm}^{2}$
, electromagnetic field and will generate QED effects resulting in Gamma photons and electron–positron pair production. Additional ‘plasma mirror’[Reference Ziener, Foster, Divall, Hooker, Hutchinson, Langley and Neely24] can be added in the focusing geometry to further increase the intensity contrast of the laser pulse at the focal spot[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3–Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5].
4 Radiation-reaction measurements with two colliding pulses at Astra Gemini PW facility
Experimental evidence of RR QED effect with colliding laser pulses has been obtained in two experiments carried out by the collaboration led by the Queen’s University Belfast–Imperial College London[Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8, Reference Poder, Tamburini, Sarri, Di Piazza, Kuschel, Baird, Behm, Bohlen, Cole, Corvan, Duff, Gerstmayr, Keitel, Krushelnick, Mangles, McKenna, Murphy, Najmudin, Ridgers, Samarin, Symes, Thomas, Warwick and Zepf9] using the two-beam Astra Gemini PW-class Laser Facility[Reference Hooker, Collier, Chekhlov, Clarke, Divall, Ertel, Fell, Foster, Hancock, Langley, Neely and Smith10] at the STFC Central Laser Facility in UK. Figure 6 shows one of the two experimental configurations[Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8].
In the first experiment[Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8] the electron acceleration ‘driving laser pulse’ has
![]() $10~\text{J}/\text{pulse}$
, 45 fs pulse duration and is focused with an F/40 mirror to an intensity of
$10~\text{J}/\text{pulse}$
, 45 fs pulse duration and is focused with an F/40 mirror to an intensity of
![]() $I=7.7\times 10^{18}~\text{W}/\text{cm}^{2}$
and
$I=7.7\times 10^{18}~\text{W}/\text{cm}^{2}$
and
![]() $a_{0}=1.9$
on the gas jet. The energy of the accelerated electrons is
$a_{0}=1.9$
on the gas jet. The energy of the accelerated electrons is
![]() ${\sim}600~\text{MeV}$
. The ‘scattering laser pulse’ providing the high field has
${\sim}600~\text{MeV}$
. The ‘scattering laser pulse’ providing the high field has
![]() $8.6~\text{J}/\text{pulse}$
, 45 fs pulse duration and is focused with an F/2 mirror to
$8.6~\text{J}/\text{pulse}$
, 45 fs pulse duration and is focused with an F/2 mirror to
![]() $I=4\times 10^{20}~\text{W}/\text{cm}^{2}$
and
$I=4\times 10^{20}~\text{W}/\text{cm}^{2}$
and
![]() $a_{0}\sim 10$
at collision, and the parameter
$a_{0}\sim 10$
at collision, and the parameter
![]() $\unicode[STIX]{x1D712}$
is
$\unicode[STIX]{x1D712}$
is
![]() ${\sim}0.1$
. The two colliding laser pulses are synchronized to a precision of
${\sim}0.1$
. The two colliding laser pulses are synchronized to a precision of
![]() $\pm 30~\text{fs}$
(see Section 6). Use of gas jet target allowed collision close to exit of wake-field accelerator, where the electron beam is smaller than the laser beam and therefore detailed knowledge of the electron beam and laser profile is not needed. The relativistic electron bunch with a maximum energy of
$\pm 30~\text{fs}$
(see Section 6). Use of gas jet target allowed collision close to exit of wake-field accelerator, where the electron beam is smaller than the laser beam and therefore detailed knowledge of the electron beam and laser profile is not needed. The relativistic electron bunch with a maximum energy of
![]() ${\sim}0.6~\text{GeV}/\text{electron}$
propagates through the high field in the focus of the ‘scattering laser’ and generates hard Gamma photons through multiphoton inverse Compton scattering. The Gamma photons spectra are measured with Gamma spectrometer with CsI array. The electron spectra showing the mean energy loss after the high field interaction are measured with the magnetic electron spectrometer.
${\sim}0.6~\text{GeV}/\text{electron}$
propagates through the high field in the focus of the ‘scattering laser’ and generates hard Gamma photons through multiphoton inverse Compton scattering. The Gamma photons spectra are measured with Gamma spectrometer with CsI array. The electron spectra showing the mean energy loss after the high field interaction are measured with the magnetic electron spectrometer.
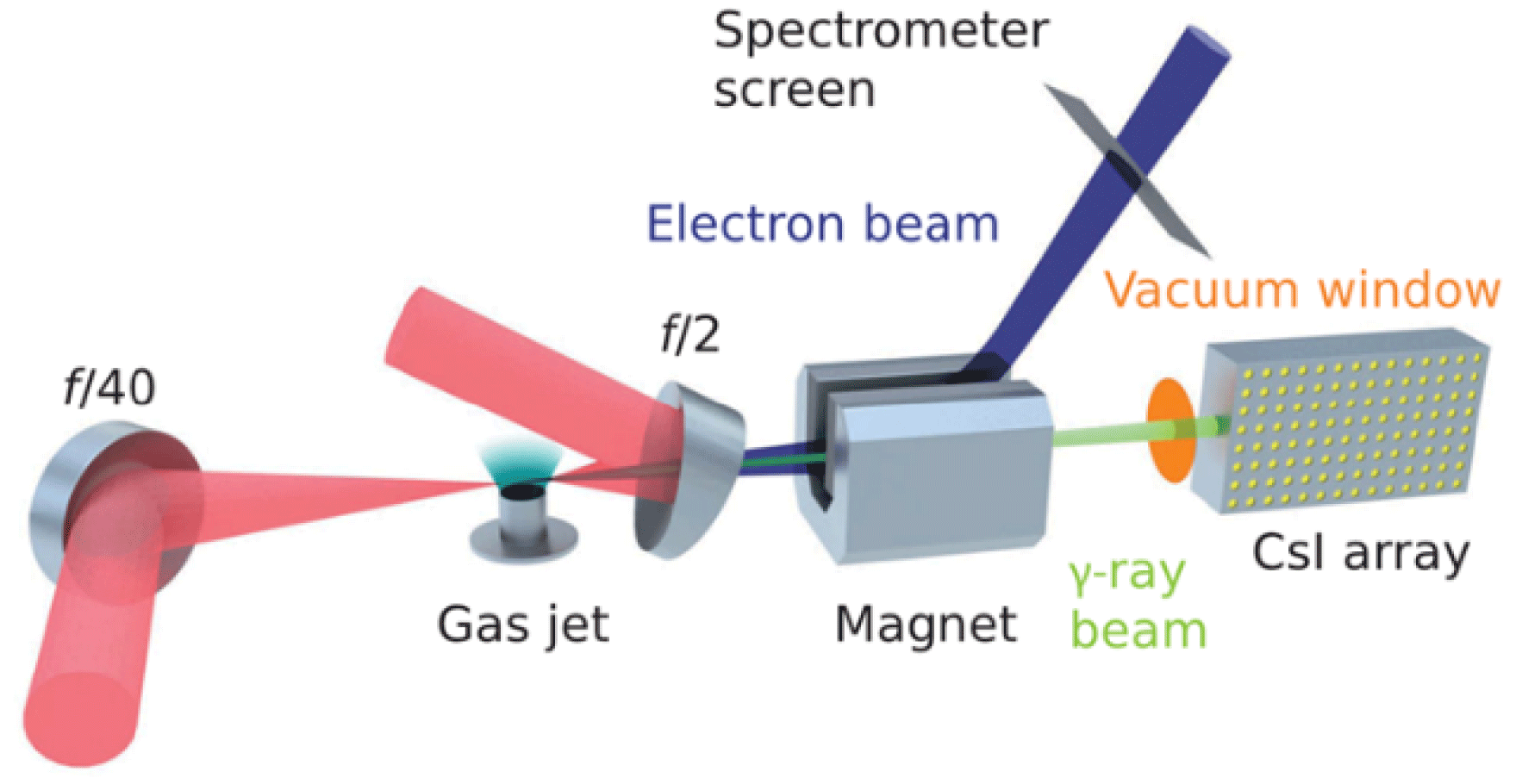
Figure 6. Experimental setup for measuring RR with colliding laser pulses by the Queen’s University Belfast–Imperial College London-led collaboration[Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6]. Driving laser:
![]() $10~\text{J}/45~\text{fs}$
, focused with F/40 mirror to
$10~\text{J}/45~\text{fs}$
, focused with F/40 mirror to
![]() $I=7.7\times 10^{18}~\text{W}/\text{cm}^{2}$
,
$I=7.7\times 10^{18}~\text{W}/\text{cm}^{2}$
,
![]() $a_{0}=1.9$
. Scattering laser:
$a_{0}=1.9$
. Scattering laser:
![]() $8.6~\text{J}/45~\text{fs}$
, focused with F/2 mirror to
$8.6~\text{J}/45~\text{fs}$
, focused with F/2 mirror to
![]() $I=4\times 10^{20}~\text{W}/\text{cm}^{2}$
,
$I=4\times 10^{20}~\text{W}/\text{cm}^{2}$
,
![]() $a_{0}\sim 10$
. Experiment used the 2-Beam Astra Gemini PW Laser Facility[Reference Hooker, Collier, Chekhlov, Clarke, Divall, Ertel, Fell, Foster, Hancock, Langley, Neely and Smith10] at STFC, Central Laser Facility, UK. (Courtesy the Queen’s University Belfast–Imperial College London-led collaboration[Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8, Reference Poder, Tamburini, Sarri, Di Piazza, Kuschel, Baird, Behm, Bohlen, Cole, Corvan, Duff, Gerstmayr, Keitel, Krushelnick, Mangles, McKenna, Murphy, Najmudin, Ridgers, Samarin, Symes, Thomas, Warwick and Zepf9]. Reproduced from Ref. [Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8].)
$a_{0}\sim 10$
. Experiment used the 2-Beam Astra Gemini PW Laser Facility[Reference Hooker, Collier, Chekhlov, Clarke, Divall, Ertel, Fell, Foster, Hancock, Langley, Neely and Smith10] at STFC, Central Laser Facility, UK. (Courtesy the Queen’s University Belfast–Imperial College London-led collaboration[Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8, Reference Poder, Tamburini, Sarri, Di Piazza, Kuschel, Baird, Behm, Bohlen, Cole, Corvan, Duff, Gerstmayr, Keitel, Krushelnick, Mangles, McKenna, Murphy, Najmudin, Ridgers, Samarin, Symes, Thomas, Warwick and Zepf9]. Reproduced from Ref. [Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8].)
Radiation-reaction effects were observed experimentally. Low-energy electron beams were observed on all successful collision shots as well as the correlation between the post-collision electron beam energy and the Gamma ray yield. The spectrum hard Gamma photons were measured, with energy
![]() $\unicode[STIX]{x1D700}_{\text{crit}}>30~\text{MeV}$
, which carried a significant fraction of the initial electron energy[Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8]. Good agreement was obtained between the experimental
$\unicode[STIX]{x1D700}_{\text{crit}}>30~\text{MeV}$
, which carried a significant fraction of the initial electron energy[Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8]. Good agreement was obtained between the experimental
![]() $a_{0}$
and
$a_{0}$
and
![]() $a_{0}$
derived from the electron and Gamma ray spectra under a quantum RR model. The data was compared with theoretical simulations utilizing different models, the quantum RR model, RR classical model, and a model without RR. The results are more consistent with quantum models of RR, but to measure differences between different quantum models, and a higher parameter
$a_{0}$
derived from the electron and Gamma ray spectra under a quantum RR model. The data was compared with theoretical simulations utilizing different models, the quantum RR model, RR classical model, and a model without RR. The results are more consistent with quantum models of RR, but to measure differences between different quantum models, and a higher parameter
![]() $\unicode[STIX]{x1D712}$
and measurements of the change in shape of the electron spectrum are needed.
$\unicode[STIX]{x1D712}$
and measurements of the change in shape of the electron spectrum are needed.
In the second experiment[Reference Poder, Tamburini, Sarri, Di Piazza, Kuschel, Baird, Behm, Bohlen, Cole, Corvan, Duff, Gerstmayr, Keitel, Krushelnick, Mangles, McKenna, Murphy, Najmudin, Ridgers, Samarin, Symes, Thomas, Warwick and Zepf9] the electron energy was significantly higher, extending to 2 GeV, and the use of gas cell target resulted in a more stable spectrum. The collision took place still at
![]() $a_{0}=10$
but due to the use of the gas cell, the collision occurs downstream, where the electron beam is in similar size to laser beam. In this case the electron beam profile effects become important. While crossing the ultra-high field region, the electrons see, in their own frame of reference, a field as high as
$a_{0}=10$
but due to the use of the gas cell, the collision occurs downstream, where the electron beam is in similar size to laser beam. In this case the electron beam profile effects become important. While crossing the ultra-high field region, the electrons see, in their own frame of reference, a field as high as
![]() $0.25I_{S}$
, where
$0.25I_{S}$
, where
![]() $I_{S}=2.3\times 10^{29}~\text{W}/\text{cm}^{2}$
is the Schwinger intensity. The ultra-relativistic electrons lose
$I_{S}=2.3\times 10^{29}~\text{W}/\text{cm}^{2}$
is the Schwinger intensity. The ultra-relativistic electrons lose
![]() ${>}$
30% of their energy when they emit Gamma rays during their interaction with the ultra-high field in the focus of the ‘scattering laser’. When compared with theoretical simulations, the change in shape of the electron spectrum is most consistent with the semiclassical RR model.
${>}$
30% of their energy when they emit Gamma rays during their interaction with the ultra-high field in the focus of the ‘scattering laser’. When compared with theoretical simulations, the change in shape of the electron spectrum is most consistent with the semiclassical RR model.
5 Synchronization of focused femtosecond colliding PW laser pulses
In order to successfully collide PW femtosecond laser pulses, one needs to ensure the synchronization of the two focused pulses to better than the pulse duration. This is, for example, 45 fs for experiments with the colliding pulses in Astra Gemini PW Laser Facility (Section 4) and
![]() ${\sim}20~\text{fs}$
for the future experiments with colliding pulses with the ELI-NP
${\sim}20~\text{fs}$
for the future experiments with colliding pulses with the ELI-NP
![]() $2\times 10~\text{PW}$
Laser Facility under construction (Section 3). Both laser systems have one laser oscillator seeding the two laser amplifier chains with part of the laser pulse split from the same oscillator pulse. This laser system design ensures a natural synchronization between the two PW pulses emerging at the end of the two laser amplifier chains. The optical path traversed by the laser pulse in the two amplifier chains is nearly identical. The laser optical components are identical, the room temperature and humidity are kept constant and vibrations are minimized as much as possible. Nevertheless, there will be some small variations between the two optical paths, due to temperature variations, leading to temporal delay on the femtosecond timescale. Therefore additional, micrometre-size optimization of the path length of the two focused PW laser pulses needs to be implemented.
$2\times 10~\text{PW}$
Laser Facility under construction (Section 3). Both laser systems have one laser oscillator seeding the two laser amplifier chains with part of the laser pulse split from the same oscillator pulse. This laser system design ensures a natural synchronization between the two PW pulses emerging at the end of the two laser amplifier chains. The optical path traversed by the laser pulse in the two amplifier chains is nearly identical. The laser optical components are identical, the room temperature and humidity are kept constant and vibrations are minimized as much as possible. Nevertheless, there will be some small variations between the two optical paths, due to temperature variations, leading to temporal delay on the femtosecond timescale. Therefore additional, micrometre-size optimization of the path length of the two focused PW laser pulses needs to be implemented.
Experimentally, the femtosecond-level synchronization of the focused femtosecond pulses is measured and optimized in situ, in the focal spot of the two colliding pulses[Reference Corvan, Dzelzainis, Hyland, Nersisyan, Yeung, Zepf and Sarri25]. In order to perform the measurement, the energy of the colliding pulses is attenuated. A glass pellicle or a prism is inserted at the position of the two overlapping focal spots of the colliding pulses: the interaction point. Interference fringes are observed when the two laser pulses are synchronized[Reference Poder, Tamburini, Sarri, Di Piazza, Kuschel, Baird, Behm, Bohlen, Cole, Corvan, Duff, Gerstmayr, Keitel, Krushelnick, Mangles, McKenna, Murphy, Najmudin, Ridgers, Samarin, Symes, Thomas, Warwick and Zepf9, Reference Corvan, Dzelzainis, Hyland, Nersisyan, Yeung, Zepf and Sarri25]. In the experiments described in Section 4, the two colliding pulses, each with a 45 fs pulse duration, were overlapped[Reference Strickland and Mourou7, Reference Liu, Yu, Yin, Zhu and Shao13] to a precision of
![]() $\pm 30~\text{fs}$
.
$\pm 30~\text{fs}$
.
6 SHINE Facility: 100 PW pulse and 10 keV XFEL pulse for QED experiments
A further scaling in laser-pulse power from 10 PW to 100 PW and in laser intensity from
![]() ${>}10^{22}~\text{W}/\text{cm}^{2}$
to
${>}10^{22}~\text{W}/\text{cm}^{2}$
to
![]() ${>}10^{23}~\text{W}/\text{cm}^{2}$
is planned for the new SEL[Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6] facility being built at the SHINE Facility in Shanghai, China. This new facility is dedicated to exploring vacuum birefringence based on a 100 PW laser pulse and an X-ray free electron laser pulse[Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6]. SHINE will consist of a hard XFEL and the 100 PW laser. The 100 PW, femtosecond, laser pulse will be focused to an intensity of
${>}10^{23}~\text{W}/\text{cm}^{2}$
is planned for the new SEL[Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6] facility being built at the SHINE Facility in Shanghai, China. This new facility is dedicated to exploring vacuum birefringence based on a 100 PW laser pulse and an X-ray free electron laser pulse[Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6]. SHINE will consist of a hard XFEL and the 100 PW laser. The 100 PW, femtosecond, laser pulse will be focused to an intensity of
![]() $10^{23}~\text{W}/\text{cm}^{2}$
in vacuum. The 12.9 keV, femtosecond, X-ray pulse (from the XFEL) will traverse the focal volume irradiated by the laser. The linear polarization of the X-ray pulse will gain ellipticity due to vacuum birefringence occurring in the ultra-intense field of the focused laser.
$10^{23}~\text{W}/\text{cm}^{2}$
in vacuum. The 12.9 keV, femtosecond, X-ray pulse (from the XFEL) will traverse the focal volume irradiated by the laser. The linear polarization of the X-ray pulse will gain ellipticity due to vacuum birefringence occurring in the ultra-intense field of the focused laser.
A second, synchronized, 1 PW laser pulse will be available at the SEL facility. One can envisage QED experiments with two colliding 100 PW and 1 PW laser pulses. The 1 PW laser pulse will accelerate the electron bunch to ultra-relativistic energies. The ultra-relativistic electrons accelerated by the ‘first 1 PW pulse’ will travel through the focus of the ‘second 100 PW pulse’ where they are immersed in this ultra-intense,
![]() $I>10^{23}~\text{W}/\text{cm}^{2}$
, electromagnetic field and will generate the QED effects which will result in Gamma photons and electron–positron pair production. In this configuration, the X-ray pulse from the XFEL could be used as a probe pulse to look at Thomson scattering for example.
$I>10^{23}~\text{W}/\text{cm}^{2}$
, electromagnetic field and will generate the QED effects which will result in Gamma photons and electron–positron pair production. In this configuration, the X-ray pulse from the XFEL could be used as a probe pulse to look at Thomson scattering for example.
Another intriguing experiment would be to accelerate the electron bunch (LWFA) with the 100 PW pulse focused with an F/1000, extremely long effective focal length system:
![]() $f=1000~\text{m}$
. This could be achieved either by installing a 1000 m focal length mirror in the tunnel connecting SEL to the XFEL, or by focusing the laser beam with a telescope constructed of plasma mirrors (DN private communication). The plasma mirrors within the telescope would need replacing after each laser pulse. Such a geometry could investigate the acceleration of the electron bunch to multi-100 GeV energies in a single acceleration stage. The presently accepted scheme[Reference Leemans and Esarey26] envisages a chain of electron accelerators with each accelerator adding 10 GeV to the electron energy. Colliding ultra-high energy leptons (electron and positrons) instead of protons would be an important tool for the high energy physics research. The protons are not fundamental particles: they contain three constituent quarks, each of which participates in a collision. The electrons are fundamental particles. Therefore there are less degrees of freedom in the lepton compared to hadron collisions. For example a lepton–lepton collision only requires one impact parameter to be considered. The collision of two protons requires each quark impact parameter with every other quark in the other proton. There are more particles to be uncertain about the
$f=1000~\text{m}$
. This could be achieved either by installing a 1000 m focal length mirror in the tunnel connecting SEL to the XFEL, or by focusing the laser beam with a telescope constructed of plasma mirrors (DN private communication). The plasma mirrors within the telescope would need replacing after each laser pulse. Such a geometry could investigate the acceleration of the electron bunch to multi-100 GeV energies in a single acceleration stage. The presently accepted scheme[Reference Leemans and Esarey26] envisages a chain of electron accelerators with each accelerator adding 10 GeV to the electron energy. Colliding ultra-high energy leptons (electron and positrons) instead of protons would be an important tool for the high energy physics research. The protons are not fundamental particles: they contain three constituent quarks, each of which participates in a collision. The electrons are fundamental particles. Therefore there are less degrees of freedom in the lepton compared to hadron collisions. For example a lepton–lepton collision only requires one impact parameter to be considered. The collision of two protons requires each quark impact parameter with every other quark in the other proton. There are more particles to be uncertain about the
![]() $p$
–
$p$
–
![]() $p$
collisions compared to
$p$
collisions compared to
![]() $e$
–
$e$
–
![]() $e$
collisions.
$e$
collisions.
7 Simulation of copious electron–positron pair production with 2
 $\times$
10 PW colliding pulses
$\times$
10 PW colliding pulses
Simulations of colliding 10 PW laser pulses focused to ultra-high intensities predict large production of electron–positron pairs and very high laser energy conversion efficiency to hard Gamma photons [Reference Zhu, Yu, Sheng, Yin, Turcu and Pukhov11–Reference Luo, Wu, Liu, Ma, Li, Yuan, Yu, Chen and Sheng20].
In an interaction scheme simulation using laser parameters similar to the ELI-NP design capability, two counter-propagating ultra-intense laser pulses (
![]() $I\approx 3\times 10^{22}~\text{W}/\text{cm}^{2}$
, 40 fs pulse duration) are focused from two opposite directions on the near-critical-density plasmas filled inside two cone targets[Reference Zhu, Yu, Sheng, Yin, Turcu and Pukhov11]. This is shown schematically in Figure 7. The axes of the two cones are aligned to the laser propagation axis and each laser pulse is focused onto the base of its respective cone. The electrons immersed in the ultra-intense laser fields experience large RR forces by emitting photons so that a large number of electrons are trapped in the laser fields. These trapped electrons perform extreme oscillations in the transverse direction and emit intense Gamma-photon pulse around the laser axis. Copious numbers of electron–positron pairs are created via the multiphoton Breit–Wheeler process. The maximum accelerated electron energy is
$I\approx 3\times 10^{22}~\text{W}/\text{cm}^{2}$
, 40 fs pulse duration) are focused from two opposite directions on the near-critical-density plasmas filled inside two cone targets[Reference Zhu, Yu, Sheng, Yin, Turcu and Pukhov11]. This is shown schematically in Figure 7. The axes of the two cones are aligned to the laser propagation axis and each laser pulse is focused onto the base of its respective cone. The electrons immersed in the ultra-intense laser fields experience large RR forces by emitting photons so that a large number of electrons are trapped in the laser fields. These trapped electrons perform extreme oscillations in the transverse direction and emit intense Gamma-photon pulse around the laser axis. Copious numbers of electron–positron pairs are created via the multiphoton Breit–Wheeler process. The maximum accelerated electron energy is
![]() ${\sim}10~\text{GeV}/\text{electron}$
; maximum positron energy is
${\sim}10~\text{GeV}/\text{electron}$
; maximum positron energy is
![]() ${\sim}1.6~\text{GeV}/\text{positron}$
with maximum positron density of
${\sim}1.6~\text{GeV}/\text{positron}$
with maximum positron density of
![]() $4\times 10^{22}~\text{cm}^{-3}$
and a total positron yield of
$4\times 10^{22}~\text{cm}^{-3}$
and a total positron yield of
![]() ${\sim}10^{11}$
positrons/pulse; maximum Gamma-photon energy is
${\sim}10^{11}$
positrons/pulse; maximum Gamma-photon energy is
![]() ${\sim}5~\text{GeV}/\text{photon}$
. The laser energy conversion efficiency is very high:
${\sim}5~\text{GeV}/\text{photon}$
. The laser energy conversion efficiency is very high:
![]() ${\sim}9\%$
into electron bunch; 14.9% into Gamma-photon pulse; and 0.14% into positron bunch. The positron bunch produced by one plasma will collide with the accelerated electron bunch from the second plasma generating a microscopic multi-GeV electron–positron collider.
${\sim}9\%$
into electron bunch; 14.9% into Gamma-photon pulse; and 0.14% into positron bunch. The positron bunch produced by one plasma will collide with the accelerated electron bunch from the second plasma generating a microscopic multi-GeV electron–positron collider.
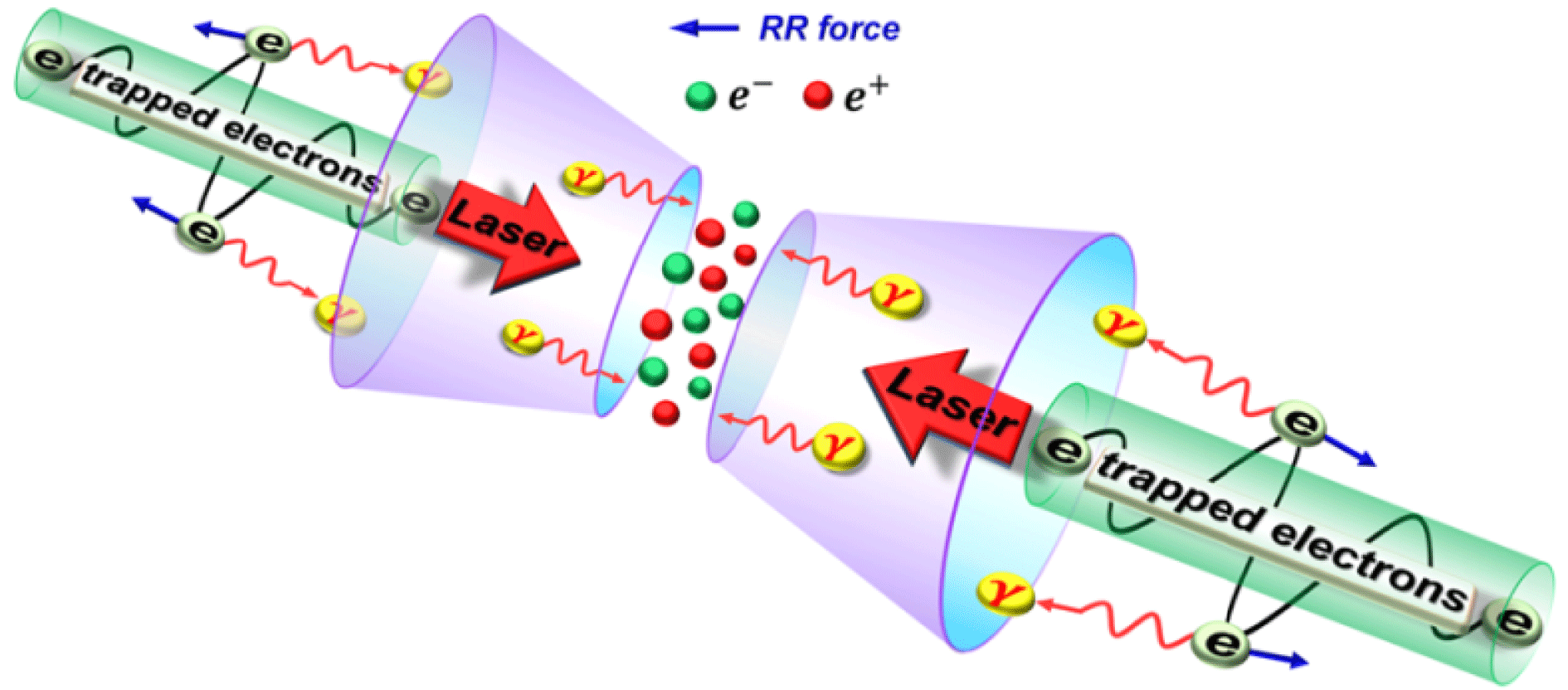
Figure 7. Bright Gamma-photon emission and copious electron–positron pair production from double-cone target filled with near-critical-density plasmas. (Courtesy X-L. Zhu and T-P. Yu.)
A second scheme[Reference Li, Yu, Liu, Yin, Zhu, Capdessus, Pegoraro, Sheng, McKenna and Shao12] simulates two colliding elliptically polarized 10 PW laser pulses incident onto two diamond-like carbon foils simultaneously, from both sides of the simulation box. The electrons in the focal region of one foil are rapidly accelerated by the laser radiation pressure and interact with the other intense laser pulse which penetrates through the second foil due to relativistically induced foil transparency. This symmetric configuration enables efficient Compton back-scattering and results in ultra-bright Gamma photon emission with brightness of
![]() ${\sim}10^{25}~\text{photons}/(\text{s}\,\cdot \,\text{mm}^{2}\,\cdot \,\text{mrad}^{2})$
for 0.1% BW at 15 MeV and intensity of
${\sim}10^{25}~\text{photons}/(\text{s}\,\cdot \,\text{mm}^{2}\,\cdot \,\text{mrad}^{2})$
for 0.1% BW at 15 MeV and intensity of
![]() $5\times 10^{23}~\text{W}/\text{cm}^{2}$
. Three-dimensional particle-in-cell simulations with QED incorporated show that a GeV positron beam with density of
$5\times 10^{23}~\text{W}/\text{cm}^{2}$
. Three-dimensional particle-in-cell simulations with QED incorporated show that a GeV positron beam with density of
![]() $2.5\times 10^{22}~\text{cm}^{-3}$
and flux of
$2.5\times 10^{22}~\text{cm}^{-3}$
and flux of
![]() $1.6\times 10^{10}$
per pulse is achieved. Collective effects of the electron–positron pair plasma may be also triggered, offering a new window on investigating laboratory astrophysics at PW laser facilities in the near future.
$1.6\times 10^{10}$
per pulse is achieved. Collective effects of the electron–positron pair plasma may be also triggered, offering a new window on investigating laboratory astrophysics at PW laser facilities in the near future.
A third scheme[Reference Liu, Yu, Yin, Zhu and Shao13–Reference Zhu, Zhu, Chen, Yu, Weng, Hu, McKenna and Sheng15] simulates the second colliding PW-class laser pulse being replaced by the reflection of the first pulse plasma mirror. The first laser pulse travelling through the plasma is reflected by the mirror and interacts with the high energy electron bunch generating copious Gamma photons and positrons. This new scheme would provide built-in femtosecond synchronization between the colliding pulses.
A fourth scheme[Reference Luo, Zhu, Zhuo, Ma, Song, Zhu, Wang, Li, Turcu and Chen16] simulates two colliding linearly polarized, 12.5 PW laser pulses irradiating a thin aluminium foil from both sides. Both lasers are focused to an intensity of
![]() $I=4\times 10^{23}~\text{W}/\text{cm}^{2}$
. About 20% of the laser energy is predicted to convert into a burst of Gamma photons with a flux exceeding
$I=4\times 10^{23}~\text{W}/\text{cm}^{2}$
. About 20% of the laser energy is predicted to convert into a burst of Gamma photons with a flux exceeding
![]() $10^{14}~\text{s}^{-1}$
. The conversion efficiency to Gamma photons in the case of two-side irradiation would be three times higher than that in the case of one-side irradiation with a single laser pulse. The predicted electron–positron plasma generated with colliding laser pulses would have a maximum density of
$10^{14}~\text{s}^{-1}$
. The conversion efficiency to Gamma photons in the case of two-side irradiation would be three times higher than that in the case of one-side irradiation with a single laser pulse. The predicted electron–positron plasma generated with colliding laser pulses would have a maximum density of
![]() $6\times 10^{27}~\text{m}^{-3}$
which would be eight-fold denser compared to the irradiation with only one laser pulse. Target transparency regime could further enhance the pair generations due to the predicted formation of a stable standing wave[Reference Liu, Luo, Yuan, Yu, Chen and Sheng17]. A scaling law of QED cascade growth with laser intensity is found[Reference Luo, Liu, Yuan, Chen, Yu, Li, Del Sorbo, Ridgers and Sheng18], which predicts that QED cascade saturation occurs for colliding laser intensities just exceeding
$6\times 10^{27}~\text{m}^{-3}$
which would be eight-fold denser compared to the irradiation with only one laser pulse. Target transparency regime could further enhance the pair generations due to the predicted formation of a stable standing wave[Reference Liu, Luo, Yuan, Yu, Chen and Sheng17]. A scaling law of QED cascade growth with laser intensity is found[Reference Luo, Liu, Yuan, Chen, Yu, Li, Del Sorbo, Ridgers and Sheng18], which predicts that QED cascade saturation occurs for colliding laser intensities just exceeding
![]() $10^{24}~\text{W}/\text{cm}^{2}$
. A high conversion efficiency of 10% from laser photons to electron–positron pairs is predicted in this regime. A high-yield (
$10^{24}~\text{W}/\text{cm}^{2}$
. A high conversion efficiency of 10% from laser photons to electron–positron pairs is predicted in this regime. A high-yield (
![]() ${\geqslant}10^{13}$
) ultradense
${\geqslant}10^{13}$
) ultradense
![]() $(10^{24}~\text{cm}^{-3})$
positron bunch is predicted which would constitute a new high field phenomenon: ‘QED pair plasma compression’. Consequent relativistic electron–positron jet formation along the transverse direction and high harmonic generation[Reference Yu, Yuan, Liu, Chen, Luo, Weng and Sheng19] along the longitudinal direction are predicted as the plasma squeezing effects become significant. The predicted laser-driven relativistic jets formation could be used to study energetic astrophysical phenomena in laboratory.
$(10^{24}~\text{cm}^{-3})$
positron bunch is predicted which would constitute a new high field phenomenon: ‘QED pair plasma compression’. Consequent relativistic electron–positron jet formation along the transverse direction and high harmonic generation[Reference Yu, Yuan, Liu, Chen, Luo, Weng and Sheng19] along the longitudinal direction are predicted as the plasma squeezing effects become significant. The predicted laser-driven relativistic jets formation could be used to study energetic astrophysical phenomena in laboratory.
A fifth simulation scheme[Reference Luo, Wu, Liu, Ma, Li, Yuan, Yu, Chen and Sheng20] employs two 10 PW-scale colliding lasers obliquely incident on a solid target. A high-yield
![]() $(3\times 10^{10})$
, overdense
$(3\times 10^{10})$
, overdense
![]() $({\sim}10^{22}~\text{cm}^{-3})$
positron bunch is predicted. Such positron yield is fifty times higher than that produced from a single laser with the same peak power.
$({\sim}10^{22}~\text{cm}^{-3})$
positron bunch is predicted. Such positron yield is fifty times higher than that produced from a single laser with the same peak power.
8 Conclusions
At the Schwinger laser intensity of
![]() $I_{S}=2.3\times 10^{29}~\text{W}/\text{cm}^{2}$
the QED theory predicts that a large part of the energy of the laser photons will be transformed to hard Gamma photons and even to matter: electron–positron pairs. The new laser facilities under construction, will use the interaction of two colliding PW laser pulses to reach the QED regime in experiments with the focused laser intensities which will become available in the near term:
$I_{S}=2.3\times 10^{29}~\text{W}/\text{cm}^{2}$
the QED theory predicts that a large part of the energy of the laser photons will be transformed to hard Gamma photons and even to matter: electron–positron pairs. The new laser facilities under construction, will use the interaction of two colliding PW laser pulses to reach the QED regime in experiments with the focused laser intensities which will become available in the near term:
![]() $I=10^{22}{-}10^{23}~\text{W}/\text{cm}^{2}$
and above. The first PW laser pulse will accelerate an electron bunch to relativistic energies of several GeV/electron, using either gas or solid targets; and the second PW laser pulse will be focused to the maximum intensity on the relativistic electron bunch in order to generate the QED effects. In this interaction geometry the relativistic electron experiences a much larger electric field, approaching the Schwinger field, in his own frame of reference than the actual laser electric field in the laboratory frame of reference.
$I=10^{22}{-}10^{23}~\text{W}/\text{cm}^{2}$
and above. The first PW laser pulse will accelerate an electron bunch to relativistic energies of several GeV/electron, using either gas or solid targets; and the second PW laser pulse will be focused to the maximum intensity on the relativistic electron bunch in order to generate the QED effects. In this interaction geometry the relativistic electron experiences a much larger electric field, approaching the Schwinger field, in his own frame of reference than the actual laser electric field in the laboratory frame of reference.
The new ELI-NP Laser Facility[Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3–Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Ataman, Cernaianu, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Matei, Seto, D’Alessi, Zeng and Zamfir5] in Romania will have an interaction chamber dedicated to QED experiments with two colliding 10 PW laser pulses focused to
![]() $I>10^{22}~\text{W}/\text{cm}^{2}$
. The SHINE Facility[Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6] in China will have a 100 PW laser pulse focused to
$I>10^{22}~\text{W}/\text{cm}^{2}$
. The SHINE Facility[Reference Shen, Bu, Xu, Xu, Ji, Li and Xu6] in China will have a 100 PW laser pulse focused to
![]() $I>10^{23}~\text{W}/\text{cm}^{2}$
. This pulse can be collided with a second PW focused laser pulse. Experiments with two colliding 0.25 PW laser pulses were conducted at the Astra Gemini PW Laser Facility[Reference Hooker, Collier, Chekhlov, Clarke, Divall, Ertel, Fell, Foster, Hancock, Langley, Neely and Smith10] in the UK by the collaboration led by the Queen’s University Belfast and Imperial College London[Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8, Reference Poder, Tamburini, Sarri, Di Piazza, Kuschel, Baird, Behm, Bohlen, Cole, Corvan, Duff, Gerstmayr, Keitel, Krushelnick, Mangles, McKenna, Murphy, Najmudin, Ridgers, Samarin, Symes, Thomas, Warwick and Zepf9]. Clear evidence of RR was measured from the energy spectrum of the emitted Gamma photons and from the energy loss by electrons recoiling from the emission of Gamma photons. The two colliding pulses, each with a 45 fs pulse duration, were overlapped to a precision of
$I>10^{23}~\text{W}/\text{cm}^{2}$
. This pulse can be collided with a second PW focused laser pulse. Experiments with two colliding 0.25 PW laser pulses were conducted at the Astra Gemini PW Laser Facility[Reference Hooker, Collier, Chekhlov, Clarke, Divall, Ertel, Fell, Foster, Hancock, Langley, Neely and Smith10] in the UK by the collaboration led by the Queen’s University Belfast and Imperial College London[Reference Cole, Behm, Gerstmayr, Blackburn, Wood, Baird, Duff, Harvey, Ilderton, Joglekar, Krushelnick, Kuschel, Marklund, McKenna, Murphy, Poder, Ridgers, Samarin, Sarri, Symes, Thomas, Warwick, Zepf, Najmudin and Mangles8, Reference Poder, Tamburini, Sarri, Di Piazza, Kuschel, Baird, Behm, Bohlen, Cole, Corvan, Duff, Gerstmayr, Keitel, Krushelnick, Mangles, McKenna, Murphy, Najmudin, Ridgers, Samarin, Symes, Thomas, Warwick and Zepf9]. Clear evidence of RR was measured from the energy spectrum of the emitted Gamma photons and from the energy loss by electrons recoiling from the emission of Gamma photons. The two colliding pulses, each with a 45 fs pulse duration, were overlapped to a precision of
![]() $\pm 30~\text{fs}$
.
$\pm 30~\text{fs}$
.
Theoretical simulations[Reference Zhu, Yu, Sheng, Yin, Turcu and Pukhov11–Reference Luo, Wu, Liu, Ma, Li, Yuan, Yu, Chen and Sheng20] guide the experiments and predict copious electron–positron and Gamma-photon generation from the collision of two focused pulses with intensities ranging from
![]() $I=10^{22}~\text{W}/\text{cm}^{2}$
to
$I=10^{22}~\text{W}/\text{cm}^{2}$
to
![]() $10^{23}~\text{W}/\text{cm}^{2}$
and to
$10^{23}~\text{W}/\text{cm}^{2}$
and to
![]() $10^{24}~\text{W}/\text{cm}^{2}$
. The targets used in simulations are solid thin foils or cones filled with near-critical plasmas. Simulations predict generation of positron bunches reaching densities
$10^{24}~\text{W}/\text{cm}^{2}$
. The targets used in simulations are solid thin foils or cones filled with near-critical plasmas. Simulations predict generation of positron bunches reaching densities
![]() ${>}10^{22}~\text{cm}^{-3}$
and energies of
${>}10^{22}~\text{cm}^{-3}$
and energies of
![]() ${>}\text{GeV}/\text{positron}$
. Laser photons to Gamma photons conversion efficiencies
${>}\text{GeV}/\text{positron}$
. Laser photons to Gamma photons conversion efficiencies
![]() ${>}$
10% are predicted. Orders of magnitude enhancement of pair production is predicted when using colliding laser pulses as compared to one-side laser irradiation of targets.
${>}$
10% are predicted. Orders of magnitude enhancement of pair production is predicted when using colliding laser pulses as compared to one-side laser irradiation of targets.
Acknowledgements
ICET acknowledges the collaboration of the co-authors to this paper and in Refs. [Reference Turcu, Negoita, Jaroszynski, Mckenna, Balascuta, Ursescu, Dancus, Cernaianu, Tataru, Ghenuche, Stutman, Boianu, Risca, Toma, Petcu, Acbas, Yoffe, Noble, Ersfeld, Brunetti, Capdessus, Murphy, Ridgers, Neely, Mangles, Gray, Thomas, Kirk, Ilderton, Marklund, Gordon, Hafizi, Kaganovich, Palastro, D’humieres, Zepf, Sarri, Gies, Karbstein, Schreiber, Paulus, Dromey, Harvey, Di Piazza, Keitel, Kaluza, Gales and Zamfir3, Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Balascuta, Cappuzzello, Cernaianu, Chen, Dancus, Freeman, Geissel, Genuche, Gizzi, Gobet, Gosselin, Gugiu, Higginson, D’humières, Ivan, Jaroszynski, Kar, Lamia, Leca, Neagu, Lanzalone, Méot, Mirfayzi, Mitu, Morel, Murphy, Petcu, Petrascu, Petrone, Raczka, Risca, Rotaru, Santos, Schumacher, Stutman, Tarisien, Tataru, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir4] in bringing into focus on the concept of QED experiments with colliding PW laser pulses: experimental (several laboratories and scientists) and theoretical simulations (several groups and scientists).
ICET: support from the National Key Research and Development Program of China (No. 2016YFA0300803). BS: support from the Project of Shanghai HIgh repetition rate XFEL aNd Extreme light facility (SHINE) and the Strategic Priority Research Program of Chinese Academy of Sciences (No. XDB16). GS: support from the EPSRC, UK (Nos. EP/L013975 and EP/N022696/1) and technical support from the Central Laser Facility (CLF). KAT and ICET: support from Extreme Light Infrastructure Nuclear Physics (ELI-NP) Phase II, a project co-financed by the Romanian Government and the European Union through the European Regional Development Fund. PMcK: support from EPSRC (No. EP/M018091/1). SPDM acknowledges the support from EPSRC (No. EP/M018555/1), STFC (Nos. ST/J002062/1 and ST/P002021/1) and Horizon 2020 funding from the European Research Council (ERC) (No. 682399) and technical support from the CLF. TPY, ZXL and YY: support from the National Natural Science Foundation of China (Nos. 11622547, 11875319, 11875091, 11474360, and 11175255), the National Key Research and Development Program of China (No. 2018YFA0404802), the Science Challenge Program (No. TZ2016005), and the Hunan Province Science and Technology Program of China (No. 2017RS3042). WL: supported by the National Natural Science Foundation of China (Nos. 11347028, 11405083, and 11675075). The EPOCH code used in the research by TPY, ZXL, YY and WL was developed under UK Engineering and Physics Sciences Research Council (Nos. EP/G054940/1, EP/G055165/1, and EP/G056803/1).