1 Introduction
Strong-field terahertz sources have played important roles in nonlinear terahertz spectroscopy[ Reference Hwang, Fleischer, Brandt, Perkins, Liu, Fan, Sternbach, Zhang, Averitt and Nelson 1 – Reference Kampfrath, Tanaka and Nelson 3 ], strong-field terahertz physics[ Reference Kampfrath, Sell, Klatt, Pashkin, Mährlein, Dekorsy, Wolf, Fiebig, Leitenstorfer and Huber 4 , Reference Schubert, Hohenleutner, Langer, Urbanek, Lange, Huttner, Golde, Meier, Kira, Koch and Huber 5 ], electron manipulation[ Reference Takeda, Yoshioka, Minami and Katayama 6 ], particle acceleration[ Reference Liu, Sun, Yu, Liu, Jia, Sun and Xu 7 ], etc. There are a few available technologies that permit powerful terahertz generation, such as the free electron laser (FEL)[ Reference Daranciang, Goodfellow, Fuchs, Wen, Ghimire, Reis, Loos, Fisher and Lindenberg 8 , Reference Li, Lu, He, Jia and Wang 9 ], photoconductive antenna (PCA)[ Reference Kasai, Watanabe and Ouchi 10 – Reference Ropagnol, Khorasaninejad, Raeiszadeh, Safavi-Naeini, Bouvier, Côté, Laramée, Reid, Gauthier and Ozaki 13 ], spintronic terahertz emitter (STE)[ Reference Seifert, Cheng, Wei, Kampfrath and Qi 14 , Reference Rouzegar, Chekhov, Behovits, Serrano, Syskaki, Lambert, Engel, Martens, Münzenberg, Wolf, Jakob, Kläui, Seifert and Kampfrath 15 ], laser–plasma interaction[ Reference Hamster, Sullivan, Gordon, White and Falcone 16 , Reference Koulouklidis, Gollner, Shumakova, Fedorov, Pugžlys, Baltuška and Tzortzakis 17 ] and optical rectification (OR)[ Reference Hauri, Ruchert, Vicario and Ardana 18 – Reference Polónyi, Monoszlai, Andriukaitis, Gäumann, Balciunas, Pugzlys, Baltuska, Feurer, Hebling and Fülöp 21 ]. The FEL can produce a strong terahertz field with peak amplitude up to dozens of MV/cm, but it is accompanied by the obvious shortcomings of huge volume, high complexity and unacceptable cost. The PCA suffers from a limited damage threshold so that the terahertz field is relatively low even if a large-aperture PCA is used[ Reference Ropagnol, Khorasaninejad, Raeiszadeh, Safavi-Naeini, Bouvier, Côté, Laramée, Reid, Gauthier and Ozaki 13 ]. The plasma excited by high-intensity femtosecond laser pulses emits ultra-broadband coherent radiation spanning from X-ray to terahertz waves and the terahertz field can be further enhanced by two-color filamentation[ Reference Hamster, Sullivan, Gordon, White and Falcone 16 , Reference Koulouklidis, Gollner, Shumakova, Fedorov, Pugžlys, Baltuška and Tzortzakis 17 ]. Due to its highly nonlinear and phase-sensitive nature in laser–gas interaction, the stability is a major problem[ Reference Zhang, Li and Zhao 22 ]. Based on spintronics in a ferromagnetic/non-magnetic heterostructure, the STE is promising for terahertz generation with a wide frequency band, low cost and high field intensity[ Reference Rouzegar, Chekhov, Behovits, Serrano, Syskaki, Lambert, Engel, Martens, Münzenberg, Wolf, Jakob, Kläui, Seifert and Kampfrath 15 ]. It has attracted much attention in recent years and its significance in ultra-broadband measurements, magnetic structure imaging and near-field microscopy has been recognized. However, there is an obstacle for STE to produce multi-cycle terahertz pulses and the technological maturity is still a problem for applications at the present stage. Generally, OR, which originates from second-order nonlinear optical (NLO) effects induced by ultrashort laser pulses, is believed to be the most effective and practical technology to obtain table-top terahertz sources with high efficiency close to or even beyond the Manley–Rowe limit. The major concerns of OR include the physical and optical properties of the NLO crystal, as well as the feasibility of realizing the phase-matching (PM) condition.
Semiconductor crystals such as ZnTe and GaP have reasonable transmission in the terahertz range and PM can be fulfilled at a suitable pump wavelength, for example, ZnTe pumped by Ti:sapphire lasers around 800 nm and GaP pumped by Yb-doped lasers around 1030 nm[ Reference Blanchard, Razzari, Bandulet, Sharma, Morandotti, Kieffer, Ozaki, Reid, Tiedje, Haugen and Hegmann 23 – Reference Hekmat, Vogel, Wang, Mansourzadeh, Aslani, Omar, Hoffmann, Meyer and Saraceno 25 ]. A low laser-induced damage threshold (LIDT) and high two-photon absorption (2PA) due to the narrow bandgap are the primary defects of these semiconductors[ Reference Ji, Kukaswadia, Feng, Tang and Becla 26 , Reference Gonzalez, Guha and Trivedi 27 ], which severely limits the conversion efficiency and maximum terahertz pulse energy[ Reference Zhang, Li and Zhao 22 ]. Organic crystals possess extremely high nonlinearity and can produce strong terahertz pulses within one coherent length, represented by DAST and BNA[ Reference Hauri, Ruchert, Vicario and Ardana 18 , Reference Roeder, Shalaby, Beleites, Ronneberger and Gopal 19 ], but they are usually excluded by robust systems because of deliquescence, a low LIDT and serious terahertz absorption[ Reference Zhang, Li and Zhao 22 ]. As a popular crystalline material in nonlinear optics, lithium niobate (LiNbO3) has a wide bandgap and a high nonlinear coefficient and LIDT[ Reference Meng, Zhang, Zhong and Zhu 28 , Reference Moriguchi, Tokizane, Takida, Nawata, Eno, Nagano and Minamide 29 ], enabling widely tunable terahertz generation via stimulated polariton scattering[ Reference Moriguchi, Tokizane, Takida, Nawata, Eno, Nagano and Minamide 29 – Reference Wang, Tang, Xu, Yan, He, Shi, Yan, Liu, Nie, Feng and Yao 31 ]. However, LiNbO3-based OR was unachievable for a long time due to the difficulty in PM[ Reference Zhang, Li and Zhao 22 ], until the tilted-pulse-front (TPF) technique was proposed.
The TPF technique was first introduced into OR in 2002[ Reference Hebling, Almási, Kozma and Kuhl 32 ]. Since then, TPF OR has been extensively studied, mainly focusing on LiNbO3 and some cubic semiconductors[ Reference Zhang, Ma, Ma, Wu, Ouyang, Kong, Hong, Wang, Yang, Chen, Li and Zhang 20 , Reference Polónyi, Monoszlai, Andriukaitis, Gäumann, Balciunas, Pugzlys, Baltuska, Feurer, Hebling and Fülöp 21 , Reference Fülöp, Pálfalvi, Klingebiel, Almási, Krausz, Karsch and Hebling 33 – Reference Blanchard, Schmidt, Ropagnol, Thiré, Ozaki, Morandotti, Cooke and Légaré 50 ]. The special significance of the TPF is that it greatly lowers the rigorous requirement for PM condition in OR. The TPF allows for pumping at a longer wavelength to reduce free-carrier absorption (FCA), which is mainly caused by 2PA and can improve the OR efficiency in cubic semiconductors such as ZnTe and GaAs[ Reference Polónyi, Monoszlai, Andriukaitis, Gäumann, Balciunas, Pugzlys, Baltuska, Feurer, Hebling and Fülöp 21 , Reference Ollmann, Fülöp, Hebling and Almási 49 , Reference Blanchard, Schmidt, Ropagnol, Thiré, Ozaki, Morandotti, Cooke and Légaré 50 ]. Moreover, PM for LiNbO3 OR pumped by intense femtosecond lasers can be realized for efficient strong-field terahertz generation at a typical TPF angle around 63°[ Reference Zhang, Ma, Ma, Wu, Ouyang, Kong, Hong, Wang, Yang, Chen, Li and Zhang 20 , Reference Fülöp, Pálfalvi, Klingebiel, Almási, Krausz, Karsch and Hebling 33 – Reference Lombosi, Polónyi, Mechler, Ollmann, Hebling and Fülöp 37 ]. Quite a few theoretical models have been developed to explain and optimize this technique[ Reference Fülöp, Pálfalvi, Almási and Hebling 38 – Reference Wang, Tóth, Hebling and Kärtner 48 ]. The maximum single-pulse energy has reached the milestone mJ level recently[ Reference Zhang, Ma, Ma, Wu, Ouyang, Kong, Hong, Wang, Yang, Chen, Li and Zhang 20 ], which is of great significance to motivate extreme terahertz applications. However, only the low-frequency region below 3.5 THz can be generated via TPF OR in LiNbO3. Limited by the sharp increase of the absorption coefficient due to phonon vibrations[ Reference Pálfalvi, Hebling, Kuhl, Péter and Polgár 51 , Reference Wu, Zhou, Huang, Ahr and Kärtner 52 ], extending the terahertz spectrum to the high-frequency part in LiNbO3 is extremely difficult. In addition, the large TPF angle in LiNbO3 causes serious beam distortion[ Reference Polónyi, Monoszlai, Andriukaitis, Gäumann, Balciunas, Pugzlys, Baltuska, Feurer, Hebling and Fülöp 21 , Reference Lombosi, Polónyi, Mechler, Ollmann, Hebling and Fülöp 37 , Reference Fülöp, Pálfalvi, Almási and Hebling 38 , Reference Ollmann, Fülöp, Hebling and Almási 49 ] and group velocity dispersion due to angular dispersion (GVD-AD)[ Reference Ravi, Huang, Carbajo, Wu and Kärtner 43 , Reference Ravi, Huang, Carbajo, Nanni, Schimpf, Ippen and Kärtner 44 ], which prevents maintaining the PM condition in the cascaded difference frequency generation (DFG) process.
Filling up the nonexistent high-frequency terahertz spectrum has always been desired but impossible by TPF OR in LiNbO3, until we focused on crystalline silicon carbide (SiC), a representative wide-bandgap semiconductor material. SiC has more than 200 polymorphs, among which the positive uniaxial 4H-SiC crystal (6mm group point) is the most promising in nonlinear optics. 4H-SiC has an ultra-high LIDT (up to 80 GW/cm2 with a 10 ns laser pulse at 1064 nm[ Reference Niedermeier, Schillinger, Sauerbrey, Adolph and Bechstedt 53 ]), wideband transparency (0.37–5.6 μm and 0.1–18 THz[ Reference Nakayama, Matsubara, Okajima, Kawahata, Tanaka, Akiyama, Kinoshita, Yoshimoto and Takahashi 54 – Reference Fischer, Bühler, Fitzky, Kurihara, Eggert, Leitenstorfer and Brida 58 ]) and a large bandgap (3.26 eV[ Reference Harris 59 ]) compared with all other available second-order nonlinear crystals for terahertz generation. Its excellent optical properties guarantee intense optical pumping under powerful Ti:sapphire amplifiers[ Reference Fischer, Bühler, Fitzky, Kurihara, Eggert, Leitenstorfer and Brida 58 ] to generate strong-field and broadband terahertz radiation. There have been a few reports exploring the potential of SiC crystals in terahertz generation via NLO effects in recent years. Strait et al. [ Reference Strait, George, Dawlaty, Shivaraman, Chandrashekhar, Rana and Spencer 60 ] demonstrated coherent terahertz radiation produced by OR in a 6H-SiC wafer for the first time. Naftaly et al. [ Reference Naftaly, Molloy, Magnusson, Andreev and Lanskii 57 ] measured the transparency and birefringence of 4H-SiC in the range of 0.1–20 THz, and predicted broadband terahertz generation up to 18 THz by DFG. Fischer et al. [ Reference Fischer, Bühler, Fitzky, Kurihara, Eggert, Leitenstorfer and Brida 58 ] achieved a tunable transient DFG terahertz source between 5 and 15 THz using 4H-SiC pumped by two femtosecond lasers, and electro-optic detection based on 4H-SiC as well. However, simultaneous generation of a broadband terahertz spectrum in 4H-SiC covering the transparent range has been impossible due to the challenge in fulfilling the PM condition. In addition, the high LIDT of this material has not been fully used, which greatly limits the conversion efficiency. Once an extremely strong pump field is applied, an essential condition to ensure high OR efficiency in 4H-SiC, the self-phase modulation (SPM) and FCA effects would become critical in the nonlinear process.
Considering the bright prospect of 4H-SiC in strong-field broadband terahertz generation by OR, the TPF technique is introduced under intense laser pumping in this paper. Compared with LiNbO3, the TPF angle required for 4H-SiC is much smaller, which reduces the GVD-AD and beam distortion, increases the effective interaction length and uniformity in terahertz generation and favors 1D spatial model analysis to simulate the dynamics based on the fourth-order Runge–Kutta method. The accuracy of the model was assured by simultaneous consideration of the following factors: (i) the NLO coupled interaction of the terahertz and optical waves, reflected in the resonant cascading effects, including cascaded DFG and sum frequency generation (SFG); (ii) angular dispersion (AD) and material dispersion (MD); (iii) linear absorption and FCA at the terahertz frequency caused by three-photon absorption (3PA); (iv) SPM; (v) pre-chirping of the input pump pulses. On this basis, the evolution of terahertz and optical waves was analyzed quantitatively. Ultimately, ultra-widely tunable (up to over 14 THz), high-efficiency (~10–2) and strong-field (MV/cm) terahertz generation was predicted by illuminating well-chirped ultrashort (30 fs) laser pulses at 800 nm to 4H-SiC crystals. It was shown that single- and multi-cycle terahertz pulses can be modulated by pre-chirping and the central frequency of the terahertz spectrum is tunable by varying the TPF angle. The results indicate that 4H-SiC enables the terahertz frequency extending to an unprecedent range by OR, which has extremely important potential in strong-field terahertz applications.
2 Theoretical model
Matching between the group velocity of ultrashort optical pulses and the phase velocity of terahertz waves determines the OR efficiency, where the main influence factors include the pump wavelength, polarization and crystal orientation. The TPF gives another freedom, the TPF angle γ, to fulfill the matching condition with variable optical wavelength and terahertz frequency. The requirement of γ is calculated by cosγ = n g/n THz [ Reference Hebling, Almási, Kozma and Kuhl 32 ], where n g and n THz are the group refractive index of the optical pulse and phase refractive index of terahertz waves, respectively. Based on the Sellmeier equations of 4H-SiC[ Reference Wang, Zhan, Wang, Xuan, Zhang, Liu, Xu, Liu, Wei and Chen 55 , Reference Fischer, Bühler, Fitzky, Kurihara, Eggert, Leitenstorfer and Brida 58 ], the typical TPF angle of γ = 32° is obtained by substituting n g = 2.7610 (λ op = 800 nm) and n THz = 3.2445 (λ THz = 60 μm) for the e-e→e PM condition. Such a TPF angle is half that in LiNbO3, which highly benefits the TPF OR process. In addition to increasing the effective interaction length, improving spatial uniformity and alleviating distortion, a smaller TPF angle also promises better simulation accuracy. A variety of theoretical models have been developed so far[ Reference Fülöp, Pálfalvi, Almási and Hebling 38 – Reference Wang, Tóth, Hebling and Kärtner 48 ], basically including 1D to 3D spatial models with/without considering the cascading effects, among which the 1D model with cascading effects is believed to best fit the situation here. On one hand, the 1D model greatly simplifies the complexity while ensuring accuracy in the case of a small TPF angle. On the other hand, the spectral re-shaping of the optical pump pulse via cascading effects requires consideration, otherwise the conversion efficiency will be overestimated. Finally, when illuminated by strong laser pulses, complex nonlinear processes including SPM and the photon absorption-induced FCA of terahertz waves, cannot be neglected. The 1D coupled wave equations of TPF OR with cascading, SPM and FCA effects are given by the following[ Reference Wu, Chai, Ma, Zhang, Xia, Fang, Kong, Wang, Liu, Zhu, Wang, Ruan and Li 35 , Reference Fülöp, Pálfalvi, Hoffmann and Hebling 39 ]:
 $$\begin{align}\begin{array}{l}\frac{\mathrm{d}A_\mathrm{THz}\left(\Omega, z\right)}{\mathrm{d}z}=-\frac{\alpha_\mathrm{THz}\left(\Omega \right)}{2}{A}_\mathrm{THz}\left(\Omega, z\right)-\frac{j{\Omega}^2}{2{c}^2k\left(\Omega \right)}{\chi}_\mathrm{eff}^{(2)}\\ \cdot{}\underset{0}{\overset{\infty }{\int }}{A}_{\mathrm{op}}\left(\omega +\Omega, z\right){A}_\mathrm{op}^{\ast}\left(\omega, z\right)\exp \left\{-j\left[k\left(\omega +\Omega \right)-k\left(\omega \right)-k\left(\Omega \right)\right]z\right\} \mathrm{d}\omega, \end{array}\end{align}$$
$$\begin{align}\begin{array}{l}\frac{\mathrm{d}A_\mathrm{THz}\left(\Omega, z\right)}{\mathrm{d}z}=-\frac{\alpha_\mathrm{THz}\left(\Omega \right)}{2}{A}_\mathrm{THz}\left(\Omega, z\right)-\frac{j{\Omega}^2}{2{c}^2k\left(\Omega \right)}{\chi}_\mathrm{eff}^{(2)}\\ \cdot{}\underset{0}{\overset{\infty }{\int }}{A}_{\mathrm{op}}\left(\omega +\Omega, z\right){A}_\mathrm{op}^{\ast}\left(\omega, z\right)\exp \left\{-j\left[k\left(\omega +\Omega \right)-k\left(\omega \right)-k\left(\Omega \right)\right]z\right\} \mathrm{d}\omega, \end{array}\end{align}$$
 $$\begin{align}\begin{array}{l}\frac{\mathrm{d}A_\mathrm{op}\left(\omega, z\right)}{\mathrm{d}z}=-\frac{\alpha_\mathrm{op}\left(\Omega \right)}{2}{A}_\mathrm{op}\left(\omega, z\right)-\frac{j{\omega}^2}{2{c}^2k\left(\omega \right)}{\chi}_\mathrm{eff}^{(2)}\\ \cdot{}\left\{\underset{0}{\overset{\infty }{\int }}{A}_\mathrm{op}\left(\omega +\Omega, z\right){A}_\mathrm{THz}^{\ast}\left(\Omega, z\right)\exp \left\{-j\left[k\left(\omega +\Omega \right)-k\left(\omega \right)-k\left(\Omega \right)\right]z\right\}\right.\\ {}\left.+\underset{0}{\overset{\infty }{\int }}{A}_\mathrm{op}\left(\omega -\Omega, z\right){A}_\mathrm{THz}\left(\Omega, z\right)\exp \left\{-j\left[k\left(\omega -\Omega \right)-k\left(\omega \right)+k\left(\Omega \right)\right]z\right\}\right\}\mathrm{d}\Omega \\ {}- \mathrm{Ft}\left[j\frac{\varepsilon_0{\omega}_0n\left({\omega}_0\right){n}_2\left({z}\right)}{2}{\left|{A}_\mathrm{op}\left({z},{t}\right)\right|}^2{A}_\mathrm{op}\left({z},{t}\right)\right],\end{array}\end{align}$$
$$\begin{align}\begin{array}{l}\frac{\mathrm{d}A_\mathrm{op}\left(\omega, z\right)}{\mathrm{d}z}=-\frac{\alpha_\mathrm{op}\left(\Omega \right)}{2}{A}_\mathrm{op}\left(\omega, z\right)-\frac{j{\omega}^2}{2{c}^2k\left(\omega \right)}{\chi}_\mathrm{eff}^{(2)}\\ \cdot{}\left\{\underset{0}{\overset{\infty }{\int }}{A}_\mathrm{op}\left(\omega +\Omega, z\right){A}_\mathrm{THz}^{\ast}\left(\Omega, z\right)\exp \left\{-j\left[k\left(\omega +\Omega \right)-k\left(\omega \right)-k\left(\Omega \right)\right]z\right\}\right.\\ {}\left.+\underset{0}{\overset{\infty }{\int }}{A}_\mathrm{op}\left(\omega -\Omega, z\right){A}_\mathrm{THz}\left(\Omega, z\right)\exp \left\{-j\left[k\left(\omega -\Omega \right)-k\left(\omega \right)+k\left(\Omega \right)\right]z\right\}\right\}\mathrm{d}\Omega \\ {}- \mathrm{Ft}\left[j\frac{\varepsilon_0{\omega}_0n\left({\omega}_0\right){n}_2\left({z}\right)}{2}{\left|{A}_\mathrm{op}\left({z},{t}\right)\right|}^2{A}_\mathrm{op}\left({z},{t}\right)\right],\end{array}\end{align}$$
and the wave numbers of the terahertz and optical fields are as follows:
 $$\begin{align}k\left(\omega \right)=\frac{1}{\cos \gamma}\frac{n\left(\omega \right)\omega }{c}-\frac{{\left(\omega -{\omega}_0\right)}^2}{2}\frac{n_\mathrm{g}^2\left({\omega}_0\right)}{\omega_0 cn\left({\omega}_0\right)}\mathrm{ta}{\mathrm{n}}^2\gamma,\end{align}$$
$$\begin{align}k\left(\omega \right)=\frac{1}{\cos \gamma}\frac{n\left(\omega \right)\omega }{c}-\frac{{\left(\omega -{\omega}_0\right)}^2}{2}\frac{n_\mathrm{g}^2\left({\omega}_0\right)}{\omega_0 cn\left({\omega}_0\right)}\mathrm{ta}{\mathrm{n}}^2\gamma,\end{align}$$
respectively, where ω and Ω represent the angular frequencies of the optical and terahertz waves, respectively, A
op and A
THz are the envelopes of the optical and terahertz fields, respectively, α
op and α
THz are the absorptions in the optical and terahertz regions, respectively, c is the speed of light in the vacuum,
![]() ${\chi}_{\mathrm{eff}}^{(2)}$
is the effective second-order nonlinear susceptibility, ε
0 is the vacuum permittivity, ω
0 is the central optical angular frequency and n and n
2 are the refractive index and nonlinear refractive index[
Reference Wang, Zhan, Wang, Xuan, Zhang, Liu, Xu, Liu, Wei and Chen
55
,
Reference Fischer, Bühler, Fitzky, Kurihara, Eggert, Leitenstorfer and Brida
58
,
Reference Guo, Peng, Ding, Li, Chen, Wei, Tong and Guo
61
], respectively. Equation (1a) describes terahertz generation by DFG between different optical frequency components, while Equation (1b) indicates the DFG and SFG processes between optical and terahertz frequencies. The last term of the Equation (1b) shows the SPM effect, which would widen the optical spectrum significantly under intense pumping, resulting in a decrease of pump spectral intensities and hindering terahertz generation seriously. The spectral widening caused by stimulated Raman scattering (SRS) was ignored because the major Raman peak of 4H-SiC locates at around 23 THz, beyond the bandwidth of typical Ti:sapphire laser pulses with a Fourier-transform-limited (FTL) duration of 30 fs[
Reference Nagai, Matsubara and Ashida
62
]. The second term of the Equation (2b) corresponds to GVD due to AD, which deteriorates the PM condition with the red shifting pump spectrum.
${\chi}_{\mathrm{eff}}^{(2)}$
is the effective second-order nonlinear susceptibility, ε
0 is the vacuum permittivity, ω
0 is the central optical angular frequency and n and n
2 are the refractive index and nonlinear refractive index[
Reference Wang, Zhan, Wang, Xuan, Zhang, Liu, Xu, Liu, Wei and Chen
55
,
Reference Fischer, Bühler, Fitzky, Kurihara, Eggert, Leitenstorfer and Brida
58
,
Reference Guo, Peng, Ding, Li, Chen, Wei, Tong and Guo
61
], respectively. Equation (1a) describes terahertz generation by DFG between different optical frequency components, while Equation (1b) indicates the DFG and SFG processes between optical and terahertz frequencies. The last term of the Equation (1b) shows the SPM effect, which would widen the optical spectrum significantly under intense pumping, resulting in a decrease of pump spectral intensities and hindering terahertz generation seriously. The spectral widening caused by stimulated Raman scattering (SRS) was ignored because the major Raman peak of 4H-SiC locates at around 23 THz, beyond the bandwidth of typical Ti:sapphire laser pulses with a Fourier-transform-limited (FTL) duration of 30 fs[
Reference Nagai, Matsubara and Ashida
62
]. The second term of the Equation (2b) corresponds to GVD due to AD, which deteriorates the PM condition with the red shifting pump spectrum.
The SPM effect can be relieved effectively via pre-chirping before injecting the pump beam because of the reduction of pump intensity due to pulse broadening. Given that the Gaussian envelope of the electric field is A(t), its frequency-domain expression after chirping is as follows:
where ϕ(ω) is the frequency-dependent additional phase, given by the following:
where GDD and TOD are the group delay dispersion and third-order dispersion, respectively. Here, ϕ(ω) leads to the broadening of the pulse duration and further affects the PM condition, as shown in Equation (1).
Unlike the photogenerated carriers in the photo-Dember effect, which help screen the doping-induced interfacial electric field and generate terahertz radiation in the form of the time derivative of the net current[ Reference Apostolopoulos and Barnes 63 , Reference Wu, Guo, Tu, Lyu, Wang, Li, Zhou, Zhang, Zhao and Yuan 64 ], the photogenerated carriers in OR tend to exhibit the absorption of photons. Under intense pumping, the increase of free-carrier density caused by photon absorption leads to a serious FCA effect, and thus the absorption is increased to α THz + α fc instead of the original α THz in Equation (1) [ Reference Zhong, Zhai, Li, Zhu, Li, Meng, Liu, Du, Zhao and Li 65 ]. The density of the free carrier N fc is given by the following[ Reference Zhong, Zhai, Li, Zhu, Li, Meng, Liu, Du, Zhao and Li 65 ]:
 $$\begin{align}{N}_\mathrm{fc}=\frac{IT_{z}}{hc/{\lambda}_0}\left({\alpha}_1+\frac{1}{2}{\alpha}_2I+\frac{1}{3}{\alpha}_3{I}^2+\dots \right),\end{align}$$
$$\begin{align}{N}_\mathrm{fc}=\frac{IT_{z}}{hc/{\lambda}_0}\left({\alpha}_1+\frac{1}{2}{\alpha}_2I+\frac{1}{3}{\alpha}_3{I}^2+\dots \right),\end{align}$$
where I is the time-averaged pump pulse intensity over the pulse duration, λ 0 is the central pump wavelength and α 1, α 2 and α 3 are the linear, 2PA and 3PA coefficients, respectively. Only 3PA is considered because of the large band gap of 4H-SiC[ Reference Guo, Peng, Ding, Li, Chen, Wei, Tong and Guo 61 ]. Here, Tz is the pump pulse duration in the crystal that may vary with propagation distance due to dispersion, called the pulse-stretching effect[ Reference Fülöp, Pálfalvi, Almási and Hebling 38 ]; Tz is regarded as a constant here since pulse-stretching in 4H-SiC can be relieved by pre-chirping the pump laser pulse[ Reference Zhong, Zhai, Li, Zhu, Li, Meng, Liu, Du, Zhao and Li 65 ]. The FCA cross-section σ is assumed to be 5 × 10–18 cm2[ Reference Grivickas, Galeckas, Grivickas and Linnros 66 ], and thus the pump absorption could be estimated by the saturated 3PA model[ Reference Gu, He, Ji and Wang 67 ] under intense pumping, where pre-chirping is also proved effective to reduce the pump absorption until negligible. Since the pump pulse duration T z and intensity I are both unchanged under pre-chirping, the free-carrier density N fc in the crystal is also regarded as invariant along the pump direction. However, compared with the pump absorption, the terahertz absorption is much more serious even if pre-chirping is present. Therefore, the terahertz absorption by free carriers α fc must be considered, which is calculated by the Drude model:
 $$\begin{align}{\alpha}_\mathrm{fc}=\frac{2\Omega}{c}\operatorname{Im}\left[\sqrt{\varepsilon_{\infty}\left(1-\frac{\omega_{\mathrm{p}}^2}{\Omega^2+i\Omega /{\tau}_\mathrm{sc}}\right)}\right],\end{align}$$
$$\begin{align}{\alpha}_\mathrm{fc}=\frac{2\Omega}{c}\operatorname{Im}\left[\sqrt{\varepsilon_{\infty}\left(1-\frac{\omega_{\mathrm{p}}^2}{\Omega^2+i\Omega /{\tau}_\mathrm{sc}}\right)}\right],\end{align}$$
where ε
∞ is the high-frequency dielectric constant, τ
sc is the electron scattering time,
![]() ${\omega}_\mathrm{p}=e\sqrt{N_\mathrm{fc}/{\varepsilon}_\mathrm{o}{\varepsilon}_{\infty }{m}_\mathrm{eff}}$
is the plasma frequency, e is the electron charge and m
eff is the electron effective mass.
${\omega}_\mathrm{p}=e\sqrt{N_\mathrm{fc}/{\varepsilon}_\mathrm{o}{\varepsilon}_{\infty }{m}_\mathrm{eff}}$
is the plasma frequency, e is the electron charge and m
eff is the electron effective mass.
3 Results and analysis
3.1 TPF OR without pre-chirping
In order to compare the performance of TPF OR in LiNbO3 and 4H-SiC, the terahertz output and pump evolution in LiNbO3 (at 100 K) and 4H-SiC (room temperature) were studied and are shown in Figure 1, respectively, both in the absence of pre-chirping. The difference between two crystals can be observed from the same low pump intensity at 50 GW/cm2, where the serious SPM and FCA effects are reflected by high-intensity pumping at 500 GW/cm2 in 4H-SiC. The FTL pump pulse durations corresponding to LiNbO3 and 4H-SiC were 350 and 30 fs, respectively, the former of which was a recognized value for LiNbO3
[
Reference Fülöp, Pálfalvi, Almási and Hebling
38
] and the latter was designated for high-frequency terahertz generation with mature ultrafast Ti:sapphire amplifiers. For comparison, the LiNbO3 crystal pumping at the FTL pulse duration of 30 fs was also studied. The other parameters are given in Table 1, where those in parentheses represent the input of LiNbO3. Note that the
![]() ${\chi}_{\mathrm{eff}}^{(2)}$
of 4H-SiC was calculated via Miller’s rule[
Reference Powers and Haus
68
] by considering d
33 = 11.7 pm/V for second harmonic generation at 1064 nm[
Reference Sato, Abe, Shoji, Suda and Kondo
69
]. The linear absorption coefficients of 4H-SiC in the optical and terahertz regions were both ignored.
${\chi}_{\mathrm{eff}}^{(2)}$
of 4H-SiC was calculated via Miller’s rule[
Reference Powers and Haus
68
] by considering d
33 = 11.7 pm/V for second harmonic generation at 1064 nm[
Reference Sato, Abe, Shoji, Suda and Kondo
69
]. The linear absorption coefficients of 4H-SiC in the optical and terahertz regions were both ignored.
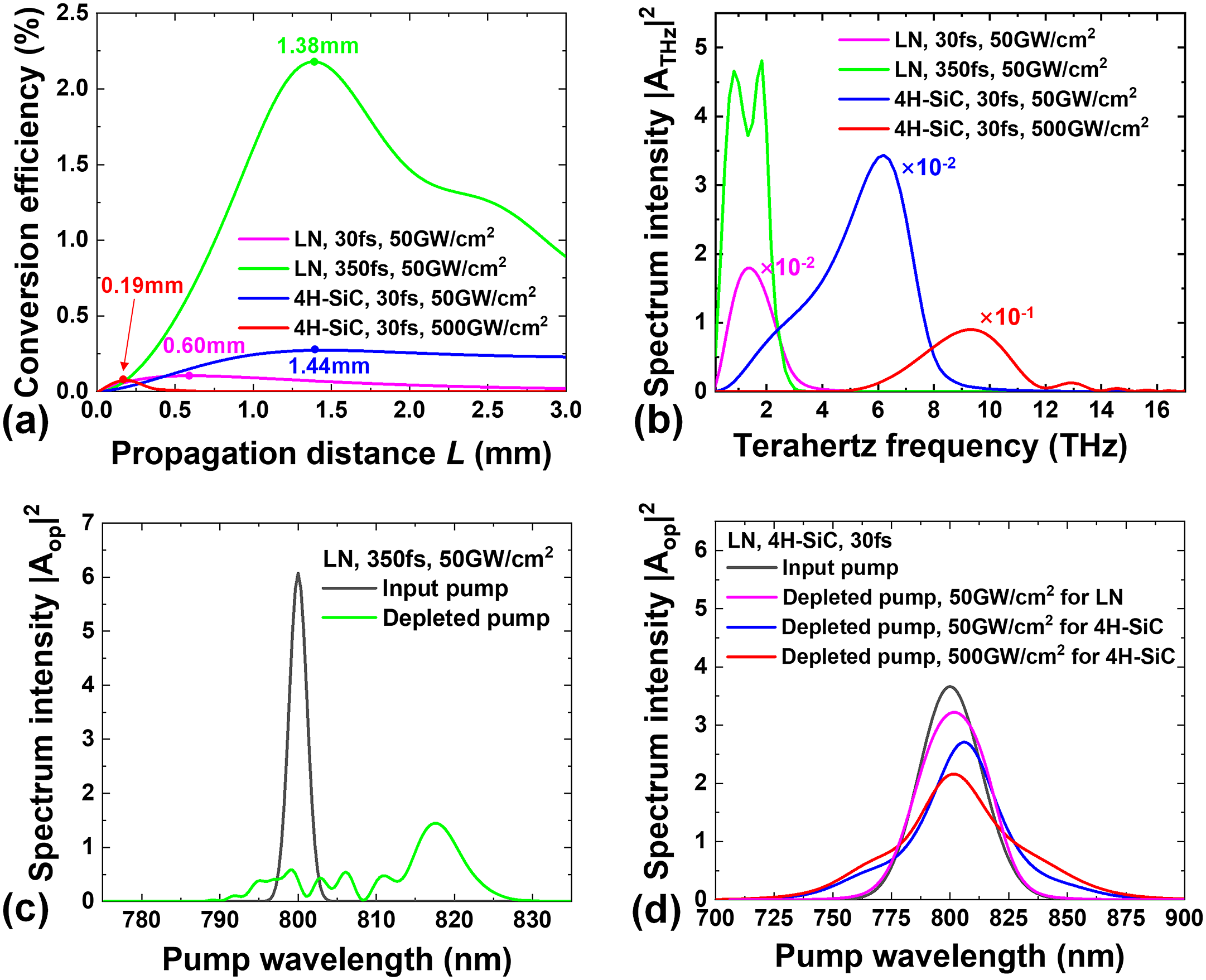
Figure 1 Comparison of terahertz output and pump evolution in LiNbO3 and 4H-SiC crystals without pre-chirping. (a) Conversion efficiencies of terahertz generation versus propagation distance L along the z direction. (b) Terahertz spectra |A THz|2 in the linear scale at the optimal L in (a), multiplied by 1, 10–2 and 10–1, respectively. (c), (d) The corresponding pump evolution processes influenced by cascading and SPM effects, including depletion, widening and frequency shift compared with the input pump. In (d), low- and high-intensity input pumps are normalized to distinguish their difference more clearly.
Table 1 Input parameters for analyzing TPF OR in LiNbO3 and 4H-SiC crystals.

According to Figure 1(a), the maximum OR efficiencies are 0.10% (at 0.60 mm), 2.18% (at 1.38 mm), 0.27% (at 1.44 mm) and 0.07% (at 0.19 mm) under the condition of LiNbO3 pumped by 30 and 350 fs pulses at 50 GW/cm2 and 4H-SiC pumped by 30 fs pulses at 50 and 500 GW/cm2, respectively. The high efficiency of LiNbO3 pumped at 350 fs originates from the strong spectral intensity and large nonlinear susceptibility. While pumping at 30 fs, the efficiency is low because a narrower FTL pulse duration corresponds to a wider spectrum, which leads to lower spectral intensity and spectral waste out of the PM bandwidth. The efficiency decline with LiNbO3 after the maximum point is mainly caused by linear absorption and back conversion, which can be observed from Figure 1(c) where shorter pump wavelengths are produced through SFG. As for 4H-SiC, the OR efficiency is extremely low with a small propagation distance L (hundred-μm level) even if the pump intensity is as high as 500 GW/cm2, because serious SPM and FCA effects limit the cascading effect and lead to strong terahertz absorption. Despite the low efficiency, the obvious advantage of 4H-SiC over LiNbO3 is apparent, that is, the capability to generate a wide terahertz spectrum benefitting from a flat dispersion curve in the terahertz range. Figure 1(b) shows the spectrum obtained at the optimal L. The terahertz frequency is extended to over 12 THz with the 4H-SiC crystal, much wider than that of LiNbO3, which is limited to below 3 THz. A shorter 4H-SiC crystal would produce an even wider spectrum, but frequencies below 5 THz are strongly absorbed by the FCA effect in the case of high-intensity pumping. Furthermore, the widening and red shift of the pump spectrum in 4H-SiC caused by the cascading effect are not apparent, as shown in Figure 1(d), but SPM dominates, which also leads to the decline of terahertz intensity, as shown in Figure 1(b). Besides, the larger red shift in Figure 1(d) implies higher conversion efficiency in Figure 1(a), even if under low-intensity pumping. Compared with 4H-SiC, the efficient cascading effect in LiNbO3 pumped at 350 fs results in remarkable spectrum widening and red shift, while SPM can be ignored[ Reference Ravi, Huang, Carbajo, Wu and Kärtner 43 ]. In contrast, the spectrum widening and red shift are both inconspicuous in LiNbO3 pumped at 30 fs, which can be explained by the low efficiency and short propagation distance. Another fact that requires consideration is the effective interaction length, which is related to the dispersion, TPF angle, FTL pulse duration, etc. It will intrinsically decrease using an ultrashort FTL pulse duration due to the dispersion in NLO crystals[ Reference Fülöp, Pálfalvi, Almási and Hebling 38 ]. Pre-chirping the incident pump pulse is an effective way to increase the effective interaction length.
3.2 TPF OR in 4H-SiC with pre-chirping
Strong SPM and FCA effects seriously limit terahertz generation under intense pumping, so that coherent terahertz radiation can only be generated in thin 4H-SiC wafers with poor efficiency. Pre-chirping the pump pulse provides an effective solution to improve the OR efficiency with at least the following advantages: (i) relieving spectrum widening originated from SPM; (ii) reducing pump and terahertz absorption caused by FCA; (iii) increasing the effective interaction length; (iv) lowering the risk of damage to the 4H-SiC crystal and other optical elements; (v) modulating the terahertz spectrum and temporal waveform, etc. A comprehensive 1D model has been developed considering the pre-chirping of the incident pump pulse, which can be realized by adding variable GDD through the acousto-optic programmable dispersion filter. The peak pump intensity is I op = 500 GW/cm2 before pre-chirping, while the other parameters are given in Table 1. Six typical TPF angles (31°, 31.5°, 32°, 33°, 35° and 38°) were simulated and analyzed with the 2D plots of OR efficiency shown in Figure 2.

Figure 2 TPF OR conversion efficiency (color scale) along the propagation distance L for various GDD values at six TPF angles from 31° to 38°. The white curves represent the maximum efficiency (η max) obtained by optimizing the GDD at each L. Areas I, II and III indicate different OR efficiencies affected by GDD, defined as excessive, insufficient and suitable pre-chirping, respectively.
Clearly, the OR efficiency is significantly improved by pre-chirping the pump pulse. The linear increase of optimal GDD with L brings the benefit that dispersion-induced pulse stretching is greatly weakened, which is consistent with the assumption of a constant pulse duration through the crystal. Tuning the TPF angle from 31° to 38° allows the generation of a higher terahertz frequency (which will be described later), accompanied by requiring more GDD at a certain L. Meanwhile, the η max curve becomes easier to saturate, gradually decreasing from more than 2% (TPF angle 31°) to 0.23% (TPF angle 38°). In order to reveal the physical process, each 2D efficiency distribution plot can be divided into three areas.
Area I: excessive pre-chirping. Pre-chirping the pump pulse results in the change of the pump spectral phase ϕ(ω), inducing the phase mismatch reflected in the Equation (1), and the OR efficiency is extremely low.
Area II: insufficient pre-chirping. SPM and FCA dominate and affect the OR efficiency. The former causes spectral widening while the latter leads to strong terahertz absorption, especially in the low-frequency range. Therefore, this area (low efficiency) is larger at smaller TPF angles.
Area III: suitable pre-chirping. The OR efficiency increases with L until saturation. Obvious efficiency oscillations can be noticed at TPF angles from 31.5° to 33° after the saturation of η max. More GDD and a larger TPF angle tend to generate more and denser oscillations. The oscillation characteristics are related to the terahertz spectrum splitting, widening and absorption, which will be explained later from viewpoint of the spectral evolution.
In order to study the influence of pre-chirping on terahertz generation and optimize the pump parameters, the 2D plots of terahertz spectrum intensity |A THz|2 versus GDD at six TPF angles are calculated and shown in Figure 3. Benefiting from the flat dispersion and high transparency of 4H-SiC in the whole terahertz band, a widely tunable terahertz spectrum can be achieved by precisely varying the TPF angle and pre-chirping. Here the optimal condition is defined as the values of GDD and L that guarantee the efficient generation of a smooth and intensity-concentrated terahertz spectrum. It can be noticed that increasing the TPF angle shifts the terahertz spectrum towards a higher frequency and shrinks the bandwidth, while the optimal GDD should be larger as well. An intense pump pulse with insufficient GDD would lead to spectral widening and terahertz absorption due to SPM and FCA effects, respectively. In particular, in the low-frequency range, more spectrum splitting and widening emerge because of the larger PM allowance together with higher absorption, resulting in declined efficiency and deterioration of the terahertz spectrum. On the other hand, excessive GDD destroys the PM condition, so that the cascading effect cannot be delivered within the L of 4 mm, showing as a rapid decline in efficiency, although the SPM and FCA are both relatively weak. In this case, effective terahertz generation requires longer L, as shown in Figure 2. In general, with the increase of GDD, the terahertz spectra experience splitting and widening with low efficiency, towards smooth and concentrated with high efficiency and, finally, decay rapidly due to the destruction of the PM condition. Only when the optimal GDD is satisfied, that is, 3900, 4200, 4500, 5050, 6000 and 7550 fs2 for the six TPF angles, respectively, can a high-quality terahertz spectrum be generated. Figure 3 shows the evolution and basic parameters to modulate a terahertz spectrum by pre-chirping the pump pulse.

Figure 3 Terahertz spectrum intensity |A THz|2 (color scale) as a function of GDD at six TPF angles from 31° (a) to 38° (f), when L = 4 mm. The white curves indicate the conversion efficiency regulated by GDD.
An intuitional demonstration of the widely tunable and smooth terahertz spectrum is shown in Figure 4, where optimal pre-chirping is applied and all the terahertz spectra are in a linear scale. Basically, the higher central terahertz frequency, the narrower the spectrum, for example, the 3-dB spectral ranges are 2.40–4.83, 3.29–6.14, 5.24–7.29, 7.71–9.05, 10.86–11.64 and 13.83–14.33 THz for the TPF angles at 31°, 31.5°, 32°, 33°, 35° and 38°, respectively. The bandwidth of the TPF angle at 31° is narrower than that at 31.5° because the FCA effect has stronger absorption to low terahertz frequencies. The FCA effect also contributes to shifting the terahertz spectrum towards the high-frequency part, as shown in Figure 4(b). The simulation results of peak frequency using the 1D model deviate more at low frequencies, which is another proof that the FCA effect has restrictions on the terahertz spectral intensity and overall efficiency in this range.

Figure 4 Spectrum tuning of TPF OR in 4H-SiC. (a) Terahertz spectrum intensity |A THz|2 at six TPF angles under optimal GDD when L = 4 mm. (b) Shift of peak frequency versus TPF angle. The black line is calculated by the PM condition cosγ = n g/n T, while the red line is simulated by the 1D model.
The evolution of terahertz spectra versus L at different TPF angles is shown in Figure 5. Consistent with the previous analysis, a lower frequency corresponds to more remarkable terahertz spectral splitting, widening and absorption due to the frequency-dependent PM allowance and FCA effect. Less GDD aggravates the absorption, resulting in more efficiency decline and spectrum deterioration after reaching the maximum efficiency. It can be observed that there is similar oscillation and attenuation in efficiency to that shown in Figure 2. The oscillation period and amplitude depend on the PM bandwidth, reflecting the speed and strength of spectrum splitting and widening, while the efficiency attenuation mainly originates from FCA. Specially, obvious attenuation rather than oscillation appears at the low-frequency part due to serious absorption (TPF angle ≤ 33°). As for the high-frequency part (TPF angle ≥ 33°), there is neither obvious oscillation nor efficiency attenuation due to the small PM bandwidth and absorption. The simulation results also accord with Figure 3 very well. With the increase of L, it fails to produce a terahertz spectrum effectively under excessive pre-chirping, and reaches the optimal condition at L = 4 mm. Finally, spectrum splitting, widening and attenuation under insufficient pre-chirping appear, especially for the low-frequency part at the small TPF angle.

Figure 5 The evolution of terahertz spectrum intensity |A THz|2 (color scale) along the propagation distance L at six TPF angles, under optimal GDD and at L = 4 mm. The white curve indicates the conversion efficiency as a function of L.
For a better understanding of the evolution of terahertz radiation with L under pre-chirping, the terahertz spectrum and temporal waveform at two different conditions are analyzed, as shown in Figure 6. For the first case, γ = 31.5° and GDD = 4200 fs2, and the results are given in Figures 6(a) and 6(b). When L is short (e.g., 1.5 mm), only low frequencies centered at 1.6 THz are generated and the spectral intensity is very low due to excessive pre-chirping, corresponding to a single-cycle terahertz pulse with the electric field amplitude of approximately 0.1 MV/cm. As the interaction continues in a longer crystal, the terahertz pulse grows stronger and transforms into multi-cycle. The subsequent denser cycles are amplified faster, corresponding to the shift of peak frequency towards the higher frequency range (desired terahertz frequency at γ = 31.5°) and increase the spectrum intensity gradually. When L = 4 mm, the electric field amplitude of the multi-cycle pulse reaches approximately 1 MV/cm with an intensity-concentrated spectrum. If L is further increased to beyond the optimal value (e.g., 5.8 mm, the next oscillation peak in Figure 5), both the spectrum and temporal waveform are split and widened because of insufficient pre-chirping, as well as more absorption to lower frequencies. We can notice that there is only one continuous terahertz pulse throughout the crystal. However, the evolution of high-frequency terahertz waves includes two independent temporal pulses in the crystal, which is the second case. Taking γ = 33° and GDD = 5050 fs2, for example, the results are shown in Figures 6(c) and 6(d). Similar to the previous discussion, when the pre-chirped pulse just enters the crystal, the terahertz pulse was single-cycle and only low frequencies were produced. With a longer propagation distance (e.g., 2.87 mm), periodical oscillation starts to appear after the initial single-cycle pulse, forming the other temporal pulse shown in Figure 6(d). The second pulse mainly contributes to the high-frequency range and greatly widens the spectral width together with the initial one, although the spectral intensity is still low. When L reaches the optimal value of 4 mm, we can observe the initial terahertz pulse and a clear amplified multi-cycle pulse in the temporal waveform. This proves that the generation and evolution of these two terahertz pulses are independent of each other. If L exceeds the optimal value (e.g., 4.85 mm, the next oscillation peak in Figure 5), both the terahertz spectrum and temporal waveform become split and widened, similar to the first case.

Figure 6 The evolution of the terahertz spectrum ((a) and (c)) and temporal waveform ((b) and (d)) with L at two different conditions: (a), (b) γ = 31.5°, GDD = 4200 fs2; (c), (d) γ = 33°, GDD = 5050 fs2. The former forms only one continuous terahertz pulse throughout the crystal, while the latter forms two independent pulses.
Based on the above analysis, a scheme to modulate terahertz generation by pre-chirping can be proposed. Given γ = 32° and L = 4 mm, the terahertz spectra and temporal waveforms with different GDDs are as shown in Figure 7. The optimal GDD of 4500 fs2 corresponds to an efficient, smooth and concentrated terahertz spectrum with strong multi-cycle electric field amplitude up to approximately 0.8 MV/cm. Tuning the GDD to 7000 fs2 leads to the generation of a near single-cycle terahertz pulse (~0.2 MV/cm) with a narrow spectrum centering at 1.4 THz. If the GDD is varied to 6000 fs2, a flat-top broadband terahertz spectrum (1–7.5 THz, full width at half maximum (FWHM)) can be obtained with considerably high intensity. Note that the bandwidth can be even wider under a larger TPF angle, but the spectral intensity and flatness will be degraded, similar to the above situation of γ = 33°. When the GDD is reduced to 3500 fs2, it turns into a split and widened terahertz spectrum and temporal waveform, in which the low-frequency part suffers attenuation due to the FCA effect.

Figure 7 Modulation of the terahertz spectra (a) and temporal waveform (b) by varying pre-chirping when γ = 32° and L = 4 mm. Different terahertz spectra (flat-top broadband, efficient and concentrated, split and widened) and temporal waveforms (single- to multi-cycle pulses) can be flexibly tuned by varying the GDD.
Generally, generating high-frequency terahertz waves by TPF OR in 4H-SiC is always accompanied by more and narrower temporal cycles with suitable GDD, which is demonstrated in Figure 6. Since the central frequency is tunable by the TPF angle, two typical cases, γ = 31° and γ = 38°, are discussed and the simulation results are shown in Figure 8. The GDDs are 800, 4000 and 8000 fs2 for both cases, while the optimal L values are 0.62, 4.12 and 8 mm for γ = 31°, and 0.445, 2.1 and 4.19 mm for γ = 38°, respectively. A larger GDD with longer L excites more pulse cycles and a longer pulse duration, corresponding to a narrower and more concentrated terahertz spectrum. The blue shift of the terahertz spectrum and low-frequency attenuation in Figure 8(a) are caused by a strong FCA effect with low pre-chirping, while FCA exhibits little influence in Figure 8(c) because the high-frequency absorption by photocarriers is relatively weak. It is further confirmed here that a higher frequency corresponds to a narrower temporal cycle, where the cycle intervals for γ = 31° and γ = 38° are around 200 and 70 fs, respectively. The generation of a multi-cycle terahertz pulse can be explained by the fact that the pump pulse is intensity-resonant, modulated by the initial pre-chirping and self-produced terahertz fields, which in turn produce multi-cycle terahertz waves efficiently during the interaction[ Reference Jang and Kim 47 ]. According to Figure 2, the maximum efficiency η max for γ = 38° stops increasing at L ≈ 1 mm so that the terahertz field amplitude would decrease to produce more pulse cycles and a longer duration. It reveals the method of effective modulation on a terahertz spectrum and waveform by pre-chirping (at optimal L), that is, even if the OR efficiency is saturated, a narrower but more concentrated terahertz spectrum with the temporal waveform of more cycles is still achievable by increasing the pre-chirping and L. The envelope fluctuation and enlarged interval between the initial pulse and the long multi-cycle pulse are observed with larger GDD and L, as shown in Figure 8(d). This phenomenon is also ascribed to the NLO interaction between the highly pre-chirped pump pulse and terahertz fields through adequate propagation distance. Compared with the other methods for multi-cycle terahertz generation, for example, OR in periodically poled lithium niobate (PPLN)[ Reference L’huillier, Torosyan, Theuer, Avetisyan and Beigang 70 , Reference Carbajo, Schulte, Wu, Ravi, Schimpf and Kärtner 71 ], with intensity-modulated laser pulses[ Reference Tóth, Fülöp and Hebling 72 , Reference Nugraha, Krizsán, Polónyi, Mechler, Hebling, Tóth and Fülöp 73 ] and with chirped laser pulses[ Reference Jang and Kim 47 ], the distinct advantages of TPF OR in 4H-SiC include ultra-widely tunable bandwidth and flexibility in manipulating the temporal waveform, which is of significant value in terahertz-driven X-ray sources[ Reference Kärtner, Ahr, Calendron, Çankaya, Carbajo, Chang, Cirmi, Dörner, Dorda, Fallahi, Hartin, Hemmer, Hobbs, Hua, Huang, Letrun, Matlis, Mazalova, Mücke, Nanni, Putnam, Ravi, Reichert, Sarrou, Wu, Yahaghi, Ye, Zapata, Zhang, Zhou, Miller, Berggren, Graafsma, Meents, Assmann, Chapman and Fromme 74 ], compact accelerators[ Reference Liu, Sun, Yu, Liu, Jia, Sun and Xu 7 , Reference Wong, Fallahi and Kärtner 75 – Reference Matlis, Ahr, Calendron, Cankaya, Cirmi, Eichner, Fallahi, Fakhari, Hartin, Hemmer, Huang, Ishizuki, Jolly, Leroux, Maier, Meier, Qiao, Ravi, Schimpf, Taira, Wu, Zapata, Zapata, Zhang, Zhou and Kärtner 77 ], resonant control over materials[ Reference Kampfrath, Tanaka and Nelson 3 ], etc.

Figure 8 Terahertz spectrum ((a) and (c)) and temporal waveform ((b) and (d)) at different TPF angles (γ = 31° and γ = 38°) and pre-chirping (GDD = 800, 4000 and 8000 fs2) at the corresponding optimal L. The insets in (d) show the initially established terahertz signal when the pre-chirped pump pulse enters the crystal.
4 Conclusion
Considering the excellent physical and optical properties of 4H-SiC, TPF OR based on this crystal was studied for the first time via the 1D model, accounting for coupled NLO interaction of the terahertz and optical waves, AD and MD, linear absorption, FCA at the terahertz frequency, SPM and pre-chirping of the pump pulse. Compared with LiNbO3, 4H-SiC-based TPF OR demonstrates great potential in producing ultra-widely tunable (up to over 14 THz) terahertz waves with high efficiency (~10–2) and strong field (~MV/cm), while the TPF angle is only half of that in LiNbO3. The terahertz field can be further enhanced by focusing in experiments. The small TPF angle is a significant advantage to increase the effective interaction length and spatial uniformity, and reduce the GVD-AD and beam distortion, which greatly favors the contact grating (CG) design[ Reference Polónyi, Monoszlai, Andriukaitis, Gäumann, Balciunas, Pugzlys, Baltuska, Feurer, Hebling and Fülöp 21 , Reference Bakunov and Bodrov 42 , Reference Ollmann, Fülöp, Hebling and Almási 49 ]. Pre-chirping the pump pulse was proved effective in modulating the terahertz spectrum and temporal pulse waveform. Flat-top broadband, efficient and concentrated or split and widened spectra are flexibly tunable by presetting the TPF angle, GDD and L properly. The corresponding terahertz pulse can be single-cycle or multi-cycle with the minimum interval of tens of femtoseconds. 4H-SiC-based TPF OR has extremely important potential in strong-field and ultra-wide bandwidth terahertz applications, including nonlinear terahertz spectroscopy, strong-field terahertz physics, electron acceleration, etc. In particular, the multi-cycle terahertz pulse combines high acceleration gradient and long interaction distance, which is favorable for waveguide-based electron acceleration[ Reference Wong, Fallahi and Kärtner 75 , Reference Zhang, Zeng, Fakhari, He, Matlis and Kärtner 76 ]. The multi-cycle narrowband terahertz pulse in the high-frequency range also provides a good solution for compact and efficient acceleration structures[ Reference Matlis, Ahr, Calendron, Cankaya, Cirmi, Eichner, Fallahi, Fakhari, Hartin, Hemmer, Huang, Ishizuki, Jolly, Leroux, Maier, Meier, Qiao, Ravi, Schimpf, Taira, Wu, Zapata, Zapata, Zhang, Zhou and Kärtner 77 ]. It should be noted that since 4H-SiC is a commercialized material in the semiconductor industry, large size crystals are readily available, benefitting from the mature growing and manufacturing technology, so that scaling the terahertz pulse energy is straightforward as long as the pump laser is powerful enough.
Acknowledgement
This work was supported by the National Natural Science Foundation of China (No. 62175184) and the Key Laboratory of Micro Opto-electro Mechanical System Technology, Ministry of Education.












