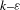1. Introduction
High-power laser systems (HPLSs) are large optical instruments for high-energy physics and inertial confinement fusion. The transport mirrors of HPLSs direct light from the main amplifiers to the target and impact remarkably upon the quality of laser beams arriving at the target[Reference Norton, Stolz, Donohue, Listiyo, Pryatel and Hackel1]. Current mirrors work at a fluence of several joules per square centimeter, but future operating conditions will require these mirrors to sustain high fluences of up to tens of joules per square centimeter or even higher. Therefore, rigorous cleanliness is critical in preventing damage to the mirror surfaces and prolonging the lifetime of the optical devices[Reference Gourdin, Dzenitis, Martin, Listiyo, Sherman, Kent, Butlin, Stolz and Pryatel2].
The debris on mirrors includes natural dust falls, metal fragments, and organic fibers left during operations. Numerous methods have been used to keep the optical devices clean, but to date, few experimental results have demonstrated the optical cleanliness of the whole laser facility[Reference Wang, Wang, Zhu, Chen and Wu3]. Wiping mirrors with a clean cloth is the commonly practiced technique. However, hard debris often scratches transport mirrors because uneven forces are used in wiping away debris. Thus, the Lawrence Livermore National Laboratory designed an in situ surface debris-removal system for the upward-facing transport mirrors of the National Ignition Facility. This system effectively removes debris with particle sizes larger than ![]() $10~{\rm\mu}\text{m}$ using high-speed airflow generated by an air knife[Reference Gourdin, Dzenitis, Martin, Listiyo, Sherman, Kent, Butlin, Stolz and Pryatel2, Reference Stolz4, Reference Stolz5]. However, most of the debris returns to the environment, which easily leads to the contamination of other optical components and re-contamination of the mirrors. Therefore, understanding debris-removal trajectories and realizing the capture and collection of the debris during the blowing process are necessary for efficient debris removal.
$10~{\rm\mu}\text{m}$ using high-speed airflow generated by an air knife[Reference Gourdin, Dzenitis, Martin, Listiyo, Sherman, Kent, Butlin, Stolz and Pryatel2, Reference Stolz4, Reference Stolz5]. However, most of the debris returns to the environment, which easily leads to the contamination of other optical components and re-contamination of the mirrors. Therefore, understanding debris-removal trajectories and realizing the capture and collection of the debris during the blowing process are necessary for efficient debris removal.
In the present study, the flow field and the removal trajectories of debris with varied types and sizes on the transport mirror are numerically investigated. A device is fabricated based on the simulation results. This device can capture and collect debris from the mirror surface online.
2. The numerical model
Computational fluid dynamics (CFD) is an important technique for investigating flow fields. With computer numerical calculation and image display, CFD can conduct numerical simulations on a system containing relevant physical phenomena, such as fluid flow and heat. Numerical analysis of the flow field with basic physical quantities (such as speed, pressure, temperature and concentration), as well as the distribution of fluid trajectory, is now a popular topic in fluid studies.

Figure 1. Interaction force between the gas and a spherical particle.

Figure 2. Schematic diagram of air ejection.

Figure 3. Model of the air knife blowing.
2.1. The model to be calculated
A two-dimensional (2D) model satisfies the requirements of understanding the fluid field and the trajectories of contaminant particles. The 2D model in this study included one air knife, one transport mirror and one cover (Figure 1). The air knife was used to provide high-speed airflow. The transmission mirror surface, covered with particulate pollutants, was the purged surface. The cover connecting to a vacuum cleaner was used to provide a low pressure area, change the flow field and realize the capture of contaminant particles. Several assumptions were considered to simplify the model. First, the fluid was compressible nitrogen, which provided a stable inlet pressure. Second, the loaded solid particles were spheres with smooth surfaces. Similar solid particles had similar densities. No energy was lost during the particle and wall collisions, and the rebounds were symmetrical. Third, only the steady aerodynamic resistances affecting the solid particles caused by the fluid flow were considered, and the Basset and Saffman forces were ignored.
The 2D model was implemented using the business software Gambit 2.4.6, used for geometry and mesh generation, and the 20 640 quadrilateral elements were divided by quadrilateral mesh structures[Reference Ruijin, Kai and Gang6, Reference Zhanzhong7]. The coupled implicit solver, steady-state calculations and second-order upwind discretization were adopted. The Courant number was 1. The simulation of the gas–solid flow field was calculated using the discrete phase model. The convergence criteria of the mass residuals and energy residuals were less than ![]() $10^{-5}$.
$10^{-5}$.
2.2. Boundary conditions and associated settings
The best way to remove a particle is to blow in the direction of the ![]() $x$-axis, where the particle can be subjected to maximum thrust
$x$-axis, where the particle can be subjected to maximum thrust ![]() $R$ (Figure 2). The airflow ejecting from the nozzle is similar to a trapezoidal distribution (Figure 3). The maximum speed of the cross-section is at the center line (
$R$ (Figure 2). The airflow ejecting from the nozzle is similar to a trapezoidal distribution (Figure 3). The maximum speed of the cross-section is at the center line (![]() $x$-axis). Thus, the particle is subjected to the maximum force and easily removed when the blowing surface is situated on the
$x$-axis). Thus, the particle is subjected to the maximum force and easily removed when the blowing surface is situated on the ![]() $x$-axis. Therefore, a suitable distance
$x$-axis. Therefore, a suitable distance ![]() $S$ between the up-surfaces of the transport mirror and the air knife was chosen to make the transport mirror surface close to, or coinciding with, the centerline of the airflow (Figure 1). Thus, a suitable air pressure should be selected to obtain a suitable flow velocity. Figure 1 shows that after ejecting from the air knife, the airflow initially flowed along the curved edge of the air knife, then the flow direction changed to
$S$ between the up-surfaces of the transport mirror and the air knife was chosen to make the transport mirror surface close to, or coinciding with, the centerline of the airflow (Figure 1). Thus, a suitable air pressure should be selected to obtain a suitable flow velocity. Figure 1 shows that after ejecting from the air knife, the airflow initially flowed along the curved edge of the air knife, then the flow direction changed to ![]() $90^{\circ }$. Finally, the airflow entered the up-surface
$90^{\circ }$. Finally, the airflow entered the up-surface ![]() $L$ of the transport mirror and moved along the up-surface. After a series of experiments, a good particle removal effect was obtained when the air pressure was 9 atm and
$L$ of the transport mirror and moved along the up-surface. After a series of experiments, a good particle removal effect was obtained when the air pressure was 9 atm and ![]() $S$ was 3 mm.
$S$ was 3 mm.

Figure 4. Simulation results of the flow.
Boundary conditions were set as follows. The outlet of the air knife was the pressure inlet. The gage total pressure was 9 atm, the supersonic/initial gage total pressure was 7 atm, the inlet temperature was 300 K and the turbulent energy and default dissipation rates were 1.
Boundaries ![]() $H$,
$H$, ![]() $N$,
$N$, ![]() $D$, and
$D$, and ![]() $T$ were the pressure outlets.
$T$ were the pressure outlets. ![]() $H=423.05~\text{mm}$,
$H=423.05~\text{mm}$, ![]() $N=50~\text{mm}$,
$N=50~\text{mm}$, ![]() $D=32~\text{mm}$, and
$D=32~\text{mm}$, and ![]() $T=8~\text{mm}$. The outlet temperature was 300 K. The turbulent energy and default dissipation rate were 1. The gage total pressures of boundaries
$T=8~\text{mm}$. The outlet temperature was 300 K. The turbulent energy and default dissipation rate were 1. The gage total pressures of boundaries ![]() $H$,
$H$, ![]() $N$,
$N$, ![]() $D$ and
$D$ and ![]() $T$ were 1 atm. The gage total pressure of boundary
$T$ were 1 atm. The gage total pressure of boundary ![]() $D$ was 0.8 atm.
$D$ was 0.8 atm.
The remaining boundaries were walls, which were non-slip walls. ![]() $K=21.05~\text{mm}$,
$K=21.05~\text{mm}$, ![]() $T=8~\text{mm}$, and the length
$T=8~\text{mm}$, and the length ![]() $L$ of the up-surface of the transport mirror was 400 mm. Dust, aluminum particles and stainless steel particles, with sizes of 10, 20, 40, and 80
$L$ of the up-surface of the transport mirror was 400 mm. Dust, aluminum particles and stainless steel particles, with sizes of 10, 20, 40, and 80 ![]() $~{\rm\mu}\text{m}$, were used as debris, and they were uniformly distributed on the surface of the transport mirror. The densities of dust, aluminum (Al) particles and stainless steel (ss) particles were 1000, 2700 and
$~{\rm\mu}\text{m}$, were used as debris, and they were uniformly distributed on the surface of the transport mirror. The densities of dust, aluminum (Al) particles and stainless steel (ss) particles were 1000, 2700 and ![]() $7930~\text{kg m}^{-3}$, respectively.
$7930~\text{kg m}^{-3}$, respectively.
2.3. Governing equations
The basic equations of fluid analysis, turbulent flow and particle motion were used as the control equations[Reference Fujun8]. These basic equations included the equations for the conservation of mass, momentum and energy. The turbulent flow model was the RNG ![]() $k{-}{\it\varepsilon}$ model, which is an improved model of the standard turbulent model of
$k{-}{\it\varepsilon}$ model, which is an improved model of the standard turbulent model of ![]() $k{-}{\it\varepsilon}$. The particle motion equation was the force-balance equation in Cartesian coordinates.
$k{-}{\it\varepsilon}$. The particle motion equation was the force-balance equation in Cartesian coordinates.
3. Simulation results and discussion
3.1. Flow field
Figures 4 and 5 are the simulation results of the whole flow and the vector of the flow near the air knife. The maximum speed of the air flow coming from the air knife reaches ![]() $575~\text{m}~\text{s}^{-1}$ in the region near the outlet of the air knife (Figure 4). Air velocity decreases along the wall from the outlet of the air knife to the far end of the transport mirror with the length of 400 mm. Figure 6 is the velocity of pressure outlet
$575~\text{m}~\text{s}^{-1}$ in the region near the outlet of the air knife (Figure 4). Air velocity decreases along the wall from the outlet of the air knife to the far end of the transport mirror with the length of 400 mm. Figure 6 is the velocity of pressure outlet ![]() $D$. The negative pressure of outlet
$D$. The negative pressure of outlet ![]() $D$ can steer flow. The air speed is
$D$ can steer flow. The air speed is ![]() $115~\text{m}~\text{s}^{-1}$, which approximately decreases along the
$115~\text{m}~\text{s}^{-1}$, which approximately decreases along the ![]() $y$-axis. These high speeds blow the particles away from the transport mirror.
$y$-axis. These high speeds blow the particles away from the transport mirror.

Figure 5. Velocity vector of the flow near the air knife.

Figure 6. Speed of the flow at the pressure outlet ![]() $D$ in the
$D$ in the ![]() $y$-axis.
$y$-axis.
3.2. Debris trajectories
Dust particles with four different sizes were considered. For each size, 200 dust particles were evenly placed on the transport mirror up-surface ![]() $L$ from the left to the right, and a numerical simulation was performed based on the numerical model and settings stated in Section 2. The removal trajectories of dust particles were obtained (Figure 7). Figure 7(a)–(d) correspond to the particles with sizes of 10, 20, 40 and
$L$ from the left to the right, and a numerical simulation was performed based on the numerical model and settings stated in Section 2. The removal trajectories of dust particles were obtained (Figure 7). Figure 7(a)–(d) correspond to the particles with sizes of 10, 20, 40 and ![]() $80~{\rm\mu}\text{m}$, respectively. Each curve represents one type of movement tendency of some particles. There are a total of three kinds of movement trends: type 1, type 2 and type 3. Besides this, curves of type 1 in Figure 7(a) and (b), and curves of type 3 in Figure 7(c) and (d), are also corresponding in respect of the maximum trajectories of particles in four sizes.
$80~{\rm\mu}\text{m}$, respectively. Each curve represents one type of movement tendency of some particles. There are a total of three kinds of movement trends: type 1, type 2 and type 3. Besides this, curves of type 1 in Figure 7(a) and (b), and curves of type 3 in Figure 7(c) and (d), are also corresponding in respect of the maximum trajectories of particles in four sizes.

Figure 7. Trajectories of dust particles in four sizes. The sizes of the dust particles in (a)–(d) correspond to 10, 20, 40 and ![]() $80~{\rm\mu}\text{m}$.
$80~{\rm\mu}\text{m}$.
The simulation results demonstrate that the motion displacements of the majority of the particles are small in the vertical direction, almost slipping along the upper surface of the mirror (type 2). The ![]() $y$-coordinate of the upper mirror surface is 2 mm; thus the minimum value of
$y$-coordinate of the upper mirror surface is 2 mm; thus the minimum value of ![]() $Y$ in Figure 7 is 2 mm. Only 10 particles (type 1 and type 3) have different trajectories compared with the other particles because the static pressure in most of the mirror surface area is greater than or equal to the standard atmospheric pressure, except for the area that is 0 to 6 mm away from the mirror edge closing to the air knife (Figure 8). The pressure is negative in this area, and 10 particles labeled 0 to 9 are distributed in this area.
$Y$ in Figure 7 is 2 mm. Only 10 particles (type 1 and type 3) have different trajectories compared with the other particles because the static pressure in most of the mirror surface area is greater than or equal to the standard atmospheric pressure, except for the area that is 0 to 6 mm away from the mirror edge closing to the air knife (Figure 8). The pressure is negative in this area, and 10 particles labeled 0 to 9 are distributed in this area.

Figure 8. Hydrostatic transmission curve on the mirror surface.

Figure 9. Maximum ![]() $Y$ values of three particle types in four sizes. The sizes of the particles in (a)–(d) correspond to 10, 20, 40, and
$Y$ values of three particle types in four sizes. The sizes of the particles in (a)–(d) correspond to 10, 20, 40, and ![]() $80~{\rm\mu}\text{m}$.
$80~{\rm\mu}\text{m}$.
The ![]() $Y$ values of particles increase rapidly, decrease, then increase along the path, and finally decrease (type 1). This event is due to the fact that the region of the 10 particles instantly becomes a negative pressure zone when the air knife is blowing. Then, turbulences (Figure 5) occur and drive the particles to instantly generate upward movements. With the increase in the
$Y$ values of particles increase rapidly, decrease, then increase along the path, and finally decrease (type 1). This event is due to the fact that the region of the 10 particles instantly becomes a negative pressure zone when the air knife is blowing. Then, turbulences (Figure 5) occur and drive the particles to instantly generate upward movements. With the increase in the ![]() $Y$ values, the pneumatic forces weaken, gravity gradually dominates, and the velocities decrease to zero. During this period, the
$Y$ values, the pneumatic forces weaken, gravity gradually dominates, and the velocities decrease to zero. During this period, the ![]() $Y$ values reach maximum. Then, the particles move along the negative direction of the
$Y$ values reach maximum. Then, the particles move along the negative direction of the ![]() $y$-axis, the
$y$-axis, the ![]() $Y$ values decrease, and the vortices are strengthened. The velocities of the particles along the negative direction of the
$Y$ values decrease, and the vortices are strengthened. The velocities of the particles along the negative direction of the ![]() $y$-axis are gradually reduced to zero when the pneumatic forces are large enough to overcome gravity. Then, the velocity direction reverses, and the
$y$-axis are gradually reduced to zero when the pneumatic forces are large enough to overcome gravity. Then, the velocity direction reverses, and the ![]() $Y$ values increase. Gradually, the
$Y$ values increase. Gradually, the ![]() $Y$ values decrease because the negative pressure of the outlet
$Y$ values decrease because the negative pressure of the outlet ![]() $D$ can steer flow.
$D$ can steer flow.
With the increase in particle sizes, the numbers of particles of type 3 that begin to reach the maximum ![]() $Y$ values, hit the mirror surface and finally rebound off the surface also increase. This phenomenon is due to insufficient pneumatic forces to overcome the additional gravity caused by the increase in the particle sizes in the falling phase, and more particles crash into the mirror surface and rebound off. The maximum
$Y$ values, hit the mirror surface and finally rebound off the surface also increase. This phenomenon is due to insufficient pneumatic forces to overcome the additional gravity caused by the increase in the particle sizes in the falling phase, and more particles crash into the mirror surface and rebound off. The maximum ![]() $Y$ value is 19.1 mm and the size of the dust is
$Y$ value is 19.1 mm and the size of the dust is ![]() $80~{\rm\mu}\text{m}$ at the moment when the four sizes of particles are present.
$80~{\rm\mu}\text{m}$ at the moment when the four sizes of particles are present.
Similar results are also obtained when numerical simulations are conducted for stainless steel and aluminum particles in four sizes. The corresponding maximum ![]() $Y$ values are 23.6 and 24 mm, and their sizes are both
$Y$ values are 23.6 and 24 mm, and their sizes are both ![]() $80~{\rm\mu}\text{m}$.
$80~{\rm\mu}\text{m}$.
Comparing the maximum ![]() $Y$ values of the dust, the aluminum particles and the stainless steel particles, the greater the particle density, the greater the maximum
$Y$ values of the dust, the aluminum particles and the stainless steel particles, the greater the particle density, the greater the maximum ![]() $Y$ value when the particles are of the same size (Figure 9).
$Y$ value when the particles are of the same size (Figure 9).
4. The device
A device was designed based on the above model of the air knife (Figure 1). The device had the same boundary conditions and associated settings as those mentioned above. The device could capture and collect contaminant particles (Figure 10). The cover was connected to a vacuum cleaner, which provided a negative pressure. The device performance was tested using dust particles with sizes that ranged from 25 to ![]() $50~{\rm\mu}\text{m}$ and 50 to
$50~{\rm\mu}\text{m}$ and 50 to ![]() $100~{\rm\mu}\text{m}$ as the contaminants, because most contaminant particles on the transport mirror are dust.
$100~{\rm\mu}\text{m}$ as the contaminants, because most contaminant particles on the transport mirror are dust.

Figure 10. Layout of the device. #1, #2, #3, #4, and #5 are transport mirrors.
Table 1. The numbers of particles before and after blowing.

Ordinary glass with the size of ![]() $300~\text{mm}\times 400~\text{mm}$ was used as a substitute for the transport mirrors. The glass was divided into four pieces to facilitate the measurement of the number of dust particles using a microscope. Each piece had the same size of
$300~\text{mm}\times 400~\text{mm}$ was used as a substitute for the transport mirrors. The glass was divided into four pieces to facilitate the measurement of the number of dust particles using a microscope. Each piece had the same size of ![]() $150~\text{mm}\times 200~\text{mm}$. Circular measurement areas of
$150~\text{mm}\times 200~\text{mm}$. Circular measurement areas of ![]() $4\times 4$ with a diameter of 10 mm were set. Positioning centers represented by ‘
$4\times 4$ with a diameter of 10 mm were set. Positioning centers represented by ‘![]() $+$’ were distributed on the opposites of the measurement surfaces (Figure 11). The total number of particles measured in the 16 regions represented the number of particles on the mirror surface to reduce experimental errors. Four clean mirrors surrounded mirror #1 to monitor and judge the moving trend of the dust particles during air blowing. The air knife used was a commercial air knife type 12014s[9]. The distance
$+$’ were distributed on the opposites of the measurement surfaces (Figure 11). The total number of particles measured in the 16 regions represented the number of particles on the mirror surface to reduce experimental errors. Four clean mirrors surrounded mirror #1 to monitor and judge the moving trend of the dust particles during air blowing. The air knife used was a commercial air knife type 12014s[9]. The distance ![]() $S$ from the upper mirror surface to the upper air knife surface was 3 mm (Figures 1 and 10). The inlet pressure was 9 atm. The changes in the number of dust particles on the surfaces of the mirrors before and after using the device were determined. The cover provided a negative pressure of 0.8 atm during blowing. Experiments were conducted in an ultra-clean environment with a cleanliness level of class 1000.
$S$ from the upper mirror surface to the upper air knife surface was 3 mm (Figures 1 and 10). The inlet pressure was 9 atm. The changes in the number of dust particles on the surfaces of the mirrors before and after using the device were determined. The cover provided a negative pressure of 0.8 atm during blowing. Experiments were conducted in an ultra-clean environment with a cleanliness level of class 1000.

Figure 11. Sample of the transport mirror.
The experimental results are shown in Table 1. When a debris collector is not used, the numbers of particles in the particle size ranges of ![]() $25{-}50~{\rm\mu}\text{m}$ and
$25{-}50~{\rm\mu}\text{m}$ and ![]() $50{-}100~{\rm\mu}\text{m}$ are reduced from 612 to 97 and from 632 to 55 respectively after blowing. The efficiency of the air knife clearance of dust particles in the two ranges is 84% and 91%, respectively. These percentages indicate that the air knife can efficiently remove stainless steel particles. At this time, 12% and 4% of the dust particles in the two size ranges are transferred to the surfaces of #2, #3, #4 and #5 transport mirrors. Many particles on the surface of transport mirror #1 are transferred to the surrounding environment in the blowing process.
$50{-}100~{\rm\mu}\text{m}$ are reduced from 612 to 97 and from 632 to 55 respectively after blowing. The efficiency of the air knife clearance of dust particles in the two ranges is 84% and 91%, respectively. These percentages indicate that the air knife can efficiently remove stainless steel particles. At this time, 12% and 4% of the dust particles in the two size ranges are transferred to the surfaces of #2, #3, #4 and #5 transport mirrors. Many particles on the surface of transport mirror #1 are transferred to the surrounding environment in the blowing process.
However, the numbers of particles in the particle size ranges of ![]() $25{-}50~{\rm\mu}\text{m}$ and
$25{-}50~{\rm\mu}\text{m}$ and ![]() $50{-}100~{\rm\mu}\text{m}$ are reduced from 495 to 79 and from 668 to 43 respectively after blowing when a debris collector is used. This result indicates that the removal efficiency of dust particles in the two ranges is 84% and 94%, which is better than the case without a debris collector. Therefore, using a debris collector can improve removal efficiency. Additionally, 9% and 1% of the dust particles in the two size ranges transfer to the surfaces of #2, #3, #4 and #5 transport mirrors, and these percentages are lower than the case without the debris collector. This result suggests that the debris collector can collect dust particulates and reduce the probability that particles transfer to the surrounding environment, and partly validates the simulation results of the debris-removal trajectories.
$50{-}100~{\rm\mu}\text{m}$ are reduced from 495 to 79 and from 668 to 43 respectively after blowing when a debris collector is used. This result indicates that the removal efficiency of dust particles in the two ranges is 84% and 94%, which is better than the case without a debris collector. Therefore, using a debris collector can improve removal efficiency. Additionally, 9% and 1% of the dust particles in the two size ranges transfer to the surfaces of #2, #3, #4 and #5 transport mirrors, and these percentages are lower than the case without the debris collector. This result suggests that the debris collector can collect dust particulates and reduce the probability that particles transfer to the surrounding environment, and partly validates the simulation results of the debris-removal trajectories.
5. Conclusions
In the present study, numerical simulations of debris-removal trajectories on the transport mirrors of HPLSs are conducted using Fluent commercial software. The trajectories of contaminant particles of different sizes and types on the transport mirror surface are determined. A device is built based on the simulation results to efficiently capture and collect debris from the surface of the mirror online. Ultimately, debris contamination of other optical components is avoided, cleaning time is shortened and the cleanliness of the mirrors is ensured. Only mirrors laid horizontally have been considered in the present work. Although many transport mirrors are laid non-horizontally in practical applications, more studies are required to understand the debris-removal trajectories of horizontal mirrors. Meanwhile, the cover should also be optimized to capture and efficiently collect debris particles, and further verify the simulation results of the debris trajectories.
Acknowledgements
The authors would like to acknowledge Dr Mingying Sun for modifying and proofreading the manuscript. Grants from the Chinese and Israeli cooperation project on high-power laser technology (2010DFB70490) supported this study.