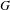1 Introduction
K-shell lines of elements from astrophysical X-ray sources have been widely identified in high-resolution spectra, which are observed by X-ray satellites, such as Chandra and XMM-Newton. There are not only strong emission lines from photoionized plasmas of X-ray binaries[Reference Ji, Schulz, Nowak, Marshall and Kallman1–Reference Jimenez-Garate, Hailey, den Herder, Zane and Ramsay3], but also absorption lines from active galactic nuclei (AGNs)[Reference Behar and Netzer4, Reference Kaspi, Brandt, Netzer, George, Chartas, Behar, Sambruna, Garmire and Nousek5]. The lines of He-like ions are signs of presence of highly ionized plasmas, and they are useful to diagnose experimental and astrophysical plasma properties, such as electron density and temperature[Reference Ji, Schulz, Nowak, Marshall and Kallman1, Reference Jimenez-Garate, Hailey, den Herder, Zane and Ramsay3, Reference Gabriel and Jordan6–Reference Gabriel and Jordan8]. Therefore, modeling and analyzing these high-resolution spectra, accurate atomic data and spectroscopy interpretation for the K-shell lines are urgently needed.
Many theoretical calculations[Reference Behar and Netzer4, Reference Palmeri, Quinet, Mendoza, Bautista, Garcia, Witthoeft and Kallman9–Reference Wei, Shi, Wang, Zhong, Liang and Zhao11] have been performed to derive the wavelengths and transition rates of K-shell lines using kinds of atom structure codes. These include using HFR[Reference Cowan12] and AUTOSTRUCTURE[Reference Badnell13, Reference Eissner, Jones and Nussbaumer14] to calculate the wavelength and A-values of K-shell lines for some medium-Z elements. Their results agree well with the other previous works[Reference Behar and Netzer4, Reference Palmeri, Quinet, Mendoza, Bautista, Garcia, Witthoeft and Kallman9], but some disagreements still exist, for example, the difference from C-like ions radiative rates can be 40%[Reference Palmeri, Quinet, Mendoza, Bautista, Garcia, Witthoeft and Kallman9, Reference Wei, Shi, Wang, Zhong, Liang and Zhao11, Reference Chen, Reed, McWilliams, Guo, Barlow, Lee and Walker15]. In order to benchmark and testify the theoretical results, some experiments were carried out to measure the wavelengths of K-shell lines. Refs. [Reference Trabert and Fawcett16, Reference Trabert, Fawcett and Silver17] measured and identified K-shell lines in X-ray spectrum of foil-excited silicon. These lines were proved to be emitted by K-shell transitions in Si VIII–XIII, as well as by two electron one photon transitions. Ref. [Reference Mosnier, Barchewitz, Senemaud, Cukier and Dei-Cas18] reported
![]() $2p\rightarrow 1s$
transition lines in Si XI to Si XIV ions in beam-foil experiment. Ref. [Reference Faenov, Pikuz and Shlyaptseva19] measured satellites lines of Be-like through F-like ions for
$2p\rightarrow 1s$
transition lines in Si XI to Si XIV ions in beam-foil experiment. Ref. [Reference Faenov, Pikuz and Shlyaptseva19] measured satellites lines of Be-like through F-like ions for
![]() $Z=12{-}16$
elements in laser plasmas produced by a CO
$Z=12{-}16$
elements in laser plasmas produced by a CO
![]() $_{2}$
-laser. Ref. [Reference Hell, Miškovičová, Brown, Wilms, Clementson, Hanke, Beiersdorfer, Liedahl, Pottschmidt, Porter, Kilbourne, Kelley, Nowak and Schulz20] measured
$_{2}$
-laser. Ref. [Reference Hell, Miškovičová, Brown, Wilms, Clementson, Hanke, Beiersdorfer, Liedahl, Pottschmidt, Porter, Kilbourne, Kelley, Nowak and Schulz20] measured
![]() $\text{K}\unicode[STIX]{x1D6FC}$
transitions of silicon ions using EBIT-I electron beam ion trap at the Lawrence Livermore National Laboratory.
$\text{K}\unicode[STIX]{x1D6FC}$
transitions of silicon ions using EBIT-I electron beam ion trap at the Lawrence Livermore National Laboratory.
Few of the former works interpreted the line emission mechanism in detail. More importantly, we find that satellite lines may be blended with the He-like triplet lines, and impact their line ratios, which are widely used in plasma diagnosis. Here, we report the spectroscopic experiment of silicon on Shenguang II laser facility and the recalculated line ratios of He-like triplet. Section 2 is the experimental setups and calibrated spectra. Theoretical simulations and discussions about line emission mechanism are presented in Section 3. Section 4 presents the influence of satellite lines on the line ratios of He-like triplet, and the application to diagnose electron density and temperature is also discussed. Conclusion is in Section 5.
2 Experimental setups and spectra
The experiments were carried out on the Shenguang II laser facility at Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences. Two types of targets were performed to get the spectra of highly charged silicon ions. Figure 1(a) shows the Type I target, and the main part is a silicon plate with
![]() $400~\unicode[STIX]{x03BC}\text{m}$
in diameter. Shot 24 and Shot 26 used the Type I target. Figure 1(b) shows the Type II target and the schematic diagram of the experimental setups. In Type II target, a CH foil perpendicular to the silicon plate was added to the Type I target, which was used to obstruct the plasma evolution. Shot 28 and Shot 32 used the Type II target. In both types of shots, the center of the silicon plate lower surface was set at the target chamber center (TCC), and two 240 J driven laser beams were used, whose wavelengths were 351 nm and durations were 1 ns. The diameters of the focal spots were about
$400~\unicode[STIX]{x03BC}\text{m}$
in diameter. Shot 24 and Shot 26 used the Type I target. Figure 1(b) shows the Type II target and the schematic diagram of the experimental setups. In Type II target, a CH foil perpendicular to the silicon plate was added to the Type I target, which was used to obstruct the plasma evolution. Shot 28 and Shot 32 used the Type II target. In both types of shots, the center of the silicon plate lower surface was set at the target chamber center (TCC), and two 240 J driven laser beams were used, whose wavelengths were 351 nm and durations were 1 ns. The diameters of the focal spots were about
![]() $150~\unicode[STIX]{x03BC}\text{m}$
full-width at half-maximum (FWHM), and the incident laser intensity is about
$150~\unicode[STIX]{x03BC}\text{m}$
full-width at half-maximum (FWHM), and the incident laser intensity is about
![]() $2.4\times 10^{15}~\text{W}\cdot \text{cm}^{-2}$
[Reference Yuan, Wu, Li, Lu, Zhang, Yin, Su, Liao, Wei, Zhang, Han, Wang, Jiang, Du, Ding, Zhu, He, Zhao and Zhang21]. A crystal spectrometer[Reference Dong, Wang, Lu, Huang, Yuan, Liu, Lin, Li, Wei, Zhong, Shi, Jiang, Ding, Jiang, Du, He, Yu, Liu, Wang, Tang, Zhu, Zhao, Sheng and Zhang22] was used to record the spectrum of plasma. Additionally, another laser, whose wavelength was 527 nm and duration was 30 ps, was used as a probe. The profile of the plasmas was measured by a Nomarski interferometer, whose magnification factor was three[Reference Yuan, Wu, Li, Lu, Zhang, Yin, Su, Liao, Wei, Zhang, Han, Wang, Jiang, Du, Ding, Zhu, He, Zhao and Zhang21]. Both types of shots were repeated twice, and the repeatability is quite good. The experimental spectra are shown in Figures 2 and 3. However, the Type II spectra were impacted by some Cu lines, which were from the copper frame of the CH foil. We repeated the Type II target in 2017 with the beam energy raised to 250 J. The repeated Type II spectrum is shown in Figure 4. The slight differences in spectral intensities between the two shots of each type may result from laser energy deviation.
$2.4\times 10^{15}~\text{W}\cdot \text{cm}^{-2}$
[Reference Yuan, Wu, Li, Lu, Zhang, Yin, Su, Liao, Wei, Zhang, Han, Wang, Jiang, Du, Ding, Zhu, He, Zhao and Zhang21]. A crystal spectrometer[Reference Dong, Wang, Lu, Huang, Yuan, Liu, Lin, Li, Wei, Zhong, Shi, Jiang, Ding, Jiang, Du, He, Yu, Liu, Wang, Tang, Zhu, Zhao, Sheng and Zhang22] was used to record the spectrum of plasma. Additionally, another laser, whose wavelength was 527 nm and duration was 30 ps, was used as a probe. The profile of the plasmas was measured by a Nomarski interferometer, whose magnification factor was three[Reference Yuan, Wu, Li, Lu, Zhang, Yin, Su, Liao, Wei, Zhang, Han, Wang, Jiang, Du, Ding, Zhu, He, Zhao and Zhang21]. Both types of shots were repeated twice, and the repeatability is quite good. The experimental spectra are shown in Figures 2 and 3. However, the Type II spectra were impacted by some Cu lines, which were from the copper frame of the CH foil. We repeated the Type II target in 2017 with the beam energy raised to 250 J. The repeated Type II spectrum is shown in Figure 4. The slight differences in spectral intensities between the two shots of each type may result from laser energy deviation.

Figure 1. Two types of targets and schematic diagram of the experimental setups. (a) The Type I target. (b) The Type II shot and the schematic diagram of the experimental setups. The silicon plate is set at the target chamber center (TCC), and two driven laser beams are focused on it. A crystal spectrometer is used to record the spectrum of plasma.
Figures 5(a) and 5(b) are the interferograms of Type I and Type II shots with the probe beam delayed for 3 ns. This is obvious that the plasma of Type II shot has more complex construction than that of Type I shot. In other words, the CH foil impacted the evolution of the plasmas. Moreover, by Abel inversing the interferograms, the electron density distributions of the plasmas can be deduced, which are shown in Figures 2(c) and 2(d). The electron densities of the plasmas are generally above
![]() $10^{18}~\text{cm}^{-3}$
.
$10^{18}~\text{cm}^{-3}$
.
3 Theoretical simulations
We use the radiative-collisional code (RCF) based on flexible atomic code (FAC)[Reference Han, Wang, Salzmann and Zhao23] to simulate the experimental spectra. RCF is a code for steady-state plasmas, which is under nonlocal thermodynamic equilibrium condition. All the atomic data are calculated by the FAC[Reference Gu24] , which ensures calculating completeness and consistency of atomic data. Applied to some photoionization experiments, RCF well reproduces the charge state distribution of photoionizing Fe experiment, which was carried out by Foord et al. on Z-facility[Reference Han, Wang, Salzmann and Zhao23, Reference Foord, Heeter, van Hoof, Thoe, Bailey, Cuneo, Chung, Liedahl, Fournier, Chandler, Jonauskas, Mix, Ramsbottom, Springer, Keenan, Rose and Goldstein25, Reference Foord, Heeter, Chung, van Hoof, Bailey, Cuneo, Liedahl, Fournier, Jonauskas, Kisielius, Ramsbottom, Springer, Keenan, Rose and Goldstein26], and the emission spectrum of photoionizing Si experiment, which was achieved by Fujioka et al. on GEKKO-XII[Reference Fujioka, Takabe, Yamamoto, Salzmann, Wang, Nishimura, Li, Dong, Wang, Zhang, Rhee, Lee, Han, Tanabe, Fujiwara, Nakabayashi, Zhao, Zhang and Mima27, Reference Han, Wang, Liang and Zhao28].
The atomic data include ions from C-like to bare nuclei. The maximum of principle quantum number,
![]() $n_{\text{max}}$
, is limited to 4 for C-like, B-like and Be-like ions.
$n_{\text{max}}$
, is limited to 4 for C-like, B-like and Be-like ions.
![]() $n_{\text{max}}$
s of Li-like, He-like and H-like ions are 7. In the simulations, the plasmas are assumed to be in collisional radiative steady state. Collisional processes include collisional excitation, collisional ionization, autoionization and their inverse processes, which are collisional deexcitation, three-body recombination and dielectron capture. Radiative processes include radiative recombination and E1, E2, M1 and M2 types of radiative decays. The spectra we are interested in, are from the He-like and Li-like ions, which only exist in highly ionized plasma. Although the spectra might be influenced by lines from lower ionized ions, the comparison between the experimental and theoretical spectra shows that the influence is small, such as the tail of the second peaks in Figure 2. So we assume the plasmas are in steady state, which are highly ionized. In all the following RCF theoretical spectra, line intensities are convolved using Gaussian profile with an FWHM about 5 m Å (1 eV in energy).
$n_{\text{max}}$
s of Li-like, He-like and H-like ions are 7. In the simulations, the plasmas are assumed to be in collisional radiative steady state. Collisional processes include collisional excitation, collisional ionization, autoionization and their inverse processes, which are collisional deexcitation, three-body recombination and dielectron capture. Radiative processes include radiative recombination and E1, E2, M1 and M2 types of radiative decays. The spectra we are interested in, are from the He-like and Li-like ions, which only exist in highly ionized plasma. Although the spectra might be influenced by lines from lower ionized ions, the comparison between the experimental and theoretical spectra shows that the influence is small, such as the tail of the second peaks in Figure 2. So we assume the plasmas are in steady state, which are highly ionized. In all the following RCF theoretical spectra, line intensities are convolved using Gaussian profile with an FWHM about 5 m Å (1 eV in energy).

Figure 2. Black and gray lines are the experimental spectra of two Type I shots. Red line is the simulation results (Case A), where
![]() $n_{e}=10^{21}~\text{cm}^{-3}$
and
$n_{e}=10^{21}~\text{cm}^{-3}$
and
![]() $T_{e}=150~\text{eV}$
. Blue line is the unbroadened theoretical line.
$T_{e}=150~\text{eV}$
. Blue line is the unbroadened theoretical line.

Figure 3. Black and gray lines are the experimental spectra of two Type II shots. Red line is the simulation results (Case B), where
![]() $n_{e}=10^{18}~\text{cm}^{-3}$
and
$n_{e}=10^{18}~\text{cm}^{-3}$
and
![]() $T_{e}=300~\text{eV}$
.
$T_{e}=300~\text{eV}$
.

Figure 4. Black line is the experimental spectrum of repeated Type II targets in 2017. Red line is the simulation results (Case C), where
![]() $n_{e}=5\times 10^{18}~\text{cm}^{-3}$
and
$n_{e}=5\times 10^{18}~\text{cm}^{-3}$
and
![]() $T_{e}=250~\text{eV}$
.
$T_{e}=250~\text{eV}$
.

Figure 5. (a) and (b) are the interferograms of Type I and Type II shots. (c) and (d) are the electron density distribution deduced by Abel inversing of (a) and (b).
Table 1. Experimental peak centroids with statistical errors of Shot 26, and the present and theoretical wavelength of intense lines in Case A.

Figures 2–4 show the simulation results. Case A, where the electron density is
![]() $10^{21}~\text{cm}^{-3}$
and the electron temperature is 150 eV, well reproduces the two stocky peaks in the Type I spectra. The tail of the second peak in long wavelength range may attribute to the lines of Be-like and B-like ions, which are emitted in low temperature condition. In Case B, most of the peaks in Type II spectrum are reproduced, and the input parameters are
$10^{21}~\text{cm}^{-3}$
and the electron temperature is 150 eV, well reproduces the two stocky peaks in the Type I spectra. The tail of the second peak in long wavelength range may attribute to the lines of Be-like and B-like ions, which are emitted in low temperature condition. In Case B, most of the peaks in Type II spectrum are reproduced, and the input parameters are
![]() $n_{e}=10^{18}~\text{cm}^{-3}$
and
$n_{e}=10^{18}~\text{cm}^{-3}$
and
![]() $T_{e}=300~\text{eV}$
. The unproduced peaks may be Cu L-shell lines, which are emitted by the copper frame of the CH foil[Reference Comet, Pain, Gilleron, Piron, Denis-Petit, Meot, Gosselin, Morel, Hannachi, Gobet, Tarisien and Versteegen29]. Figure 4 shows the Si spectrum without Cu lines, and Case C gets a better result than Case B. The big differences of the two groups of input parameters indicate that the CH foil impacted the evolution of the plasma in Type II shots. It seems that the low density and high temperature part of plasma expanded and dissipated quickly in the Type I shot. Then, the spectrum of the high density but low temperature part was recorded. While in the Type II shots, the low density part was reflected by the CH foil, diluting the high density part. The accurate evolution needs hydrodynamic simulation, but we only talk about the spectrum emission in the present paper. The intense lines in these two cases are listed in Tables 1 and 2. In addition, the available wavelength results of Palmeri et al.
[Reference Palmeri, Quinet, Mendoza, Bautista, Garcia, Witthoeft and Kallman9] are also listed in Tables 1 and 2 as comparison. Two groups of data are in good agreement, and the difference of most of the lines is less than 0.01 Å.
$T_{e}=300~\text{eV}$
. The unproduced peaks may be Cu L-shell lines, which are emitted by the copper frame of the CH foil[Reference Comet, Pain, Gilleron, Piron, Denis-Petit, Meot, Gosselin, Morel, Hannachi, Gobet, Tarisien and Versteegen29]. Figure 4 shows the Si spectrum without Cu lines, and Case C gets a better result than Case B. The big differences of the two groups of input parameters indicate that the CH foil impacted the evolution of the plasma in Type II shots. It seems that the low density and high temperature part of plasma expanded and dissipated quickly in the Type I shot. Then, the spectrum of the high density but low temperature part was recorded. While in the Type II shots, the low density part was reflected by the CH foil, diluting the high density part. The accurate evolution needs hydrodynamic simulation, but we only talk about the spectrum emission in the present paper. The intense lines in these two cases are listed in Tables 1 and 2. In addition, the available wavelength results of Palmeri et al.
[Reference Palmeri, Quinet, Mendoza, Bautista, Garcia, Witthoeft and Kallman9] are also listed in Tables 1 and 2 as comparison. Two groups of data are in good agreement, and the difference of most of the lines is less than 0.01 Å.
Table 2. Experimental peak centroids with statistical errors from 6.6 Å to 6.85 Å of Shot 32 and the present and theoretical wavelength of intense lines in Case B.
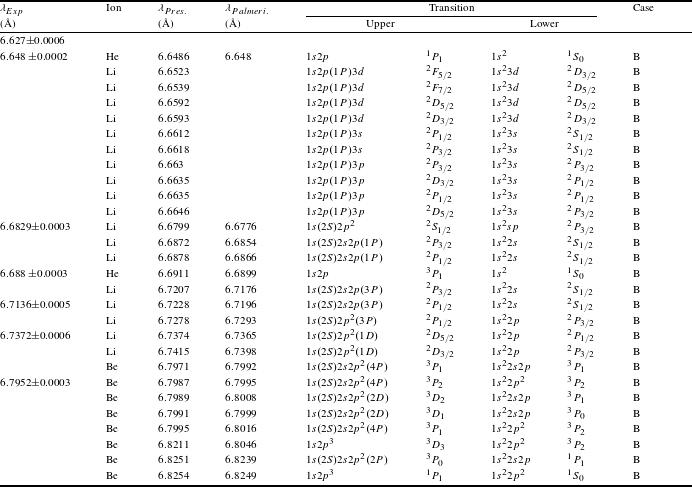
In Case A, each of the two stocky peaks is not formed by single transition, but forest of lines, as shown by the theoretical unbroadened lines in Figure 3. As Figure 3 and Table 1 show, the resonance line (
![]() $r$
or
$r$
or
![]() $w/1s^{2}$
$w/1s^{2}$
![]() $^{1}S_{0}$
–
$^{1}S_{0}$
–
![]() $1s2p$
$1s2p$
![]() $^{1}P_{1}$
, 6.648 Å) contributes most of the intensity of the left peak. The rest part of the two peaks are constructed by transitions from
$^{1}P_{1}$
, 6.648 Å) contributes most of the intensity of the left peak. The rest part of the two peaks are constructed by transitions from
![]() $1s2l2l^{\prime }$
to
$1s2l2l^{\prime }$
to
![]() $1s^{2}2l$
, from
$1s^{2}2l$
, from
![]() $1s2l3l^{\prime }$
to
$1s2l3l^{\prime }$
to
![]() $1s^{2}3l^{\prime }$
and even from
$1s^{2}3l^{\prime }$
and even from
![]() $1s2l4l^{\prime }$
to
$1s2l4l^{\prime }$
to
![]() $1s^{2}4l^{\prime }$
. Because these lines are surrounded with the He-
$1s^{2}4l^{\prime }$
. Because these lines are surrounded with the He-
![]() $\unicode[STIX]{x1D6FC}$
lines, they are called satellite lines of the He-
$\unicode[STIX]{x1D6FC}$
lines, they are called satellite lines of the He-
![]() $\unicode[STIX]{x1D6FC}$
lines. These lines not only huddle together, but also have similar intensities. Even though they are only convolved with an FWHM of 5 m Å, they are indistinguishable. As a result, two stocky peaks are formed, and the Gaussian centroids of the peaks shift a little from the strongest lines. In other words, the satellite lines blend with the He-like lines and affect the line strengths significantly. In Case B, there are also many Li-like lines, but the number of intense lines decreases and their relative intensities are large, so that the peaks become slightly thinner and more distinguishable than Case A.
$\unicode[STIX]{x1D6FC}$
lines. These lines not only huddle together, but also have similar intensities. Even though they are only convolved with an FWHM of 5 m Å, they are indistinguishable. As a result, two stocky peaks are formed, and the Gaussian centroids of the peaks shift a little from the strongest lines. In other words, the satellite lines blend with the He-like lines and affect the line strengths significantly. In Case B, there are also many Li-like lines, but the number of intense lines decreases and their relative intensities are large, so that the peaks become slightly thinner and more distinguishable than Case A.
In the two cases, the He-like ion has a fraction of 96% and 87%, respectively. The energy gaps between the
![]() $1s2l$
levels and ground state are larger than 1800 eV. While the electron temperature is several hundreds of eV in the two cases, most of the He-like ions are frozen at the ground state. The fraction of Li-like ion and H-like ion is much smaller than that of He-like ion, so that neither ionization nor recombination processes can populate the resonance line efficiently. Thus, the resonance line is mainly populated by collisional excitation from the tremendous amount of the ground state of He-like ion. Combing with large radiative decay rate, which is
$1s2l$
levels and ground state are larger than 1800 eV. While the electron temperature is several hundreds of eV in the two cases, most of the He-like ions are frozen at the ground state. The fraction of Li-like ion and H-like ion is much smaller than that of He-like ion, so that neither ionization nor recombination processes can populate the resonance line efficiently. Thus, the resonance line is mainly populated by collisional excitation from the tremendous amount of the ground state of He-like ion. Combing with large radiative decay rate, which is
![]() $3.87\times 10^{13}~\text{s}^{-1}$
, the resonance line is the strongest line.
$3.87\times 10^{13}~\text{s}^{-1}$
, the resonance line is the strongest line.
Under such conditions, where temperatures are hundreds of eV, the Li-like ion is easier to be ionized than to be excited by collision, so that the Li-like ion has small populations. However, Li-like lines strongly affect the spectrum profile in the two cases. The reason is that these Li-like lines are populated by dielectronic capture from the ground state of He-like ion, and they also have comparable radiative decay rates with the resonance line. There are two main processes to produce Li-like ions with K-shell vacancies in a collision-dominating plasma, i.e., collisional excitation and dielectronic capture. Because of the small population of Li-like ion, the contribution of collisional excitation is negligible. The Li-like levels, which have K-shell vacancies, usually have large autoionization rates to the ground state of He-like ion. Therefore, dielectron capture, which is the reverse process of autoionization, has large reaction rate while the ground state of He-like ion has tremendous amount. Moreover, the doubly excited Li-like lines usually have comparable radiative decay rates with the resonance line. For example, the radiative decay rate of
![]() $1s^{2}2s$
$1s^{2}2s$
![]() $^{2}S_{1/2}$
to
$^{2}S_{1/2}$
to
![]() $1s2s2p$
$1s2s2p$
![]() $^{2}P_{1/2}$
is
$^{2}P_{1/2}$
is
![]() $3.26\times 10^{13}~\text{s}^{-1}$
. As a result, forest of intense Li-like lines are produced.
$3.26\times 10^{13}~\text{s}^{-1}$
. As a result, forest of intense Li-like lines are produced.
However, comparing with those above lines, the intercombination line (
![]() $i$
or
$i$
or
![]() $x/1s^{2}$
$x/1s^{2}$
![]() $^{1}S_{0}$
–
$^{1}S_{0}$
–
![]() $1s2p$
$1s2p$
![]() $^{3}P_{2}$
and
$^{3}P_{2}$
and
![]() $y/1s^{2}$
$y/1s^{2}$
![]() $^{1}S_{0}$
–
$^{1}S_{0}$
–
![]() $1s2p$
$1s2p$
![]() $^{3}P_{1}$
, 6.688 Å) and the forbidden line (
$^{3}P_{1}$
, 6.688 Å) and the forbidden line (
![]() $f$
or
$f$
or
![]() $z/1s^{2}$
$z/1s^{2}$
![]() $^{1}S_{0}$
–
$^{1}S_{0}$
–
![]() $1s2s$
$1s2s$
![]() $^{3}S_{1}$
, 6.74 Å) are weaker. The reason is that the radiative decay rates of these two lines are too small. The A-value of intercombination is
$^{3}S_{1}$
, 6.74 Å) are weaker. The reason is that the radiative decay rates of these two lines are too small. The A-value of intercombination is
![]() $1.36\times 10^{11}~\text{s}^{-1}$
and
$1.36\times 10^{11}~\text{s}^{-1}$
and
![]() $3.27\times 10^{5}~\text{s}^{-1}$
for the forbidden lines, which are several orders of magnitude smaller than those intense lines. When there are no other processes to make up this huge disadvantage, the intercombination and forbidden lines are drawn in the Li-like lines.
$3.27\times 10^{5}~\text{s}^{-1}$
for the forbidden lines, which are several orders of magnitude smaller than those intense lines. When there are no other processes to make up this huge disadvantage, the intercombination and forbidden lines are drawn in the Li-like lines.
4 Developed
 $G$
value and
$G$
value and
 $R$
value
$R$
value
The line
![]() $G$
value
$G$
value
![]() $(G=(f+i)/r)$
and
$(G=(f+i)/r)$
and
![]() $R$
value
$R$
value
![]() $(R=f/i)$
of He-
$(R=f/i)$
of He-
![]() $\unicode[STIX]{x1D6FC}$
lines are widely used in experimental and astrophysical plasma diagnosis[Reference Gabriel and Jordan6–Reference Gabriel and Jordan8]. Some previous works[Reference Porquet, Mewe, Dubau, Raassen and Kaastra30–Reference Sylwester, Sylwester and Phillips32] also reported that in some low-resolution spectra the satellite lines blend with the He-like lines, which is consistent with the present results. We have discussed the influence of satellite lines on these line ratios for photoionized plasmas, and they impact the diagnosing result significantly[Reference Wang, Han, Salzmann and Zhao33]. In this section, combining with the present experimental results, we discuss the influences of satellite lines on these two line ratios for the collision-dominating plasmas.
$\unicode[STIX]{x1D6FC}$
lines are widely used in experimental and astrophysical plasma diagnosis[Reference Gabriel and Jordan6–Reference Gabriel and Jordan8]. Some previous works[Reference Porquet, Mewe, Dubau, Raassen and Kaastra30–Reference Sylwester, Sylwester and Phillips32] also reported that in some low-resolution spectra the satellite lines blend with the He-like lines, which is consistent with the present results. We have discussed the influence of satellite lines on these line ratios for photoionized plasmas, and they impact the diagnosing result significantly[Reference Wang, Han, Salzmann and Zhao33]. In this section, combining with the present experimental results, we discuss the influences of satellite lines on these two line ratios for the collision-dominating plasmas.
In the present experimental spectra, the intercombination and forbidden lines are weaker than the Li-like lines, and their positions are occupied by many Li-like lines. It is hard to distinguish these lines clearly and to measure their strengths accurately, and calculations of the line ratios are impossible. So we develop the identification of the
![]() $G$
value and
$G$
value and
![]() $R$
value, where the contributions of the blending satellite lines are taken into the line intensities. For simplicity, one can think that the three peaks in Figure 4 are the extended resonance, intercombination and forbidden lines, respectively. The developed line ratios are called as
$R$
value, where the contributions of the blending satellite lines are taken into the line intensities. For simplicity, one can think that the three peaks in Figure 4 are the extended resonance, intercombination and forbidden lines, respectively. The developed line ratios are called as
![]() $G+$
value and
$G+$
value and
![]() $R+$
value[Reference Wang, Han, Salzmann and Zhao33]. The trends of
$R+$
value[Reference Wang, Han, Salzmann and Zhao33]. The trends of
![]() $G$
and
$G$
and
![]() $G+$
along with electron temperature are plotted in Figure 6, and the trends of
$G+$
along with electron temperature are plotted in Figure 6, and the trends of
![]() $R$
and
$R$
and
![]() $R+$
along with electron density are plotted in Figure 7. If the plasma is lowly ionized, there will be no intense Li-like and He-like lines, and the discussions about these two ratios are meaningless. The plotted line ratios are calculated in cases with average ionizations larger than 10.
$R+$
along with electron density are plotted in Figure 7. If the plasma is lowly ionized, there will be no intense Li-like and He-like lines, and the discussions about these two ratios are meaningless. The plotted line ratios are calculated in cases with average ionizations larger than 10.

Figure 6. The
![]() $G+$
and
$G+$
and
![]() $G$
values. Every line has same electron density, which spans from
$G$
values. Every line has same electron density, which spans from
![]() $10^{17}~\text{cm}^{-3}$
to
$10^{17}~\text{cm}^{-3}$
to
![]() $10^{22}~\text{cm}^{-3}$
exponentially, and the line ratios are plotted as a function of electron temperature.
$10^{22}~\text{cm}^{-3}$
exponentially, and the line ratios are plotted as a function of electron temperature.

Figure 7. The
![]() $R+$
(red) and
$R+$
(red) and
![]() $R$
(black) values. Every line has same electron temperature, which spans from 100 eV to 500 eV incrementally, and the line ratios are plotted as a function of electron density.
$R$
(black) values. Every line has same electron temperature, which spans from 100 eV to 500 eV incrementally, and the line ratios are plotted as a function of electron density.
As mentioned above, the intercombination and forbidden lines are much weaker than the resonance line, so that the
![]() $G$
value is always very small. In Figure 6, the
$G$
value is always very small. In Figure 6, the
![]() $G$
value is insensitive to electron temperature. The reason is that the energy gap between the resonance line and the forbidden line is about 25 eV, but the temperature in calculation is hundreds of eV. Therefore, the
$G$
value is insensitive to electron temperature. The reason is that the energy gap between the resonance line and the forbidden line is about 25 eV, but the temperature in calculation is hundreds of eV. Therefore, the
![]() $G$
value is not obviously influenced by the temperature in this range. The changing of the input parameter is along with changing of ionization degree. When temperature rises, the fraction of Li-like ion decreases and He-like ion increases. The intensities of the lines change with the ions. We also know that the satellite lines enter the peaks a lot, which are at the position of the intercombination and forbidden lines. In consequence,
$G$
value is not obviously influenced by the temperature in this range. The changing of the input parameter is along with changing of ionization degree. When temperature rises, the fraction of Li-like ion decreases and He-like ion increases. The intensities of the lines change with the ions. We also know that the satellite lines enter the peaks a lot, which are at the position of the intercombination and forbidden lines. In consequence,
![]() $G+$
is quite large in the low temperature range, and decreases as the temperature rises. With same temperature, the low density case has lower ionization degree than the higher one. Thus, the
$G+$
is quite large in the low temperature range, and decreases as the temperature rises. With same temperature, the low density case has lower ionization degree than the higher one. Thus, the
![]() $G+$
value of the lower density case is larger than that of the higher density case. When ionization degree is high enough, the influence of satellite lines is not important any more, and the
$G+$
value of the lower density case is larger than that of the higher density case. When ionization degree is high enough, the influence of satellite lines is not important any more, and the
![]() $G+$
value converges to the
$G+$
value converges to the
![]() $G$
value.
$G$
value.
The energy gap between the intercombination line and forbidden line is about 15 eV, so that electron temperature and density rarely impact the
![]() $R$
value. When the influence of satellite line is concerned, the intensity of the peaks shifts to shorter wavelength range as the ionization degree increases. With same density, the intensity at the lower temperature is larger than in the higher temperature case.
$R$
value. When the influence of satellite line is concerned, the intensity of the peaks shifts to shorter wavelength range as the ionization degree increases. With same density, the intensity at the lower temperature is larger than in the higher temperature case.

Figure 8. The solid scatters are the experimental
![]() $R$
and
$R$
and
![]() $G$
values. The open scatters are the
$G$
values. The open scatters are the
![]() $R+$
and
$R+$
and
![]() $G+$
values of the three theoretical cases.
$G+$
values of the three theoretical cases.
Figure 8 shows the comparison of the experimental and theoretical
![]() $R$
and
$R$
and
![]() $G$
values. Cases A and C cooperate with the experiment very well. The difference in Case B is because of the influence of the Cu lines, which enhance the intensities of intercombination and forbidden lines and result in larger
$G$
values. Cases A and C cooperate with the experiment very well. The difference in Case B is because of the influence of the Cu lines, which enhance the intensities of intercombination and forbidden lines and result in larger
![]() $G$
values than Case B.
$G$
values than Case B.
When used to diagnose the electron temperature and density of plasma, the traditional
![]() $G$
value and
$G$
value and
![]() $R$
value are used separately[Reference Porquet and Dubau7]. Few of the former works discussed the influence of ionization degree on these two ratios. In Ref. [Reference Porquet and Dubau7],
$R$
value are used separately[Reference Porquet and Dubau7]. Few of the former works discussed the influence of ionization degree on these two ratios. In Ref. [Reference Porquet and Dubau7],
![]() $G$
value and
$G$
value and
![]() $R$
value are believed to be independent in some range, but they are sensitive to a parameter
$R$
value are believed to be independent in some range, but they are sensitive to a parameter
![]() $\text{H}\text{-}\text{like}/\text{He}\text{-}\text{like}$
, which is determined by electron temperature and density simultaneously. In the present work, the
$\text{H}\text{-}\text{like}/\text{He}\text{-}\text{like}$
, which is determined by electron temperature and density simultaneously. In the present work, the
![]() $G+$
and
$G+$
and
![]() $R+$
are sensitive to both electron temperature and density in the given ranges. We think this is more reasonable in diagnosing the plasma, and the electron temperature and density should be determined by the two ratios collectively.
$R+$
are sensitive to both electron temperature and density in the given ranges. We think this is more reasonable in diagnosing the plasma, and the electron temperature and density should be determined by the two ratios collectively.
5 Conclusion
Two kinds of shots were performed on Shenguang II laser facility to study the spectroscopy of silicon plasmas under different plasma conditions. The spectra of two types of shots are different, which reveals that the vertical CH foil in the Type II target impacted the evolution of the plasma. X-ray spectra spanning from 6.6 Å to 6.85 Å of collisional silicon plasmas have been recorded with crystal spectrometer. With the radiative-collisional codes[Reference Han, Wang, Salzmann and Zhao23], we simulate the spectra of Shot 26 and Shot 32, and successfully reproduce most of the prominent peaks in the range of 6.6–6.85 Å. The line wavelengths between the present result and the result in Ref. [Reference Palmeri, Quinet, Mendoza, Bautista, Garcia, Witthoeft and Kallman9] agree within 0.01 Å. According to the simulation results, collisional excitation produces strong He-like resonance line, and dielectronic capture produces plenty of satellite lines. The spectra of He-like ion triplet lines in 6.64–6.75 Å are strongly influenced by the satellite lines, even in He-like ion dominating conditions. The traditional
![]() $G$
value and
$G$
value and
![]() $R$
value are insensitive to electron temperature and density, and they cannot be used in the diagnosing of electron temperature and density of plasma. We develop the identification of
$R$
value are insensitive to electron temperature and density, and they cannot be used in the diagnosing of electron temperature and density of plasma. We develop the identification of
![]() $G$
value and
$G$
value and
![]() $R$
value, where the influence of the satellite lines is taken into the calculations of the line ratios. The developed line ratios,
$R$
value, where the influence of the satellite lines is taken into the calculations of the line ratios. The developed line ratios,
![]() $G+$
and
$G+$
and
![]() $R+$
, are influenced by the electron temperature and density, and they can be used in plasma diagnosing in some degree.
$R+$
, are influenced by the electron temperature and density, and they can be used in plasma diagnosing in some degree.
Acknowledgements
This work was supported by the Science Challenge Project (No. TZ2016005), the National Basic Research Program of China (No. 2013CBA01503), the National Natural Science Foundation of China (Nos. 10905004, 11220101002, and 11622323), and the Fundamental Research Funds for the Central Universities.