1 Introduction
Blazar jets are beam-like linear features observable over a broad range of frequencies and generated perpendicularly to the accretion disc of super massive black holes[Reference Meier, Koide and Uchida1, Reference Nemmen, Georganopoulos, Guiriec, Meyer, Gehrels and Sambruna2]. They normally extend over intergalactic distances (many thousands of light years) and are observed to generate highly non-thermal radio emission at frequencies ranging from a few to 100s of GHz, with intrinsic brightness temperatures in excess of
![]() $10^{14}~\text{K}$
[Reference Begelman, Ergun and Rees3]. Begelman et al. suggested[Reference Begelman, Ergun and Rees3] that a cyclotron-maser instability is responsible for the generation of these emissions in the low density (
$10^{14}~\text{K}$
[Reference Begelman, Ergun and Rees3]. Begelman et al. suggested[Reference Begelman, Ergun and Rees3] that a cyclotron-maser instability is responsible for the generation of these emissions in the low density (
![]() $\unicode[STIX]{x1D714}_{ce}>\unicode[STIX]{x1D714}_{pe}$
), magnetized plasma of the jet[Reference Begelman, Ergun and Rees3–Reference Treumann5], where
$\unicode[STIX]{x1D714}_{ce}>\unicode[STIX]{x1D714}_{pe}$
), magnetized plasma of the jet[Reference Begelman, Ergun and Rees3–Reference Treumann5], where
![]() $\unicode[STIX]{x1D714}_{ce}$
and
$\unicode[STIX]{x1D714}_{ce}$
and
![]() $\unicode[STIX]{x1D714}_{pe}$
are the electron-cyclotron and plasma frequencies, respectively. It is assumed that within the jet, small scale magnetic mirrors/convergent flux tubes may be formed via shocks or hydrodynamic instabilities, providing the environment for generating the required electron velocity distribution[Reference Begelman, Ergun and Rees3, Reference Bingham, Kellett, Cairns, Tonge and Mendonca4].
$\unicode[STIX]{x1D714}_{pe}$
are the electron-cyclotron and plasma frequencies, respectively. It is assumed that within the jet, small scale magnetic mirrors/convergent flux tubes may be formed via shocks or hydrodynamic instabilities, providing the environment for generating the required electron velocity distribution[Reference Begelman, Ergun and Rees3, Reference Bingham, Kellett, Cairns, Tonge and Mendonca4].
The background magnetic field within a blazar jet is assumed to be very high[Reference O’Sullivan and Gabuzda6] leading to large electron cyclotron frequencies for the energetic electron population within the jet in the 1–100 GHz range. This results in
![]() $\unicode[STIX]{x1D714}_{ce}\gg \unicode[STIX]{x1D714}_{pe}$
[Reference Begelman, Ergun and Rees3], a necessary condition for the cyclotron-maser instability. Begelman, Ergun and Rees[Reference Begelman, Ergun and Rees3] deduced values for the ratio of cyclotron frequency to plasma frequency that indicate the efficiency of the maser-emission process for blazar jets could be an order of magnitude greater than for the auroral maser-emission process. Gurnett estimated the conversion efficiency from electron beam to electromagnetic (EM) radiation to be about 1% in the auroral zone[Reference Gurnett7]. Begelmann, Ergun and Rees[Reference Begelman, Ergun and Rees3] concluded that the radiation could indeed be due to the cyclotron-maser instability driven by an electron horseshoe/ring distribution. In previous work it has been shown that a suitable ring-type velocity distribution may be generated directly via the surfatron mechanism, through energization of particles perpendicular to the magnetostatic field[Reference Katsouleas and Dawson8]. We have also proposed an alternative scheme by which electrons may be accelerated and magnetically compressed within a magnetised collisionless shock, resulting in a suitable horseshoe or crescent-type velocity distribution[Reference Bingham, Kellett, Cairns, Tonge and Mendonca4]. Both mechanisms are viable within the turbulent, highly magnetised plasma of a blazar jet, with field-aligned currents and small scale magnetic mirrors expected to be observed in association with quasi-perpendicular collisionless shocks[Reference Begelman, Ergun and Rees3]. Counter-streaming ion populations formed at such shocks can excite lower hybrid waves via the modified two-stream instability[Reference McBride, Ott, Boris and Orens9, Reference Yamada and Owens10]. These waves are capable of accelerating electrons parallel to the magnetic field and up to high energies[Reference McClements, Bingham, Su, Dawson and Spicer11–Reference Vink and Laming13]. The resultant energetic electron tail distributions can then experience magnetic compression when moving from the upstream to downstream region of the magnetised collisionless shock, producing a horseshoe or crescent-type distribution function which is unstable to the cyclotron-maser instability. This model[Reference Shapiro and Shevchenko14] has been used to account for acceleration of energetic particles at comets[Reference Bingham, Dawson, Shapiro, Mendis and Kellett15] and within supernova remnants[Reference Bingham, Kellett, Dawson, Shapiro and Mendis16, Reference Bingham, Kellett, Bryans, Summers, Torney, Shapiro, Spicer and O’Brien17]. The same model has also been applied successfully to explain energetic particles in artificial releases from spacecraft[Reference Bingham, Shapiro, Tsytovich, de Angelis, Gilman and Shevchenko18] and the physics of collisionless shocks near lunar magnetic abnormalities[Reference Bamford, Kellett, Bradford, Norberg, Thornton, Gibson, Crawford, Silva, Gargat é and Bingham19, Reference Bamford, Alves, Cruz, Kellett, Fonseca, O Silva, Trines, Halekas, Kramer and Harnett20] and in the globally induced lunar magnetosphere[Reference Bingham, Bamford, Kellett and Shapiro21]. Recently, this model has been tested in a laser-plasma experiment[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22] and successfully modelled by using PIC (particle-in-cell) codes[Reference Cruz, Alves, Bamford, Bingham, Fonseca and Silva23]. The escape of cyclotron-maser radiation from a blazar jet has been previously considered in some detail[Reference Begelman, Ergun and Rees3, Reference Treumann5], with various factors debated including second harmonic cyclotron absorption and synchrotron absorption. Both mechanisms are potentially the most significant impediments, but can be suitably accounted for[Reference Begelman, Ergun and Rees3] in the case of a blazar jet. Within the turbulent magnetised plasma of a jet, the second harmonic absorption layer is considered to occur perpendicularly to the magnetostatic field[Reference Begelman, Ergun and Rees3], with the generated X-mode radiation also propagating radially outwards, almost perpendicularly to the magnetic field. It was shown by Begelman et al. that the thickness of the second harmonic layer can be approximated as
$\unicode[STIX]{x1D714}_{ce}\gg \unicode[STIX]{x1D714}_{pe}$
[Reference Begelman, Ergun and Rees3], a necessary condition for the cyclotron-maser instability. Begelman, Ergun and Rees[Reference Begelman, Ergun and Rees3] deduced values for the ratio of cyclotron frequency to plasma frequency that indicate the efficiency of the maser-emission process for blazar jets could be an order of magnitude greater than for the auroral maser-emission process. Gurnett estimated the conversion efficiency from electron beam to electromagnetic (EM) radiation to be about 1% in the auroral zone[Reference Gurnett7]. Begelmann, Ergun and Rees[Reference Begelman, Ergun and Rees3] concluded that the radiation could indeed be due to the cyclotron-maser instability driven by an electron horseshoe/ring distribution. In previous work it has been shown that a suitable ring-type velocity distribution may be generated directly via the surfatron mechanism, through energization of particles perpendicular to the magnetostatic field[Reference Katsouleas and Dawson8]. We have also proposed an alternative scheme by which electrons may be accelerated and magnetically compressed within a magnetised collisionless shock, resulting in a suitable horseshoe or crescent-type velocity distribution[Reference Bingham, Kellett, Cairns, Tonge and Mendonca4]. Both mechanisms are viable within the turbulent, highly magnetised plasma of a blazar jet, with field-aligned currents and small scale magnetic mirrors expected to be observed in association with quasi-perpendicular collisionless shocks[Reference Begelman, Ergun and Rees3]. Counter-streaming ion populations formed at such shocks can excite lower hybrid waves via the modified two-stream instability[Reference McBride, Ott, Boris and Orens9, Reference Yamada and Owens10]. These waves are capable of accelerating electrons parallel to the magnetic field and up to high energies[Reference McClements, Bingham, Su, Dawson and Spicer11–Reference Vink and Laming13]. The resultant energetic electron tail distributions can then experience magnetic compression when moving from the upstream to downstream region of the magnetised collisionless shock, producing a horseshoe or crescent-type distribution function which is unstable to the cyclotron-maser instability. This model[Reference Shapiro and Shevchenko14] has been used to account for acceleration of energetic particles at comets[Reference Bingham, Dawson, Shapiro, Mendis and Kellett15] and within supernova remnants[Reference Bingham, Kellett, Dawson, Shapiro and Mendis16, Reference Bingham, Kellett, Bryans, Summers, Torney, Shapiro, Spicer and O’Brien17]. The same model has also been applied successfully to explain energetic particles in artificial releases from spacecraft[Reference Bingham, Shapiro, Tsytovich, de Angelis, Gilman and Shevchenko18] and the physics of collisionless shocks near lunar magnetic abnormalities[Reference Bamford, Kellett, Bradford, Norberg, Thornton, Gibson, Crawford, Silva, Gargat é and Bingham19, Reference Bamford, Alves, Cruz, Kellett, Fonseca, O Silva, Trines, Halekas, Kramer and Harnett20] and in the globally induced lunar magnetosphere[Reference Bingham, Bamford, Kellett and Shapiro21]. Recently, this model has been tested in a laser-plasma experiment[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22] and successfully modelled by using PIC (particle-in-cell) codes[Reference Cruz, Alves, Bamford, Bingham, Fonseca and Silva23]. The escape of cyclotron-maser radiation from a blazar jet has been previously considered in some detail[Reference Begelman, Ergun and Rees3, Reference Treumann5], with various factors debated including second harmonic cyclotron absorption and synchrotron absorption. Both mechanisms are potentially the most significant impediments, but can be suitably accounted for[Reference Begelman, Ergun and Rees3] in the case of a blazar jet. Within the turbulent magnetised plasma of a jet, the second harmonic absorption layer is considered to occur perpendicularly to the magnetostatic field[Reference Begelman, Ergun and Rees3], with the generated X-mode radiation also propagating radially outwards, almost perpendicularly to the magnetic field. It was shown by Begelman et al. that the thickness of the second harmonic layer can be approximated as
![]() ${\sim}r_{m}\unicode[STIX]{x1D714}_{pe}/\unicode[STIX]{x1D714}_{ce}$
which is relatively thin and results in attenuation of 10%, where
${\sim}r_{m}\unicode[STIX]{x1D714}_{pe}/\unicode[STIX]{x1D714}_{ce}$
which is relatively thin and results in attenuation of 10%, where
![]() $r_{m}$
is the radius of the jet at the emission region. Another consideration is the potential for refraction of the generated radiation due to the gradient in plasma density associated with the quasi-perpendicular shock. From our previous consideration for the terrestrial auroral case[Reference Speirs, Bingham, Cairns, Vorgul, Kellett, Phelps and Ronald24], this could result in R-mode like radiation propagating parallel to the magnetostatic field and an associated reduction in cyclotron-wave coupling efficiency for second harmonic absorption at the associated magnetic field resonance. Laboratory astrophysics is an exciting area pioneered by several groups[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22, Reference Drake25–Reference Gregori, Reville and Miniati29]. The scaling relationships that allow laboratory experiments to investigate astrophysical phenomena are well established and routinely used to devise laboratory parameter regimes that have astrophysical relevance[Reference Ryutov, Remington, Robey and Drake30]. Laboratory experiments conducted by Lebedev et al.
[Reference Lebedev, Suttle, Swadling, Bennett, Bland, Burdiak, Burgess, Chittenden, Ciardi, Clemens, de Grouchy, Hall, Hare, Kalmoni, Niasse, Patankar, Sheng, Smith, Suzuki-Vidal, Yuan, Frank, Blackman and Drake28] for the study of high speed plasma jets can in particular be comparatively considered with reference to astrophysical regimes via Ryutov’s scaling[Reference Ryutov, Remington, Robey and Drake30]. In the current context, the experiments that are described and reviewed in this article compare well with the astrophysical scenario under consideration. From this point, the paper is organised as follows. Section 2: we describe electron acceleration by lower hybrid waves at collisionless shocks. Section 3: we describe the cyclotron-maser emission model. Section 4: we summarise and review our findings and implications of the results.
$r_{m}$
is the radius of the jet at the emission region. Another consideration is the potential for refraction of the generated radiation due to the gradient in plasma density associated with the quasi-perpendicular shock. From our previous consideration for the terrestrial auroral case[Reference Speirs, Bingham, Cairns, Vorgul, Kellett, Phelps and Ronald24], this could result in R-mode like radiation propagating parallel to the magnetostatic field and an associated reduction in cyclotron-wave coupling efficiency for second harmonic absorption at the associated magnetic field resonance. Laboratory astrophysics is an exciting area pioneered by several groups[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22, Reference Drake25–Reference Gregori, Reville and Miniati29]. The scaling relationships that allow laboratory experiments to investigate astrophysical phenomena are well established and routinely used to devise laboratory parameter regimes that have astrophysical relevance[Reference Ryutov, Remington, Robey and Drake30]. Laboratory experiments conducted by Lebedev et al.
[Reference Lebedev, Suttle, Swadling, Bennett, Bland, Burdiak, Burgess, Chittenden, Ciardi, Clemens, de Grouchy, Hall, Hare, Kalmoni, Niasse, Patankar, Sheng, Smith, Suzuki-Vidal, Yuan, Frank, Blackman and Drake28] for the study of high speed plasma jets can in particular be comparatively considered with reference to astrophysical regimes via Ryutov’s scaling[Reference Ryutov, Remington, Robey and Drake30]. In the current context, the experiments that are described and reviewed in this article compare well with the astrophysical scenario under consideration. From this point, the paper is organised as follows. Section 2: we describe electron acceleration by lower hybrid waves at collisionless shocks. Section 3: we describe the cyclotron-maser emission model. Section 4: we summarise and review our findings and implications of the results.
2 Electron acceleration and cyclotron-maser emission
2.1 Electron acceleration by lower-hybrid waves
Lower-hybrid waves have been used in the laboratory for some time particularly with regard to generating high energy electron tails for current drive in tokamaks[Reference Cesario, Amicucci, Castaldo, Kempenaars, Jachmich, Mailloux, Tudisco, Galli and Krivska31]. They have also been associated with a number of space and astrophysics particle acceleration problems in particular collisionless shock acceleration in flares[Reference McClements, Bingham, Su, Dawson and Spicer11], bow shocks in magnetospheres[Reference Shapiro, Bingham, Dawson, Dobe, Kellett and Mendis32], supernova remnants[Reference Bingham, Kellett, Bryans, Summers, Torney, Shapiro, Spicer and O’Brien17], jets[Reference Bingham, Kellett, Cairns, Tonge and Mendonca4] and galaxy clusters. Although they have been inferred in satellite data from these systems for many years, laboratory experiments provide a controlled environment allowing reproducible results supporting space observations and validating data from simulation codes[Reference Cruz, Alves, Bamford, Bingham, Fonseca and Silva23]. The resonant interaction between lower-hybrid turbulence and electrons can result in field-aligned electron acceleration[Reference Laming12, Reference Vink and Laming13, Reference Omelchenko, Sagdeev, Shapiro and Shevchenko33–Reference Eilek35]. These waves are most probably excited by the modified two-stream instability[Reference Yamada and Owens10] resulting from the interaction between a collisionless shock and the ion species in the ambient plasma. In this interaction a pressure wave or shock wave forms resulting in the perturbation of ion trajectories and collective gyration due to acceleration with respect to the ambient magnetic field. These ions under the action of
![]() $\text{}\underline{E}\times \text{}\underline{B}$
evolve a monoenergetic ion ring distribution in the plasma. This distribution of ions drives the modified two-stream instability described by the following dispersion relation[Reference Shapiro, Bingham, Dawson, Dobe, Kellett and Mendis32, Reference Omelchenko, Sagdeev, Shapiro and Shevchenko33]
$\text{}\underline{E}\times \text{}\underline{B}$
evolve a monoenergetic ion ring distribution in the plasma. This distribution of ions drives the modified two-stream instability described by the following dispersion relation[Reference Shapiro, Bingham, Dawson, Dobe, Kellett and Mendis32, Reference Omelchenko, Sagdeev, Shapiro and Shevchenko33]
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x1D714}_{lh}^{2}}{\unicode[STIX]{x1D6FA}^{2}}+\frac{\unicode[STIX]{x1D714}_{ce}^{2}}{\unicode[STIX]{x1D6FA}^{2}}\frac{k_{\Vert }^{2}}{k^{2}+\unicode[STIX]{x1D714}_{pe}^{2}/c^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \qquad +\,8\unicode[STIX]{x1D70B}^{2}i\int \text{d}v_{\Vert }\int _{\unicode[STIX]{x1D6FA}/k_{\bot }}^{\infty }\text{d}v_{\bot }\frac{\unicode[STIX]{x2202}f_{p}/\unicode[STIX]{x2202}v_{\bot }}{\sqrt{k_{\bot }^{2}v_{\bot }^{2}-\unicode[STIX]{x1D6FA}^{2}}}\nonumber\\ \displaystyle & & \displaystyle \qquad =1+\frac{\unicode[STIX]{x1D714}_{pe}^{2}}{k^{2}c^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x1D714}_{lh}^{2}}{\unicode[STIX]{x1D6FA}^{2}}+\frac{\unicode[STIX]{x1D714}_{ce}^{2}}{\unicode[STIX]{x1D6FA}^{2}}\frac{k_{\Vert }^{2}}{k^{2}+\unicode[STIX]{x1D714}_{pe}^{2}/c^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \qquad +\,8\unicode[STIX]{x1D70B}^{2}i\int \text{d}v_{\Vert }\int _{\unicode[STIX]{x1D6FA}/k_{\bot }}^{\infty }\text{d}v_{\bot }\frac{\unicode[STIX]{x2202}f_{p}/\unicode[STIX]{x2202}v_{\bot }}{\sqrt{k_{\bot }^{2}v_{\bot }^{2}-\unicode[STIX]{x1D6FA}^{2}}}\nonumber\\ \displaystyle & & \displaystyle \qquad =1+\frac{\unicode[STIX]{x1D714}_{pe}^{2}}{k^{2}c^{2}},\end{eqnarray}$$
where
![]() $f_{p}(\unicode[STIX]{x1D710}_{\bot },\unicode[STIX]{x1D710}_{\Vert })$
is the distribution function of the reflected protons in terms of the perpendicular velocity
$f_{p}(\unicode[STIX]{x1D710}_{\bot },\unicode[STIX]{x1D710}_{\Vert })$
is the distribution function of the reflected protons in terms of the perpendicular velocity
![]() $v_{\bot }$
and axial velocity
$v_{\bot }$
and axial velocity
![]() $v_{\Vert }$
,
$v_{\Vert }$
,
![]() $\unicode[STIX]{x1D714}_{lh}$
is the lower-hybrid frequency,
$\unicode[STIX]{x1D714}_{lh}$
is the lower-hybrid frequency,
![]() $k_{\Vert }$
and
$k_{\Vert }$
and
![]() $k_{\bot }$
are the axial and perpendicular wavenumbers, respectively, and
$k_{\bot }$
are the axial and perpendicular wavenumbers, respectively, and
![]() $k$
is the wavenumber. We assumed that as a result of ion gyration in the ambient magnetic field, particles are completely mixed over phase of rotation and establish a gyrotropic distribution
$k$
is the wavenumber. We assumed that as a result of ion gyration in the ambient magnetic field, particles are completely mixed over phase of rotation and establish a gyrotropic distribution
![]() $f(v_{\bot },v_{\Vert })$
, contrary to the case of a nongyrotropic plane beam distribution. The instability excites lower-hybrid waves having the following dispersion law[Reference Omelchenko, Sagdeev, Shapiro and Shevchenko33]
$f(v_{\bot },v_{\Vert })$
, contrary to the case of a nongyrotropic plane beam distribution. The instability excites lower-hybrid waves having the following dispersion law[Reference Omelchenko, Sagdeev, Shapiro and Shevchenko33]
where
![]() $\unicode[STIX]{x1D6FD}=8\unicode[STIX]{x1D70B}n_{0}T_{e}/B_{0}^{2}$
is the ratio of the plasma kinetic pressure to the magnetic pressure,
$\unicode[STIX]{x1D6FD}=8\unicode[STIX]{x1D70B}n_{0}T_{e}/B_{0}^{2}$
is the ratio of the plasma kinetic pressure to the magnetic pressure,
![]() $\unicode[STIX]{x1D70C}=\sqrt{T_{e}/m_{e}}/\unicode[STIX]{x1D714}_{ce}$
is the electron gyroradius calculated with the electron temperature
$\unicode[STIX]{x1D70C}=\sqrt{T_{e}/m_{e}}/\unicode[STIX]{x1D714}_{ce}$
is the electron gyroradius calculated with the electron temperature
![]() $T_{e}$
,
$T_{e}$
,
![]() $m_{e}$
is the electron mass,
$m_{e}$
is the electron mass,
![]() $B_{0}$
is the magnetic flux density and
$B_{0}$
is the magnetic flux density and
![]() $n_{0}$
is the plasma density.
$n_{0}$
is the plasma density.
The integral over
![]() $v_{\bot }$
on the l.h.s. of Equation (1) can be easily calculated giving the following expression for the growth rate[Reference Shapiro, Bingham, Dawson, Dobe, Kellett and Mendis32], where
$v_{\bot }$
on the l.h.s. of Equation (1) can be easily calculated giving the following expression for the growth rate[Reference Shapiro, Bingham, Dawson, Dobe, Kellett and Mendis32], where
![]() $n_{rp}$
is the reflected proton density and
$n_{rp}$
is the reflected proton density and
![]() $m_{p}$
is the proton mass.
$m_{p}$
is the proton mass.
In order for the instability to be viable it needs to develop on a distance scale of
![]() $r\approx 10u/\unicode[STIX]{x1D6FE}_{gr}$
which must also be shorter than the physical dimensions of the interaction region, where
$r\approx 10u/\unicode[STIX]{x1D6FE}_{gr}$
which must also be shorter than the physical dimensions of the interaction region, where
![]() $u$
is the shock velocity (of order
$u$
is the shock velocity (of order
![]() $3\times 10^{7}~\text{m}\cdot \text{s}^{-1}$
in the case of the blazar jet). The corresponding distance scale
$3\times 10^{7}~\text{m}\cdot \text{s}^{-1}$
in the case of the blazar jet). The corresponding distance scale
![]() $r$
for generating the lower-hybrid turbulence would therefore be
$r$
for generating the lower-hybrid turbulence would therefore be
![]() ${\sim}$
30 km in the blazar jet environment.
${\sim}$
30 km in the blazar jet environment.
The wave spectrum is centred on the average energy
![]() $\unicode[STIX]{x1D700}_{e}$
, which can be obtained from energy balance between the ambient ions species and the accelerated electrons
$\unicode[STIX]{x1D700}_{e}$
, which can be obtained from energy balance between the ambient ions species and the accelerated electrons
![]() $\unicode[STIX]{x1D6FC}n_{rp}m_{p}u^{3}\approx n_{e}\unicode[STIX]{x1D700}_{e}(\unicode[STIX]{x1D700}_{e}/m_{e})^{1/2},$
where
$\unicode[STIX]{x1D6FC}n_{rp}m_{p}u^{3}\approx n_{e}\unicode[STIX]{x1D700}_{e}(\unicode[STIX]{x1D700}_{e}/m_{e})^{1/2},$
where
![]() $\unicode[STIX]{x1D6FC}$
is the transformation efficiency from reflected protons to electrons which we take as
$\unicode[STIX]{x1D6FC}$
is the transformation efficiency from reflected protons to electrons which we take as
![]() $0.1\%$
, their density
$0.1\%$
, their density
![]() $n_{e}$
can be estimated by balancing the growth rate of the instability initiated by ambient protons
$n_{e}$
can be estimated by balancing the growth rate of the instability initiated by ambient protons
![]() $\unicode[STIX]{x1D6FE}_{p}$
with Landau damping due to electrons
$\unicode[STIX]{x1D6FE}_{p}$
with Landau damping due to electrons
![]() $\unicode[STIX]{x1D6FE}_{e}$
moving parallel to the magnetic field,
$\unicode[STIX]{x1D6FE}_{e}$
moving parallel to the magnetic field,
Equation (4) can be rewritten as
and together with the above equation for the energy balance gives an estimate for the accelerated electron energy
![]() $\unicode[STIX]{x1D700}_{e}\approx \unicode[STIX]{x1D6FC}^{2/5}(m_{e}/m_{p})^{1/5}m_{p}u^{2}$
and their number density
$\unicode[STIX]{x1D700}_{e}\approx \unicode[STIX]{x1D6FC}^{2/5}(m_{e}/m_{p})^{1/5}m_{p}u^{2}$
and their number density
![]() $n_{e}\approx n_{rp}\unicode[STIX]{x1D6FC}^{2/5}(m_{e}/m_{i})^{1/5}$
[Reference Shapiro and Shevchenko14, Reference Bingham, Dawson, Shapiro, Mendis and Kellett15]. This corresponds to electron energies of 450 keV and a number density
$n_{e}\approx n_{rp}\unicode[STIX]{x1D6FC}^{2/5}(m_{e}/m_{i})^{1/5}$
[Reference Shapiro and Shevchenko14, Reference Bingham, Dawson, Shapiro, Mendis and Kellett15]. This corresponds to electron energies of 450 keV and a number density
![]() $n_{e}$
of
$n_{e}$
of
![]() $5\%$
of the reflected proton density
$5\%$
of the reflected proton density
![]() $n_{rp}$
.
$n_{rp}$
.
Recent PIC simulations conducted by using OSIRIS[Reference Cruz, Alves, Bamford, Bingham, Fonseca and Silva23] predicted electron acceleration via lower-hybrid turbulence of
![]() $\unicode[STIX]{x1D700}_{e}^{\text{PIC}}\sim 75~\text{keV}$
while an associated scaled laboratory experiment[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22] (with differing electron-ion mass ratio and ion velocity
$\unicode[STIX]{x1D700}_{e}^{\text{PIC}}\sim 75~\text{keV}$
while an associated scaled laboratory experiment[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22] (with differing electron-ion mass ratio and ion velocity
![]() $u$
) demonstrated electron energization to
$u$
) demonstrated electron energization to
![]() $\unicode[STIX]{x1D700}_{e}^{\text{LAB}}\sim 45~\text{eV}$
. This new laboratory experiment[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22] confirmed that the analytical estimates for the average energy
$\unicode[STIX]{x1D700}_{e}^{\text{LAB}}\sim 45~\text{eV}$
. This new laboratory experiment[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22] confirmed that the analytical estimates for the average energy
![]() $\unicode[STIX]{x1D716}_{e}$
and number density
$\unicode[STIX]{x1D716}_{e}$
and number density
![]() $n_{e}$
of accelerated electrons (described by the equations above) are in good agreement with the experimental results, as were the numerical simulations[Reference Cruz, Alves, Bamford, Bingham, Fonseca and Silva23]. This strengthens the theoretical model describing lower-hybrid electron acceleration at collisionless shocks predicted by a number of authors. In Ref. [Reference Begelman, Ergun and Rees3], it is argued that electrons accelerated at collisionless shocks have the possibility of being magnetically compressed giving rise to horseshoe-type electron velocity distribution functions which are unstable to the generation of maser radiation[Reference Begelman, Ergun and Rees3–Reference Treumann5, Reference Bingham and Cairns36]. Some of the present authors have conducted extensive laboratory experiments to study maser radiation from electron horseshoe/ring distributions[Reference Ronald, Speirs, McConville, Phelps, Robertson, Whyte, He, Gillespie, Cross and Bingham37–Reference McConville, Speirs, Ronald, Phelps, Cross, Bingham, Robertson, Whyte, He, Gillespie, Vorgul, Cairns and Kellett39]. They adopted an electron energy (
$n_{e}$
of accelerated electrons (described by the equations above) are in good agreement with the experimental results, as were the numerical simulations[Reference Cruz, Alves, Bamford, Bingham, Fonseca and Silva23]. This strengthens the theoretical model describing lower-hybrid electron acceleration at collisionless shocks predicted by a number of authors. In Ref. [Reference Begelman, Ergun and Rees3], it is argued that electrons accelerated at collisionless shocks have the possibility of being magnetically compressed giving rise to horseshoe-type electron velocity distribution functions which are unstable to the generation of maser radiation[Reference Begelman, Ergun and Rees3–Reference Treumann5, Reference Bingham and Cairns36]. Some of the present authors have conducted extensive laboratory experiments to study maser radiation from electron horseshoe/ring distributions[Reference Ronald, Speirs, McConville, Phelps, Robertson, Whyte, He, Gillespie, Cross and Bingham37–Reference McConville, Speirs, Ronald, Phelps, Cross, Bingham, Robertson, Whyte, He, Gillespie, Vorgul, Cairns and Kellett39]. They adopted an electron energy (
![]() ${\sim}$
50–100 keV) and magnetic flux density (
${\sim}$
50–100 keV) and magnetic flux density (
![]() ${\sim}$
0.5 T) similar to those associated with the blazar jet parameters[Reference Begelman, Ergun and Rees3]. The experimental details of maser radiation from accelerated electrons are reported in Section 3.
${\sim}$
0.5 T) similar to those associated with the blazar jet parameters[Reference Begelman, Ergun and Rees3]. The experimental details of maser radiation from accelerated electrons are reported in Section 3.
2.2 Electron cyclotron-maser instability
In this section we consider the stability of a horseshoe shaped electron velocity distribution with respect to a cyclotron-maser instability resulting in R-X mode waves propagating perpendicularly to a magnetostatic field[Reference Bingham and Cairns36, Reference Melrose40]. To obtain the horseshoe distribution function, we consider a drifting Maxwellian having a drift velocity well above the thermal speed. This is typical for electrons accelerated by lower-hybrid turbulence. The particle population then moves into an increasing magnetic field where the distribution function is readily calculated by conservation of total energy and magnetic moment. We use the resulting distribution function in the dispersion relation for the R-X mode, obtainable from the susceptibility tensor given by Ref. [Reference Stix41], assuming that the frequency is close to the electron-cyclotron frequency and that the Larmor radius for typical electron velocities is much less than the wavelength of the wave. We need only consider the susceptibility to lowest order in
![]() $k_{\bot }v_{\bot }/\unicode[STIX]{x1D714}_{ce}$
as a result of this latter condition. Neglecting all but the zero-order terms, we get the cold plasma result[Reference Stix41]. To a first approximation, it is only necessary to account for the velocity distribution of the electrons in the resonant integral involving
$k_{\bot }v_{\bot }/\unicode[STIX]{x1D714}_{ce}$
as a result of this latter condition. Neglecting all but the zero-order terms, we get the cold plasma result[Reference Stix41]. To a first approximation, it is only necessary to account for the velocity distribution of the electrons in the resonant integral involving
![]() $1/(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{ce})$
, where
$1/(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{ce})$
, where
![]() $\unicode[STIX]{x1D714}_{ce}$
is the relativistic electron-cyclotron frequency
$\unicode[STIX]{x1D714}_{ce}$
is the relativistic electron-cyclotron frequency
![]() $eB/\unicode[STIX]{x1D6FE}m_{e}$
, with
$eB/\unicode[STIX]{x1D6FE}m_{e}$
, with
![]() $e$
the electron charge,
$e$
the electron charge,
![]() $B$
the magnetic field,
$B$
the magnetic field,
![]() $\unicode[STIX]{x1D6FE}$
the Lorentz factor, and
$\unicode[STIX]{x1D6FE}$
the Lorentz factor, and
![]() $m_{e}$
the electron rest mass. We must account for the relativistic shift of the cyclotron frequency in the resonant term, as this picks out a particular group of resonant electrons and results in either damping or growth of the wave. In terms of momentum
$m_{e}$
the electron rest mass. We must account for the relativistic shift of the cyclotron frequency in the resonant term, as this picks out a particular group of resonant electrons and results in either damping or growth of the wave. In terms of momentum
![]() $p$
we have
$p$
we have
where
![]() $\unicode[STIX]{x1D714}_{e0}$
is the non-relativistic electron-cyclotron frequency. We can simply take the cold plasma result for the real part of the resonant integral. Although this is proportional to
$\unicode[STIX]{x1D714}_{e0}$
is the non-relativistic electron-cyclotron frequency. We can simply take the cold plasma result for the real part of the resonant integral. Although this is proportional to
![]() $1/(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{e0})$
and appears to be near-singular at the resonance, the
$1/(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{e0})$
and appears to be near-singular at the resonance, the
![]() $1/(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{e0})$
factors in the real part of the dispersion relation cancel out, resulting in smooth behaviour in the vicinity of the cyclotron frequency. Small corrections to the cyclotron frequency are not necessary in the real part of the dispersion relation. The refractive index
$1/(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{e0})$
factors in the real part of the dispersion relation cancel out, resulting in smooth behaviour in the vicinity of the cyclotron frequency. Small corrections to the cyclotron frequency are not necessary in the real part of the dispersion relation. The refractive index
![]() $N$
for the R-X mode, which propagates perpendicularly to the magnetostatic field, is well known and given by Ref. [Reference Stix41],
$N$
for the R-X mode, which propagates perpendicularly to the magnetostatic field, is well known and given by Ref. [Reference Stix41],
with the dielectric tensor elements given by
and
 $$\begin{eqnarray}\displaystyle A & = & \displaystyle \frac{1}{4}\frac{\unicode[STIX]{x1D714}_{pe}^{2}}{\unicode[STIX]{x1D714}}\int _{0}^{\infty }2\unicode[STIX]{x1D70B}p_{\bot }\,\text{d}p_{\bot }\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{-\infty }^{\infty }\text{d}p_{\Vert }\frac{1}{\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{ce}}p_{\bot }\frac{\unicode[STIX]{x2202}f_{e}}{\unicode[STIX]{x2202}p_{\bot }}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A & = & \displaystyle \frac{1}{4}\frac{\unicode[STIX]{x1D714}_{pe}^{2}}{\unicode[STIX]{x1D714}}\int _{0}^{\infty }2\unicode[STIX]{x1D70B}p_{\bot }\,\text{d}p_{\bot }\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{-\infty }^{\infty }\text{d}p_{\Vert }\frac{1}{\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{ce}}p_{\bot }\frac{\unicode[STIX]{x2202}f_{e}}{\unicode[STIX]{x2202}p_{\bot }}.\end{eqnarray}$$
In order to obtain this we have only included the 1st terms in the sum over harmonics, and used the small argument expansion
![]() $J_{1}(x)\approx x/2$
, where
$J_{1}(x)\approx x/2$
, where
![]() $x=k_{\bot }v_{\bot }/\unicode[STIX]{x1D714}_{ce}$
. If we switch to spherical polar coordinates
$x=k_{\bot }v_{\bot }/\unicode[STIX]{x1D714}_{ce}$
. If we switch to spherical polar coordinates
![]() $(p,\unicode[STIX]{x1D707},\unicode[STIX]{x1D719})$
, and substitute the usual angle
$(p,\unicode[STIX]{x1D707},\unicode[STIX]{x1D719})$
, and substitute the usual angle
![]() $\unicode[STIX]{x1D703}$
with
$\unicode[STIX]{x1D703}$
with
![]() $\unicode[STIX]{x1D707}=\cos \unicode[STIX]{x1D703}=p_{\Vert }/p$
we then get
$\unicode[STIX]{x1D707}=\cos \unicode[STIX]{x1D703}=p_{\Vert }/p$
we then get
 $$\begin{eqnarray}\displaystyle A & = & \displaystyle -\frac{1}{2}\frac{\unicode[STIX]{x1D714}_{pe}^{2}}{\unicode[STIX]{x1D714}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{e0})}-\frac{i}{2}\frac{\unicode[STIX]{x1D714}_{pe}^{2}}{\unicode[STIX]{x1D714}_{e0}}\int _{1}^{-1}(1-\unicode[STIX]{x1D707}^{2})p_{0}^{2}\unicode[STIX]{x1D6FE}_{0}^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\left(\frac{\unicode[STIX]{x2202}f_{e}}{\unicode[STIX]{x2202}p}-\frac{\unicode[STIX]{x1D707}}{p_{0}}\frac{\unicode[STIX]{x2202}f_{e}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right)_{|p=p_{0}|}\,\text{d}\unicode[STIX]{x1D707},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A & = & \displaystyle -\frac{1}{2}\frac{\unicode[STIX]{x1D714}_{pe}^{2}}{\unicode[STIX]{x1D714}(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{e0})}-\frac{i}{2}\frac{\unicode[STIX]{x1D714}_{pe}^{2}}{\unicode[STIX]{x1D714}_{e0}}\int _{1}^{-1}(1-\unicode[STIX]{x1D707}^{2})p_{0}^{2}\unicode[STIX]{x1D6FE}_{0}^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\left(\frac{\unicode[STIX]{x2202}f_{e}}{\unicode[STIX]{x2202}p}-\frac{\unicode[STIX]{x1D707}}{p_{0}}\frac{\unicode[STIX]{x2202}f_{e}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right)_{|p=p_{0}|}\,\text{d}\unicode[STIX]{x1D707},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FE}=(1+p^{2})^{1/2}$
and
$\unicode[STIX]{x1D6FE}=(1+p^{2})^{1/2}$
and
![]() $p_{0}$
is the resonant momentum,
$p_{0}$
is the resonant momentum,
![]() $p_{0}=m_{e}c[2(\unicode[STIX]{x1D714}_{e0}-\unicode[STIX]{x1D714})/\unicode[STIX]{x1D714}_{ce}]^{1/2}$
. A complete analysis of the dispersion relation for waves propagating perpendicularly to the magnetostatic field can be found in Ref. [Reference Stix41].
$p_{0}=m_{e}c[2(\unicode[STIX]{x1D714}_{e0}-\unicode[STIX]{x1D714})/\unicode[STIX]{x1D714}_{ce}]^{1/2}$
. A complete analysis of the dispersion relation for waves propagating perpendicularly to the magnetostatic field can be found in Ref. [Reference Stix41].
From Equations (8), (9) and (10) we can examine the stability of Equation (7) with respect to induced emission of right hand polarized radiation.

Figure 1. Perpendicular and parallel components of electron momentum (normalized to the mean electron momentum
![]() $p_{e0}$
) for an evolved horseshoe distribution function, with the contours representing constant phase-space density.
$p_{e0}$
) for an evolved horseshoe distribution function, with the contours representing constant phase-space density.
We consider the initial beam to be a drifting Maxwellian moving into a strong magnetic field region. Figure 1 illustrates the characteristic horseshoe or crescent distribution generated when the beam moves into a stronger field region. Using the distribution shown in Figure 1, we obtain the spatial growth rate shown in Figure 2 for two different beam energies. The imaginary part of the refractive index is plotted as a function of frequency for mean beam energies of 100 keV and 500 keV, both with a 1% energy spread and a magnetic field ratio of 20. Unstable wave growth occurs for (and in proportion to) negative values for the imaginary part of the refractive index. With reference to Figure 2, the maximum growth rate for the 500 keV beam is therefore more than 5 times greater than for the 100 keV beam, with a growth spectral bandwidth that is around 10 times larger. The analysis presented above considers strictly perpendicular propagation. We also calculated the growth rates for modes that contain a parallel wavenumber component, finding that modes that propagate more than about
![]() $50^{\circ }$
to the perpendicular direction do not grow. We find that the fastest growing component is for propagation purely perpendicular to the magnetostatic field. The region of instability in frequency space is extremely narrow with a bandwidth
$50^{\circ }$
to the perpendicular direction do not grow. We find that the fastest growing component is for propagation purely perpendicular to the magnetostatic field. The region of instability in frequency space is extremely narrow with a bandwidth
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}$
on the order of 0.5%.
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}$
on the order of 0.5%.
It should be noted that the wave emission due to a horseshoe or ring distribution is primarily in the plane perpendicular to the magnetic field, spectrally close to the electron-cyclotron frequency. For higher electron energies the frequency decreases due to the relativistic mass increase, clearly evident when comparing the maximum growth rates shown in Figure 2. A parallel component of wavenumber incorporates a Doppler shift into the resonance condition, resulting in the resonant particles no longer lying on a sphere in momentum space, centred on the origin. The implications are that for any significant Doppler shift, resonant particles will no longer lie in the portion of the electron velocity distribution for which there is a positive slope. The growth rate therefore falls off as we move away from perpendicular propagation, with the peak wave emission expected in the plane perpendicular to the magnetostatic field. As expected the instability is sensitive to the ratio of the electron-cyclotron frequency to the plasma frequency
![]() $\unicode[STIX]{x1D714}_{ce}/\unicode[STIX]{x1D714}_{pe}$
. For
$\unicode[STIX]{x1D714}_{ce}/\unicode[STIX]{x1D714}_{pe}$
. For
![]() $\unicode[STIX]{x1D714}_{ce}\gg \unicode[STIX]{x1D714}_{pe}$
we expect strong growth occurring in a low background plasma density, where beam instabilities are not strong enough to disrupt the electron velocity and spatial distribution. Typically, beam instabilities have growth rates that are proportional to
$\unicode[STIX]{x1D714}_{ce}\gg \unicode[STIX]{x1D714}_{pe}$
we expect strong growth occurring in a low background plasma density, where beam instabilities are not strong enough to disrupt the electron velocity and spatial distribution. Typically, beam instabilities have growth rates that are proportional to
![]() $n_{e}^{1/3}$
[Reference Krall and Trivelpiece42], whereas the instability described here is not strongly dependent on density.
$n_{e}^{1/3}$
[Reference Krall and Trivelpiece42], whereas the instability described here is not strongly dependent on density.

Figure 2. Imaginary part of the refractive index as a function of frequency for a mean beam energy of 100 keV and a thermal spread of 1 keV, and a mean beam energy of 500 keV and a thermal spread of 5 keV. The magnetic field ratio is taken to be 20.
3 Simulations and laboratory experiment of maser emission
The idea that collisionless shock waves can accelerate electrons to high energy along the magnetic field direction has been demonstrated in a recent laboratory experiment using high energy lasers[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22]. Modern high-power lasers are unique tools that are able to deliver pulses that have enormous energy densities to target. They allow measurements of plasma conditions that are of astrophysical interest, and allow testing the complex models of these processes with unprecedented precision. Laser-plasma results have been applied to the study of such diverse environments as active galactic nuclei and the Earth’s bow shock. More recent applications include the hydrodynamics of supernovae, supernova remnants and the collision of galactic clouds[Reference Scopatz, Fatenejad, Flocke, Gregori, Koenig, Lamb, Lee, Meinecke, Ravasio, Tzeferacos, Weide and Yurchak43, Reference Meinecke, Doyle, Miniati, Bell, Bingham, Crowston, Drake, Fatenejad, Koenig, Kuramitsu, Kuranz, Lamb, Lee, MacDonald, Murphy, Park, Pelka, Ravasio, Sakawa, Schekochihin, Scopatz, Tzeferacos, Wan, Woolsey, Yurchak, Reville and Gregori44]. Such experiments are made possible by ensuring that certain key dimensionless parameters in the laser-generated plasmas have values similar to those of the space and astrophysical plasmas of interest. A recent paper in Nature Physics
[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22] reports on results from an experiment to investigate energetic particle production and X-ray emission from collisionless shock waves. In the experiment a 1 kJ, 1.5 ns laser beam of wavelength 527 nm impacted a 50
![]() $\unicode[STIX]{x03BC}\text{m}$
thick PVDF (
$\unicode[STIX]{x03BC}\text{m}$
thick PVDF (
![]() $\text{C}_{2}\text{H}_{2}\text{F}_{2}$
) foil target producing a high speed expanding plasma on the back surface with a velocity of 70 km/s. A 12-mm-diameter sphere was placed 15 mm from the foil, fabricated from either magnetized Nd with an approximately 7 kG surface field or unmagnetized glass. The fluorine ions within the expanding plasma have a kinetic energy of about 500 keV. When this plasma flow impacted the magnetized neodymium sphere, a strong collisionless bow shock formed
$\text{C}_{2}\text{H}_{2}\text{F}_{2}$
) foil target producing a high speed expanding plasma on the back surface with a velocity of 70 km/s. A 12-mm-diameter sphere was placed 15 mm from the foil, fabricated from either magnetized Nd with an approximately 7 kG surface field or unmagnetized glass. The fluorine ions within the expanding plasma have a kinetic energy of about 500 keV. When this plasma flow impacted the magnetized neodymium sphere, a strong collisionless bow shock formed
![]() ${\sim}2.5~\text{mm}$
upstream of the object. Interferometric data showed that the bulk electron density increased from
${\sim}2.5~\text{mm}$
upstream of the object. Interferometric data showed that the bulk electron density increased from
![]() ${\sim}10^{17}~\text{cm}^{-3}$
in the upstream region to
${\sim}10^{17}~\text{cm}^{-3}$
in the upstream region to
![]() ${\sim}10^{18}~\text{cm}^{-3}$
in the downstream region with a bulk plasma temperature of about 3 eV. An
${\sim}10^{18}~\text{cm}^{-3}$
in the downstream region with a bulk plasma temperature of about 3 eV. An
![]() $x$
–
$x$
–
![]() $y$
spectrometer spatially resolved along the flow axis recorded soft X-rays in the range 630–770 eV including the fluorine line. This excess of X-rays is an indication that electrons with energies significantly greater than 3 eV must be present. No such results were observed with the un-magnetized sphere. To fully understand the interaction between the flowing plasma and a small magnetized object and assist in the experimental analysis, simulations were carried out using two numerical codes[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22, Reference Cruz, Alves, Bamford, Bingham, Fonseca and Silva23]. A two-dimensional radiation-hydrodynamic code FLASH[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22] was used together with a full PIC code OSIRIS[Reference Cruz, Alves, Bamford, Bingham, Fonseca and Silva23]. The results from FLASH were in qualitative agreement with experiment, predicting the electric field influence on the plasma near the shock from the simulated magnetic field and ion density[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22]. Experimental measurements inferred a super-critical shock with Mach number of
$y$
spectrometer spatially resolved along the flow axis recorded soft X-rays in the range 630–770 eV including the fluorine line. This excess of X-rays is an indication that electrons with energies significantly greater than 3 eV must be present. No such results were observed with the un-magnetized sphere. To fully understand the interaction between the flowing plasma and a small magnetized object and assist in the experimental analysis, simulations were carried out using two numerical codes[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22, Reference Cruz, Alves, Bamford, Bingham, Fonseca and Silva23]. A two-dimensional radiation-hydrodynamic code FLASH[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22] was used together with a full PIC code OSIRIS[Reference Cruz, Alves, Bamford, Bingham, Fonseca and Silva23]. The results from FLASH were in qualitative agreement with experiment, predicting the electric field influence on the plasma near the shock from the simulated magnetic field and ion density[Reference Rigby, Cruz, Albertazzi, Bamford, Bell, Cross, Fraschetti, Graham, Hara, Kozlowski, Kuramitsu, Lamb, Lebedev, Marques, Miniati, Morita, Oliver, Reville, Sakawa, Sarkar, Spindloe, Trines, Tzeferacos, Silva, Bingham, Koenig and Gregori22]. Experimental measurements inferred a super-critical shock with Mach number of
![]() ${\sim}5.7$
, necessitating a significant reflected ion component. OSIRIS was able to determine the kinetics of the interaction demonstrating the formation of a shock, generation of an electric field resulting in reflection of ions, generation of lower hybrid waves and electron energization along the direction of the magnetic field[Reference Cruz, Alves, Bamford, Bingham, Fonseca and Silva23]. These accelerated electrons, when moving into a stronger magnetic field, can evolve an unstable, pitch-spread velocity distribution having a horseshoe profile and capable of driving a cyclotron-maser instability that generates intense radio-frequency (RF) emission.
${\sim}5.7$
, necessitating a significant reflected ion component. OSIRIS was able to determine the kinetics of the interaction demonstrating the formation of a shock, generation of an electric field resulting in reflection of ions, generation of lower hybrid waves and electron energization along the direction of the magnetic field[Reference Cruz, Alves, Bamford, Bingham, Fonseca and Silva23]. These accelerated electrons, when moving into a stronger magnetic field, can evolve an unstable, pitch-spread velocity distribution having a horseshoe profile and capable of driving a cyclotron-maser instability that generates intense radio-frequency (RF) emission.

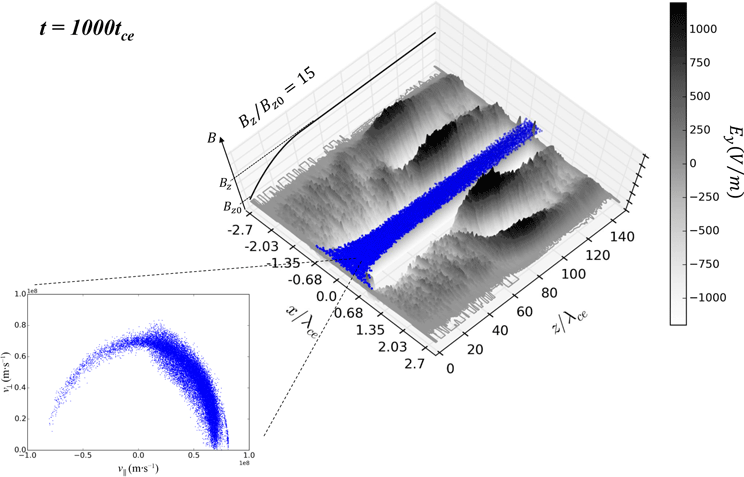
Figure 3. Composite overview of 3D VSim PIC simulation results in an
![]() $x$
–
$x$
–
![]() $z$
plane (
$z$
plane (
![]() $y=0$
) showing magnetic compression of an electron beam and subsequent cyclotron-maser emission in the X-mode at
$y=0$
) showing magnetic compression of an electron beam and subsequent cyclotron-maser emission in the X-mode at
![]() $t=1000t_{ce}$
. The electron PIC particle trajectory is also overlaid (blue scatter plot) along with the corresponding velocity distribution over the simulation volume at
$t=1000t_{ce}$
. The electron PIC particle trajectory is also overlaid (blue scatter plot) along with the corresponding velocity distribution over the simulation volume at
![]() $t=1000t_{ce}$
.
$t=1000t_{ce}$
.
Laboratory experiments[Reference Ronald, Speirs, McConville, Phelps, Robertson, Whyte, He, Gillespie, Cross and Bingham37, Reference McConville, Speirs, Ronald, Phelps, Cross, Bingham, Robertson, Whyte, He, Gillespie, Vorgul, Cairns and Kellett39] and PIC simulations[Reference Speirs, Bingham, Cairns, Vorgul, Kellett, Phelps and Ronald24, Reference Speirs, McConville, Gillespie, Ronald, Phelps, Cross, Bingham, Robertson, Whyte and Vorgul38, Reference Speirs, Ronald, McConville, Gillespie, Phelps, Cross, Bingham, Robertson, Whyte, He, Vorgul, Cairns and Kellett45] have demonstrated the high efficiency of the cyclotron-maser instability driven by electron horseshoe and ring-like velocity distributions. New numerical simulations have been carried out using the PIC code VSim[Reference Nieter and Cary46], with the simulation geometry comprising a 3D Cartesian gridded region with axial length of
![]() $144\unicode[STIX]{x1D706}_{ce}$
(where
$144\unicode[STIX]{x1D706}_{ce}$
(where
![]() $\unicode[STIX]{x1D706}_{ce}$
is the vacuum wavelength of radiation at the peak electron-cyclotron frequency within the simulation), symmetric transverse dimensions of
$\unicode[STIX]{x1D706}_{ce}$
is the vacuum wavelength of radiation at the peak electron-cyclotron frequency within the simulation), symmetric transverse dimensions of
![]() $2.7\unicode[STIX]{x1D706}_{ce}$
and perfectly matched-layer boundaries in
$2.7\unicode[STIX]{x1D706}_{ce}$
and perfectly matched-layer boundaries in
![]() $x,y$
and
$x,y$
and
![]() $z$
to prevent reflection and the formation of boundary resonant eigenmodes. Particle absorbent boundaries are also used in
$z$
to prevent reflection and the formation of boundary resonant eigenmodes. Particle absorbent boundaries are also used in
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
to terminate electron trajectories. An electron beam with energy 20 keV was injected parallel to an axial magnetic field that increased by a factor of 15 over
$z$
to terminate electron trajectories. An electron beam with energy 20 keV was injected parallel to an axial magnetic field that increased by a factor of 15 over
![]() $45\unicode[STIX]{x1D706}_{ce}$
, with the peak magnetic flux density of 0.1 T plateauing over the remaining
$45\unicode[STIX]{x1D706}_{ce}$
, with the peak magnetic flux density of 0.1 T plateauing over the remaining
![]() $99\unicode[STIX]{x1D706}_{ce}$
, an electron number density
$99\unicode[STIX]{x1D706}_{ce}$
, an electron number density
![]() $n_{e}$
of
$n_{e}$
of
![]() ${\sim}2.5\times 10^{14}~\text{m}^{-3}$
at the peak magnetic flux density and corresponding electron-cyclotron frequency to plasma frequency ratio of 20.
${\sim}2.5\times 10^{14}~\text{m}^{-3}$
at the peak magnetic flux density and corresponding electron-cyclotron frequency to plasma frequency ratio of 20.
Figure 3 shows the transverse-electric field profile
![]() $E_{y}$
as a surface plot in an
$E_{y}$
as a surface plot in an
![]() $x$
–
$x$
–
![]() $z$
plane for 2% injected electron energy spread. The electron PIC particle trajectory is superimposed along with a projection of the axial magnetostatic field profile
$z$
plane for 2% injected electron energy spread. The electron PIC particle trajectory is superimposed along with a projection of the axial magnetostatic field profile
![]() $B_{z}$
in the left-vertical plane. The injected electrons are subject to significant magnetic compression, forming a horseshoe shaped velocity distribution upon entry to the peak-plateau region at
$B_{z}$
in the left-vertical plane. The injected electrons are subject to significant magnetic compression, forming a horseshoe shaped velocity distribution upon entry to the peak-plateau region at
![]() ${\sim}45\unicode[STIX]{x1D706}_{ce}$
in
${\sim}45\unicode[STIX]{x1D706}_{ce}$
in
![]() $z$
. From around
$z$
. From around
![]() $75\unicode[STIX]{x1D706}_{ce}$
to
$75\unicode[STIX]{x1D706}_{ce}$
to
![]() $140\unicode[STIX]{x1D706}_{ce}$
in
$140\unicode[STIX]{x1D706}_{ce}$
in
![]() $z$
, there is clear evidence of cyclotron-maser emission in the X-mode, with wavefronts propagating near-perpendicularly to the axial magnetic field.
$z$
, there is clear evidence of cyclotron-maser emission in the X-mode, with wavefronts propagating near-perpendicularly to the axial magnetic field.

Figure 4. 3D VSim PIC simulation results showing (a) the spectrum of EM emission at
![]() $z=86\unicode[STIX]{x1D706}_{ce}$
and (b) the transverse Poynting flux in a
$z=86\unicode[STIX]{x1D706}_{ce}$
and (b) the transverse Poynting flux in a
![]() $y$
–
$y$
–
![]() $z$
plane displaced from the electron beam.
$z$
plane displaced from the electron beam.
The corresponding wave spectrum is plotted in Figure 4(a), showing the fast Fourier transform (FFT) of
![]() $E_{y}$
at
$E_{y}$
at
![]() $z=86\unicode[STIX]{x1D706}_{ce}$
over
$z=86\unicode[STIX]{x1D706}_{ce}$
over
![]() $t=0\rightarrow 1000t_{ce}$
. A single spectral component is present at
$t=0\rightarrow 1000t_{ce}$
. A single spectral component is present at
![]() $\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{ce}=1$
, corresponding to narrowband emission at the relativistic electron-cyclotron frequency. The corresponding transverse Poynting flux over a
$\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{ce}=1$
, corresponding to narrowband emission at the relativistic electron-cyclotron frequency. The corresponding transverse Poynting flux over a
![]() $y$
–
$y$
–
![]() $z$
plane in Figure 4(b) demonstrates a temporal modulation of the wave emission, with a
$z$
plane in Figure 4(b) demonstrates a temporal modulation of the wave emission, with a
![]() $350t_{ce}$
lead time for significant growth of the RF Poynting flux. A peak saturated output power of
$350t_{ce}$
lead time for significant growth of the RF Poynting flux. A peak saturated output power of
![]() $P/P_{beam}=1.13\times 10^{-2}$
is observed. When integrated over the transverse dimensions of the system (factoring in the 4 enclosing Poynting flux planes) this corresponds to an RF conversion efficiency of 4.50% which is in agreement with estimates from theory and consistent with estimates for the auroral kilometric radiation (AKR) generation efficiency[Reference Gurnett7].
$P/P_{beam}=1.13\times 10^{-2}$
is observed. When integrated over the transverse dimensions of the system (factoring in the 4 enclosing Poynting flux planes) this corresponds to an RF conversion efficiency of 4.50% which is in agreement with estimates from theory and consistent with estimates for the auroral kilometric radiation (AKR) generation efficiency[Reference Gurnett7].

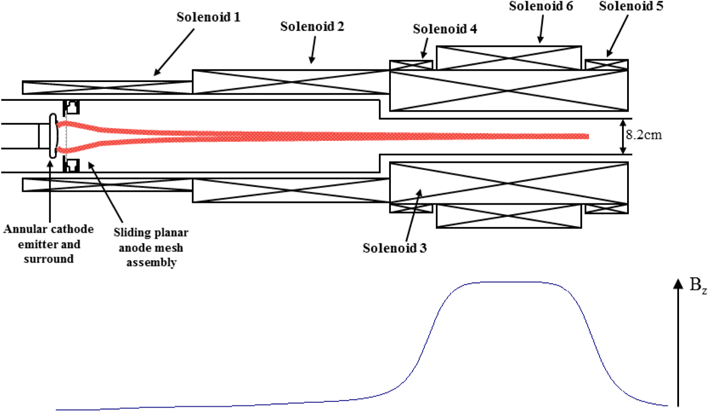
Figure 5. Diagrammatic overview of the experimental setup showing the magnetic coil configuration, electron gun and the convergent axial magnetic field profile with peak-plateau region for cyclotron resonant energy transfer.
A scaled laboratory experiment conducted at the University of Strathclyde, Glasgow, UK demonstrated the principles of electron beam magnetic compression/horseshoe formation and cyclotron-maser emission at microwave frequencies[Reference Speirs, Bingham, Cairns, Vorgul, Kellett, Phelps and Ronald24, Reference Ronald, Speirs, McConville, Phelps, Robertson, Whyte, He, Gillespie, Cross and Bingham37–Reference McConville, Speirs, Ronald, Phelps, Cross, Bingham, Robertson, Whyte, He, Gillespie, Vorgul, Cairns and Kellett39]. A schematic overview of the experiment is presented in Figure 5, showing the annular electron beam injected into a convergent magnetic field (with magnetic mirror ratios ranging from 15 to 30). The beam traversed into a circular-cylindrical waveguide post-compression, where excitation of X-mode like transverse-electric (TE) modes near cutoff (
![]() $k_{\Vert }\approx 0$
) occurred via the cyclotron-maser instability. Figure 6 shows the spectral output for a peak magnetic flux density of 0.18 T. A primary spectral peak is present at the electron-cyclotron frequency (4.42 GHz) and a small second harmonic peak at around 8.8 GHz. The corresponding output power for this experiment was 30 kW, equating to a beam-wave conversion efficiency of 1%[Reference McConville, Speirs, Ronald, Phelps, Cross, Bingham, Robertson, Whyte, He, Gillespie, Vorgul, Cairns and Kellett39]. Both the spectral output and beam-wave conversion efficiencies are consistent with the predictions of theory[Reference Bingham and Cairns36] and PIC simulations[Reference Speirs, Bingham, Cairns, Vorgul, Kellett, Phelps and Ronald24, Reference Speirs, McConville, Gillespie, Ronald, Phelps, Cross, Bingham, Robertson, Whyte and Vorgul38].
$k_{\Vert }\approx 0$
) occurred via the cyclotron-maser instability. Figure 6 shows the spectral output for a peak magnetic flux density of 0.18 T. A primary spectral peak is present at the electron-cyclotron frequency (4.42 GHz) and a small second harmonic peak at around 8.8 GHz. The corresponding output power for this experiment was 30 kW, equating to a beam-wave conversion efficiency of 1%[Reference McConville, Speirs, Ronald, Phelps, Cross, Bingham, Robertson, Whyte, He, Gillespie, Vorgul, Cairns and Kellett39]. Both the spectral output and beam-wave conversion efficiencies are consistent with the predictions of theory[Reference Bingham and Cairns36] and PIC simulations[Reference Speirs, Bingham, Cairns, Vorgul, Kellett, Phelps and Ronald24, Reference Speirs, McConville, Gillespie, Ronald, Phelps, Cross, Bingham, Robertson, Whyte and Vorgul38].

Figure 6. Experimental measurements for the TE01 resonance, illustrating the spectrum of the output signal, displaying a strong resonance close to the electron-cyclotron frequency, 4.42 GHz.
4 Summary and conclusions
In this article, we have described an acceleration scheme by which electrons may be energized at collisionless shocks. Propagation of these electrons into stronger magnetic field regions results in the formation of a horseshoe or thermal-ring-like distribution in velocity space. We outline a model by which such distributions can become unstable to a cyclotron-maser instability resulting in intense, narrowband radio emission in the X-mode with an efficiency of a few percent. In particular, the combination of lower-hybrid acceleration within collisionless shocks, diffusion of energetic electrons into increasing magnetic fields and the subsequent cyclotron-maser destabilization of the resultant electron velocity distributions provides an excellent framework for explaining radio emission from astrophysical jets, consistent with the suggestions of Begelman, Ergun and Rees[Reference Begelman, Ergun and Rees3]. We report on recent laboratory experiments[Reference Ronald, Speirs, McConville, Phelps, Robertson, Whyte, He, Gillespie, Cross and Bingham37–Reference McConville, Speirs, Ronald, Phelps, Cross, Bingham, Robertson, Whyte, He, Gillespie, Vorgul, Cairns and Kellett39] where energetic electrons with horseshoe-type distribution functions are unstable to the generation of maser radiation. Through theory, numerical simulations[Reference Cruz, Alves, Bamford, Bingham, Fonseca and Silva23, Reference Speirs, Bingham, Cairns, Vorgul, Kellett, Phelps and Ronald24, Reference Speirs, Ronald, McConville, Gillespie, Phelps, Cross, Bingham, Robertson, Whyte, He, Vorgul, Cairns and Kellett45, Reference Bingham, Speirs, Kellett, Vorgul, McConville, Cairns, Cross, Phelps and Ronald47] and laboratory experiments, the sub-elements and principal physics of this model have been explored. The results are relevant to a variety of astrophysical plasma environments including blazar jets[Reference Begelman, Ergun and Rees3, Reference Bingham, Kellett, Cairns, Tonge and Mendonca4, Reference Bamford, Kellett, Bradford, Norberg, Thornton, Gibson, Crawford, Silva, Gargat é and Bingham19, Reference Bamford, Alves, Cruz, Kellett, Fonseca, O Silva, Trines, Halekas, Kramer and Harnett20, Reference Bingham, Speirs, Kellett, Vorgul, McConville, Cairns, Cross, Phelps and Ronald47].
Acknowledgements
The research leading to the results in this article has received funding from the Engineering and Physical Sciences Research Council (grant Nos. EP/N014472/1, EP/R004773/1 and EP/N013298/1) and the Science and Technologies Facilities Council of the United Kingdom. F.C. and L.O.S. acknowledge support from the European Research Council (InPairs ERC-2015-AdG 695088) and FCT Portugal (grant No. PD/BD/114307/2016). This work was supported in part at the University of Chicago by the US DOE NNSA ASC through the Argonne Institute for Computing in Science under FWP 57789 and the US DOE Office of Science through grant No. DE- SC0016566.