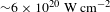1 Introduction
The interaction of ultraintense laser pulses (![]() ${>}10^{18}~\text{W}~\text{cm}^{-2}$) with thin foil targets (nanometre–micrometre scale thickness) results in the generation of high energy ion beams[Reference Daido, Nishiuchi and Pirozhkov1, Reference Macchi, Borghesi and Passoni2], bright x-ray sources[Reference Faenov, Colgan, Hansen, Zhidkov, Pikuz, Nishiuchi, Pikuz, Skobelev, Abdallah, Sakaki, Sagisaka, Pirozhkov, Ogura, Fukuda, Kanasaki, Hasegawa, Nishikino, Kando, Watanabe, Kawachi, Masuda, Hosokai, Kodama and Kondo3, Reference Colgan, Abdallah, Faenov, Pikuz, Wagenaars, Booth, Culfa, Dance, Evans, Gray, Kaempfer, Lancaster, McKenna, Rossall, Skobelev, Schulze, Uschmann, Zhidkov and Woolsey4] or in the production of high harmonics[Reference Dromey, Rykovanov, Yeung, Hörlein, Jung, Gautier, Dzelzainis, Kiefer, Palaniyppan, Shah, Schreiber, Ruhl, Fernandez, Lewis, Zepf and Hegelich5]. The basis of the underlying physics of all these laser–plasma sources is the collective response of the plasma electrons to the intense laser light. The electrons are directly accelerated by the laser electric and magnetic fields, which in turn exhibit distinct characteristics depending on the polarization. Therefore, the role of polarization in the collective dynamics of electrons in ultraintense laser pulse interactions with thin foil targets is both of fundamental interest and potentially important for controlling the production of secondary particles and radiation.
${>}10^{18}~\text{W}~\text{cm}^{-2}$) with thin foil targets (nanometre–micrometre scale thickness) results in the generation of high energy ion beams[Reference Daido, Nishiuchi and Pirozhkov1, Reference Macchi, Borghesi and Passoni2], bright x-ray sources[Reference Faenov, Colgan, Hansen, Zhidkov, Pikuz, Nishiuchi, Pikuz, Skobelev, Abdallah, Sakaki, Sagisaka, Pirozhkov, Ogura, Fukuda, Kanasaki, Hasegawa, Nishikino, Kando, Watanabe, Kawachi, Masuda, Hosokai, Kodama and Kondo3, Reference Colgan, Abdallah, Faenov, Pikuz, Wagenaars, Booth, Culfa, Dance, Evans, Gray, Kaempfer, Lancaster, McKenna, Rossall, Skobelev, Schulze, Uschmann, Zhidkov and Woolsey4] or in the production of high harmonics[Reference Dromey, Rykovanov, Yeung, Hörlein, Jung, Gautier, Dzelzainis, Kiefer, Palaniyppan, Shah, Schreiber, Ruhl, Fernandez, Lewis, Zepf and Hegelich5]. The basis of the underlying physics of all these laser–plasma sources is the collective response of the plasma electrons to the intense laser light. The electrons are directly accelerated by the laser electric and magnetic fields, which in turn exhibit distinct characteristics depending on the polarization. Therefore, the role of polarization in the collective dynamics of electrons in ultraintense laser pulse interactions with thin foil targets is both of fundamental interest and potentially important for controlling the production of secondary particles and radiation.
At laser intensities above the relativistic threshold (i.e., where the quiver energy of an electron exceeds its rest mass energy) the force on the electrons arising from the ![]() $\boldsymbol{v}\times \boldsymbol{B}$ term in the Lorentz equation is of the same order as that due to the electric field. The ponderomotive force with this additional term included can be expressed as[Reference Kruer and Estabrook6–Reference Macchi8]:
$\boldsymbol{v}\times \boldsymbol{B}$ term in the Lorentz equation is of the same order as that due to the electric field. The ponderomotive force with this additional term included can be expressed as[Reference Kruer and Estabrook6–Reference Macchi8]:
where ![]() $e$ is the electron charge,
$e$ is the electron charge, ![]() $m_{e}$ the electron rest mass,
$m_{e}$ the electron rest mass, ![]() $\unicode[STIX]{x1D714}$ the laser angular frequency and
$\unicode[STIX]{x1D714}$ the laser angular frequency and ![]() $\unicode[STIX]{x1D716}$ is the laser polarization ellipticity (
$\unicode[STIX]{x1D716}$ is the laser polarization ellipticity (![]() $0<\unicode[STIX]{x1D716}<1$). The first term on the right drives electrons from regions of higher to lower electric fields at a constant rate. The second term is the
$0<\unicode[STIX]{x1D716}<1$). The first term on the right drives electrons from regions of higher to lower electric fields at a constant rate. The second term is the ![]() $\boldsymbol{J}\times \boldsymbol{B}$ heating mechanism and induces electron oscillation at twice the laser frequency (
$\boldsymbol{J}\times \boldsymbol{B}$ heating mechanism and induces electron oscillation at twice the laser frequency (![]() $2\unicode[STIX]{x1D714}$). For linearly polarized pulses
$2\unicode[STIX]{x1D714}$). For linearly polarized pulses ![]() $\unicode[STIX]{x1D716}=0$, which maximizes the heating component in Equation (1). For circular polarization
$\unicode[STIX]{x1D716}=0$, which maximizes the heating component in Equation (1). For circular polarization ![]() $\unicode[STIX]{x1D716}=1$, which makes the
$\unicode[STIX]{x1D716}=1$, which makes the ![]() $\boldsymbol{J}\times \boldsymbol{B}$ heating component vanish. For a mid-range laser polarization ellipticity, i.e.,
$\boldsymbol{J}\times \boldsymbol{B}$ heating component vanish. For a mid-range laser polarization ellipticity, i.e., ![]() $\unicode[STIX]{x1D716}=0.5$, the ellipticity factor
$\unicode[STIX]{x1D716}=0.5$, the ellipticity factor ![]() $(1-\unicode[STIX]{x1D716}^{2})/(1+\unicode[STIX]{x1D716}^{2})$ is equal to 0.6, which induces a degree of electron heating which is closer to the case of linear than circular polarization. Laser polarization is thus highly important in defining the coupling of laser energy to target plasma electrons at relativistic laser intensities. The degree of target-electron heating in turn determines whether the plasma thermal pressure dominates over laser radiation pressure. For this reason circular polarization has been shown to be preferable for the optimization of laser radiation pressure acceleration (RPA)[Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou9, Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima10].
$(1-\unicode[STIX]{x1D716}^{2})/(1+\unicode[STIX]{x1D716}^{2})$ is equal to 0.6, which induces a degree of electron heating which is closer to the case of linear than circular polarization. Laser polarization is thus highly important in defining the coupling of laser energy to target plasma electrons at relativistic laser intensities. The degree of target-electron heating in turn determines whether the plasma thermal pressure dominates over laser radiation pressure. For this reason circular polarization has been shown to be preferable for the optimization of laser radiation pressure acceleration (RPA)[Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou9, Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima10].

Figure 1. (a)–(d) Electron density and laser intensity from a 2D PIC simulation employing circularly polarized light, for target thickness: (a) ![]() $l=500~\text{nm}$; (b)
$l=500~\text{nm}$; (b) ![]() $l=200~\text{nm}$; (c)
$l=200~\text{nm}$; (c) ![]() $l=40~\text{nm}$; (d)
$l=40~\text{nm}$; (d) ![]() $l=10~\text{nm}$. All figures are at the same time step, corresponding to the moment that the
$l=10~\text{nm}$. All figures are at the same time step, corresponding to the moment that the ![]() $l=10~\text{nm}$ target becomes relativistically transparent.
$l=10~\text{nm}$ target becomes relativistically transparent.
Generally, the laser interaction with the plasma electrons becomes more volumetric as the target thickness is decreased down to the scale of tens to hundreds of nanometres. To illustrate this, Figure 1 shows results from 2D particle-in-cell (PIC) simulations where circularly polarized light is incident upon aluminium (Al) foil targets with thicknesses: ![]() $l=500$, 200, 40 and 10 nm. The laser intensity is overlaid with the electron density. These four cases illustrate how the laser pulse interaction changes with target thickness. For the
$l=500$, 200, 40 and 10 nm. The laser intensity is overlaid with the electron density. These four cases illustrate how the laser pulse interaction changes with target thickness. For the ![]() $l=500~\text{nm}$ and
$l=500~\text{nm}$ and ![]() $l=200~\text{nm}$ cases the laser produces radiation pressure induced hole boring[Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou9, Reference Kodama, Takahashi, Tanaka, Tsukamoto, Hashimoto, Kato and Mima11] into the target. This results in the electron density at the front of the laser pulse being compressed. When the target thickness is decreased to 40 nm a section of the target foil near the peak of the laser intensity is driven forward as a whole, in what is termed the Light Sail mode[Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima10, Reference Macchi, Veghini and Pegoraro12] of RPA. This mode is expected to produce high ion energies and fast scaling with laser intensity[Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely, Osterholz, Prasad, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi13]. As the thickness is decreased further, the target can become transparent to the laser light during the interaction. At the laser intensities achievable with present state-of-the-art lasers, this typically occurs due to a combination of the expansion of the heated target-electron population and a relativistic increase in the electron mass by the Lorentz factor,
$l=200~\text{nm}$ cases the laser produces radiation pressure induced hole boring[Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou9, Reference Kodama, Takahashi, Tanaka, Tsukamoto, Hashimoto, Kato and Mima11] into the target. This results in the electron density at the front of the laser pulse being compressed. When the target thickness is decreased to 40 nm a section of the target foil near the peak of the laser intensity is driven forward as a whole, in what is termed the Light Sail mode[Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima10, Reference Macchi, Veghini and Pegoraro12] of RPA. This mode is expected to produce high ion energies and fast scaling with laser intensity[Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely, Osterholz, Prasad, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi13]. As the thickness is decreased further, the target can become transparent to the laser light during the interaction. At the laser intensities achievable with present state-of-the-art lasers, this typically occurs due to a combination of the expansion of the heated target-electron population and a relativistic increase in the electron mass by the Lorentz factor, ![]() $\unicode[STIX]{x1D6FE}$. The latter process increases the relativistically corrected plasma critical density:
$\unicode[STIX]{x1D6FE}$. The latter process increases the relativistically corrected plasma critical density:
where ![]() $\unicode[STIX]{x1D700}_{0}$ is the vacuum permittivity.
$\unicode[STIX]{x1D700}_{0}$ is the vacuum permittivity.
If the plasma electron density is greater than the relativistically corrected density (i.e., ![]() $n_{e}>n_{c}^{\prime }$), then the plasma will remain opaque throughout the interaction. If, however, the degree of electron heating is large enough that the condition
$n_{e}>n_{c}^{\prime }$), then the plasma will remain opaque throughout the interaction. If, however, the degree of electron heating is large enough that the condition ![]() $n_{e}<n_{c}^{\prime }$ is satisfied, then the plasma becomes relativistically underdense, through a phenomenon known as relativistically induced transparency (RIT), enabling the remainder of the laser pulse to propagate through. Although this principle holds for all target thicknesses, more detailed models have been developed to take into account additional phenomena affecting the onset of transparency in targets with thickness below the laser wavelength. A 1D model has been included in several references[Reference Macchi, Veghini and Pegoraro12, Reference Vshivkov14, Reference Bulanov, Schroeder, Esarey and Leemans15], which, assuming a Dirac delta-like density profile for the target and calculating analytically the nonlinear transmission and reflection coefficients, results in a transparency threshold for thin foils and ultraintense (
$n_{e}<n_{c}^{\prime }$ is satisfied, then the plasma becomes relativistically underdense, through a phenomenon known as relativistically induced transparency (RIT), enabling the remainder of the laser pulse to propagate through. Although this principle holds for all target thicknesses, more detailed models have been developed to take into account additional phenomena affecting the onset of transparency in targets with thickness below the laser wavelength. A 1D model has been included in several references[Reference Macchi, Veghini and Pegoraro12, Reference Vshivkov14, Reference Bulanov, Schroeder, Esarey and Leemans15], which, assuming a Dirac delta-like density profile for the target and calculating analytically the nonlinear transmission and reflection coefficients, results in a transparency threshold for thin foils and ultraintense (![]() $a_{0}\gg 1$) laser pulses as:
$a_{0}\gg 1$) laser pulses as:
where ![]() $l$ is the target thickness. As
$l$ is the target thickness. As ![]() $n_{c}$ and
$n_{c}$ and ![]() $\unicode[STIX]{x1D706}$ are intrinsic parameters of the laser, the effective parameter which determines the onset of relativistic transparency in ultrathin targets is the areal density,
$\unicode[STIX]{x1D706}$ are intrinsic parameters of the laser, the effective parameter which determines the onset of relativistic transparency in ultrathin targets is the areal density, ![]() $n_{e}l$.
$n_{e}l$.
We have recently reported on the collective response of target electrons to intense laser light in ultrathin targets for which significant hole boring occurs, in the near-critical density regime[Reference Gray, MacLellan, Gonzalez-Izquierdo, Powell, Carroll, Murphy, Stockhausen, Rusby, Scott, Wilson, Booth, Symes, Hawkes, Torres, Borghesi, Neely and McKenna16–Reference Gonzalez-Izquierdo, Gray, King, Dance, Wilson, McCreadie, Butler, Capdessus, Hawkes, Green, Borghesi, Neely and McKenna19]. Using picosecond duration laser pulses and ultrathin Al targets, Powell et al. [Reference Powell, King, Gray, MacLellan, Gonzalez-Izquierdo, Stockhausen, Hicks, Dover, Rusby, Carroll, Padda, Torres, Kar, Clarke, Musgrave, Najmudin, Borghesi, Neely and McKenna17] demonstrated that the onset of transparency can produce a directed jet of energetic electrons in the expanding plasma. For shorter (![]() ${\sim}40~\text{fs}$) pulses, it is shown by Gray et al. [Reference Gray, MacLellan, Gonzalez-Izquierdo, Powell, Carroll, Murphy, Stockhausen, Rusby, Scott, Wilson, Booth, Symes, Hawkes, Torres, Borghesi, Neely and McKenna16] that in the case of targets with thickness on the threshold for transparency, the electron beam distribution becomes elliptical, with the major axis of the ellipse determined by the laser polarization direction. Focusing on thinner targets, Gonzalez-Izquierdo et al. [Reference Gonzalez-Izquierdo, Gray, King, Dance, Wilson, McCreadie, Butler, Capdessus, Hawkes, Green, Borghesi, Neely and McKenna19] showed that a relativistic plasma aperture produced during transparency induces diffraction of the transmitted laser light. The resulting spatial modification of the electron beam is shown to be sensitive to the degree of ellipticity of the polarization. In this paper, we present additional experimental and simulation results which support our earlier conclusions on the effects of laser polarization on collective electron dynamics in ultrathin foil targets. Measurements of the spatial-intensity distribution of the beam of relativistic electrons produced with linear, elliptical and circular polarization, and for foil thicknesses on either side of the transparency threshold, are compared. It is shown that laser polarization provides a mechanism by which the collective plasma electron motion can potentially be controlled.
${\sim}40~\text{fs}$) pulses, it is shown by Gray et al. [Reference Gray, MacLellan, Gonzalez-Izquierdo, Powell, Carroll, Murphy, Stockhausen, Rusby, Scott, Wilson, Booth, Symes, Hawkes, Torres, Borghesi, Neely and McKenna16] that in the case of targets with thickness on the threshold for transparency, the electron beam distribution becomes elliptical, with the major axis of the ellipse determined by the laser polarization direction. Focusing on thinner targets, Gonzalez-Izquierdo et al. [Reference Gonzalez-Izquierdo, Gray, King, Dance, Wilson, McCreadie, Butler, Capdessus, Hawkes, Green, Borghesi, Neely and McKenna19] showed that a relativistic plasma aperture produced during transparency induces diffraction of the transmitted laser light. The resulting spatial modification of the electron beam is shown to be sensitive to the degree of ellipticity of the polarization. In this paper, we present additional experimental and simulation results which support our earlier conclusions on the effects of laser polarization on collective electron dynamics in ultrathin foil targets. Measurements of the spatial-intensity distribution of the beam of relativistic electrons produced with linear, elliptical and circular polarization, and for foil thicknesses on either side of the transparency threshold, are compared. It is shown that laser polarization provides a mechanism by which the collective plasma electron motion can potentially be controlled.
2 Experimental arrangement and results
The experiment was performed using the Gemini laser, at the Rutherford Appleton Laboratory, which delivers pulses of ![]() ${\sim}40~\text{fs}$ (FWHM) in duration and
${\sim}40~\text{fs}$ (FWHM) in duration and ![]() ${\sim}800~\text{nm}$ of central wavelength,
${\sim}800~\text{nm}$ of central wavelength, ![]() $\unicode[STIX]{x1D706}$. A schematic of the beam layout in the target chamber is shown in Figure 2(a). The incoming beam is reflected by a double plasma mirror[Reference Dromey, Kar, Zepf and Foster20] in order to increase the pulse temporal intensity contrast to
$\unicode[STIX]{x1D706}$. A schematic of the beam layout in the target chamber is shown in Figure 2(a). The incoming beam is reflected by a double plasma mirror[Reference Dromey, Kar, Zepf and Foster20] in order to increase the pulse temporal intensity contrast to ![]() ${\sim}10^{9}$ at 5 ps and
${\sim}10^{9}$ at 5 ps and ![]() ${\sim}10^{11}$ at 1 ns prior to the peak of the pulse. At the output of the plasma mirror system an adaptive optic mirror (not included in Figure 2) was used to minimize aberrations of the laser wavefront and thus produce a high quality focal spot on the target. The laser beam was also passed through either a
${\sim}10^{11}$ at 1 ns prior to the peak of the pulse. At the output of the plasma mirror system an adaptive optic mirror (not included in Figure 2) was used to minimize aberrations of the laser wavefront and thus produce a high quality focal spot on the target. The laser beam was also passed through either a ![]() $\unicode[STIX]{x1D706}/2$ or
$\unicode[STIX]{x1D706}/2$ or ![]() $\unicode[STIX]{x1D706}/4$ wave plate to control the beam polarization. Four polarization cases were employed using the
$\unicode[STIX]{x1D706}/4$ wave plate to control the beam polarization. Four polarization cases were employed using the ![]() $\unicode[STIX]{x1D706}/4$ wave plate: linear polarization along the
$\unicode[STIX]{x1D706}/4$ wave plate: linear polarization along the ![]() $Y$-axis (
$Y$-axis (![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=0$), elliptical (
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=0$), elliptical (![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/4$ and
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/4$ and ![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D70B}/4$) and circular (
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D70B}/4$) and circular (![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/2$), where
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/2$), where ![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}$ is the phase difference between the two orthogonal electric field components of the laser beam. Alternatively, the
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}$ is the phase difference between the two orthogonal electric field components of the laser beam. Alternatively, the ![]() $\unicode[STIX]{x1D706}/2$ wave plate was used to produce a linear polarization along the
$\unicode[STIX]{x1D706}/2$ wave plate was used to produce a linear polarization along the ![]() $Z$-axis (
$Z$-axis (![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}$). The beam was then directed onto an
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}$). The beam was then directed onto an ![]() $F/2$ off-axis parabolic mirror, which focused it along the target normal to a spot with diameter equal to
$F/2$ off-axis parabolic mirror, which focused it along the target normal to a spot with diameter equal to ![]() $3~\unicode[STIX]{x03BC}\text{m}$ (FWHM). A total laser energy of
$3~\unicode[STIX]{x03BC}\text{m}$ (FWHM). A total laser energy of ![]() ${\sim}4.6$ J reaching the target was measured using a calorimeter. For the measured laser focal spot,
${\sim}4.6$ J reaching the target was measured using a calorimeter. For the measured laser focal spot, ![]() ${\sim}2$ J was contained within the FWHM (
${\sim}2$ J was contained within the FWHM (![]() $3~\unicode[STIX]{x03BC}\text{m}$), resulting in a calculated peak intensity of
$3~\unicode[STIX]{x03BC}\text{m}$), resulting in a calculated peak intensity of ![]() $6\times 10^{20}~\text{W}~\text{cm}^{-2}$. Planar aluminium target foils with thickness,
$6\times 10^{20}~\text{W}~\text{cm}^{-2}$. Planar aluminium target foils with thickness, ![]() $l$, equal to 10, 40 and 800 nm were employed.
$l$, equal to 10, 40 and 800 nm were employed.

Figure 2. (a) Layout of the laser beam path in the target chamber. The laser intensity contrast is increased using a double plasma mirror. Wave plates are inserted before focusing to vary the laser polarization. (b) Schematic showing the position of the IP stack detector used to measure the electron spatial-intensity distribution.

Figure 3. Measured electron density distribution. (a–d) Electron density as measured using IP for ![]() $l=800~\text{nm}$, for electrons with energy greater than: (a) 3.5 MeV; (b) 5.8 MeV; (c) 10.3 MeV; and (d) 17.0 MeV; all for linear polarization in the
$l=800~\text{nm}$, for electrons with energy greater than: (a) 3.5 MeV; (b) 5.8 MeV; (c) 10.3 MeV; and (d) 17.0 MeV; all for linear polarization in the ![]() $Y$-axis. (e–h) Same for
$Y$-axis. (e–h) Same for ![]() $l=40~\text{nm}$ and linear polarization in the
$l=40~\text{nm}$ and linear polarization in the ![]() $Y$-axis. (i–l) Same for
$Y$-axis. (i–l) Same for ![]() $l=40~\text{nm}$ and linear polarization in the
$l=40~\text{nm}$ and linear polarization in the ![]() $Z$-axis. The colour maps are scaled by the stated value
$Z$-axis. The colour maps are scaled by the stated value ![]() $F$ to clearly show the features of interest at each energy slice. The red arrows show the laser polarization.
$F$ to clearly show the features of interest at each energy slice. The red arrows show the laser polarization.
The spatial-intensity distribution of the beam of relativistic electrons escaping from the target was measured in coarse energy steps using stacked imaging plate (IP) and Fe filters. The detector stack was positioned 3.4 cm downstream centred on the laser axis, as shown in Figure 2(b).
2.1 The radiation pressure dominant regime
We start by considering the case in which the target remains opaque during the whole interaction for the laser pulse parameters considered. Measurements of the transmitted laser light as a function of ![]() $l$, reported in Ref. [Reference Gray, MacLellan, Gonzalez-Izquierdo, Powell, Carroll, Murphy, Stockhausen, Rusby, Scott, Wilson, Booth, Symes, Hawkes, Torres, Borghesi, Neely and McKenna16], show that, under the conditions of the experiment, this case is obtained for target thickness
$l$, reported in Ref. [Reference Gray, MacLellan, Gonzalez-Izquierdo, Powell, Carroll, Murphy, Stockhausen, Rusby, Scott, Wilson, Booth, Symes, Hawkes, Torres, Borghesi, Neely and McKenna16], show that, under the conditions of the experiment, this case is obtained for target thickness ![]() $l\geqslant 40~\text{nm}$. Figure 3 shows time-integrated measurements of the electron spatial-intensity distributions above given energy thresholds, measured in the
$l\geqslant 40~\text{nm}$. Figure 3 shows time-integrated measurements of the electron spatial-intensity distributions above given energy thresholds, measured in the ![]() $Y$–
$Y$–![]() $Z$ plane for linearly polarized light. The colour maps are scaled by the stated value of
$Z$ plane for linearly polarized light. The colour maps are scaled by the stated value of ![]() $F$ to clearly show the features of interest at each energy. For
$F$ to clearly show the features of interest at each energy. For ![]() $l=800~\text{nm}$, the high density region of the electron beam is approximately circular, with a low density halo stretched in the polarization direction, as shown in Figures 3(a–d). When the target thickness is decreased to 40 nm, for which the target still remains opaque, but close to the transparency threshold, significant radiation pressure and interaction over the target volume occurs. Under these conditions the electron beam has an elliptical distribution, with the major axis of the ellipse aligned along the direction of the laser polarization, as illustrated in Figures 3(e–h). When the direction of the plane of polarization is rotated by
$l=800~\text{nm}$, the high density region of the electron beam is approximately circular, with a low density halo stretched in the polarization direction, as shown in Figures 3(a–d). When the target thickness is decreased to 40 nm, for which the target still remains opaque, but close to the transparency threshold, significant radiation pressure and interaction over the target volume occurs. Under these conditions the electron beam has an elliptical distribution, with the major axis of the ellipse aligned along the direction of the laser polarization, as illustrated in Figures 3(e–h). When the direction of the plane of polarization is rotated by ![]() $90^{\circ }$, the electron beam continues to exhibit an elliptical distribution, but with the major axis of the ellipse rotated similarly (compare Figures 3(e–h) and 3(i–l)). The sensitivity of the ellipticity of the accelerated electron beam to laser polarization indicates a strong electron interaction with the laser field when the target is at near-critical (but still opaque) densities over the full laser pulse interaction. Electrons are effectively swept from side to side by the oscillating electric field of the laser light, which propagates deep into the target.
$90^{\circ }$, the electron beam continues to exhibit an elliptical distribution, but with the major axis of the ellipse rotated similarly (compare Figures 3(e–h) and 3(i–l)). The sensitivity of the ellipticity of the accelerated electron beam to laser polarization indicates a strong electron interaction with the laser field when the target is at near-critical (but still opaque) densities over the full laser pulse interaction. Electrons are effectively swept from side to side by the oscillating electric field of the laser light, which propagates deep into the target.
An additional experimental verification of the influence of laser polarization on the collective electron motion for ![]() $l=40$ nm was performed using elliptical and circular laser polarizations. Figures 4(a–d) and 4(e–h), show the results for two elliptical cases with
$l=40$ nm was performed using elliptical and circular laser polarizations. Figures 4(a–d) and 4(e–h), show the results for two elliptical cases with ![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/4$ and
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/4$ and ![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D70B}/4$, respectively. The electron beam also exhibits a clear elliptical distribution, with the major axis of the ellipse parallel to the ‘average’ polarization axis. By contrast, a circular electron beam distribution is produced employing circularly polarized light, as shown in Figures 4(i–l). This is consistent with a strong interaction of electrons with laser electric field and laser radiation pressure.
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D70B}/4$, respectively. The electron beam also exhibits a clear elliptical distribution, with the major axis of the ellipse parallel to the ‘average’ polarization axis. By contrast, a circular electron beam distribution is produced employing circularly polarized light, as shown in Figures 4(i–l). This is consistent with a strong interaction of electrons with laser electric field and laser radiation pressure.

Figure 4. Measured electron density distribution. (a–d) Electron density as measured using IP for ![]() $l=40~\text{nm}$, for electrons with energy greater than: (a) 3.5 MeV; (b) 5.8 MeV; (c) 10.3 MeV; and (d) 17.0 MeV; all for elliptical polarization (
$l=40~\text{nm}$, for electrons with energy greater than: (a) 3.5 MeV; (b) 5.8 MeV; (c) 10.3 MeV; and (d) 17.0 MeV; all for elliptical polarization (![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/4$). (e–h) Same for elliptical polarization (
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/4$). (e–h) Same for elliptical polarization (![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D70B}/4$). (i–l) Same for circular polarization (
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D70B}/4$). (i–l) Same for circular polarization (![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/2$). The colour maps are scaled by the stated value
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/2$). The colour maps are scaled by the stated value ![]() $F$ to clearly show the features of interest at each energy slice. The red arrows show the laser polarization.
$F$ to clearly show the features of interest at each energy slice. The red arrows show the laser polarization.
The complete set of ![]() $l=40~\text{nm}$ measurements indicate that the target electrons are responding collectively to the laser polarization. These results highlight the potential to manipulate collective electron motion in near-critical density plasma, for which there is significant interaction with the laser electric field over the target volume.
$l=40~\text{nm}$ measurements indicate that the target electrons are responding collectively to the laser polarization. These results highlight the potential to manipulate collective electron motion in near-critical density plasma, for which there is significant interaction with the laser electric field over the target volume.
2.2 The relativistically transparency dominant regime
For the laser characteristics considered in this study, the target becomes relativistically transparent for thicknesses ![]() ${<}40~\text{nm}$ (as reported in Ref. [Reference Gray, MacLellan, Gonzalez-Izquierdo, Powell, Carroll, Murphy, Stockhausen, Rusby, Scott, Wilson, Booth, Symes, Hawkes, Torres, Borghesi, Neely and McKenna16]). The highest degree of transparency was found for the thinnest target investigated, i.e.,
${<}40~\text{nm}$ (as reported in Ref. [Reference Gray, MacLellan, Gonzalez-Izquierdo, Powell, Carroll, Murphy, Stockhausen, Rusby, Scott, Wilson, Booth, Symes, Hawkes, Torres, Borghesi, Neely and McKenna16]). The highest degree of transparency was found for the thinnest target investigated, i.e., ![]() $l=10~\text{nm}$. The most salient results for all three polarization cases of the collective electron motion investigation for this target undergoing significant relativistic transparency are shown in Figures 5(a–c). A more detailed analysis of these results are reported in Gonzalez-Izquierdo et al. [Reference Gonzalez-Izquierdo, Gray, King, Dance, Wilson, McCreadie, Butler, Capdessus, Hawkes, Green, Borghesi, Neely and McKenna19]. A double-lobe distribution in the electron density is measured in the case of linearly polarized light, with the axis separating the lobes orientated perpendicular to the laser polarization axis (Figure 5(a)). The electron distribution is also double-lobed for the case of elliptically polarized light, with the axis separating the lobes orientated perpendicular to the ‘average’ polarization axis (Figure 5(b)). The measurement for circularly polarized light, displayed in Figure 5(c), also exhibits a double-lobe structure, but with a smaller lobe separation and a lower density halo at larger radii and
$l=10~\text{nm}$. The most salient results for all three polarization cases of the collective electron motion investigation for this target undergoing significant relativistic transparency are shown in Figures 5(a–c). A more detailed analysis of these results are reported in Gonzalez-Izquierdo et al. [Reference Gonzalez-Izquierdo, Gray, King, Dance, Wilson, McCreadie, Butler, Capdessus, Hawkes, Green, Borghesi, Neely and McKenna19]. A double-lobe distribution in the electron density is measured in the case of linearly polarized light, with the axis separating the lobes orientated perpendicular to the laser polarization axis (Figure 5(a)). The electron distribution is also double-lobed for the case of elliptically polarized light, with the axis separating the lobes orientated perpendicular to the ‘average’ polarization axis (Figure 5(b)). The measurement for circularly polarized light, displayed in Figure 5(c), also exhibits a double-lobe structure, but with a smaller lobe separation and a lower density halo at larger radii and ![]() $\unicode[STIX]{x1D70B}/2$ out of phase. The collective electron dynamics and role of polarization during the onset of transparency is clearly more complex than the case of radiation pressure into an opaque target.
$\unicode[STIX]{x1D70B}/2$ out of phase. The collective electron dynamics and role of polarization during the onset of transparency is clearly more complex than the case of radiation pressure into an opaque target.

Figure 5. (a) Electron density for a ![]() $l=10~\text{nm}$ target as measured using IP for electrons with energy greater than 3.5 MeV for linear polarization. (b) Same for elliptical polarization. (c) Same for circular polarization. (d) Same as (a) but for a
$l=10~\text{nm}$ target as measured using IP for electrons with energy greater than 3.5 MeV for linear polarization. (b) Same for elliptical polarization. (c) Same for circular polarization. (d) Same as (a) but for a ![]() $l=40~\text{nm}$ target with energy greater than 10.3 MeV. (e)–(g) 3D PIC simulation results for the electron density distribution from
$l=40~\text{nm}$ target with energy greater than 10.3 MeV. (e)–(g) 3D PIC simulation results for the electron density distribution from ![]() $l=10~\text{nm}$ and energies
$l=10~\text{nm}$ and energies ![]() $2<E<8$ MeV for linear, elliptical and circular polarization, respectively. (h) Same but from
$2<E<8$ MeV for linear, elliptical and circular polarization, respectively. (h) Same but from ![]() $l=40~\text{nm}$ and energies
$l=40~\text{nm}$ and energies ![]() $10<E<15$ MeV and linearly polarized light. The red arrows show the laser polarization.
$10<E<15$ MeV and linearly polarized light. The red arrows show the laser polarization.
3 PIC simulation results
3D PIC simulations were performed to elucidate the collective electron response to the laser light for 10 nm targets, for which significant RIT was measured experimentally, and ![]() $l=40~\text{nm}$ targets, which remained opaque throughout the laser–foil interaction, but sit close to the transparency threshold for the considered laser parameters.
$l=40~\text{nm}$ targets, which remained opaque throughout the laser–foil interaction, but sit close to the transparency threshold for the considered laser parameters.
The fully relativistic code EPOCH[Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers21] was used. A box of ![]() $20~\unicode[STIX]{x03BC}\text{m}\times 20~\unicode[STIX]{x03BC}\text{m}\times 20~\unicode[STIX]{x03BC}\text{m}$ with
$20~\unicode[STIX]{x03BC}\text{m}\times 20~\unicode[STIX]{x03BC}\text{m}\times 20~\unicode[STIX]{x03BC}\text{m}$ with ![]() $1000\times 720\times 720$ computational mesh cells was defined. The pulse had a Gaussian temporal and spatial profile with 40 fs width (FWHM) in time and
$1000\times 720\times 720$ computational mesh cells was defined. The pulse had a Gaussian temporal and spatial profile with 40 fs width (FWHM) in time and ![]() $3~\unicode[STIX]{x03BC}\text{m}$ (FWHM) in space. The energy of the pulse was selected to obtain a peak laser intensity of
$3~\unicode[STIX]{x03BC}\text{m}$ (FWHM) in space. The energy of the pulse was selected to obtain a peak laser intensity of ![]() $6\times 10^{20}~\text{W}~\text{cm}^{-2}$ to match the experiment. The laser wavelength was 800 nm. Simulations were performed for linearly (p-polarization along
$6\times 10^{20}~\text{W}~\text{cm}^{-2}$ to match the experiment. The laser wavelength was 800 nm. Simulations were performed for linearly (p-polarization along ![]() $Y$-axis), elliptically (
$Y$-axis), elliptically (![]() $\unicode[STIX]{x1D70B}/4$ phase difference) and circularly polarized light. Two representative target thicknesses were used: a solid 10-nm-thick
$\unicode[STIX]{x1D70B}/4$ phase difference) and circularly polarized light. Two representative target thicknesses were used: a solid 10-nm-thick ![]() $\text{Al}^{13+}$ slab as a target becoming relativistically transparent and a solid 40-nm-thick
$\text{Al}^{13+}$ slab as a target becoming relativistically transparent and a solid 40-nm-thick ![]() $\text{Al}^{13+}$ slab as a target remaining opaque during the laser interaction. In both cases 6-nm-thick
$\text{Al}^{13+}$ slab as a target remaining opaque during the laser interaction. In both cases 6-nm-thick ![]() $\text{C}^{6+}$ and
$\text{C}^{6+}$ and ![]() $\text{H}^{+}$ mixed hydrocarbon layers (with the form
$\text{H}^{+}$ mixed hydrocarbon layers (with the form ![]() $\text{C}_{2}\text{H}_{6}$) on the front and rear surfaces were included. Due to high computational requirements the mesh cell size was 20 nm. The target then was pre-expanded to a Gaussian profile (with 245 nm FWHM for the 10 nm case and 980 nm FWHM for the 40 nm case) in order to have a sufficient number of cells across it to avoid self-heating and other numerical artefacts. The peak electron density was reduced accordingly in both cases to keep the same areal density as a non-pre-expanded target. Pre-expansion of this order, prior to the peak of the laser interaction, is expected based on plasma expansion estimates for the measured laser contrast. The ion density was initialized to neutralize the electrons using appropriate proportions of
$\text{C}_{2}\text{H}_{6}$) on the front and rear surfaces were included. Due to high computational requirements the mesh cell size was 20 nm. The target then was pre-expanded to a Gaussian profile (with 245 nm FWHM for the 10 nm case and 980 nm FWHM for the 40 nm case) in order to have a sufficient number of cells across it to avoid self-heating and other numerical artefacts. The peak electron density was reduced accordingly in both cases to keep the same areal density as a non-pre-expanded target. Pre-expansion of this order, prior to the peak of the laser interaction, is expected based on plasma expansion estimates for the measured laser contrast. The ion density was initialized to neutralize the electrons using appropriate proportions of ![]() $\text{Al}^{13+}$,
$\text{Al}^{13+}$, ![]() $\text{C}^{6+}$ and
$\text{C}^{6+}$ and ![]() $\text{H}^{+}$ ions. The initial electron temperature, 100 keV, was selected to be low enough to avoid artificial thermal induced effects, but high enough to resolve the Debye length as closely as possible. Initially there were 22 simulation particles per cell per species (total of
$\text{H}^{+}$ ions. The initial electron temperature, 100 keV, was selected to be low enough to avoid artificial thermal induced effects, but high enough to resolve the Debye length as closely as possible. Initially there were 22 simulation particles per cell per species (total of ![]() $3.11\times 10^{9}$ simulation particles).
$3.11\times 10^{9}$ simulation particles).

Figure 6. (a) 2D (![]() $X$–
$X$–![]() $Z$) slice in the
$Z$) slice in the ![]() $Y=0$ plane showing the electron density of a 10 nm target thickness overlaid with the laser intensity contour at three example time steps and linearly polarized light (
$Y=0$ plane showing the electron density of a 10 nm target thickness overlaid with the laser intensity contour at three example time steps and linearly polarized light (![]() $T=0$ corresponds to the time at which the laser peak interacts with the plasma). (b) Same for elliptical polarization showing the results in a 2D (
$T=0$ corresponds to the time at which the laser peak interacts with the plasma). (b) Same for elliptical polarization showing the results in a 2D (![]() $X$–
$X$–![]() $Z$) slice rotated
$Z$) slice rotated ![]() $45^{\circ }$ around the laser propagation axis. (c) Same as (b) for circular polarization. (d–f) 2D (
$45^{\circ }$ around the laser propagation axis. (c) Same as (b) for circular polarization. (d–f) 2D (![]() $Y$–
$Y$–![]() $Z$) plane showing laser light intensity and electron density integrated over
$Z$) plane showing laser light intensity and electron density integrated over ![]() $X=0.7{-}1.5~\unicode[STIX]{x03BC}\text{m}$ (corresponding to one laser wavelength in the region of the high density of electrons that are accelerated forward) for linear, elliptical and circular polarization, respectively and 10 nm target thickness. The hollow arrows illustrate the direction of the ponderomotive force arising from the gradients in laser intensity.
$X=0.7{-}1.5~\unicode[STIX]{x03BC}\text{m}$ (corresponding to one laser wavelength in the region of the high density of electrons that are accelerated forward) for linear, elliptical and circular polarization, respectively and 10 nm target thickness. The hollow arrows illustrate the direction of the ponderomotive force arising from the gradients in laser intensity.
In Figures 6(a–c) a time evolution is presented, corresponding to time steps before and after the onset of RIT, of the electron density (normalized to the critical density) overlaid with the contour of the laser intensity for a ![]() $l=10~\text{nm}$ target and for linear, elliptical and circular polarization.
$l=10~\text{nm}$ target and for linear, elliptical and circular polarization. ![]() $T=0~\text{fs}$ corresponds to the peak of the incident laser intensity profile interacting with the plasma. These results show that when the target becomes relativistically transparent a ‘relativistic plasma aperture’ is formed. As discussed in Ref. [Reference Gonzalez-Izquierdo, Gray, King, Dance, Wilson, McCreadie, Butler, Capdessus, Hawkes, Green, Borghesi, Neely and McKenna19], the laser pulse has an approximately Gaussian intensity profile at focus. Thus there exists a spatial variation in the local electron heating within the target. The highest electron quiver energy is produced on axis and thus the relativistic plasma aperture is produced with a diameter defined by the threshold intensity for relativistic transparency. For a typical laser focal spot of several times the laser wavelength, the aperture diameter will be of the order of a few times the wavelength. The light transmitted through this self-formed aperture is then spatially modulated following the diffraction phenomenon according to the Huygens–Fresnel principle[Reference Fresnel22, Reference Stratton and Chu23].
$T=0~\text{fs}$ corresponds to the peak of the incident laser intensity profile interacting with the plasma. These results show that when the target becomes relativistically transparent a ‘relativistic plasma aperture’ is formed. As discussed in Ref. [Reference Gonzalez-Izquierdo, Gray, King, Dance, Wilson, McCreadie, Butler, Capdessus, Hawkes, Green, Borghesi, Neely and McKenna19], the laser pulse has an approximately Gaussian intensity profile at focus. Thus there exists a spatial variation in the local electron heating within the target. The highest electron quiver energy is produced on axis and thus the relativistic plasma aperture is produced with a diameter defined by the threshold intensity for relativistic transparency. For a typical laser focal spot of several times the laser wavelength, the aperture diameter will be of the order of a few times the wavelength. The light transmitted through this self-formed aperture is then spatially modulated following the diffraction phenomenon according to the Huygens–Fresnel principle[Reference Fresnel22, Reference Stratton and Chu23].
In the linear polarization case, Figure 6(a) shows that when RIT occurs the accelerated electrons respond to the diffracted laser intensity distribution. At the ![]() $X$ position at which the electron density is highest on axis
$X$ position at which the electron density is highest on axis ![]() $(X\sim 1~\unicode[STIX]{x03BC}\text{m})$, the laser profile has a double diffraction lobe distribution orientated perpendicular to the polarization direction. The electrons in the region of the double diffraction lobe are subject to a transverse ponderomotive force in the plane of the target, as shown by the hollow arrows (from field mapping) as displayed in Figure 6(d). This drives the electrons into a double-lobe distribution, perpendicular to the laser polarization direction. A study of the angular velocity of the polarization vector and the magnitude of the electric field reveals that the laser electric field flips between the two lobes over each half-laser period. Therefore, once the plasma aperture is formed this instantaneous flip of the double-lobe electric field will remain until the end of the pulse reinforcing the ponderomotive generation of the electron distribution in a double lobe.
$(X\sim 1~\unicode[STIX]{x03BC}\text{m})$, the laser profile has a double diffraction lobe distribution orientated perpendicular to the polarization direction. The electrons in the region of the double diffraction lobe are subject to a transverse ponderomotive force in the plane of the target, as shown by the hollow arrows (from field mapping) as displayed in Figure 6(d). This drives the electrons into a double-lobe distribution, perpendicular to the laser polarization direction. A study of the angular velocity of the polarization vector and the magnitude of the electric field reveals that the laser electric field flips between the two lobes over each half-laser period. Therefore, once the plasma aperture is formed this instantaneous flip of the double-lobe electric field will remain until the end of the pulse reinforcing the ponderomotive generation of the electron distribution in a double lobe.
By contrast, circularly polarized light results in significantly less electron heating and expansion, allowing radiation pressure to act on the target for a significant fraction of the interaction time[Reference Scullion, Doria, Romagnani, Sgattoni, Naughton, Symes, McKenna, Macchi, Zepf, Kar and Borghesi24]. The onset of RIT occurs later in the interaction, resulting in a smaller aperture (![]() ${\sim}1.5~\unicode[STIX]{x03BC}\text{m}$ in diameter) compared to the linear polarization case (
${\sim}1.5~\unicode[STIX]{x03BC}\text{m}$ in diameter) compared to the linear polarization case (![]() ${\sim}3~\unicode[STIX]{x03BC}\text{m}$ in diameter), as is shown in Figure 6(c). As a result, the diffraction pattern from the circularly polarized laser light passing through the evolving relativistic plasma aperture exhibits a single lobe rotating in a helical-like structure. The rotating single-lobe diffraction pattern produces a ring-like distribution in the electron density, as shown in Figure 6(f). As in the linear case, these results can be explained by analysing the angular velocity of the polarization vector and the magnitude of the electric field. In the circular case, the field components produce a dynamic intensity profile which makes a complete rotation, at a constant angular velocity, around the laser propagation axis once per laser period.
${\sim}3~\unicode[STIX]{x03BC}\text{m}$ in diameter), as is shown in Figure 6(c). As a result, the diffraction pattern from the circularly polarized laser light passing through the evolving relativistic plasma aperture exhibits a single lobe rotating in a helical-like structure. The rotating single-lobe diffraction pattern produces a ring-like distribution in the electron density, as shown in Figure 6(f). As in the linear case, these results can be explained by analysing the angular velocity of the polarization vector and the magnitude of the electric field. In the circular case, the field components produce a dynamic intensity profile which makes a complete rotation, at a constant angular velocity, around the laser propagation axis once per laser period.
In the elliptical polarization case, since the ![]() $\boldsymbol{J}\times \boldsymbol{B}$ heating component of the ponderomotive force is still significantly high for a phase difference equal to
$\boldsymbol{J}\times \boldsymbol{B}$ heating component of the ponderomotive force is still significantly high for a phase difference equal to ![]() $\unicode[STIX]{x1D70B}/4$ (using an ellipticity of 0.5 in Equation (1)), the electrons are bounded to a higher heating and expansion when compared to the circular case. This results in the earlier onset of RIT compared to the circular polarization case and the generation of a relativistic plasma aperture with a diameter in the order of the linear polarization case, approximately
$\unicode[STIX]{x1D70B}/4$ (using an ellipticity of 0.5 in Equation (1)), the electrons are bounded to a higher heating and expansion when compared to the circular case. This results in the earlier onset of RIT compared to the circular polarization case and the generation of a relativistic plasma aperture with a diameter in the order of the linear polarization case, approximately ![]() $3~\unicode[STIX]{x03BC}\text{m}$. Thus a similar laser diffraction pattern is generated when the laser propagates through the plasma aperture, as shown in Figure 6(b). A spatial integration of the electron density and laser intensity after the target reveals that a double-lobe diffraction pattern is also generated, in a similar way as in the linear polarization case. However, when the laser is elliptically polarized light both the angular velocity of the polarization vector rotation and the laser electric field exhibit a periodic change along a laser period going from maximum to lower values. Moreover, when the angular velocity is at a maximum the electric field is minimal and vice versa. The singular dynamics of elliptically polarized light, and subsequent diffraction patterns, leads to a double-lobe ponderomotive response of the plasma electrons, perpendicular to the ‘average’ polarization direction. This is shown in Figure 6(e).
$3~\unicode[STIX]{x03BC}\text{m}$. Thus a similar laser diffraction pattern is generated when the laser propagates through the plasma aperture, as shown in Figure 6(b). A spatial integration of the electron density and laser intensity after the target reveals that a double-lobe diffraction pattern is also generated, in a similar way as in the linear polarization case. However, when the laser is elliptically polarized light both the angular velocity of the polarization vector rotation and the laser electric field exhibit a periodic change along a laser period going from maximum to lower values. Moreover, when the angular velocity is at a maximum the electric field is minimal and vice versa. The singular dynamics of elliptically polarized light, and subsequent diffraction patterns, leads to a double-lobe ponderomotive response of the plasma electrons, perpendicular to the ‘average’ polarization direction. This is shown in Figure 6(e).
The previous 2D electron density distributions presented in Figures 6(d–f), for the three laser polarizations investigated, were obtained via spatial integration of the electron density in a small region after the target. As the measured electron distribution is time-integrated, the simulation results are also time-integrated in order to enable a realistic comparison. Figures 5(e–g) show corresponding example results from the 3D EPOCH simulations, integrated over five laser cycles at the end of the pulse for linearly, elliptically and circularly polarized light, respectively. The simulation results reproduce the shape of the measured distributions in all three polarization cases. The measured double-lobe electron density feature matches the simulation predictions in terms of the angular separation of the lobes and their orientation with respect to the polarization axes for both the linear and elliptical cases. From the discussion above, the circularly polarized case might be expected to produce an electron density ring owing to the constant rotational velocity of the electric field. However, the simulations show that there is in fact a slight distortion in the polarization induced by the evolving plasma aperture, resulting in the ring-like distribution with localized maxima shown in Figure 5(g).
In Figure 5(h) the time-integrated electron density distribution from a 3D PIC simulation using linearly polarized light and a ![]() $l=40~\text{nm}$ target is presented. It also reproduces the global electron response measured experimentally (Figure 5(d)), exhibiting an elliptical distribution with the major axis along the laser polarization direction.
$l=40~\text{nm}$ target is presented. It also reproduces the global electron response measured experimentally (Figure 5(d)), exhibiting an elliptical distribution with the major axis along the laser polarization direction.
4 Conclusions
The collective response of plasma electrons in ultrathin foils to radiation pressure and the onset of RIT has been explored experimentally and by 3D simulations. For targets which expand to densities close to the relativistically corrected critical density (![]() $l=40~\text{nm}$ in the present study), for which radiation pressure is active for the duration of the interaction, the plasma electrons are swept from side to side in the plane of the linear polarization, resulting in an elliptical beam distribution, as first reported in Gray et al. [Reference Gray, MacLellan, Gonzalez-Izquierdo, Powell, Carroll, Murphy, Stockhausen, Rusby, Scott, Wilson, Booth, Symes, Hawkes, Torres, Borghesi, Neely and McKenna16]. New experimental results investigating the electron beam dynamics using two distinctive elliptical laser polarization with
$l=40~\text{nm}$ in the present study), for which radiation pressure is active for the duration of the interaction, the plasma electrons are swept from side to side in the plane of the linear polarization, resulting in an elliptical beam distribution, as first reported in Gray et al. [Reference Gray, MacLellan, Gonzalez-Izquierdo, Powell, Carroll, Murphy, Stockhausen, Rusby, Scott, Wilson, Booth, Symes, Hawkes, Torres, Borghesi, Neely and McKenna16]. New experimental results investigating the electron beam dynamics using two distinctive elliptical laser polarization with ![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/4$ and
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/4$ and ![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D70B}/4$ are presented. As in the linear polarization cases, when elliptically polarized light is used the accelerated plasma electrons exhibit a density distribution which is predominantly elliptical, with the major axis parallel to the major axis of the polarization direction. These results indicate a strong interaction between the electron and laser electric field for the laser conditions and this particular target thickness investigated.
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D70B}/4$ are presented. As in the linear polarization cases, when elliptically polarized light is used the accelerated plasma electrons exhibit a density distribution which is predominantly elliptical, with the major axis parallel to the major axis of the polarization direction. These results indicate a strong interaction between the electron and laser electric field for the laser conditions and this particular target thickness investigated.
By contrast, in the case of thinner targets, for which RIT occurs during the laser interaction (![]() $l=10~\text{nm}$ in the present study), the experimental results show singular electron beam distributions for each laser polarization investigated, linear, elliptical (
$l=10~\text{nm}$ in the present study), the experimental results show singular electron beam distributions for each laser polarization investigated, linear, elliptical (![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/4$) and circular. They change from a double-lobe distribution perpendicular to the laser polarization direction in the linear case, to a double-lobe structure perpendicular to the major axis for elliptical polarization and a ring-like distribution with localized maxima for circularly polarized laser light. An investigation with 3D PIC simulations reveals that this particular sensitivity of the electron distribution to the drive laser polarization in targets undergoing relativistic transparency arises from the near-field diffraction pattern in the intense laser light as it passes through a self-generated ‘relativistic plasma aperture’. It is observed that the plasma electrons collectively respond to the resulting near-field diffraction pattern.
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/4$) and circular. They change from a double-lobe distribution perpendicular to the laser polarization direction in the linear case, to a double-lobe structure perpendicular to the major axis for elliptical polarization and a ring-like distribution with localized maxima for circularly polarized laser light. An investigation with 3D PIC simulations reveals that this particular sensitivity of the electron distribution to the drive laser polarization in targets undergoing relativistic transparency arises from the near-field diffraction pattern in the intense laser light as it passes through a self-generated ‘relativistic plasma aperture’. It is observed that the plasma electrons collectively respond to the resulting near-field diffraction pattern.
These experimental and numerical results demonstrate that through suitable choice of target thickness and laser polarization, relativistic electron beams with distinctive spatial-intensity distributions can be generated. In this manner, modification of the laser polarization enables the potential to control the collective motion of electrons in plasma, which in turn can result in new approaches to manipulating ion acceleration[Reference Gonzalez-Izquierdo, King, Gray, Wilson, Dance, Powell, MacLellan, McCreadie, Butler, Hawkes, Green, Murphy, Stockhausen, Carroll, Booth, Scott, Borghesi, Neely and McKenna25] and secondary radiation production.
Acknowledgements
The authors thank the Gemini team at the Central Laser Facility of the Rutherford Appleton Laboratory for their support during the experiment. They acknowledge the use of the ARCHIE-WeST and ARCHER high performance computers. This work is supported by EPSRC (grants: EP/J003832/1, EP/M018091/1, EP/L001357/1, EP/K022415/1 and EP/L000237/1), STFC (grant number ST/K502340/1), the US Air Force Office of Scientific Research (grant: FA8655-13-1-3008) and the European Unions Horizon 2020 research and innovation programme (grant agreement No 654148 Laserlab-Europe). EPOCH was developed under EPSRC grant EP/G054940/1. Data associated with research published in this paper can be accessed at: http://dx.doi.org/10.15129/e92cfee7-a99c-4eee-8d94-0890027f36cf.