1 Introduction
Measuring magnetic fields in plasmas is vital for a proper understanding of plasma dynamics, but such measurements are often difficult to implement. Among the diagnostics commonly used in laser–plasma experiments[Reference Li, Séguin, Frenje, Rygg, Petrasso, Town, Amendt, Hatchett, Landen, Mackinnon, Patel, Smalyuk, Sangster and Knauer1–Reference Everson, Pribyl, Constantin, Zylstra, Schaeffer, Kugland and Niemann3], only proton radiography, in which (quasi) mono-energetic protons are deflected in the plasma by magnetic fields, has been used with some success at the OMEGA laser facility[Reference Li, Séguin, Frenje, Rygg, Petrasso, Town, Amendt, Hatchett, Landen, Mackinnon, Patel, Smalyuk, Sangster and Knauer1]. Proton radiography often allows a spatially resolved measurement of the magnetic field. While reconstruction of magnetic fields from proton radiography images is possible[Reference Bott, Graziani, Tzeferacos, White, Lamb, Gregori and Schekochihin4, Reference Kasim, Ceurvorst, Ratan, Sadler, Chen, Sävert, Trines, Bingham, Burrows, Kaluza and Norreys5], proton images are difficult to analyze, and the presence of caustic structures can make the reconstruction of the path-integrated magnetic field nonunique in the presence of strong fields. Moreover, this method cannot distinguish easily between magnetic or electric field deflections. This is particularly important in plasmas where strong electrostatic turbulence is present along with magnetic field fluctuations. Alternative diagnostics such as induction probes[Reference Meinecke, Tzeferacos, Bell, Bingham, Clarke, Churazov, Crowston, Doyle, Drake, Heathcote, Koenig, Kuramitsu, Kuranz, Lee, MacDonald, Murphy, Notley, Park, Pelka, Ravasio, Reville, Sakawa, Wan, Woolsey, Yurchak, Miniati, Schekochihin, Lamb and Gregori6, Reference Gregori, Reville and Miniati7] or polarimetry[Reference Davies, Haberberger, Boni, Ivancic, Brown and Froula8] have been attempted on OMEGA, but they are either too invasive or lack the needed sensitivity for accurate measurements.
Here we describe an implementation of a Faraday rotation measurement that has a much higher sensitivity and can be used together with proton radiography for accurate field measurements. The diagnostic makes use of the Thomson scattering probe beam and so causes little disruption to the currently available diagnostics on OMEGA. The requirement is that
![]() $n_{\text{e}}~[\text{cm}^{-3}]B~[\text{kG}]L~[\text{cm}]\geqslant 2.4\times 10^{20}~\text{kG}\cdot \text{cm}^{-2}$
, where
$n_{\text{e}}~[\text{cm}^{-3}]B~[\text{kG}]L~[\text{cm}]\geqslant 2.4\times 10^{20}~\text{kG}\cdot \text{cm}^{-2}$
, where
![]() $B$
is the magnetic field,
$B$
is the magnetic field,
![]() $n_{\text{e}}$
the electron density, and
$n_{\text{e}}$
the electron density, and
![]() $L$
the path length of the probe beam through the sample.
$L$
the path length of the probe beam through the sample.
2 Setup
The Faraday rotation measurement was implemented on a low-density turbulent plasma. The experimental setup is shown in Figure 1 (see also Ref. [Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori9]). Two
![]() $6\%$
chlorine-doped plastic foils were each irradiated with 351 nm, 5 kJ drive lasers in either a
$6\%$
chlorine-doped plastic foils were each irradiated with 351 nm, 5 kJ drive lasers in either a
![]() $5$
or 10 ns pulse. This generated two counter-propagating plasma flows, each of which then passed through a plastic grid, and collided with one another
$5$
or 10 ns pulse. This generated two counter-propagating plasma flows, each of which then passed through a plastic grid, and collided with one another
![]() ${\sim}25~\text{ns}$
after the start of the laser drive. The velocity of these flows prior to their collisions is
${\sim}25~\text{ns}$
after the start of the laser drive. The velocity of these flows prior to their collisions is
![]() ${\sim}200~\text{km}\cdot \text{s}^{-1}$
. The turbulence that resulted from this collision is expected to produce dynamically significant magnetic fields through the turbulent dynamo mechanism[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori9].
${\sim}200~\text{km}\cdot \text{s}^{-1}$
. The turbulence that resulted from this collision is expected to produce dynamically significant magnetic fields through the turbulent dynamo mechanism[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori9].

Figure 1. Experimental setup. (a) In this experiment, two
![]() $6\%$
chlorine-doped plastic foils, separated by
$6\%$
chlorine-doped plastic foils, separated by
![]() $8$
mm, were each irradiated with 351 nm, 5 kJ drive lasers in either a
$8$
mm, were each irradiated with 351 nm, 5 kJ drive lasers in either a
![]() $5$
or 10 ns pulse. This generated two counter-propagating plasma flows, each of which then passed through a plastic grid with
$5$
or 10 ns pulse. This generated two counter-propagating plasma flows, each of which then passed through a plastic grid with
![]() $300~\unicode[STIX]{x03BC}\text{m}$
hole width and hole spacing, and collided with one another at
$300~\unicode[STIX]{x03BC}\text{m}$
hole width and hole spacing, and collided with one another at
![]() ${\sim}25~\text{ns}$
after the start of the laser drive. The velocity of these flows prior to their collisions is
${\sim}25~\text{ns}$
after the start of the laser drive. The velocity of these flows prior to their collisions is
![]() ${\sim}200~\text{km}\cdot \text{s}^{-1}$
. Additional
${\sim}200~\text{km}\cdot \text{s}^{-1}$
. Additional
![]() $17$
laser beams are fired simultaneously to implode a
$17$
laser beams are fired simultaneously to implode a
![]() $420~\unicode[STIX]{x03BC}\text{m}$
diameter capsule consisting of a
$420~\unicode[STIX]{x03BC}\text{m}$
diameter capsule consisting of a
![]() $2~\unicode[STIX]{x03BC}\text{m}$
$2~\unicode[STIX]{x03BC}\text{m}$
![]() $\text{SiO}_{2}$
shell filled with
$\text{SiO}_{2}$
shell filled with
![]() $\text{D}_{2}$
gas at 6 atm and
$\text{D}_{2}$
gas at 6 atm and
![]() $^{3}$
He at 12 atm. The implosion produces mono-energetic protons at 3.3 and 15 MeV which traverse the plasma and are then collected by a CR-39 nuclear track detector[Reference Li, Séguin, Frenje, Rygg, Petrasso, Town, Amendt, Hatchett, Landen, Mackinnon, Patel, Smalyuk, Sangster and Knauer1, Reference Li, Séguin, Rygg, Frenje, Manuel, Petrasso, Betti, Delettrez, Knauer, Marshall, Meyerhofer, Shvarts, Smalyuk, Stoeckl, Landen, Town, Back and Kilkenny11, Reference Li, Séguin, Frenje, Rygg, Petrasso, Town, Amendt, Hatchett, Landen, Mackinnon, Patel, Smalyuk, Knauer, Sangster and Stoeckl12]. Thomson scattering (TS) uses a 30 J, 1 ns, frequency doubled laser beam to probe the plasma on the axis of the flow,
$^{3}$
He at 12 atm. The implosion produces mono-energetic protons at 3.3 and 15 MeV which traverse the plasma and are then collected by a CR-39 nuclear track detector[Reference Li, Séguin, Frenje, Rygg, Petrasso, Town, Amendt, Hatchett, Landen, Mackinnon, Patel, Smalyuk, Sangster and Knauer1, Reference Li, Séguin, Rygg, Frenje, Manuel, Petrasso, Betti, Delettrez, Knauer, Marshall, Meyerhofer, Shvarts, Smalyuk, Stoeckl, Landen, Town, Back and Kilkenny11, Reference Li, Séguin, Frenje, Rygg, Petrasso, Town, Amendt, Hatchett, Landen, Mackinnon, Patel, Smalyuk, Knauer, Sangster and Stoeckl12]. Thomson scattering (TS) uses a 30 J, 1 ns, frequency doubled laser beam to probe the plasma on the axis of the flow,
![]() $400~\unicode[STIX]{x03BC}\text{m}$
from the center in a
$400~\unicode[STIX]{x03BC}\text{m}$
from the center in a
![]() $50~\unicode[STIX]{x03BC}\text{m}$
focal spot toward grid B. The scattered light is collected with
$50~\unicode[STIX]{x03BC}\text{m}$
focal spot toward grid B. The scattered light is collected with
![]() $63^{\circ }$
scattering angle and the geometry is such that the scattering wavenumber is parallel to the axis of the flow. (b) Radiative hydrodynamic simulations using the code FLASH predict the electron density 36 ns after the start of the laser pulse and show the interaction region where the two jets have collided. Both proton radiography and Faraday rotation are path-integrated measurements. The proton radiography path length,
$63^{\circ }$
scattering angle and the geometry is such that the scattering wavenumber is parallel to the axis of the flow. (b) Radiative hydrodynamic simulations using the code FLASH predict the electron density 36 ns after the start of the laser pulse and show the interaction region where the two jets have collided. Both proton radiography and Faraday rotation are path-integrated measurements. The proton radiography path length,
![]() $L_{\text{PR}}$
, is equal to the scale length of the electron density, in this case 0.6 mm. The Faraday rotation path length,
$L_{\text{PR}}$
, is equal to the scale length of the electron density, in this case 0.6 mm. The Faraday rotation path length,
![]() $L_{\text{FR}}$
, is longer than that of proton radiography since the Thomson scattering region lies on the opposing side from which the probe beam originates and so passes through the interaction region (where the density is larger) twice. Consequently, in this experiment, the Faraday rotation path length
$L_{\text{FR}}$
, is longer than that of proton radiography since the Thomson scattering region lies on the opposing side from which the probe beam originates and so passes through the interaction region (where the density is larger) twice. Consequently, in this experiment, the Faraday rotation path length
![]() $L_{\text{FR}}=2L_{\text{PR}}$
. (c) Electron density along the TS beam path, from FLASH simulations[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Flocke, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, Weide, White, Reville, Miniati, Schekochihin, Froula, Gregori and Lamb13–Reference Dubey, Antypas, Ganapathy, Reid, Riley, Sheeler, Siegel and Weide16]. The electron density increases as the beam passes through the jet-interaction region.
$L_{\text{FR}}=2L_{\text{PR}}$
. (c) Electron density along the TS beam path, from FLASH simulations[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Flocke, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, Weide, White, Reville, Miniati, Schekochihin, Froula, Gregori and Lamb13–Reference Dubey, Antypas, Ganapathy, Reid, Riley, Sheeler, Siegel and Weide16]. The electron density increases as the beam passes through the jet-interaction region.
The Faraday rotation measurement is built alongside the Thomson scattering diagnostics[Reference Froula, Ross, Divol and Glenzer10], and the setup allows for a coincident measurement of the magnetic fields with proton radiography. The Thomson scattering beam is a 30 J, 1 or 3 ns pulse duration and frequency doubled (526.5 nm wavelength) laser that probes the plasma within a
![]() $50~\unicode[STIX]{x03BC}\text{m}^{3}$
region. To implement a Faraday rotation measurement, a Wollaston prism was inserted into the Thomson scattering collection optics, as shown in Figure 2. The prism splits the beam into two polarization components, labeled S and P. The two polarizations are further split such that half of each signal goes to the ion-acoustic wave (IAW) channel, which resolves ion-acoustic fluctuations, and half to the electron plasma wave (EPW) channel, which measures the total scattered power across all wavelengths. Both the IAW and EPW diagnostics are streaked in time with a 50 ps temporal resolution. Although the IAW diagnostic is spectrally resolved, since the electron features (contrary to ion-acoustic peaks in IAW) extend over a large frequency range, both polarizations cannot fit onto the EPW spectrometer and so the EPW diagnostic is not spectrally resolved.
$50~\unicode[STIX]{x03BC}\text{m}^{3}$
region. To implement a Faraday rotation measurement, a Wollaston prism was inserted into the Thomson scattering collection optics, as shown in Figure 2. The prism splits the beam into two polarization components, labeled S and P. The two polarizations are further split such that half of each signal goes to the ion-acoustic wave (IAW) channel, which resolves ion-acoustic fluctuations, and half to the electron plasma wave (EPW) channel, which measures the total scattered power across all wavelengths. Both the IAW and EPW diagnostics are streaked in time with a 50 ps temporal resolution. Although the IAW diagnostic is spectrally resolved, since the electron features (contrary to ion-acoustic peaks in IAW) extend over a large frequency range, both polarizations cannot fit onto the EPW spectrometer and so the EPW diagnostic is not spectrally resolved.

Figure 2. Faraday rotation measurement setup. A
![]() $2\unicode[STIX]{x1D714}$
, 1–3 ns pulse probe beam is scattered from a
$2\unicode[STIX]{x1D714}$
, 1–3 ns pulse probe beam is scattered from a
![]() $50~\unicode[STIX]{x03BC}\text{m}$
region of the plasma and is collected using
$50~\unicode[STIX]{x03BC}\text{m}$
region of the plasma and is collected using
![]() $f/10$
collection optics. The collected scattered light enters the insertable polarimetry setup. Four mirrors within the configuration align the scattered light onto a quartz Wollaston prism which separates the two polarizations with a
$f/10$
collection optics. The collected scattered light enters the insertable polarimetry setup. Four mirrors within the configuration align the scattered light onto a quartz Wollaston prism which separates the two polarizations with a
![]() $0.25^{\circ }$
angular separation. The scattered light is then further split and focused onto two spectrometers. The ion-acoustic wave spectrometer spectrally resolves both polarizations onto a streak camera. The electron plasma wave spectrometer measures the total scattered power across all wavelengths and so does not spectrally resolve the scattered light, and displays both polarizations onto a streak camera.
$0.25^{\circ }$
angular separation. The scattered light is then further split and focused onto two spectrometers. The ion-acoustic wave spectrometer spectrally resolves both polarizations onto a streak camera. The electron plasma wave spectrometer measures the total scattered power across all wavelengths and so does not spectrally resolve the scattered light, and displays both polarizations onto a streak camera.
Proton radiography is implemented at the OMEGA laser facility using a D
![]() $^{3}$
He capsule and CR-39 nuclear track detectors. Protons are generated by fusion reactions occurring by laser-driven implosion of a spherical capsule containing D
$^{3}$
He capsule and CR-39 nuclear track detectors. Protons are generated by fusion reactions occurring by laser-driven implosion of a spherical capsule containing D
![]() $^{3}$
He gas[Reference Petrasso, Frenje, Li, Séguin, Rygg, Schwartz, Kurebayashi, Radha, Stoeckl, Soures, Delettrez, Glebov, Meyerhofer and Sangster17]. This releases mono-energetic protons with energies of
$^{3}$
He gas[Reference Petrasso, Frenje, Li, Séguin, Rygg, Schwartz, Kurebayashi, Radha, Stoeckl, Soures, Delettrez, Glebov, Meyerhofer and Sangster17]. This releases mono-energetic protons with energies of
![]() $3.3$
and 15 MeV (accounting for Doppler shift). The protons are emitted isotropically, and thus illuminate the interaction region of the two plasma jets (see Ref. [Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori9] for additional details). The capsule is positioned far enough away from the plasma such that the protons pass through the plasma as a thin, planar sheet. Magnetic fields generated within the plasma deflect the protons, which are then imaged onto the CR-39 plates. These proton radiographs can be used to infer the magnetic field structure[Reference Bott, Graziani, Tzeferacos, White, Lamb, Gregori and Schekochihin4] within the plasma when the protons passed through. In this manner, quantities such as the mean magnetic field can be determined from the proton radiographs and then used as comparison/validation with the Faraday rotation diagnostic.
$3.3$
and 15 MeV (accounting for Doppler shift). The protons are emitted isotropically, and thus illuminate the interaction region of the two plasma jets (see Ref. [Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori9] for additional details). The capsule is positioned far enough away from the plasma such that the protons pass through the plasma as a thin, planar sheet. Magnetic fields generated within the plasma deflect the protons, which are then imaged onto the CR-39 plates. These proton radiographs can be used to infer the magnetic field structure[Reference Bott, Graziani, Tzeferacos, White, Lamb, Gregori and Schekochihin4] within the plasma when the protons passed through. In this manner, quantities such as the mean magnetic field can be determined from the proton radiographs and then used as comparison/validation with the Faraday rotation diagnostic.
3 Analysis
Both the IAW and EPW diagnostics can be analyzed in a similar manner. The difference in intensity of the two polarizations depends on three different factors. First of all, in the absence of any magnetic fields, the intensity of the S and P polarizations is determined by the relative angle between the polarization of the light and the axis of the Wollaston prism. We denote this angle by
![]() $\unicode[STIX]{x1D703}_{c}$
. In addition, the difference in intensity between the two polarizations also depends on the unequal response of the optics, detector, etc. Finally, when a magnetized plasma is present in the path, the induced rotation of the polarization angle changes the angle at which the light enters the prism and thus the ratio of the two polarizations when there is no magnetic field. The intensity of the two polarizations can be written as follows:
$\unicode[STIX]{x1D703}_{c}$
. In addition, the difference in intensity between the two polarizations also depends on the unequal response of the optics, detector, etc. Finally, when a magnetized plasma is present in the path, the induced rotation of the polarization angle changes the angle at which the light enters the prism and thus the ratio of the two polarizations when there is no magnetic field. The intensity of the two polarizations can be written as follows:
and
where
![]() $I_{\text{S}}$
and
$I_{\text{S}}$
and
![]() $I_{\text{P}}$
are the intensities of the S and P polarizations,
$I_{\text{P}}$
are the intensities of the S and P polarizations,
![]() $I_{0}$
is the initial Thomson scattering laser intensity,
$I_{0}$
is the initial Thomson scattering laser intensity,
![]() $A_{\text{S}}$
and
$A_{\text{S}}$
and
![]() $A_{\text{P}}$
are the distinct transmission factors for each polarization and
$A_{\text{P}}$
are the distinct transmission factors for each polarization and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
is the rotation due to the magnetic fields. Taking the ratio of Equations (1) and (2) gives
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
is the rotation due to the magnetic fields. Taking the ratio of Equations (1) and (2) gives
Using Equation (3), the degree of Faraday rotation (
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
) can be determined, provided that the calibration angle
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
) can be determined, provided that the calibration angle
![]() $\unicode[STIX]{x1D703}_{c}$
, the ratio of
$\unicode[STIX]{x1D703}_{c}$
, the ratio of
![]() $A_{\text{S}}$
to
$A_{\text{S}}$
to
![]() $A_{\text{P}}$
and the ratio of
$A_{\text{P}}$
and the ratio of
![]() $I_{\text{S}}$
to
$I_{\text{S}}$
to
![]() $I_{\text{P}}$
are known. To determine the ratio of
$I_{\text{P}}$
are known. To determine the ratio of
![]() $A_{\text{S}}$
to
$A_{\text{S}}$
to
![]() $A_{\text{P}}$
, a measurement with no (or weak) magnetic field was used. A half wave plate in front of the Wollaston prism is set such that incoming polarization at the prism is
$A_{\text{P}}$
, a measurement with no (or weak) magnetic field was used. A half wave plate in front of the Wollaston prism is set such that incoming polarization at the prism is
![]() $\unicode[STIX]{x1D703}_{c}=45^{\circ }$
. The axis of the Wollaston is set so that the two images from each polarization are separated along the streak camera input slit. The intensity of each polarization,
$\unicode[STIX]{x1D703}_{c}=45^{\circ }$
. The axis of the Wollaston is set so that the two images from each polarization are separated along the streak camera input slit. The intensity of each polarization,
![]() $I_{\text{S}}$
and
$I_{\text{S}}$
and
![]() $I_{\text{P}}$
, is found by integrating over the total signal for each polarization.
$I_{\text{P}}$
, is found by integrating over the total signal for each polarization.
As always, there is some stray light entering the detector. This must not be included in the Faraday rotation analysis, since it has not been scattered and so has not been influenced by the magnetic fields within the plasma. The IAW data is spectrally resolved, and since the stray light occurs at the same wavelength as the probe beam, it can be separated from the Thomson scattered signal, which instead is shifted in wavelength as the probe photons interact with the plasma. In practice, however, isolating the stray light from the scattered signal is not always possible, if for example, the frequency shifts are such that there is still a large overlap between the two. Conversely, as the EPW measurement is not spectrally resolved, there is no obvious way to disentangle the stray light from the scattering measurement. In this case, the approach is to minimize as much as possible the stray light. It is thus important to minimize stray light for both the Thomson scattering and Faraday rotation diagnostic. For Thomson scattering with IAW, the requirement is that stray light remains spectrally separated and distinguishable from the IAW peaks. Given the limited dynamic range of a streak camera, this means the stray light signal must always be of the same order (ideally smaller) than the IAW signal. These requirements become even more stringent for Faraday rotation using EPW since, as mentioned above, the signal is not spectrally resolved and so stray light directly overlaps with the scattering signal (and it is an additional source of uncertainty in the data). For EPW, we have estimated the stray light contribution by measuring the signal before and after the Thomson scattering probe laser is fired.
While the IAW and EPW data should give the same rotation angle, there are other effects that could make the two measurements differ from one another. We have already mentioned stray light. Additionally, the IAW data (being spectrally resolved) tends to be a lot noisier than the EPW data, and so the error in the measurement is larger.
4 Calibration and data shots

Figure 3. Calibration shot: (a) EPW and (b) IAW. The dots at the top and bottom of both images indicate timing fiducials and appear once every 1.1 ns and 0.548 ns, respectively. The horizontal black dashed lines in the IAW image indicate the positions of the probe laser and also the stray light. The horizontal blue dashed line in the IAW image represents the separation between the S and P polarizations and so indicates the break in the vertical wavelength axis. The lineouts underneath both images show the integrated signal of the P polarization (red) and S polarization (blue).
The calibration shot used here was a single plasma flow (where only one foil is irradiated and so there is no collision). The only magnetic fields present for this case are those from the seed fields generated from misaligned temperature and density gradients. These seed fields are small,
![]() ${\lesssim}4~\text{kG}$
[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori9], and below the detection threshold. There are of course caveats to using this calibration shot. It can be seen from the measured IAW signal, shown on the top of Figure 3(b), that the stray light from the probe laser is significant. For the IAW signal, the wavelength of the stray light is close to the lower wavelength feature. As such, only the lower wavelength peak is considered in this case. Additionally, for this particular calibration shot, while the signal is not saturated on the charge coupled device (CCD) the signal has almost certainly saturated the more sensitive streak camera later in time. Nevertheless, during the initial 1 ns, the signal remains unsaturated, has low noise and has a constant ratio between the two polarizations. Turning to the EPW data, for well over
${\lesssim}4~\text{kG}$
[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori9], and below the detection threshold. There are of course caveats to using this calibration shot. It can be seen from the measured IAW signal, shown on the top of Figure 3(b), that the stray light from the probe laser is significant. For the IAW signal, the wavelength of the stray light is close to the lower wavelength feature. As such, only the lower wavelength peak is considered in this case. Additionally, for this particular calibration shot, while the signal is not saturated on the charge coupled device (CCD) the signal has almost certainly saturated the more sensitive streak camera later in time. Nevertheless, during the initial 1 ns, the signal remains unsaturated, has low noise and has a constant ratio between the two polarizations. Turning to the EPW data, for well over
![]() $1$
ns of the shot, the signal is reliable and has an excellent signal-to-noise ratio but the contribution from stray light cannot be easily assessed, as shown in Figure 3(a).
$1$
ns of the shot, the signal is reliable and has an excellent signal-to-noise ratio but the contribution from stray light cannot be easily assessed, as shown in Figure 3(a).

Figure 4. Calibration shot: the resultant angle from both the IAW (blue) and EPW (green) data for the calibration shot. The calibration shot is a single-jet shot for which no measurable magnetic field is expected.
Figure 4 plots the initial angle
![]() $\unicode[STIX]{x1D703}_{c}$
obtained from Equation (3) (when setting
$\unicode[STIX]{x1D703}_{c}$
obtained from Equation (3) (when setting
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=0$
). By requiring that
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=0$
). By requiring that
![]() $\unicode[STIX]{x1D703}_{c}=45^{\circ }$
, this allows us to find the ratio
$\unicode[STIX]{x1D703}_{c}=45^{\circ }$
, this allows us to find the ratio
![]() $A_{\text{S}}/A_{\text{P}}$
for both the IAW and EPW channels. This gives
$A_{\text{S}}/A_{\text{P}}$
for both the IAW and EPW channels. This gives
![]() $A_{\text{S}_{\text{IAW}}}/A_{\text{P}_{\text{IAW}}}=0.33\pm 0.02$
and
$A_{\text{S}_{\text{IAW}}}/A_{\text{P}_{\text{IAW}}}=0.33\pm 0.02$
and
![]() $A_{\text{S}_{\text{EPW}}}/A_{\text{P}_{\text{EPW}}}=0.58\pm 0.02$
, where the values have been averaged over 1 ns. The difference between the calibration from IAW and EPW is likely due to the amount of stray light and intrinsic noise associated with the two channels.
$A_{\text{S}_{\text{EPW}}}/A_{\text{P}_{\text{EPW}}}=0.58\pm 0.02$
, where the values have been averaged over 1 ns. The difference between the calibration from IAW and EPW is likely due to the amount of stray light and intrinsic noise associated with the two channels.
In this section we will apply the Faraday rotation angle measurements to a few different shots in order to measure the magnetic field during and after the collision of the two plasma flows. Data from shot 1, taken 29.5 ns after the drive lasers were fired with a 10 ns pulse, is shown in Figure 5. The Thomson scattering probe has a 1 ns pulse duration and the IAW signal is close to saturation on the streak camera. The EPW data on the other hand is very good, with minimal noise, and it can be used to determine the magnetic field for this shot. In Figure 6, we report the calculated rotation angles (
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
) obtained from the IAW and EPW signals. There is a significant difference between the two curves. As mentioned, this is likely due to saturation of the IAW signal on the streak camera.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
) obtained from the IAW and EPW signals. There is a significant difference between the two curves. As mentioned, this is likely due to saturation of the IAW signal on the streak camera.

Figure 5. Shot 1: (a) EPW and (b) IAW. The dots at the top and bottom of both images indicate timing fiducials and appear once every 1.1 ns and 0.548 ns, respectively. The horizontal black dashed lines in the IAW image indicate the positions of the probe laser and also the stray light. The horizontal blue dashed line in the IAW image represents the separation between the S and P polarizations and so indicates the break in the vertical wavelength axis. The lineouts underneath both images show the integrated signal of the P polarization (red) and S polarization (blue).

Figure 6. Shot 1: resultant angle from the IAW (blue) and EPW (green) data for shot 1 averaged over 100 ps.

Figure 7. Shot 2: (a) EPW and (b) IAW. The dots at the top and bottom of both images indicate timing fiducials and appear once every 1.1 ns and 0.548 ns, respectively. The horizontal black dashed lines in the IAW image indicate the positions of the probe laser and also the stray light. The horizontal blue dashed line in the IAW image represents the separation between the S and P polarizations and so indicates the break in the vertical wavelength axis. The lineouts underneath both images show the integrated signal of the P polarization (red) and S polarization (blue).
Shot 2, taken
![]() $32.5$
ns after the drive lasers have been fired with a 5 ns pulse, also uses a 1 ns long probe beam and it is shown in Figure 7. The signal is much weaker than for shot 1. Figure 8 shows the resultant rotation angles extracted from IAW and EPW traces. We notice again that EPW gives a much better signal-to-noise ratio, and thus allows for a more precise determination of the rotation angle
$32.5$
ns after the drive lasers have been fired with a 5 ns pulse, also uses a 1 ns long probe beam and it is shown in Figure 7. The signal is much weaker than for shot 1. Figure 8 shows the resultant rotation angles extracted from IAW and EPW traces. We notice again that EPW gives a much better signal-to-noise ratio, and thus allows for a more precise determination of the rotation angle
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
.

Figure 8. Shot 2: resultant angle from the IAW (blue) and EPW (green) data for shot 2, averaged over 100 ps. The IAW data is much noisier than the EPW data because the S polarization is very weak. Despite the noisiness in the IAW data, the EPW and IAW data have a similar angular distribution.
The Faraday rotation angle is given (in SI units) by[Reference Enßlin and Vogt18]
where
![]() $L=L_{\text{PR}}$
is the path length,
$L=L_{\text{PR}}$
is the path length,
![]() $n_{\text{e}}$
is the electron density and
$n_{\text{e}}$
is the electron density and
![]() $B_{\Vert }$
is the component of the magnetic field along the path. The incident laser’s wavelength is
$B_{\Vert }$
is the component of the magnetic field along the path. The incident laser’s wavelength is
![]() $\unicode[STIX]{x1D706}=526.5~\text{nm}$
, and so implies
$\unicode[STIX]{x1D706}=526.5~\text{nm}$
, and so implies
Equation (5) indicates that once the Faraday rotation angle and electron density are known, the path-integrated field can be determined. The Faraday rotation diagnostic can resolve
![]() $1^{\circ }$
of rotation and so the requirement for the diagnostic to capture a change in magnetic field is
$1^{\circ }$
of rotation and so the requirement for the diagnostic to capture a change in magnetic field is
![]() $n_{\text{e}}~[\text{cm}^{-3}]B~[\text{kG}]L~[\text{cm}]\geqslant 2.4\times 10^{20}~\text{kG}\cdot \text{cm}^{-2}$
.
$n_{\text{e}}~[\text{cm}^{-3}]B~[\text{kG}]L~[\text{cm}]\geqslant 2.4\times 10^{20}~\text{kG}\cdot \text{cm}^{-2}$
.
In this experiment, the magnetic field is expected to be turbulent. This implies that, on average, the Faraday rotation measurement would give a null result since the mean magnetic field along the path is zero. However, while the Faraday rotation is zero on average, every single measurement must be understood in terms of a random walk through a random magnetic field, and thus the Faraday rotation value corresponds to the standard deviation of the line integral. This can be estimated by assuming a field with a correlation length,
![]() $\ell _{B}$
, equal to the grid size,
$\ell _{B}$
, equal to the grid size,
![]() $300~\unicode[STIX]{x03BC}\text{m}$
, and so the typical deviation is that acquired across one structure multiplied by the square root of the number,
$300~\unicode[STIX]{x03BC}\text{m}$
, and so the typical deviation is that acquired across one structure multiplied by the square root of the number,
![]() $N$
, of such structures encountered,
$N$
, of such structures encountered,
![]() $N=L/\ell _{B}$
. We thus obtain
$N=L/\ell _{B}$
. We thus obtain
To determine the electron density, we have employed a full photometric calibration of the IAW channel, as shown in Figure 9. This allows for the integrated number of counts on the detector to be converted into the total scattered power. To complete the full photometric calibration, a
![]() $2\unicode[STIX]{x1D714}$
fiducial laser was used. The amount of light coupled through the Thomson scattering telescope was measured using an energy meter and then cross referenced to a pick-off monitor at the start of the laser path. Laser pulses were then recorded on the Thomson scattering system and the energy measured through the cross calibrated energy meter. The transmission of the Thomson scattering probe beam through the Faraday rotation package was characterized separately as
$2\unicode[STIX]{x1D714}$
fiducial laser was used. The amount of light coupled through the Thomson scattering telescope was measured using an energy meter and then cross referenced to a pick-off monitor at the start of the laser path. Laser pulses were then recorded on the Thomson scattering system and the energy measured through the cross calibrated energy meter. The transmission of the Thomson scattering probe beam through the Faraday rotation package was characterized separately as
![]() $92.8\%$
and then included in the final calibration. The counts registered on the IAW spectrometer could then be converted to a value for the total scattered power as
$92.8\%$
and then included in the final calibration. The counts registered on the IAW spectrometer could then be converted to a value for the total scattered power as
![]() $7320\pm 930$
ADU/pJ.
$7320\pm 930$
ADU/pJ.

Figure 9. Schematic of photometric calibration setup. Scattered light from the Thomson scattering probe beam is deposited onto the IAW streak camera and recorded on a CCD as pixel counts. Initially, an energy meter is placed at the position of the IAW streak camera and records the energy of the fiducial beam once it has passed through the vacuum chamber and Thomson scattering collection optics (but not the Faraday rotation optics). The measured transmitted energy of the fiducial laser is used to calibrate a reference energy meter which records a pick-off of the fiducial laser, taken before the fiducial laser enters the vacuum chamber. The reference energy meter can then be used to determine the energy of the transmitted fiducial beam at the IAW spectrometer position. The IAW spectrometer is returned to its standard position and the transmitted energy of the fiducial laser is recorded on the IAW spectrometer as pixel counts. The reference meter then indicates the total transmitted energy to the IAW spectrometer and so a relationship between the energy transmitted to and the number of counts registered on the IAW spectrometer can be determined. Finally, the Faraday rotation setup (Wollaston prism and turning mirrors) was characterized outside of this setup, by recording the reduction in the probe beam energy due to the Faraday rotation optics, which could then be included in the final calculation.

Figure 10. Determining electron density and temperature. (a) An IAW image that can be used to determine the electron temperature of the plasma. This shot spectrally (vertical axis) and temporally (horizontal axis) resolves the ion features. A Thomson scattering spectra can then be fitted to this data to determine the electron temperature and so, through the full photometric calibration, determine the electron density for each Faraday rotation shot. The black dashed line indicates where the lineout in (b) is taken. (b) Lineout of raw data (red) from (a) with fitted spectra (blue solid line) indicating an electron temperature
![]() ${\sim}300~\text{eV}$
. It has been assumed, as predicted by FLASH simulations in Ref. [Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Flocke, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, Weide, White, Reville, Miniati, Schekochihin, Froula, Gregori and Lamb13], that the electron density is
${\sim}300~\text{eV}$
. It has been assumed, as predicted by FLASH simulations in Ref. [Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Flocke, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, Weide, White, Reville, Miniati, Schekochihin, Froula, Gregori and Lamb13], that the electron density is
![]() $10^{20}~\text{cm}^{-3}$
, the ion and electron temperatures are equal and the plasma is fully ionized, giving an average ionization
$10^{20}~\text{cm}^{-3}$
, the ion and electron temperatures are equal and the plasma is fully ionized, giving an average ionization
![]() $Z\sim 3.5$
. The sensitivity of the fitted spectra to electron density is shown by additional spectra with electron densities of
$Z\sim 3.5$
. The sensitivity of the fitted spectra to electron density is shown by additional spectra with electron densities of
![]() $5\times 10^{19}~\text{cm}^{-3}$
(purple dot-dashed line) and
$5\times 10^{19}~\text{cm}^{-3}$
(purple dot-dashed line) and
![]() $10^{19}~\text{cm}^{-3}$
(green dotted line). (c) An EPW image that can be used to determine the electron density. The vertical band at
$10^{19}~\text{cm}^{-3}$
(green dotted line). (c) An EPW image that can be used to determine the electron density. The vertical band at
![]() $526$
nm is due to a filter that eliminates the probe light. This shot spatially (vertical axis) and spectrally (horizontal axis) resolved the electron features and so fitted Thomson scattering spectra can be found to determine the electron density. Aside from the differences in the EPW diagnostic, the experimental setup for this shot is the same as those shown previously with Faraday rotation data. The white dashed line indicates where the lineout in (d) is taken. (d) Lineout of raw data (red) from (c) with fitted spectra (blue solid line) indicating an electron density
$526$
nm is due to a filter that eliminates the probe light. This shot spatially (vertical axis) and spectrally (horizontal axis) resolved the electron features and so fitted Thomson scattering spectra can be found to determine the electron density. Aside from the differences in the EPW diagnostic, the experimental setup for this shot is the same as those shown previously with Faraday rotation data. The white dashed line indicates where the lineout in (d) is taken. (d) Lineout of raw data (red) from (c) with fitted spectra (blue solid line) indicating an electron density
![]() ${\sim}5\times 10^{19}~\text{cm}^{-3}$
, similar to the value found in the full photometric calibration. The fitted spectra have an electron temperature of
${\sim}5\times 10^{19}~\text{cm}^{-3}$
, similar to the value found in the full photometric calibration. The fitted spectra have an electron temperature of
![]() $300$
eV, as determined from fitting the IAW data. The sensitivity of the fitted spectra to electron density is shown by additional spectra with electron densities of
$300$
eV, as determined from fitting the IAW data. The sensitivity of the fitted spectra to electron density is shown by additional spectra with electron densities of
![]() $4\times 10^{19}~\text{cm}^{-3}$
(green dotted line) and
$4\times 10^{19}~\text{cm}^{-3}$
(green dotted line) and
![]() $6\times 10^{19}~\text{cm}^{-3}$
(purple dot-dashed line).
$6\times 10^{19}~\text{cm}^{-3}$
(purple dot-dashed line).
The total scattered power can be used to determine the electron density via
where
![]() $P_{S}$
is the scattered power,
$P_{S}$
is the scattered power,
![]() $P_{I}$
the incident power of the probe beam,
$P_{I}$
the incident power of the probe beam,
![]() $\text{d}\unicode[STIX]{x1D6FA}$
the collecting solid angle,
$\text{d}\unicode[STIX]{x1D6FA}$
the collecting solid angle,
![]() $r_{0}=2.818\times 10^{-13}~\text{cm}$
the classical electron radius,
$r_{0}=2.818\times 10^{-13}~\text{cm}$
the classical electron radius,
![]() $\ell _{TS}=50~\unicode[STIX]{x03BC}\text{m}$
the interaction length,
$\ell _{TS}=50~\unicode[STIX]{x03BC}\text{m}$
the interaction length,
![]() $\hat{\mathbf{s}}$
the unit Poynting vector,
$\hat{\mathbf{s}}$
the unit Poynting vector,
![]() $\hat{\mathbf{E}}_{i0}$
the probe beam’s electric field unit vector,
$\hat{\mathbf{E}}_{i0}$
the probe beam’s electric field unit vector,
![]() $S(k)$
the spectral density function,
$S(k)$
the spectral density function,
![]() $Z$
the mean ion charge and
$Z$
the mean ion charge and
![]() $n_{i}$
the ion density. The incident power is provided by the on-shot calorimetry performed at the OMEGA laser facility. The effective f-number of the collection optics was
$n_{i}$
the ion density. The incident power is provided by the on-shot calorimetry performed at the OMEGA laser facility. The effective f-number of the collection optics was
![]() $9.1$
, giving a solid angle of
$9.1$
, giving a solid angle of
![]() $10^{-2}~\text{sr}$
. The spectral density function is[Reference Evans and Katzenstein19]
$10^{-2}~\text{sr}$
. The spectral density function is[Reference Evans and Katzenstein19]
which can be obtained using the spectral fit to the ion feature as shown in Figure 10. Here
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
![]() $1/k\unicode[STIX]{x1D706}_{D}$
, where
$1/k\unicode[STIX]{x1D706}_{D}$
, where
![]() $\unicode[STIX]{x1D706}_{D}$
is the Debye length. An average ionization of
$\unicode[STIX]{x1D706}_{D}$
is the Debye length. An average ionization of
![]() $Z=3.5$
is expected for CH plasmas (that is, both species are fully ionized). From this photometric calibration the electron density is found to be
$Z=3.5$
is expected for CH plasmas (that is, both species are fully ionized). From this photometric calibration the electron density is found to be
![]() ${\sim}(7\pm 1.4)\times 10^{19}~\text{cm}^{-3}$
. On a similar experimental setup where no Faraday rotation diagnostic was present and so the electron features could be spectrally resolved, the electron density could be determined by fitting the Thomson scattering spectrum to the position of the EPWs, as shown in Figure 10. In this case, the electron density was found to be
${\sim}(7\pm 1.4)\times 10^{19}~\text{cm}^{-3}$
. On a similar experimental setup where no Faraday rotation diagnostic was present and so the electron features could be spectrally resolved, the electron density could be determined by fitting the Thomson scattering spectrum to the position of the EPWs, as shown in Figure 10. In this case, the electron density was found to be
![]() $(5\pm 1)\times 10^{19}~\text{cm}^{-3}$
, similar to the value found from the photometric calibration.
$(5\pm 1)\times 10^{19}~\text{cm}^{-3}$
, similar to the value found from the photometric calibration.
Having determined the electron density and rotation angle, the path-integrated magnetic field from the Faraday rotation measurement can be calculated using Equation (5). For this experiment, the effective path length,
![]() $L_{\text{PR}}=0.06$
cm, is equal to the scale length of the electron density, as inferred from the measured self-emission X-ray images[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori9] and FLASH simulations (see Figure 1(c)). The EPW data then gives a magnetic field of 40 kG and 160 kG for shots 1 and 2, respectively (the noisier IAW data gives values of 50 kG and 190 kG for shots 1 and 2). These data shot values are well above the 4 kG seed values of the calibration shot. The strength of the Biermann battery generated seed fields for this experiment is described in Refs [Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori9, Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Flocke, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, Weide, White, Reville, Miniati, Schekochihin, Froula, Gregori and Lamb13]. Taking a field strength
$L_{\text{PR}}=0.06$
cm, is equal to the scale length of the electron density, as inferred from the measured self-emission X-ray images[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori9] and FLASH simulations (see Figure 1(c)). The EPW data then gives a magnetic field of 40 kG and 160 kG for shots 1 and 2, respectively (the noisier IAW data gives values of 50 kG and 190 kG for shots 1 and 2). These data shot values are well above the 4 kG seed values of the calibration shot. The strength of the Biermann battery generated seed fields for this experiment is described in Refs [Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori9, Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Flocke, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, Weide, White, Reville, Miniati, Schekochihin, Froula, Gregori and Lamb13]. Taking a field strength
![]() $4$
kG, path length
$4$
kG, path length
![]() $0.06$
cm and electron density
$0.06$
cm and electron density
![]() $5\times 10^{19}~\text{cm}^{-3}$
then gives a rotation angle
$5\times 10^{19}~\text{cm}^{-3}$
then gives a rotation angle
![]() $\ll 1^{\circ }$
.
$\ll 1^{\circ }$
.
5 Comparison with proton radiography
The accuracy of the Faraday rotation diagnostic can be characterized through comparison with proton radiography, a diagnostic already commissioned at the OMEGA laser facility[Reference Li, Séguin, Rygg, Frenje, Manuel, Petrasso, Betti, Delettrez, Knauer, Marshall, Meyerhofer, Shvarts, Smalyuk, Stoeckl, Landen, Town, Back and Kilkenny11, Reference Li, Séguin, Frenje, Rygg, Petrasso, Town, Amendt, Hatchett, Landen, Mackinnon, Patel, Smalyuk, Knauer, Sangster and Stoeckl12, Reference Manuel, Zylstra, Rinderknecht, Casey, Rosenberg, Sinenian, Li, Frenje, Séguin and Petrasso20]. Proton radiography was performed on the same shots as those discussed previously. Faraday rotation and proton radiography probed the plasma at essentially the same time, to within
![]() $2$
ns, which is much shorter than the hydrodynamic eddy turnover times at the largest scale, and so they both probe the same magnetic field structures. The path-integrated magnetic field reconstruction[Reference Bott, Graziani, Tzeferacos, White, Lamb, Gregori and Schekochihin4] from the proton radiographs shows the entire interaction region, as opposed to the
$2$
ns, which is much shorter than the hydrodynamic eddy turnover times at the largest scale, and so they both probe the same magnetic field structures. The path-integrated magnetic field reconstruction[Reference Bott, Graziani, Tzeferacos, White, Lamb, Gregori and Schekochihin4] from the proton radiographs shows the entire interaction region, as opposed to the
![]() $50~\unicode[STIX]{x03BC}\text{m}^{2}$
area sampled by the Faraday rotation diagnostic, as shown in Figures 11 and 12. As such, the proton radiographs can provide both a mean path-integrated field estimate for the entire region as well as the maximum path-integrated field produced at the time of the radiograph. To make a fair comparison between the two diagnostics, the mean field from the proton radiography images is calculated within a
$50~\unicode[STIX]{x03BC}\text{m}^{2}$
area sampled by the Faraday rotation diagnostic, as shown in Figures 11 and 12. As such, the proton radiographs can provide both a mean path-integrated field estimate for the entire region as well as the maximum path-integrated field produced at the time of the radiograph. To make a fair comparison between the two diagnostics, the mean field from the proton radiography images is calculated within a
![]() $200~\text{km}\cdot \text{s}^{-1}\times 2~\text{ns}\sim 0.4~\text{mm}$
square region. This region is the extent that the two
$200~\text{km}\cdot \text{s}^{-1}\times 2~\text{ns}\sim 0.4~\text{mm}$
square region. This region is the extent that the two
![]() $200~\text{km}\cdot \text{s}^{-1}$
plasma jets could travel within the
$200~\text{km}\cdot \text{s}^{-1}$
plasma jets could travel within the
![]() $2$
ns difference in diagnostic timing. Additionally, because of the geometry of the experimental setup, the Thomson scattering beam experiences about twice the path length that the protons encounter. Accordingly, to fairly compare the two diagnostics, the path-integrated magnetic field measured by the Faraday rotation diagnostic is reduced by a factor of
$2$
ns difference in diagnostic timing. Additionally, because of the geometry of the experimental setup, the Thomson scattering beam experiences about twice the path length that the protons encounter. Accordingly, to fairly compare the two diagnostics, the path-integrated magnetic field measured by the Faraday rotation diagnostic is reduced by a factor of
![]() $\sqrt{2}$
from Equation (6).
$\sqrt{2}$
from Equation (6).
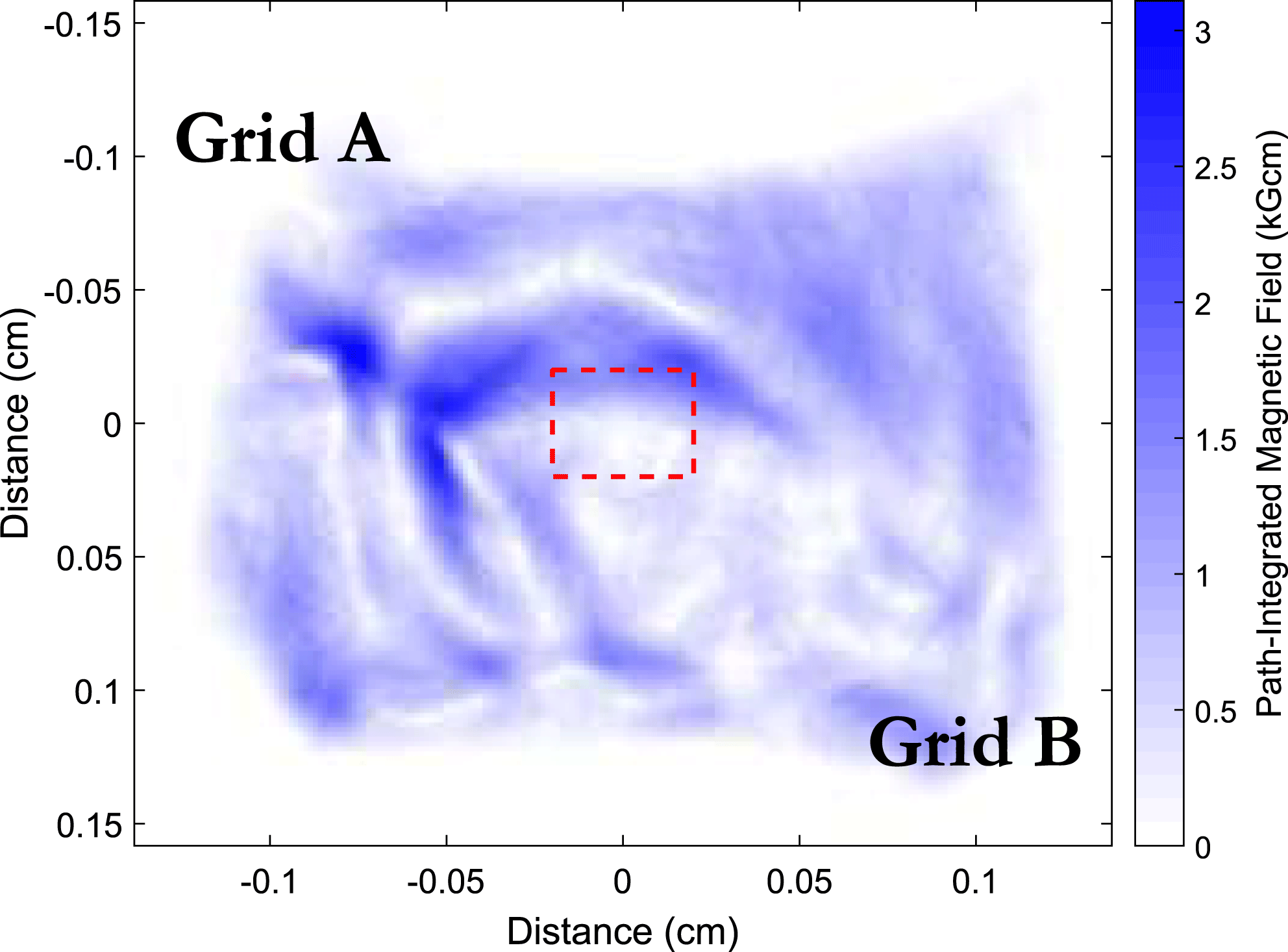
Figure 11. Shot 1: reconstructed magnetic field for shot 1. The red dashed lines indicate the extent the plasma within the Thomson scattering region can travel within the 2 ns delay between the proton radiograph and Thomson scattering measurements assuming the plasma travels at
![]() $200~\text{km}\cdot \text{s}^{-1}$
. The mean field within this red square is used for comparison with the Faraday rotation diagnostic.
$200~\text{km}\cdot \text{s}^{-1}$
. The mean field within this red square is used for comparison with the Faraday rotation diagnostic.

Figure 12. Shot 2: reconstructed magnetic field for shot 2. The red dashed lines indicate the extent the plasma within the Thomson scattering region can travel within the 2 ns delay between the proton radiograph and Thomson scattering measurements assuming the plasma travels at
![]() $200~\text{km}\cdot \text{s}^{-1}$
. The mean field within this red square is used for comparison with the Faraday rotation diagnostic.
$200~\text{km}\cdot \text{s}^{-1}$
. The mean field within this red square is used for comparison with the Faraday rotation diagnostic.

Figure 13. Comparison with proton radiography. The Faraday rotation path-integrated magnetic fields (red diamonds) for the shots described are compared with the path-integrated magnetic fields calculated from proton radiography (blue circles) for the same shots. The largest path-integrated field structure recorded by proton radiography (light-blue stars) is plotted for comparison.
Both the mean path-integrated magnetic field within the Thomson scattering region and the maximum path-integrated magnetic field as calculated from proton radiography are plotted in Figure 13. The Faraday rotation path-integrated magnetic field for each shot is estimated from the average rotation angle within the
![]() $1$
ns of signal.
$1$
ns of signal.
The error bars in the proton radiography inferred mean path-integrated field are found by sampling different 0.4 mm square regions throughout the reconstructed radiograph. There is an additional error of around
![]() $20\%$
inherent in the reconstruction algorithm which we include; this uncertainty is the result of approximations employed in the derivation of the algorithm[Reference Bott, Graziani, Tzeferacos, White, Lamb, Gregori and Schekochihin4]. The error from the Faraday rotation measurement comes from both the variability in the measured rotation angles and due to inferring the electron density from the absolute calibration. The main source of uncertainty in the Faraday rotation measurement is due to the electron density which is known to within
$20\%$
inherent in the reconstruction algorithm which we include; this uncertainty is the result of approximations employed in the derivation of the algorithm[Reference Bott, Graziani, Tzeferacos, White, Lamb, Gregori and Schekochihin4]. The error from the Faraday rotation measurement comes from both the variability in the measured rotation angles and due to inferring the electron density from the absolute calibration. The main source of uncertainty in the Faraday rotation measurement is due to the electron density which is known to within
![]() ${\sim}20\%$
. While the small difference in timing between the two diagnostics allows for changes within the path-integrated magnetic field to occur, there is a close similarity between the mean path-integrated field inferred from the two diagnostics. Additionally, the mean path-integrated field calculated from Faraday rotation is consistently smaller than the maximum path-integrated field found from the proton radiography reconstructions, as expected. The similarity in the mean magnetic field as calculated from the two diagnostics gives confidence in the results of both diagnostics, suggesting that Faraday rotation can indeed be used for on-shot analysis throughout a shot day at the OMEGA laser facility.
${\sim}20\%$
. While the small difference in timing between the two diagnostics allows for changes within the path-integrated magnetic field to occur, there is a close similarity between the mean path-integrated field inferred from the two diagnostics. Additionally, the mean path-integrated field calculated from Faraday rotation is consistently smaller than the maximum path-integrated field found from the proton radiography reconstructions, as expected. The similarity in the mean magnetic field as calculated from the two diagnostics gives confidence in the results of both diagnostics, suggesting that Faraday rotation can indeed be used for on-shot analysis throughout a shot day at the OMEGA laser facility.
6 Conclusion
We have fielded a new Faraday rotation diagnostic at the OMEGA laser facility. The analysis of the results has been described and a comparison made with the results from proton radiography. The Faraday rotation results are similar to those from proton radiography. One substantial advantage of this diagnostics is the fact that it does not rely on films or passive detectors (as CR-39). As such, analysis can be performed immediately after the shot, allowing for temporally resolved magnetic field measurements to be performed in real time during the experiment.
Acknowledgements
The research leading to these results received funding from the European Research Council under the European Community Seventh Framework Programme (FP7/2007-2013)/ ERC grant agreement No. 256973, the U.S. Department of Energy under Contract No. B591485 to Lawrence Livermore National Laboratory, Field Work Proposal No. 57789 to Argonne National Laboratory, grant Nos. DE-NA0002724 and DE-SC0016566 to the University of Chicago, and Cooperative Agreement DE-NA0001944 to the Laboratory for Laser Energetics University of Rochester. We acknowledge the support from the National Science Foundation under grant PHY-1619573. This work was also supported in part by National Institutes of Health through resources provided by the Computation Institute and the Biological Sciences Division of the University of Chicago and Argonne National Laboratory, under grant S10 RR029030-01. Awards of computer time for the simulations used to design and analyze the experiments were provided by the U.S. Department of Energy Innovative and Novel Computational Impact on Theory and Experiment (INCITE) and ASCR Leadership Computing Challenge (ALCC) programmes. This research used resources of the Argonne Leadership Computing Facility at Argonne National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under contract DE-AC02-06CH11357. Support from AWE plc., the Engineering and Physical Sciences Research Council (grant Nos. EP/M022331/1 and EP/N014472/1) and the Science and Technology Facilities Council of the United Kingdom is acknowledged.