1 Introduction
Magnetohydrodynamics (MHD) plays a fundamental role in a wide range of astrophysical phenomena, such as cooling of white dwarf stars[Reference Valyavin, Shulyak, Wade, Antonyuk, Zharikov, Galazutdinov, Plachinda, Bagnulo, Machado, Alvarez, Clark, Lopez, Hiriart, Han, Jeon, Zurita, Mujica, Burlakova, Szeifert and Burenkov1], amplification of magnetic fields (
![]() $B$
-fields) in supernova remnants[Reference Meinecke, Doyle, Miniati, Bell, Bingham, Crowston, Drake, Fatenejad, Koenig, Kuramitsu, Kuranz, Lamb, Lee, MacDonald, Murphy, Park, Pelka, Ravasio, Sakawa, Schekochihin, Scopatz, Tzeferacos, Wan, Woolsey, Yurchak, Reville and Gregori2], formation of solar flares[Reference Masuda, Kosugi, Hara, Tsuneta and Ogawara3], filamentary structures on the sun[Reference Isobe, Miyagoshi, Shibata and Yokoyama4], young stellar objects [Reference Albertazzi, Ciardi, Nakatsutsumi, Vinci, Beard, Bonito, Billette, Borghesi, Burkley, Chen, Cowan, Herrmannsdorfer, Higginson, Kroll, Pikuz, Naughton, Romagnani, Riconda, Revet, Riquier, Schlenvoigt, Skobelev, Faenov, Soloviev, Huarte-Espinosa, Frank, Portugall, Pepin and Fuchs5], accretion disks[Reference Balbus and Hawley6], and magnetic reconnection[Reference Nilson, Willingale, Kaluza, Kamperidis, Minardi, Wei, Fernandes, Notley, Bandyopadhyay, Sherlock, Kingham, Tatarakis, Najmudin, Rozmus, Evans, Haines, Dangor and Krushelnick7, Reference Zhong, Li, Wang, Wang, Dong, Xiao, Wang, Liu, Zhang, An, Wang, Zhu, Gu, He, Zhao and Zhang8]. The dynamics and stability of such astrophysical phenomena are governed by interactions between plasmas and magnetic fields, and these interactions have therefore been widely studied in laboratory experiments. Growth or suppression of hydrodynamic instabilities has been observed in plasmas in external
$B$
-fields) in supernova remnants[Reference Meinecke, Doyle, Miniati, Bell, Bingham, Crowston, Drake, Fatenejad, Koenig, Kuramitsu, Kuranz, Lamb, Lee, MacDonald, Murphy, Park, Pelka, Ravasio, Sakawa, Schekochihin, Scopatz, Tzeferacos, Wan, Woolsey, Yurchak, Reville and Gregori2], formation of solar flares[Reference Masuda, Kosugi, Hara, Tsuneta and Ogawara3], filamentary structures on the sun[Reference Isobe, Miyagoshi, Shibata and Yokoyama4], young stellar objects [Reference Albertazzi, Ciardi, Nakatsutsumi, Vinci, Beard, Bonito, Billette, Borghesi, Burkley, Chen, Cowan, Herrmannsdorfer, Higginson, Kroll, Pikuz, Naughton, Romagnani, Riconda, Revet, Riquier, Schlenvoigt, Skobelev, Faenov, Soloviev, Huarte-Espinosa, Frank, Portugall, Pepin and Fuchs5], accretion disks[Reference Balbus and Hawley6], and magnetic reconnection[Reference Nilson, Willingale, Kaluza, Kamperidis, Minardi, Wei, Fernandes, Notley, Bandyopadhyay, Sherlock, Kingham, Tatarakis, Najmudin, Rozmus, Evans, Haines, Dangor and Krushelnick7, Reference Zhong, Li, Wang, Wang, Dong, Xiao, Wang, Liu, Zhang, An, Wang, Zhu, Gu, He, Zhao and Zhang8]. The dynamics and stability of such astrophysical phenomena are governed by interactions between plasmas and magnetic fields, and these interactions have therefore been widely studied in laboratory experiments. Growth or suppression of hydrodynamic instabilities has been observed in plasmas in external
![]() $B$
-fields[Reference Sentoku, Mima, Kojima and Ruhl9–Reference Matsuo, Nagatomo, Zhang, Nicolaï, Sano, Sakata, Kojima, Lee, Law, Arikawa, Sakawa, Morita, Kuramitsu, Fujioka and Azechi12]. Moreover, in the context of high-energy-density physics (HEDP), the hydrodynamical behavior of plasmas in intense
$B$
-fields[Reference Sentoku, Mima, Kojima and Ruhl9–Reference Matsuo, Nagatomo, Zhang, Nicolaï, Sano, Sakata, Kojima, Lee, Law, Arikawa, Sakawa, Morita, Kuramitsu, Fujioka and Azechi12]. Moreover, in the context of high-energy-density physics (HEDP), the hydrodynamical behavior of plasmas in intense
![]() $B$
-fields is of great relevance to the development of
$B$
-fields is of great relevance to the development of
![]() $B$
-assisted inertial confinement fusion[Reference Chang, Fiksel, Hohenberger, Knauer, Betti, Marshall, Meyerhofer, Seguin and Petrasso13, Reference Hohenberger, Chang, Fiksel, Knauer, Betti, Marshall, Meyerhofer, Seguin and Petrasso14] and fast ignition[Reference Nagatomo, Johzaki, Sunahara, Sakagami, Mima, Shiraga and Azechi15–Reference Bailly-Grandvaux, Santos, Bellei, Forestier-Colleoni, Fujioka, Giuffrida, Honrubia, Batani, Bouillaud, Chevrot, Cross, Crowston, Dorard, Dubois, Ehret, Gregori, Hulin, Kojima, Loyez, Marquès, Morace, Nicolaï, Roth, Sakata, Schaumann, Serres, Servel, Tikhonchuk, Woolsey and Zhang20].
$B$
-assisted inertial confinement fusion[Reference Chang, Fiksel, Hohenberger, Knauer, Betti, Marshall, Meyerhofer, Seguin and Petrasso13, Reference Hohenberger, Chang, Fiksel, Knauer, Betti, Marshall, Meyerhofer, Seguin and Petrasso14] and fast ignition[Reference Nagatomo, Johzaki, Sunahara, Sakagami, Mima, Shiraga and Azechi15–Reference Bailly-Grandvaux, Santos, Bellei, Forestier-Colleoni, Fujioka, Giuffrida, Honrubia, Batani, Bouillaud, Chevrot, Cross, Crowston, Dorard, Dubois, Ehret, Gregori, Hulin, Kojima, Loyez, Marquès, Morace, Nicolaï, Roth, Sakata, Schaumann, Serres, Servel, Tikhonchuk, Woolsey and Zhang20].
In laboratory experiments, a flux density in the kilotesla region is needed to reveal the effect of
![]() $B$
-fields under the conditions of a laser-ablated high-energy-density plasma. There are several ways to generate such strong
$B$
-fields under the conditions of a laser-ablated high-energy-density plasma. There are several ways to generate such strong
![]() $B$
-fields with high-power lasers, including the important Biermann battery effect. In laser–plasma interaction, a toroidal
$B$
-fields with high-power lasers, including the important Biermann battery effect. In laser–plasma interaction, a toroidal
![]() $B$
-field is generated along the surface of the expanded plasma, where the gradients of electron density
$B$
-field is generated along the surface of the expanded plasma, where the gradients of electron density
![]() $n_{e}$
and temperature
$n_{e}$
and temperature
![]() $T_{e}$
are noncollinear[Reference Schoeffler, Loureiro, Fonseca and Silva21–Reference Li, Seguin, Frenje, Rygg, Petrasso, Town, Amendt, Hatchett, Landen, MacKinnon, Patel, Smalyuk, Sangster and Knauer23]:
$T_{e}$
are noncollinear[Reference Schoeffler, Loureiro, Fonseca and Silva21–Reference Li, Seguin, Frenje, Rygg, Petrasso, Town, Amendt, Hatchett, Landen, MacKinnon, Patel, Smalyuk, Sangster and Knauer23]:
For a higher intensity laser–plasma interaction, electrons can be accelerated to relativistic velocity. The large current density of the accelerated electrons produces a spontaneous
![]() $B$
-field surrounding the electron bunch. The strength of the
$B$
-field surrounding the electron bunch. The strength of the
![]() $B$
-field exceeds the kilotesla level inside solid[Reference Chawla, Wei, Mishra, Akli, Chen, McLean, Morace, Patel, Sawada, Sentoku, Stephens and Beg24] or gaseous targets[Reference Smyth, Sarri, Vranic, Amano, Doria, Guillaume, Habara, Heathcote, Hicks, Najmudin, Nakamura, Norreys, Kar, Silva, Tanaka, Vieira and Borghesi25, Reference Schumaker, Nakanii, McGuffey, Zulick, Chyvkov, Dollar, Habara, Kalintchenko, Maksimchuk, Tanaka, Thomas, Yanovsky and Krushelnick26].
$B$
-field exceeds the kilotesla level inside solid[Reference Chawla, Wei, Mishra, Akli, Chen, McLean, Morace, Patel, Sawada, Sentoku, Stephens and Beg24] or gaseous targets[Reference Smyth, Sarri, Vranic, Amano, Doria, Guillaume, Habara, Heathcote, Hicks, Najmudin, Nakamura, Norreys, Kar, Silva, Tanaka, Vieira and Borghesi25, Reference Schumaker, Nakanii, McGuffey, Zulick, Chyvkov, Dollar, Habara, Kalintchenko, Maksimchuk, Tanaka, Thomas, Yanovsky and Krushelnick26].
![]() $B$
-fields are not only directly produced by lasers, but may also be self-generated in plasma flow systems, as a sub-production of the perturbations[Reference Manuel, Li, Seguin, Frenje, Casey, Petrasso, Hu, Betti, Hager, Meyerhofer and Smalyuk27] or filamentations[Reference Schoeffler, Loureiro, Fonseca and Silva21, Reference Huntington, Fiuza, Ross, Zylstra, Drake, Froula, Gregori, Kugland, Kuranz, Levy, Li, Meinecke, Morita, Petrasso, Plechaty, Remington, Ryutov, Sakawa, Spitkovsky, Takabe and Park28] caused by hydrodynamic instabilities. These
$B$
-fields are not only directly produced by lasers, but may also be self-generated in plasma flow systems, as a sub-production of the perturbations[Reference Manuel, Li, Seguin, Frenje, Casey, Petrasso, Hu, Betti, Hager, Meyerhofer and Smalyuk27] or filamentations[Reference Schoeffler, Loureiro, Fonseca and Silva21, Reference Huntington, Fiuza, Ross, Zylstra, Drake, Froula, Gregori, Kugland, Kuranz, Levy, Li, Meinecke, Morita, Petrasso, Plechaty, Remington, Ryutov, Sakawa, Spitkovsky, Takabe and Park28] caused by hydrodynamic instabilities. These
![]() $B$
-fields can be further amplified to the tens of kilotesla level by plasma compression[Reference Chang, Fiksel, Hohenberger, Knauer, Betti, Marshall, Meyerhofer, Seguin and Petrasso13, Reference Hohenberger, Chang, Fiksel, Knauer, Betti, Marshall, Meyerhofer, Seguin and Petrasso14, Reference Knauer, Gotchev, Chang, Meyerhofer, Polomarov, Betti, Frenje, Li, Manuel, Petrasso, Rygg and Seguin29]. Although spontaneously generated
$B$
-fields can be further amplified to the tens of kilotesla level by plasma compression[Reference Chang, Fiksel, Hohenberger, Knauer, Betti, Marshall, Meyerhofer, Seguin and Petrasso13, Reference Hohenberger, Chang, Fiksel, Knauer, Betti, Marshall, Meyerhofer, Seguin and Petrasso14, Reference Knauer, Gotchev, Chang, Meyerhofer, Polomarov, Betti, Frenje, Li, Manuel, Petrasso, Rygg and Seguin29]. Although spontaneously generated
![]() $B$
-fields are useful in many HEDP researches, it is difficult to apply such
$B$
-fields are useful in many HEDP researches, it is difficult to apply such
![]() $B$
-fields to secondary samples, and a more easily controllable
$B$
-fields to secondary samples, and a more easily controllable
![]() $B$
-field in free space is essentially needed for many applications.
$B$
-field in free space is essentially needed for many applications.
Table 1. Laser-driven
![]() $B$
-fields.
$B$
-fields.

a
![]() $B$
-field at
$B$
-field at
![]() $650~\unicode[STIX]{x03BC}\text{m}$
from the coil center.
$650~\unicode[STIX]{x03BC}\text{m}$
from the coil center.
b This value could be overestimated, since the measured
![]() $B$
-field of 1.5 kT might not result directly from the coil, and plasma compression effects could also be included.
$B$
-field of 1.5 kT might not result directly from the coil, and plasma compression effects could also be included.
c
![]() $B$
-field at
$B$
-field at
![]() $250~\unicode[STIX]{x03BC}\text{m}$
from the coil center.
$250~\unicode[STIX]{x03BC}\text{m}$
from the coil center.
d
![]() $I\unicode[STIX]{x1D706}^{2}$
of laser irradiated on each CC target.
$I\unicode[STIX]{x1D706}^{2}$
of laser irradiated on each CC target.
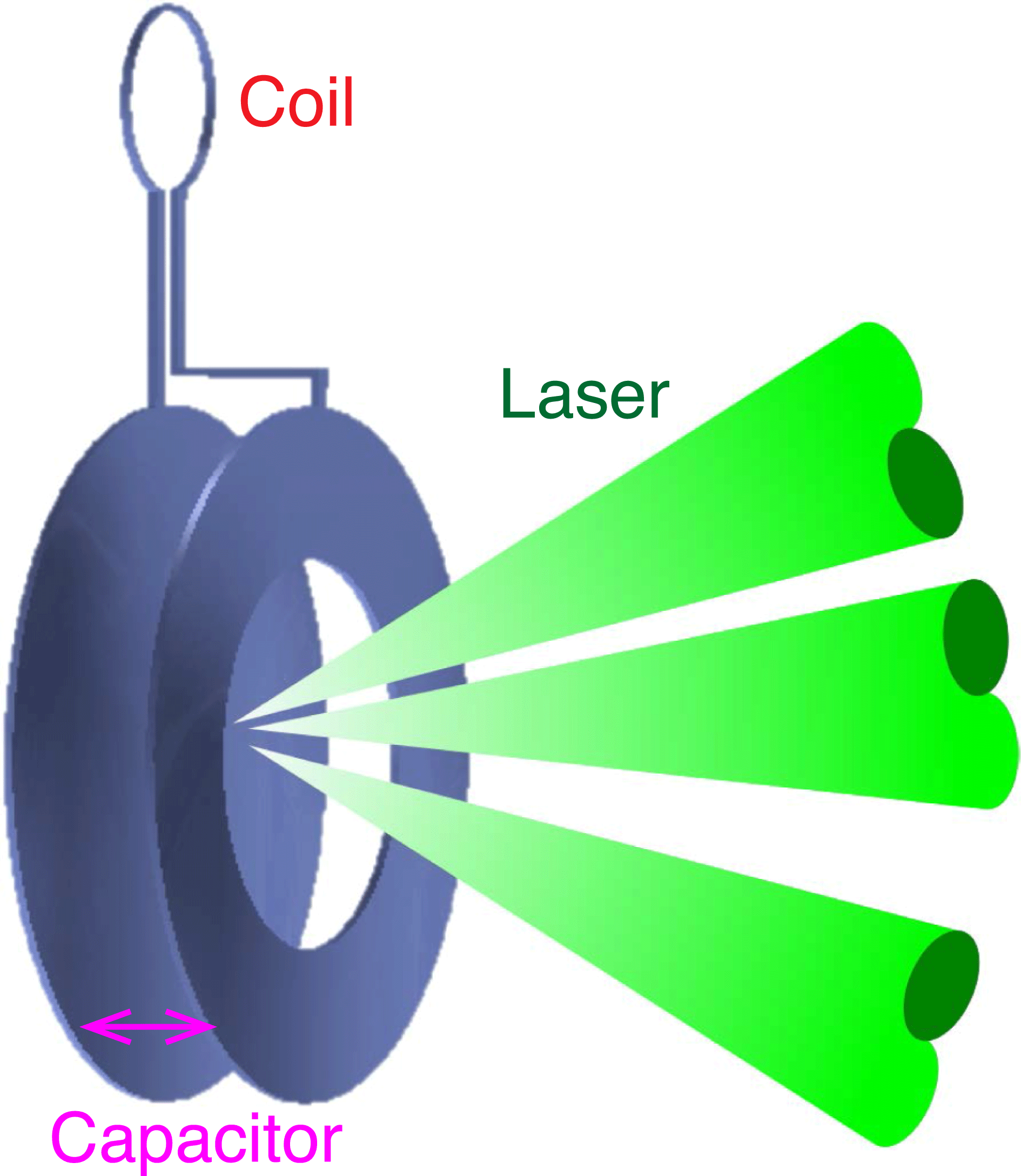
Figure 1. Basic geometry of the capacitor–coil target.
The use of a capacitor–coil (CC) target to generate a controllable
![]() $B$
-field was proposed and realized on the Lekko VIII laser system by Daido et al.
[Reference Daido, Miki, Mima, Fujita, Sawai and Fujita30] in 1986. Courtois et al.
[Reference Courtois, Ash, Chambers, Grundy and Woolsey31] used a similar mechanism with a Helmholtz coil on the Vulcan laser at the Central Laser Facility in the United Kingdom and obtained a
$B$
-field was proposed and realized on the Lekko VIII laser system by Daido et al.
[Reference Daido, Miki, Mima, Fujita, Sawai and Fujita30] in 1986. Courtois et al.
[Reference Courtois, Ash, Chambers, Grundy and Woolsey31] used a similar mechanism with a Helmholtz coil on the Vulcan laser at the Central Laser Facility in the United Kingdom and obtained a
![]() $B$
-field of a few tesla. In 2013, Fujioka et al.
[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi32] redesigned the CC target and used it on the Gekko XII high-power laser facility. A kilotesla level
$B$
-field of a few tesla. In 2013, Fujioka et al.
[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi32] redesigned the CC target and used it on the Gekko XII high-power laser facility. A kilotesla level
![]() $B$
-field was achieved with a laser energy of 1.5 kJ in 1 ns[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi32]. As shown in Figure 1, the target is composed of two main parts: a capacitor and a connection coil. The capacitor is formed from two metallic disks placed parallel to each other. There is a hole in the front disk that allows the laser to propagate through and focus on the rear disk. The two disks are connected by the connection coil, which generates a
$B$
-field was achieved with a laser energy of 1.5 kJ in 1 ns[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi32]. As shown in Figure 1, the target is composed of two main parts: a capacitor and a connection coil. The capacitor is formed from two metallic disks placed parallel to each other. There is a hole in the front disk that allows the laser to propagate through and focus on the rear disk. The two disks are connected by the connection coil, which generates a
![]() $B$
-field when the discharge current flows through it.
$B$
-field when the discharge current flows through it.
In the past few years, laser-driven coils have been applied in many laboratories with similar targets. Some typical results with nanosecond high-power lasers are listed in Table 1, together with the results from Daido et al. and Courtois et al. for comparison. The targets used are illustrated in Figure 2. Pei et al.
[Reference Pei, Zhong, Sakawa, Zhang, Zhang, Wei, Li, Li, Zhu, Sano, Hara, Kondo, Fujioka, Liang, Wang and Zhao33] used a double-U-turn Helmholtz coil instead of a single coil to produce a counter
![]() $B$
-field between the coils for magnetic reconnection research. Santos et al.
[Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, D’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyè, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey35] modified the angle of the coil and the size of the disks to match the setting of the LULI laser facility. A U-shaped foil target was used on Omega by Goyon et al.
[Reference Goyon, Pollock, Turnbull, Hazi, Divol, Farmer, Haberberger, Javedani, Johnson, Kemp, Levy, Grant Logan, Mariscal, Landen, Patankar, Ross, Rubenchik, Swadling, Williams, Fujioka, Law and Moody37]. In contrast to the targets described above, Zhu et al.
[Reference Zhu, Li, Yuan, Li, Li, Liao, Zhao, Zhong, Xue, He, Wang, Lu, Zhang, Yang, Zhou, Xie, Hong, Wei, Zhang, Han, Pei, Liu, Zhang, Zhu, Gu, Zhao, Zhang, Zhao and Zhang38] used a simpler design with only one single open-ended coil.
$B$
-field between the coils for magnetic reconnection research. Santos et al.
[Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, D’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyè, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey35] modified the angle of the coil and the size of the disks to match the setting of the LULI laser facility. A U-shaped foil target was used on Omega by Goyon et al.
[Reference Goyon, Pollock, Turnbull, Hazi, Divol, Farmer, Haberberger, Javedani, Johnson, Kemp, Levy, Grant Logan, Mariscal, Landen, Patankar, Ross, Rubenchik, Swadling, Williams, Fujioka, Law and Moody37]. In contrast to the targets described above, Zhu et al.
[Reference Zhu, Li, Yuan, Li, Li, Liao, Zhao, Zhong, Xue, He, Wang, Lu, Zhang, Yang, Zhou, Xie, Hong, Wei, Zhang, Han, Pei, Liu, Zhang, Zhu, Gu, Zhao, Zhang, Zhao and Zhang38] used a simpler design with only one single open-ended coil.
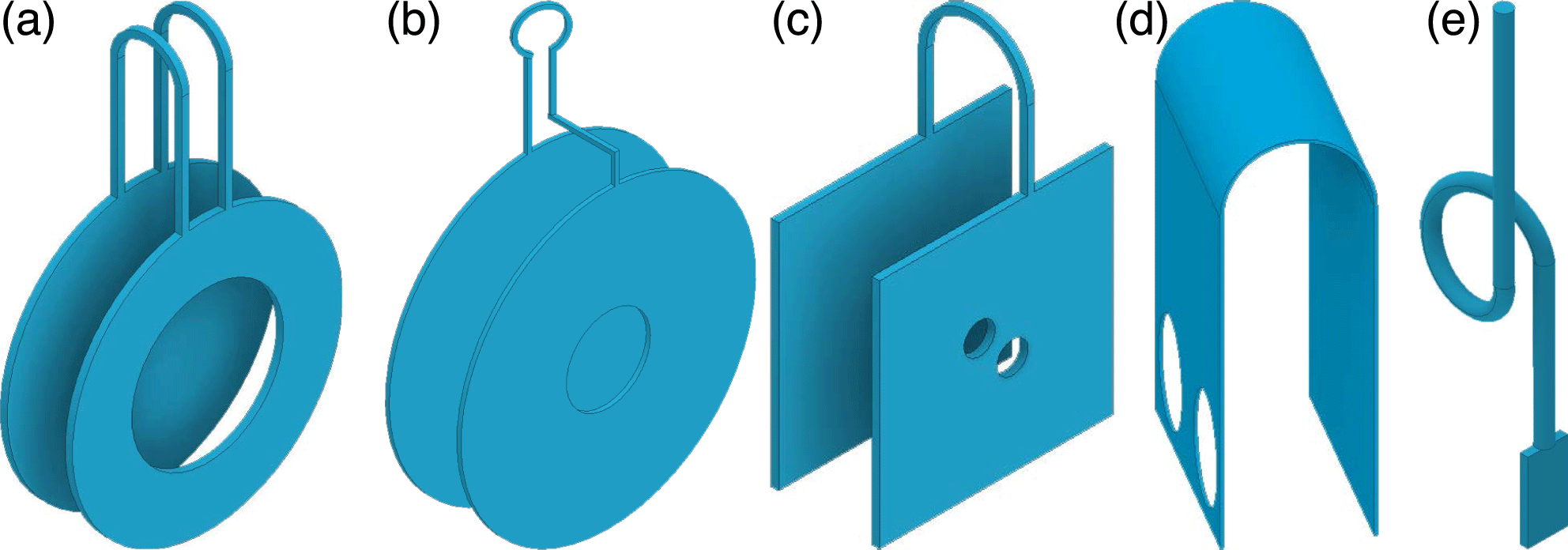
Figure 2. The illustration of targets used in (a) Ref. [Reference Pei, Zhong, Sakawa, Zhang, Zhang, Wei, Li, Li, Zhu, Sano, Hara, Kondo, Fujioka, Liang, Wang and Zhao33], (b) Ref. [Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, D’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyè, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey35], (c) Ref. [Reference Gao, Ji, Fiksel, Fox, Evans and Alfonso36], (d) Ref. [Reference Goyon, Pollock, Turnbull, Hazi, Divol, Farmer, Haberberger, Javedani, Johnson, Kemp, Levy, Grant Logan, Mariscal, Landen, Patankar, Ross, Rubenchik, Swadling, Williams, Fujioka, Law and Moody37], and (e) Ref. [Reference Zhu, Li, Yuan, Li, Li, Liao, Zhao, Zhong, Xue, He, Wang, Lu, Zhang, Yang, Zhou, Xie, Hong, Wei, Zhang, Han, Pei, Liu, Zhang, Zhu, Gu, Zhao, Zhang, Zhao and Zhang38].
2 Generation of the
 $B$
-field
$B$
-field
The main mechanism of laser-driven
![]() $B$
-field generation involves two steps: establishment of an electrical potential and, as a consequence, generation of a
$B$
-field generation involves two steps: establishment of an electrical potential and, as a consequence, generation of a
![]() $B$
-field by the driven current.
$B$
-field by the driven current.
2.1 Establishment of a potential with the laser
First, when a laser pulse irradiates a disk, some electrons are heated. Suprathermal electrons escape from the disk surface, and a potential barrier is created[Reference Poyé, Dubois, Lubrano-Lavaderci, D’Humiéres, Bardon, Hulin, Bailly-Grandvaux, Ribolzi, Raffestin, Santos, Nicolaï and Tikhonchuk39, Reference Dubois, Lubrano-Lavaderci, Raffestin, Ribolzi, Gazave, Fontaine, D’Humières, Hulin, Nicola, Poyè and Tikhonchuk40]. This barrier potential pulls back a fraction of the escaping electrons and, at the same time, induces a return current inside the target to neutralize the charge. In comparison with a single open-ended coil[Reference Zhu, Li, Yuan, Li, Li, Liao, Zhao, Zhong, Xue, He, Wang, Lu, Zhang, Yang, Zhou, Xie, Hong, Wei, Zhang, Han, Pei, Liu, Zhang, Zhu, Gu, Zhao, Zhang, Zhao and Zhang38], the front disk on the CC target captures a proportion of the escaping electrons, thereby enhancing the potential.
The initial potential is dominated by the effect of the irradiating laser, although it is also affected by the disk material. To increase the initial potential, it is necessary to increase the number of escaping electrons. The number of escaping electrons, and thus their total charge, is determined by both the suprathermal electron temperature
![]() $T_{e}$
and the barrier potential
$T_{e}$
and the barrier potential
![]() $V_{b}$
. Considering a simple model and assuming a static barrier potential of
$V_{b}$
. Considering a simple model and assuming a static barrier potential of
![]() $V_{b}$
, only electrons with an energy greater than
$V_{b}$
, only electrons with an energy greater than
![]() $qV_{b}$
can escape from the target surface. Assuming an energy distribution for the suprathermal electrons with an exponential high-energy tail of the form
$qV_{b}$
can escape from the target surface. Assuming an energy distribution for the suprathermal electrons with an exponential high-energy tail of the form
the total number of electrons
![]() $N_{\text{tot}}$
and the number of electrons that escape
$N_{\text{tot}}$
and the number of electrons that escape
![]() $N_{\text{esc}}$
can be estimated as
$N_{\text{esc}}$
can be estimated as
respectively, where
![]() $E_{\text{laser}}$
is the laser energy and
$E_{\text{laser}}$
is the laser energy and
![]() $\unicode[STIX]{x1D702}$
is the absorption fraction. For unit laser energy at constant absorption, the number of escaping electrons per unit laser energy is plotted in Figure 3 as a function of
$\unicode[STIX]{x1D702}$
is the absorption fraction. For unit laser energy at constant absorption, the number of escaping electrons per unit laser energy is plotted in Figure 3 as a function of
![]() $T_{e}$
normalized by the barrier potential
$T_{e}$
normalized by the barrier potential
![]() $V_{b}$
. The number of escaping electrons reaches a maximum value when
$V_{b}$
. The number of escaping electrons reaches a maximum value when
![]() $T_{e}$
is equal to
$T_{e}$
is equal to
![]() $V_{b}$
. The existence of an optimal
$V_{b}$
. The existence of an optimal
![]() $T_{e}$
can be understood as the result of competition between the suprathermal electrons and the escaping fraction. With a higher
$T_{e}$
can be understood as the result of competition between the suprathermal electrons and the escaping fraction. With a higher
![]() $T_{e}$
, more electrons exceed the barrier potential and escape from the target surface, and, with a fixed absorption of laser energy, the total number of suprathermal electrons is decreased. Since
$T_{e}$
, more electrons exceed the barrier potential and escape from the target surface, and, with a fixed absorption of laser energy, the total number of suprathermal electrons is decreased. Since
![]() $T_{e}$
is related to the laser irradiance
$T_{e}$
is related to the laser irradiance
![]() $I\unicode[STIX]{x1D706}^{2}$
, it is possible, for a known absorption mechanism, to find the optimal incident laser parameters to maximize the potential. However, the laser absorption
$I\unicode[STIX]{x1D706}^{2}$
, it is possible, for a known absorption mechanism, to find the optimal incident laser parameters to maximize the potential. However, the laser absorption
![]() $\unicode[STIX]{x1D702}$
depends on the laser irradiance, and
$\unicode[STIX]{x1D702}$
depends on the laser irradiance, and
![]() $V_{b}$
is strongly dependent on electron heating and escape, so more sophisticated models are needed to provide more realistic solutions. However, this discussion is beyond the scope of this article.
$V_{b}$
is strongly dependent on electron heating and escape, so more sophisticated models are needed to provide more realistic solutions. However, this discussion is beyond the scope of this article.
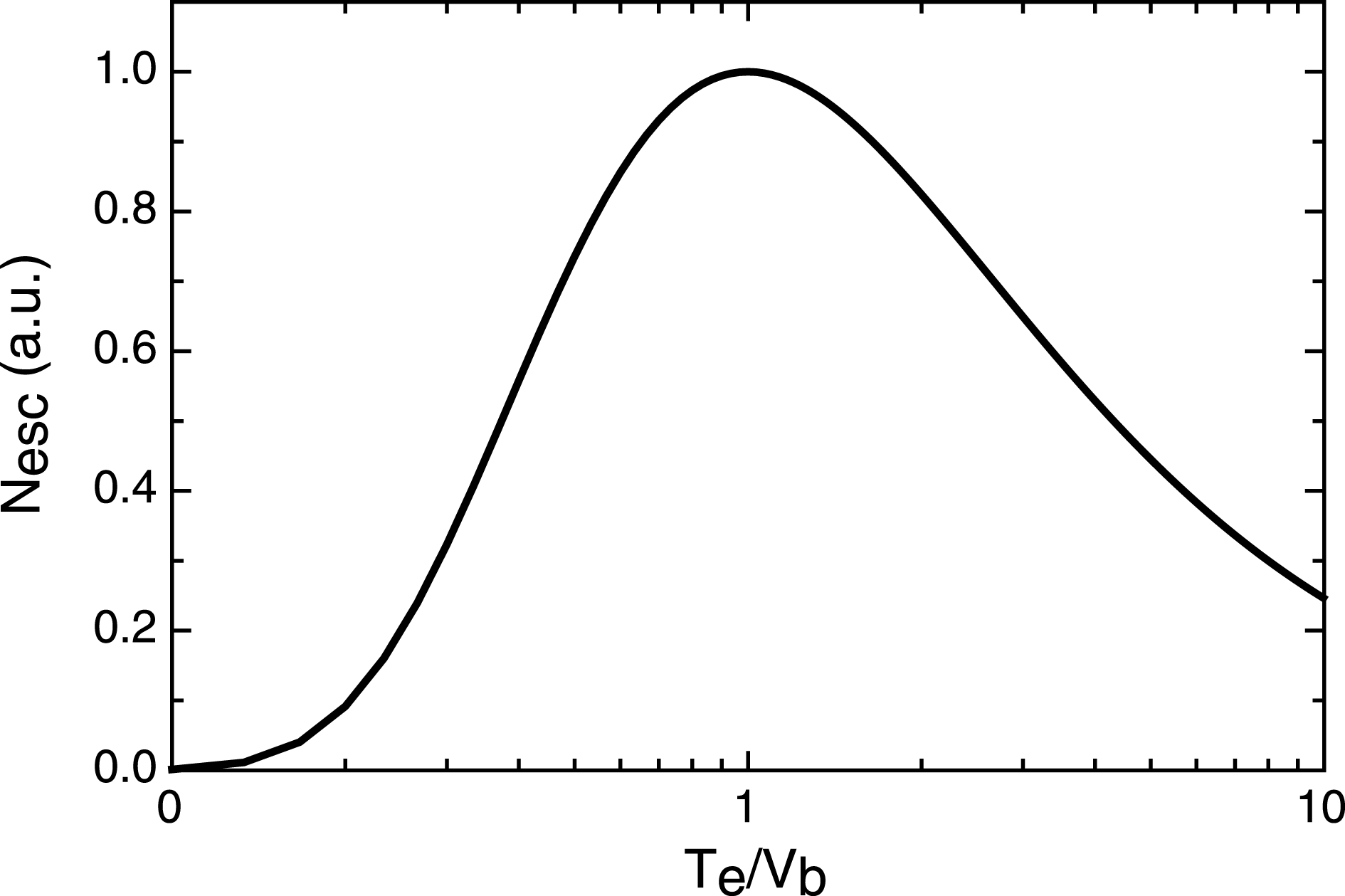
Figure 3. The number of escaping electrons per unit laser energy as a function of
![]() $T_{e}/V_{b}$
.
$T_{e}/V_{b}$
.
2.2 Generation of the
 $B$
-field
$B$
-field
With the establishment of an initial potential
![]() $V_{0}$
between the two disks, the target behaves toward the potential like a resistor–inductor (
$V_{0}$
between the two disks, the target behaves toward the potential like a resistor–inductor (
![]() $RL$
) electrical circuit. The time evolution of the current
$RL$
) electrical circuit. The time evolution of the current
![]() $I(t)$
can be treated using an
$I(t)$
can be treated using an
![]() $RL$
model:
$RL$
model:
where
![]() $L$
and
$L$
and
![]() $R$
are the inductance and resistance, respectively. For the targets illustrated in Figure 2, the resistance is usually negligibly small compared with the inductance. Reducing the inductance by reshaping the coil could result in a higher peak current. However, we should also note that the coil shape also determines the spatio-temporal ranges of the
$R$
are the inductance and resistance, respectively. For the targets illustrated in Figure 2, the resistance is usually negligibly small compared with the inductance. Reducing the inductance by reshaping the coil could result in a higher peak current. However, we should also note that the coil shape also determines the spatio-temporal ranges of the
![]() $B$
-field. An appropriate balance should be found between the peak strength and distribution of the
$B$
-field. An appropriate balance should be found between the peak strength and distribution of the
![]() $B$
-field, depending on the intended application.
$B$
-field, depending on the intended application.
2.3 Discussion
The
![]() $B$
-field, generated by the potential
$B$
-field, generated by the potential
![]() $V_{0}$
and the current in the coil
$V_{0}$
and the current in the coil
![]() $I(t)$
, is controlled by both the incident laser and the shape of the target. For example, from a comparison of the results of Daido et al.
[Reference Daido, Miki, Mima, Fujita, Sawai and Fujita30] and Fujioka et al.
[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi32], it can be seen that although similar target geometries were applied, the strength of the
$I(t)$
, is controlled by both the incident laser and the shape of the target. For example, from a comparison of the results of Daido et al.
[Reference Daido, Miki, Mima, Fujita, Sawai and Fujita30] and Fujioka et al.
[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi32], it can be seen that although similar target geometries were applied, the strength of the
![]() $B$
-field was increased over 25 times by increasing the laser energy by a factor of 15. Furthermore, although the use of a Helmholtz coil by Courtois et al.
[Reference Courtois, Ash, Chambers, Grundy and Woolsey31] dramatically increased the inductance and thus decreased the peak
$B$
-field was increased over 25 times by increasing the laser energy by a factor of 15. Furthermore, although the use of a Helmholtz coil by Courtois et al.
[Reference Courtois, Ash, Chambers, Grundy and Woolsey31] dramatically increased the inductance and thus decreased the peak
![]() $B$
-field, the duration of the field was increased compared with the case of a single coil, and much better spatial uniformity was achieved. Thus, it is necessary to consider not only the peak strength of the
$B$
-field, the duration of the field was increased compared with the case of a single coil, and much better spatial uniformity was achieved. Thus, it is necessary to consider not only the peak strength of the
![]() $B$
-field, but also its temporal evolution and spatial distribution.
$B$
-field, but also its temporal evolution and spatial distribution.
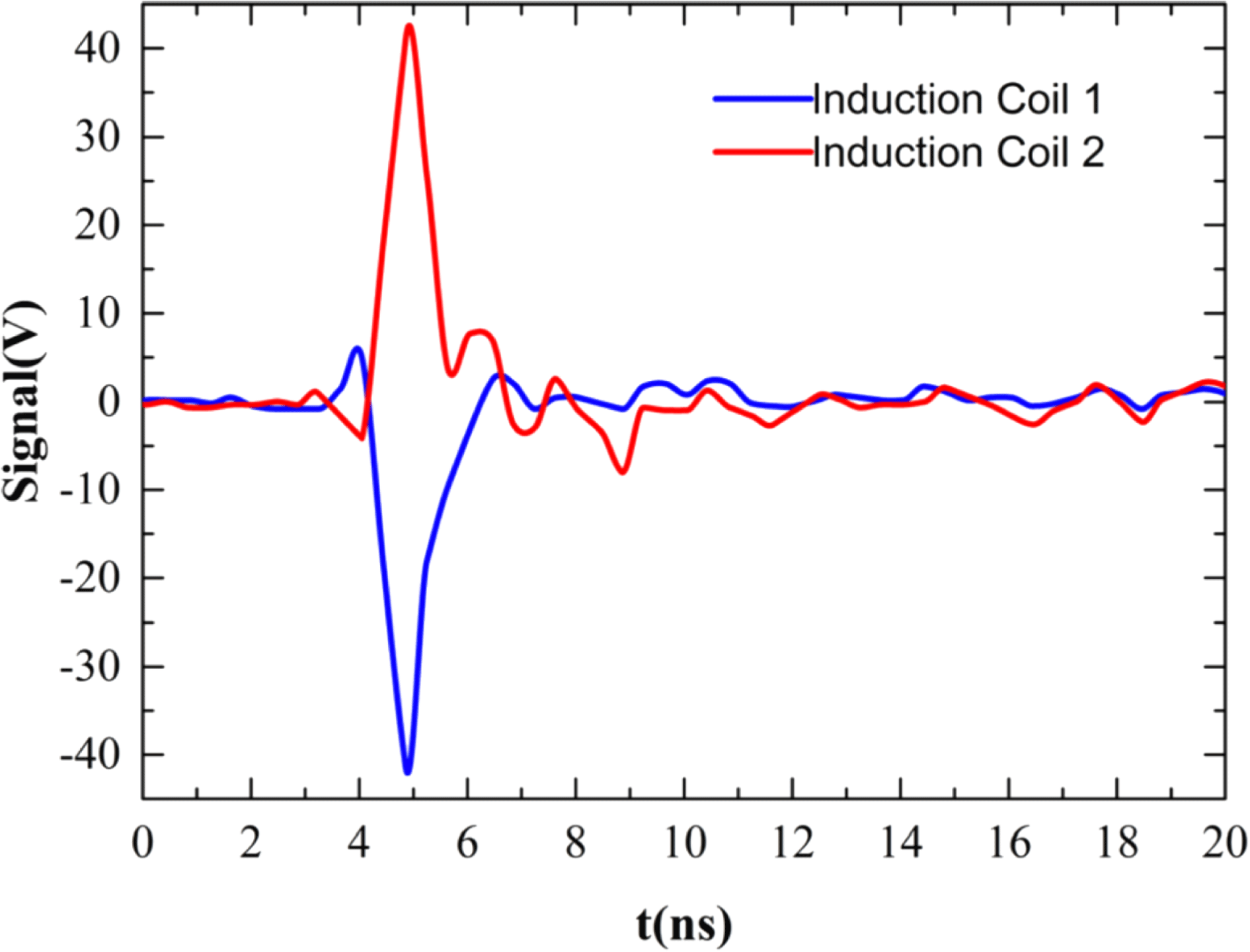
Figure 4. Typical symmetric signal observed with a differential twisted pair[Reference Zhu, Li, Yuan, Li, Li, Liao, Zhao, Zhong, Xue, He, Wang, Lu, Zhang, Yang, Zhou, Xie, Hong, Wei, Zhang, Han, Pei, Liu, Zhang, Zhu, Gu, Zhao, Zhang, Zhao and Zhang38].
As well as those mentioned in the above discussion, some other models have been proposed for the study of laser-driven
![]() $B$
-fields[Reference Fiksel, Fox, Gao and Ji41–Reference Schillaci, De Marco, Giuffrida, Fujioka, Zhang, Korn and Margarone43].
$B$
-fields[Reference Fiksel, Fox, Gao and Ji41–Reference Schillaci, De Marco, Giuffrida, Fujioka, Zhang, Korn and Margarone43].
3 Measurement of the
 $B$
-field
$B$
-field
3.1 B-dot probe
A rapidly changing
![]() $B$
-field can be measured in many ways. One traditional method uses a pick-up coil, also known as a B-dot probe. The basic idea is to utilize Faraday’s law to measure
$B$
-field can be measured in many ways. One traditional method uses a pick-up coil, also known as a B-dot probe. The basic idea is to utilize Faraday’s law to measure
![]() $B$
-field fluctuations
$B$
-field fluctuations
![]() $\text{d}B/\text{d}t$
[Reference Phillips and Turner44]. However, B-dot measurements usually suffer from strong electromagnetic pulse noise from laser–plasma interactions, and it is therefore necessary to adopt techniques that can distinguish between the signal from the magnetic coil and that from laser–plasma interactions. First of all, for a single B-dot probe, the probe should consist of a differentially twisted pair so that symmetric signals then indicate a
$\text{d}B/\text{d}t$
[Reference Phillips and Turner44]. However, B-dot measurements usually suffer from strong electromagnetic pulse noise from laser–plasma interactions, and it is therefore necessary to adopt techniques that can distinguish between the signal from the magnetic coil and that from laser–plasma interactions. First of all, for a single B-dot probe, the probe should consist of a differentially twisted pair so that symmetric signals then indicate a
![]() $B$
-field, while asymmetric signals might be caused by heating of the probe by high-energy particles or X-rays. Figure 4 shows a typical signal obtained by Zhu et al.
[Reference Zhu, Li, Yuan, Li, Li, Liao, Zhao, Zhong, Xue, He, Wang, Lu, Zhang, Yang, Zhou, Xie, Hong, Wei, Zhang, Han, Pei, Liu, Zhang, Zhu, Gu, Zhao, Zhang, Zhao and Zhang38], in which two symmetric pulses from the differential pair can be clearly seen. Other approaches to alleviating the noise problem involve placing multiple B-dot probes at different positions or using a multidimensional B-dot probe that detects the
$B$
-field, while asymmetric signals might be caused by heating of the probe by high-energy particles or X-rays. Figure 4 shows a typical signal obtained by Zhu et al.
[Reference Zhu, Li, Yuan, Li, Li, Liao, Zhao, Zhong, Xue, He, Wang, Lu, Zhang, Yang, Zhou, Xie, Hong, Wei, Zhang, Han, Pei, Liu, Zhang, Zhu, Gu, Zhao, Zhang, Zhao and Zhang38], in which two symmetric pulses from the differential pair can be clearly seen. Other approaches to alleviating the noise problem involve placing multiple B-dot probes at different positions or using a multidimensional B-dot probe that detects the
![]() $B$
-field along three orthogonal axes at the same point[Reference Everson, Pribyl, Constantin, Zylstra, Schaeffer, Kugland and Niemann45]. Since the
$B$
-field along three orthogonal axes at the same point[Reference Everson, Pribyl, Constantin, Zylstra, Schaeffer, Kugland and Niemann45]. Since the
![]() $B$
-field generated from a laser-driven coil is strongly directional, while the noise from laser–plasma interactions is relatively isotropic, the
$B$
-field generated from a laser-driven coil is strongly directional, while the noise from laser–plasma interactions is relatively isotropic, the
![]() $B$
-field from the coil can be extracted by comparing signals at different points or from different directions. One disadvantage of the B-dot probe concerns bandwidth. For a
$B$
-field from the coil can be extracted by comparing signals at different points or from different directions. One disadvantage of the B-dot probe concerns bandwidth. For a
![]() $B$
-field driven by a picosecond or femtosecond laser, the rise time can be at a picosecond scale, so the bandwidth of the B-dot probe and that of the oscilloscope need to be very high to evaluate the peak of the
$B$
-field driven by a picosecond or femtosecond laser, the rise time can be at a picosecond scale, so the bandwidth of the B-dot probe and that of the oscilloscope need to be very high to evaluate the peak of the
![]() $B$
-field, and this is very hard to achieve.
$B$
-field, and this is very hard to achieve.
3.2 Optical probe
Another approach to measuring the
![]() $B$
-field involves the use of an optical diagnostic technique, such as that based on the Faraday effect. The Faraday effect is a magneto-optical phenomenon in which, when polarized light propagates through a magneto-optical medium in a
$B$
-field involves the use of an optical diagnostic technique, such as that based on the Faraday effect. The Faraday effect is a magneto-optical phenomenon in which, when polarized light propagates through a magneto-optical medium in a
![]() $B$
-field, the plane of polarization is rotated, with the angle of rotation being proportional to the strength of the
$B$
-field, the plane of polarization is rotated, with the angle of rotation being proportional to the strength of the
![]() $B$
-field in the direction of propagation:
$B$
-field in the direction of propagation:
where
![]() $L$
is the length of the optical path,
$L$
is the length of the optical path,
![]() $V$
is the Verdet constant, and
$V$
is the Verdet constant, and
![]() $B_{L}$
is the component of the
$B_{L}$
is the component of the
![]() $B$
-field parallel to the direction of propagation of the probe laser beam. Such a method was applied using a SiO
$B$
-field parallel to the direction of propagation of the probe laser beam. Such a method was applied using a SiO
![]() $_{2}$
crystal by Fujioka et al.
[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi32] and later using a terbium gallium garnet by Santos et al.
[Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, D’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyè, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey35]. Both experiments used a streak camera as the detector to obtain measurements with high temporal resolution. A typical setup for a Faraday effect measurement is shown in Figure 5(a). A Faraday crystal is positioned beside the magnetic coil, with a linearly polarized probe laser beam propagating through it. On applying the
$_{2}$
crystal by Fujioka et al.
[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi32] and later using a terbium gallium garnet by Santos et al.
[Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, D’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyè, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey35]. Both experiments used a streak camera as the detector to obtain measurements with high temporal resolution. A typical setup for a Faraday effect measurement is shown in Figure 5(a). A Faraday crystal is positioned beside the magnetic coil, with a linearly polarized probe laser beam propagating through it. On applying the
![]() $B$
-field generated by the coil to the crystal, the plane of polarization is rotated. By means of a Wollaston prism, the probe beam is divided into two orthogonal linearly polarized components. Both outgoing beams are imaged on the slit of a streak camera to measure the temporal evolution. An example from Ref. [Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi32] is shown in Figures 5(b) and 5(c). A reference image was taken without a
$B$
-field generated by the coil to the crystal, the plane of polarization is rotated. By means of a Wollaston prism, the probe beam is divided into two orthogonal linearly polarized components. Both outgoing beams are imaged on the slit of a streak camera to measure the temporal evolution. An example from Ref. [Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi32] is shown in Figures 5(b) and 5(c). A reference image was taken without a
![]() $B$
-field driven laser. The probe beam was horizontally polarized and appeared only on the right side of the image. With a laser-driven
$B$
-field driven laser. The probe beam was horizontally polarized and appeared only on the right side of the image. With a laser-driven
![]() $B$
-field, the plane of polarization was rotated, with the vertically polarized component appearing on the left side. The angle of rotation
$B$
-field, the plane of polarization was rotated, with the vertically polarized component appearing on the left side. The angle of rotation
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
can then be estimated from the change in the intensity ratio for both polarization components as follows:
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
can then be estimated from the change in the intensity ratio for both polarization components as follows:
where
![]() $I_{\text{left}}$
and
$I_{\text{left}}$
and
![]() $I_{\text{right}}$
are the intensities of the probe beam read from the streak camera. The strength of the
$I_{\text{right}}$
are the intensities of the probe beam read from the streak camera. The strength of the
![]() $B$
-field can be then estimated from the value of
$B$
-field can be then estimated from the value of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
, using Equation (6).
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
, using Equation (6).
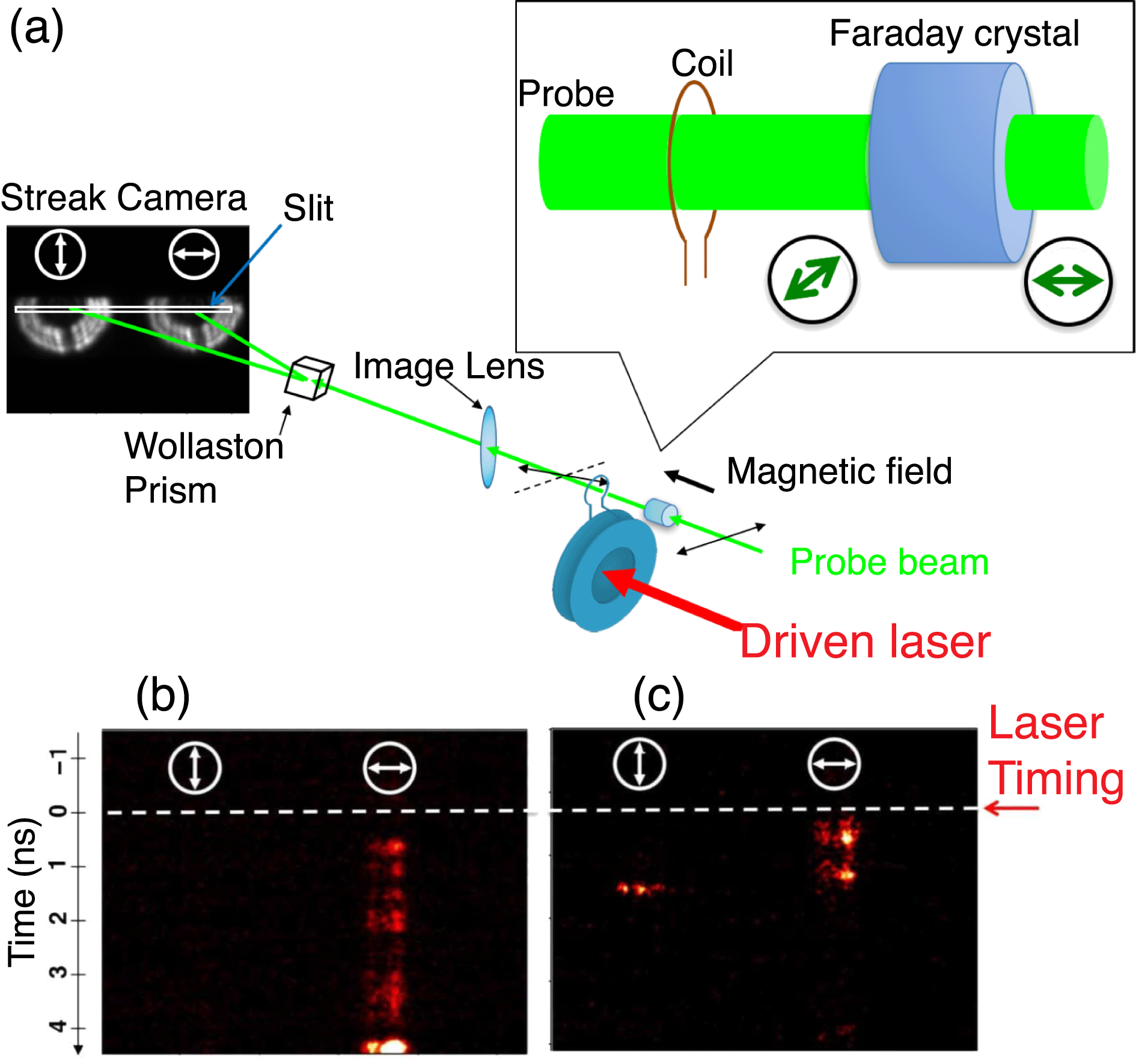
Figure 5. Example of a Faraday rotation measurement: (a) typical setup; (b) reference image; (c) image in the presence of a
![]() $B$
-field[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi32].
$B$
-field[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi32].
Another approach applies the Cotton–Mouton effect, which occurs when a Cotton–Mouton medium is subjected to a
![]() $B$
-field[Reference Sandhu, Dharmadhikari, Rajeev, Kumar, Sengupta, Das and Kaw46, Reference Shaikh, Lad, Jana, Sarkar, Dey and Kumar47]. A linearly polarized probe laser beam becomes elliptically polarized owing to the Cotton–Mouton effect, and, by measuring the ellipticity
$B$
-field[Reference Sandhu, Dharmadhikari, Rajeev, Kumar, Sengupta, Das and Kaw46, Reference Shaikh, Lad, Jana, Sarkar, Dey and Kumar47]. A linearly polarized probe laser beam becomes elliptically polarized owing to the Cotton–Mouton effect, and, by measuring the ellipticity
![]() $\unicode[STIX]{x1D6FD}$
, the
$\unicode[STIX]{x1D6FD}$
, the
![]() $B$
-field can be estimated by solving the equation
$B$
-field can be estimated by solving the equation
where
![]() $l$
is the path length traversed by the probe laser beam inside the plasma. In contrast to the Faraday effect, the Cotton–Mouton effect detects the
$l$
is the path length traversed by the probe laser beam inside the plasma. In contrast to the Faraday effect, the Cotton–Mouton effect detects the
![]() $B$
-field perpendicular to the direction of propagation of the probe beam.
$B$
-field perpendicular to the direction of propagation of the probe beam.
Additional measurements of the plasma profile, especially the electron density profile
![]() $n_{e}(l)$
, are essential for accurate evaluation of the
$n_{e}(l)$
, are essential for accurate evaluation of the
![]() $B$
-field strength.
$B$
-field strength.
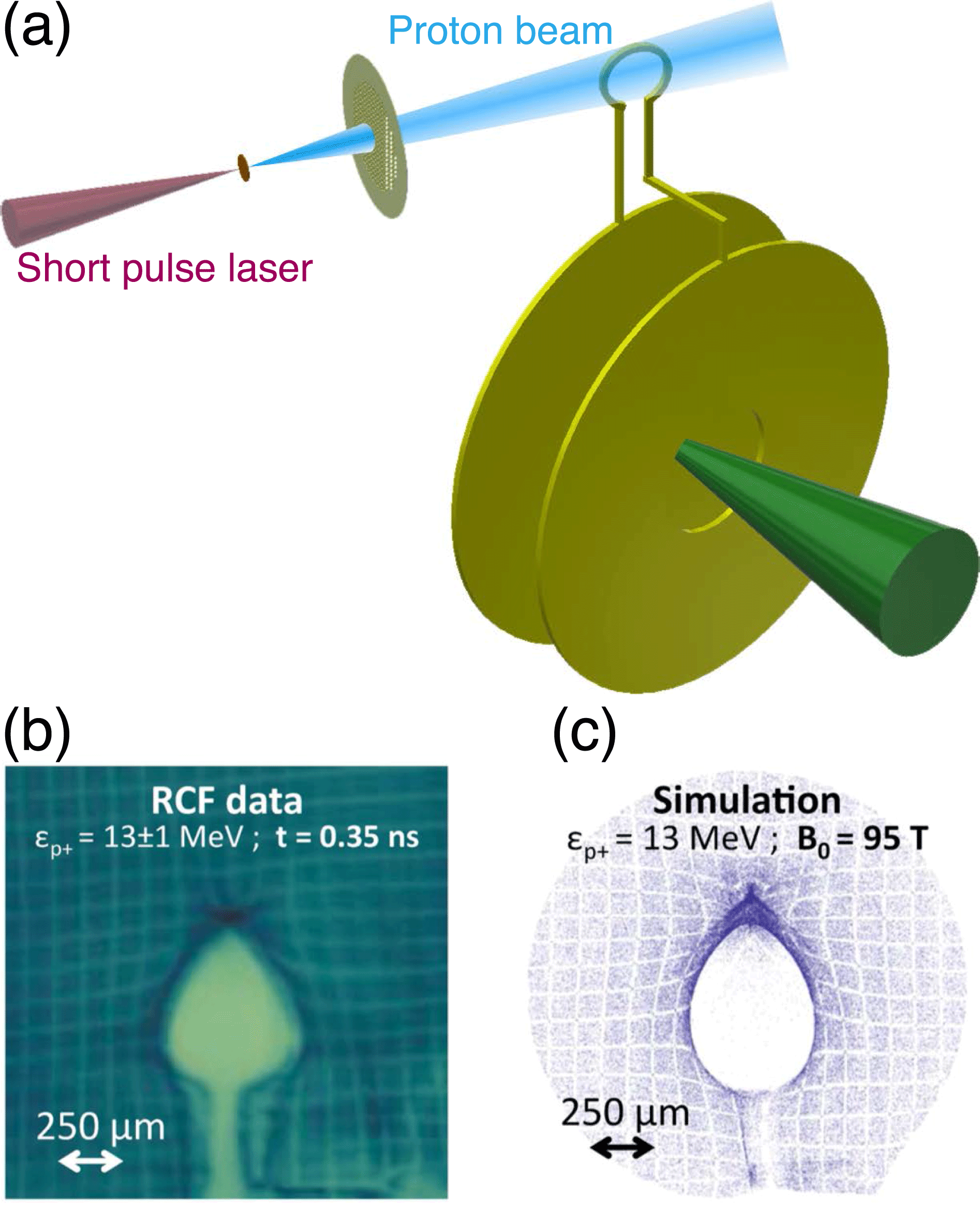
Figure 6. Example of a proton deflectometry measurement: (a) schematic of the setup; (b) image obtained on RCF with 13 MeV protons; (c) simulation of proton deflection in a
![]() $B$
-field[Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, D’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyè, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey35].
$B$
-field[Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, D’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyè, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey35].
3.3 Charged-particle deflectometry
With the target normal sheath acceleration (TNSA), it is easy to obtain high-energy proton beams with a cutoff energy of tens of MeV[Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely48, Reference Passoni, Bertagna and Zani49]. An alternative is to generate a monoenergetic proton beam as a product of nuclear fusion[Reference Li, Seguin, Frenje, Rygg, Petrasso, Town, Amendt, Hatchett, Landen, MacKinnon, Patel, Smalyuk, Sangster and Knauer23]. The protons are deflected by the Lorentz force while propagating through the magnetic coil region. An example of an experimental setting used by Santos et al.
[Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, D’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyè, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey35] is shown in Figure 6(a). The experiments were conducted at the LULI Pico 2000 laser facility with synchronized nanosecond and picosecond laser pulses. The nanosecond laser beam was focused on a CC target to generate a
![]() $B$
-field in the coil. A secondary target was positioned beside the coil, and TNSA proton beams directed toward the coil were driven by the picosecond laser. A mesh was placed between the secondary target and the coil to quantify the
$B$
-field in the coil. A secondary target was positioned beside the coil, and TNSA proton beams directed toward the coil were driven by the picosecond laser. A mesh was placed between the secondary target and the coil to quantify the
![]() $B$
-field. Figure 6(b) shows an image of proton deflectometry achieved with 13 MeV protons. The deformation of the mesh shadow and a bulb shape at the coil can be clearly seen. Figure 6(c) shows the result of a three-dimensional Monte Carlo simulation of the trajectories of 13 MeV protons through the coil. By comparing the experimentally obtained proton image with the simulation results, information about the
$B$
-field. Figure 6(b) shows an image of proton deflectometry achieved with 13 MeV protons. The deformation of the mesh shadow and a bulb shape at the coil can be clearly seen. Figure 6(c) shows the result of a three-dimensional Monte Carlo simulation of the trajectories of 13 MeV protons through the coil. By comparing the experimentally obtained proton image with the simulation results, information about the
![]() $B$
-field can be derived. Proton deflectometry allows direct measurement of the
$B$
-field can be derived. Proton deflectometry allows direct measurement of the
![]() $B$
-field in the coil region, with spatial and temporal resolutions being obtained in a single shot. The spatial resolution is found by recording a two-dimensional deflection pattern with radiochromic film (RCF) stacks. Protons are stopped at different layers in the RCF, with each layer corresponding to a specific proton energy. By taking into account the time of flight between the proton source and the coil, the pattern on each RCF layer represents the
$B$
-field in the coil region, with spatial and temporal resolutions being obtained in a single shot. The spatial resolution is found by recording a two-dimensional deflection pattern with radiochromic film (RCF) stacks. Protons are stopped at different layers in the RCF, with each layer corresponding to a specific proton energy. By taking into account the time of flight between the proton source and the coil, the pattern on each RCF layer represents the
![]() $B$
-field at different times. Evaluations of the strength of a laser-driven
$B$
-field at different times. Evaluations of the strength of a laser-driven
![]() $B$
-field using proton deflectometry have been reported previously by Li et al.
[Reference Li, Seguin, Frenje, Rygg, Petrasso, Town, Amendt, Hatchett, Landen, MacKinnon, Patel, Smalyuk, Sangster and Knauer23, Reference Li, Seguin, Frenje, Rosenberg, Petrasso, Amendt, Koch, Landen, Park, Robey, Town, Casner, Philippe, Betti, Knauer, Meyerhofer, Back, Kilkenny and Nikroo50] and have been applied on a coil target by Santos et al.
[Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, D’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyè, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey35], Zhu et al.
[Reference Zhu, Li, Yuan, Li, Li, Liao, Zhao, Zhong, Xue, He, Wang, Lu, Zhang, Yang, Zhou, Xie, Hong, Wei, Zhang, Han, Pei, Liu, Zhang, Zhu, Gu, Zhao, Zhang, Zhao and Zhang38], Gao et al.
[Reference Gao, Ji, Fiksel, Fox, Evans and Alfonso36], Law et al.
[Reference Law, Bailly-Grandvaux, Morace, Sakata, Matsuo, Kojima, Lee, Vaisseau, Arikawa, Yogo, Kondo, Zhang, Bellei, Santos, Fujioka and Azechi34] and Goyon et al.
[Reference Goyon, Pollock, Turnbull, Hazi, Divol, Farmer, Haberberger, Javedani, Johnson, Kemp, Levy, Grant Logan, Mariscal, Landen, Patankar, Ross, Rubenchik, Swadling, Williams, Fujioka, Law and Moody37].
$B$
-field using proton deflectometry have been reported previously by Li et al.
[Reference Li, Seguin, Frenje, Rygg, Petrasso, Town, Amendt, Hatchett, Landen, MacKinnon, Patel, Smalyuk, Sangster and Knauer23, Reference Li, Seguin, Frenje, Rosenberg, Petrasso, Amendt, Koch, Landen, Park, Robey, Town, Casner, Philippe, Betti, Knauer, Meyerhofer, Back, Kilkenny and Nikroo50] and have been applied on a coil target by Santos et al.
[Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, D’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyè, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey35], Zhu et al.
[Reference Zhu, Li, Yuan, Li, Li, Liao, Zhao, Zhong, Xue, He, Wang, Lu, Zhang, Yang, Zhou, Xie, Hong, Wei, Zhang, Han, Pei, Liu, Zhang, Zhu, Gu, Zhao, Zhang, Zhao and Zhang38], Gao et al.
[Reference Gao, Ji, Fiksel, Fox, Evans and Alfonso36], Law et al.
[Reference Law, Bailly-Grandvaux, Morace, Sakata, Matsuo, Kojima, Lee, Vaisseau, Arikawa, Yogo, Kondo, Zhang, Bellei, Santos, Fujioka and Azechi34] and Goyon et al.
[Reference Goyon, Pollock, Turnbull, Hazi, Divol, Farmer, Haberberger, Javedani, Johnson, Kemp, Levy, Grant Logan, Mariscal, Landen, Patankar, Ross, Rubenchik, Swadling, Williams, Fujioka, Law and Moody37].
As well as protons, high-energy electrons can be employed in deflectometry measurements. The energies of laser wakefield accelerated electrons can reach hundreds of MeV and even the GeV level[Reference Mirzaie, Li, Zeng, Hafz, Chen, Li, Zhu, Liao, Sokollik, Liu, Ma, Chen, Sheng and Zhang51], and, under particular conditions, a monoenergetic electron beam can be obtained[Reference Mangles, Murphy, Najmudin and Thomas52]. Such electron beams provide a powerful diagnostic tool for
![]() $B$
-fields. The Larmor radius for a relativistic electron in the presence of a
$B$
-fields. The Larmor radius for a relativistic electron in the presence of a
![]() $B$
-field is
$B$
-field is
where
![]() $\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D6FE}$
,
![]() $m_{e}$
,
$m_{e}$
,
![]() $v_{\bot }$
and
$v_{\bot }$
and
![]() $q$
are the Lorentz factor, electron mass, component of velocity perpendicular to the
$q$
are the Lorentz factor, electron mass, component of velocity perpendicular to the
![]() $B$
-field and electron charge, respectively. The minimum requirement for the electron energy can be approximately estimated by limiting the region of nonzero
$B$
-field and electron charge, respectively. The minimum requirement for the electron energy can be approximately estimated by limiting the region of nonzero
![]() $B$
-field, of dimension
$B$
-field, of dimension
![]() $R$
, to be smaller than
$R$
, to be smaller than
![]() $r_{L}$
. In Figure 7, the minimum electron energy is shown as a function of the product of
$r_{L}$
. In Figure 7, the minimum electron energy is shown as a function of the product of
![]() $B$
-field strength and the extent of the
$B$
-field strength and the extent of the
![]() $B$
-field,
$B$
-field,
![]() $B\cdot R$
in units of T
$B\cdot R$
in units of T
![]() $\cdot$
mm. As expected, to measure a large
$\cdot$
mm. As expected, to measure a large
![]() $B$
-field with a large spatial range, a higher electron energy is needed.
$B$
-field with a large spatial range, a higher electron energy is needed.
4 Applications
We present here some typical applications of laser-driven coils to generate strong
![]() $B$
-fields for laboratory studies.
$B$
-fields for laboratory studies.
4.1 Low-
 $\unicode[STIX]{x1D6FD}$
magnetic reconnection
$\unicode[STIX]{x1D6FD}$
magnetic reconnection
Magnetic reconnection is an important process in many astrophysical phenomena, including solar flares, star formation and auroras, and there have been a number of laboratory investigations based on laser–plasma interactions[Reference Nilson, Willingale, Kaluza, Kamperidis, Minardi, Wei, Fernandes, Notley, Bandyopadhyay, Sherlock, Kingham, Tatarakis, Najmudin, Rozmus, Evans, Haines, Dangor and Krushelnick7, Reference Zhong, Li, Wang, Wang, Dong, Xiao, Wang, Liu, Zhang, An, Wang, Zhu, Gu, He, Zhao and Zhang8]. To mimic the conditions of low-
![]() $\unicode[STIX]{x1D6FD}$
magnetic reconnection (where
$\unicode[STIX]{x1D6FD}$
magnetic reconnection (where
![]() $\unicode[STIX]{x1D6FD}$
is the ratio of plasma pressure to magnetic pressure), it is necessary to apply a
$\unicode[STIX]{x1D6FD}$
is the ratio of plasma pressure to magnetic pressure), it is necessary to apply a
![]() $B$
-field to a low-density plasma. Pei et al.
[Reference Pei, Zhong, Sakawa, Zhang, Zhang, Wei, Li, Li, Zhu, Sano, Hara, Kondo, Fujioka, Liang, Wang and Zhao33] used a double-U-turn coil for this purpose, with an antiparallel
$B$
-field to a low-density plasma. Pei et al.
[Reference Pei, Zhong, Sakawa, Zhang, Zhang, Wei, Li, Li, Zhu, Sano, Hara, Kondo, Fujioka, Liang, Wang and Zhao33] used a double-U-turn coil for this purpose, with an antiparallel
![]() $B$
-field being generated between the two coils. Heating by the current in the coil and by X-rays from the laser ablation leads to the creation of a low-density plasma, which then flows into the
$B$
-field being generated between the two coils. Heating by the current in the coil and by X-rays from the laser ablation leads to the creation of a low-density plasma, which then flows into the
![]() $B$
-field. Low-
$B$
-field. Low-
![]() $\unicode[STIX]{x1D6FD}$
magnetic reconnection can occur under these conditions.
$\unicode[STIX]{x1D6FD}$
magnetic reconnection can occur under these conditions.
4.2 Collimation of relativistic electron beams
A collimated relativistic electron beam (REB) is useful for many applications, but the REBs produced by intense laser interaction with a solid target are usually strongly divergent. Simulations have shown that a kilotesla external
![]() $B$
-field could effectively decrease the angle of divergence of the REB[Reference Cai, Zhu and He16]. Such collimated REBs have been experimentally investigated by Bailly-Grandvaux et al.
[Reference Bailly-Grandvaux, Santos, Bellei, Forestier-Colleoni, Fujioka, Giuffrida, Honrubia, Batani, Bouillaud, Chevrot, Cross, Crowston, Dorard, Dubois, Ehret, Gregori, Hulin, Kojima, Loyez, Marquès, Morace, Nicolaï, Roth, Sakata, Schaumann, Serres, Servel, Tikhonchuk, Woolsey and Zhang20].
$B$
-field could effectively decrease the angle of divergence of the REB[Reference Cai, Zhu and He16]. Such collimated REBs have been experimentally investigated by Bailly-Grandvaux et al.
[Reference Bailly-Grandvaux, Santos, Bellei, Forestier-Colleoni, Fujioka, Giuffrida, Honrubia, Batani, Bouillaud, Chevrot, Cross, Crowston, Dorard, Dubois, Ehret, Gregori, Hulin, Kojima, Loyez, Marquès, Morace, Nicolaï, Roth, Sakata, Schaumann, Serres, Servel, Tikhonchuk, Woolsey and Zhang20].
4.3 MHD
Matsuo et al.
[Reference Matsuo, Nagatomo, Zhang, Nicolaï, Sano, Sakata, Kojima, Lee, Law, Arikawa, Sakawa, Morita, Kuramitsu, Fujioka and Azechi12] applied a pair of CC targets to generate a quasi-uniform
![]() $B$
-field of a few hundred tesla in a laser-produced plasma. By adding a secondary laser-ablated sample in the
$B$
-field of a few hundred tesla in a laser-produced plasma. By adding a secondary laser-ablated sample in the
![]() $B$
-field, the MHD properties of the plasma were studied. Electron thermal conduction in the external
$B$
-field, the MHD properties of the plasma were studied. Electron thermal conduction in the external
![]() $B$
-field was found to be strongly affected, leading to velocity changes in the ablated plasma. The results also indicated that the growth of hydrodynamic perturbations was also affected by the external
$B$
-field was found to be strongly affected, leading to velocity changes in the ablated plasma. The results also indicated that the growth of hydrodynamic perturbations was also affected by the external
![]() $B$
-field as a result of the anisotropic thermal conductivity in the ablated plasma.
$B$
-field as a result of the anisotropic thermal conductivity in the ablated plasma.
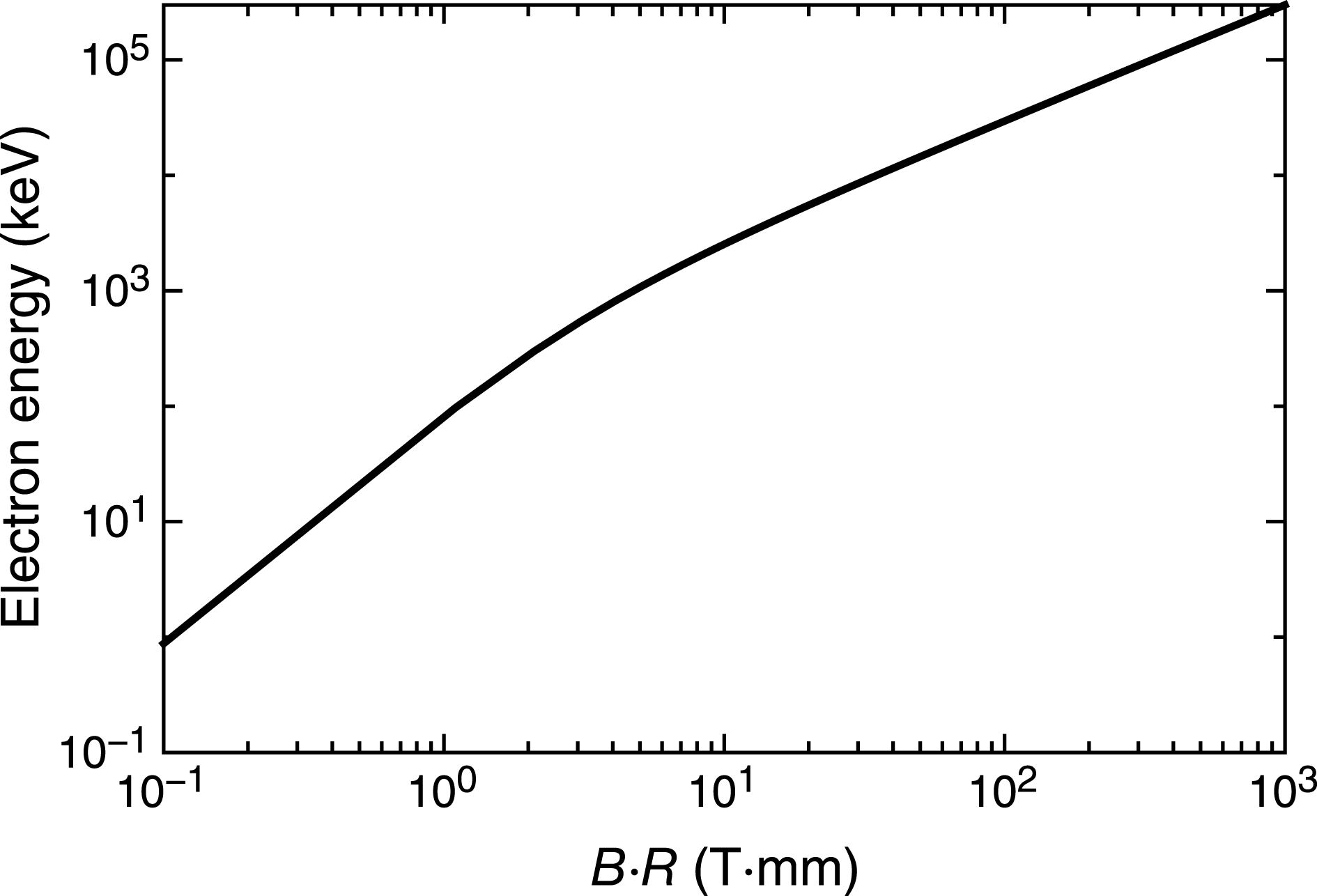
Figure 7. Minimum electron energy required for electron deflectometry, as a function of the product
![]() $B\cdot R$
.
$B\cdot R$
.
5 Conclusions
The use of laser-driven coils is an important method to provide a strong
![]() $B$
-field at a sub-kilotesla to a kilotesla level. In addition to the high field strength achievable, the controllability of generation and accessibility of a secondary sample are other advantages of this scheme. The strength, space and time ranges of the
$B$
-field at a sub-kilotesla to a kilotesla level. In addition to the high field strength achievable, the controllability of generation and accessibility of a secondary sample are other advantages of this scheme. The strength, space and time ranges of the
![]() $B$
-field could be further optimized depending on the desired application through appropriate choices of incident laser, target and coil shapes. This scheme could provide a new test bed for a range of laboratory applications including, but not limited to, HEDP, laboratory astrophysics, fusion research and laser particle acceleration. Many types of target have been tested under different laser conditions. There are also some other advanced designs for generation of strong
$B$
-field could be further optimized depending on the desired application through appropriate choices of incident laser, target and coil shapes. This scheme could provide a new test bed for a range of laboratory applications including, but not limited to, HEDP, laboratory astrophysics, fusion research and laser particle acceleration. Many types of target have been tested under different laser conditions. There are also some other advanced designs for generation of strong
![]() $B$
-fields using short-pulse lasers, such as the snail-shaped target proposed by Korneev et al.
[Reference Korneev, D’Humières and Tikhonchuk53].
$B$
-fields using short-pulse lasers, such as the snail-shaped target proposed by Korneev et al.
[Reference Korneev, D’Humières and Tikhonchuk53].
Acknowledgements
This study was supported in part by the Science Challenge Project (No. TZ2016005), the CAS-JSPS Joint Research Program (External Cooperation Program of the BIC, Chinese Academy of Sciences, No. 112111KYSB20160015), the National Natural Science Foundation of China (Nos. 11520101003, 11535001 and 11861121001) and the Strategic Priority Research Program of the Chinese Academy of Sciences (Nos. XDB16010200 and XDB07030300).












