1 Introduction
Laser–solid interactions have been widely investigated in recent decades because of their wide applications, such as charged particle acceleration[Reference Brunel1–Reference Pukhov5] and radiation generation[Reference Pan, Zheng, Wu and He6–Reference Ridgers, Brady, Duclous, Kirk, Bennett, Arber, Robinson and Bell14]. For example, the vacuum heating mechanism and
![]() $\mathbf{J}\times \mathbf{B}$
heating mechanism[Reference Cai, Yu, Zhu and Zheng2] can be used to accelerate electrons. Also, the radiation pressure acceleration (RPA) mechanism[Reference Yan, Lin, Sheng, Guo, Liu, Lu, Fang and Chen15–Reference Steinke, Hilz, Schnürer, Priebe, Bränzel, Abicht, Kiefer, Kreuzer, Ostermayr, Schreiber, Andreev, Yu, Pukhov and Sandner18] or the breakout afterburner (BOA) mechanism[Reference Yin, Albright, Bowers, Jung, Fernández and Hegelich19–Reference Jung, Yin, Albright, Gautier, Letzring, Dromey, Yeung, Hörlein, Shah, Palaniyappan, Allinger, Schreiber, Bowers, Wu, Fernandez, Habs and Hegelich22] can be used to efficiently accelerate protons or even heavy ions. It is shown that the most efficient target thickness for RPA or BOA is
$\mathbf{J}\times \mathbf{B}$
heating mechanism[Reference Cai, Yu, Zhu and Zheng2] can be used to accelerate electrons. Also, the radiation pressure acceleration (RPA) mechanism[Reference Yan, Lin, Sheng, Guo, Liu, Lu, Fang and Chen15–Reference Steinke, Hilz, Schnürer, Priebe, Bränzel, Abicht, Kiefer, Kreuzer, Ostermayr, Schreiber, Andreev, Yu, Pukhov and Sandner18] or the breakout afterburner (BOA) mechanism[Reference Yin, Albright, Bowers, Jung, Fernández and Hegelich19–Reference Jung, Yin, Albright, Gautier, Letzring, Dromey, Yeung, Hörlein, Shah, Palaniyappan, Allinger, Schreiber, Bowers, Wu, Fernandez, Habs and Hegelich22] can be used to efficiently accelerate protons or even heavy ions. It is shown that the most efficient target thickness for RPA or BOA is
![]() $l_{0}=a_{0}\unicode[STIX]{x1D706}_{0}n_{c}/2\unicode[STIX]{x1D70B}n_{e}$
, where
$l_{0}=a_{0}\unicode[STIX]{x1D706}_{0}n_{c}/2\unicode[STIX]{x1D70B}n_{e}$
, where
![]() $a_{0}=eE_{0}/m_{e}\unicode[STIX]{x1D714}_{0}c$
is the normalized vector potential,
$a_{0}=eE_{0}/m_{e}\unicode[STIX]{x1D714}_{0}c$
is the normalized vector potential,
![]() $m_{e}$
and
$m_{e}$
and
![]() $e$
are the electron mass and charge,
$e$
are the electron mass and charge,
![]() $\unicode[STIX]{x1D706}_{0}$
and
$\unicode[STIX]{x1D706}_{0}$
and
![]() $\unicode[STIX]{x1D714}_{0}$
are the laser wavelength and frequency,
$\unicode[STIX]{x1D714}_{0}$
are the laser wavelength and frequency,
![]() $n_{c}=m_{e}\unicode[STIX]{x1D714}_{0}^{2}/4\unicode[STIX]{x1D70B}e^{2}$
is the critical density and
$n_{c}=m_{e}\unicode[STIX]{x1D714}_{0}^{2}/4\unicode[STIX]{x1D70B}e^{2}$
is the critical density and
![]() $n_{e}$
is the electron density of the solid. For example, for
$n_{e}$
is the electron density of the solid. For example, for
![]() $a_{0}=5$
and
$a_{0}=5$
and
![]() $n_{e}=50n_{c}$
, the optimal thickness is only about
$n_{e}=50n_{c}$
, the optimal thickness is only about
![]() $0.016\unicode[STIX]{x1D706}_{0}$
, and so thin a target cannot absorb much of the laser energy. As to the radiation generation by laser–solid interactions, synchrotron radiation[Reference Pan, Zheng, Wu and He6–Reference Pan, Zheng, Wu, Cao, Liu and He8] and high-order harmonic generation[Reference an der Brügge and Pukhov23–Reference Dromey, Cousens, Rykovanov, Yeung, Jung, Gautier, Dzelzainis, Kiefer, Palaniyppan, Shah, Schreiber, Fernandez, Lewis, Zepf and Hegelich25] are always useful mechanisms. Synchrotron radiation generated by laser–solid interactions may have a high energy conversion efficiency. Some previous works have reported that even more than 40% of the laser energy could be converted into radiation energy[Reference Ji, Pukhov, Nerush, Kostyukov, Shen and Akli26]. However, such a high energy conversion efficiency needs a super-intense laser, which is not achievable in the laboratory at present. When the laser intensity is low, the energy conversion efficiency is also low. As to the high-order harmonics generated by laser–solid interactions, it is known that the laser can only penetrate to the skin depth, so only a few electrons will participate in the radiation process and the energy conversion efficiency from the laser to the radiation is also very low. Researchers have made efforts to improve the energy conversion efficiency of the laser–solid interactions. Fortunately, using a periodic structure on the target surface is possibly one of the best choices. It is shown in Refs. [Reference Wang, Sheng and Zhang27, Reference Kahaly, Yadav, Wang, Sengupta, Sheng, Das, Kaw and Ravindra Kumar28] that nearly 100% light absorption occurs when the laser interacts with a subwavelength grating target. In addition, the pre-structured target can also be used to generate high-order harmonics propagating along the target surface[Reference Zhang, Chen, Liu, Yuan, Weng, Zheng, Ma, Shao, Sheng and Zhang29], which are the so-called surface plasma waves. These surface plasma waves can also influence the high-order harmonic generation[Reference Cantono, Fedeli, Sgattoni, Denoeud, Chopineau, Réau, Ceccotti and Macchi30] and the electron transportation to the target back surface, and it is shown in Ref. [Reference Pan, Zheng, Cao, Liu and He31] that, when the laser is obliquely incident, attosecond electron bunches will be generated on the target back surface.
$0.016\unicode[STIX]{x1D706}_{0}$
, and so thin a target cannot absorb much of the laser energy. As to the radiation generation by laser–solid interactions, synchrotron radiation[Reference Pan, Zheng, Wu and He6–Reference Pan, Zheng, Wu, Cao, Liu and He8] and high-order harmonic generation[Reference an der Brügge and Pukhov23–Reference Dromey, Cousens, Rykovanov, Yeung, Jung, Gautier, Dzelzainis, Kiefer, Palaniyppan, Shah, Schreiber, Fernandez, Lewis, Zepf and Hegelich25] are always useful mechanisms. Synchrotron radiation generated by laser–solid interactions may have a high energy conversion efficiency. Some previous works have reported that even more than 40% of the laser energy could be converted into radiation energy[Reference Ji, Pukhov, Nerush, Kostyukov, Shen and Akli26]. However, such a high energy conversion efficiency needs a super-intense laser, which is not achievable in the laboratory at present. When the laser intensity is low, the energy conversion efficiency is also low. As to the high-order harmonics generated by laser–solid interactions, it is known that the laser can only penetrate to the skin depth, so only a few electrons will participate in the radiation process and the energy conversion efficiency from the laser to the radiation is also very low. Researchers have made efforts to improve the energy conversion efficiency of the laser–solid interactions. Fortunately, using a periodic structure on the target surface is possibly one of the best choices. It is shown in Refs. [Reference Wang, Sheng and Zhang27, Reference Kahaly, Yadav, Wang, Sengupta, Sheng, Das, Kaw and Ravindra Kumar28] that nearly 100% light absorption occurs when the laser interacts with a subwavelength grating target. In addition, the pre-structured target can also be used to generate high-order harmonics propagating along the target surface[Reference Zhang, Chen, Liu, Yuan, Weng, Zheng, Ma, Shao, Sheng and Zhang29], which are the so-called surface plasma waves. These surface plasma waves can also influence the high-order harmonic generation[Reference Cantono, Fedeli, Sgattoni, Denoeud, Chopineau, Réau, Ceccotti and Macchi30] and the electron transportation to the target back surface, and it is shown in Ref. [Reference Pan, Zheng, Cao, Liu and He31] that, when the laser is obliquely incident, attosecond electron bunches will be generated on the target back surface.
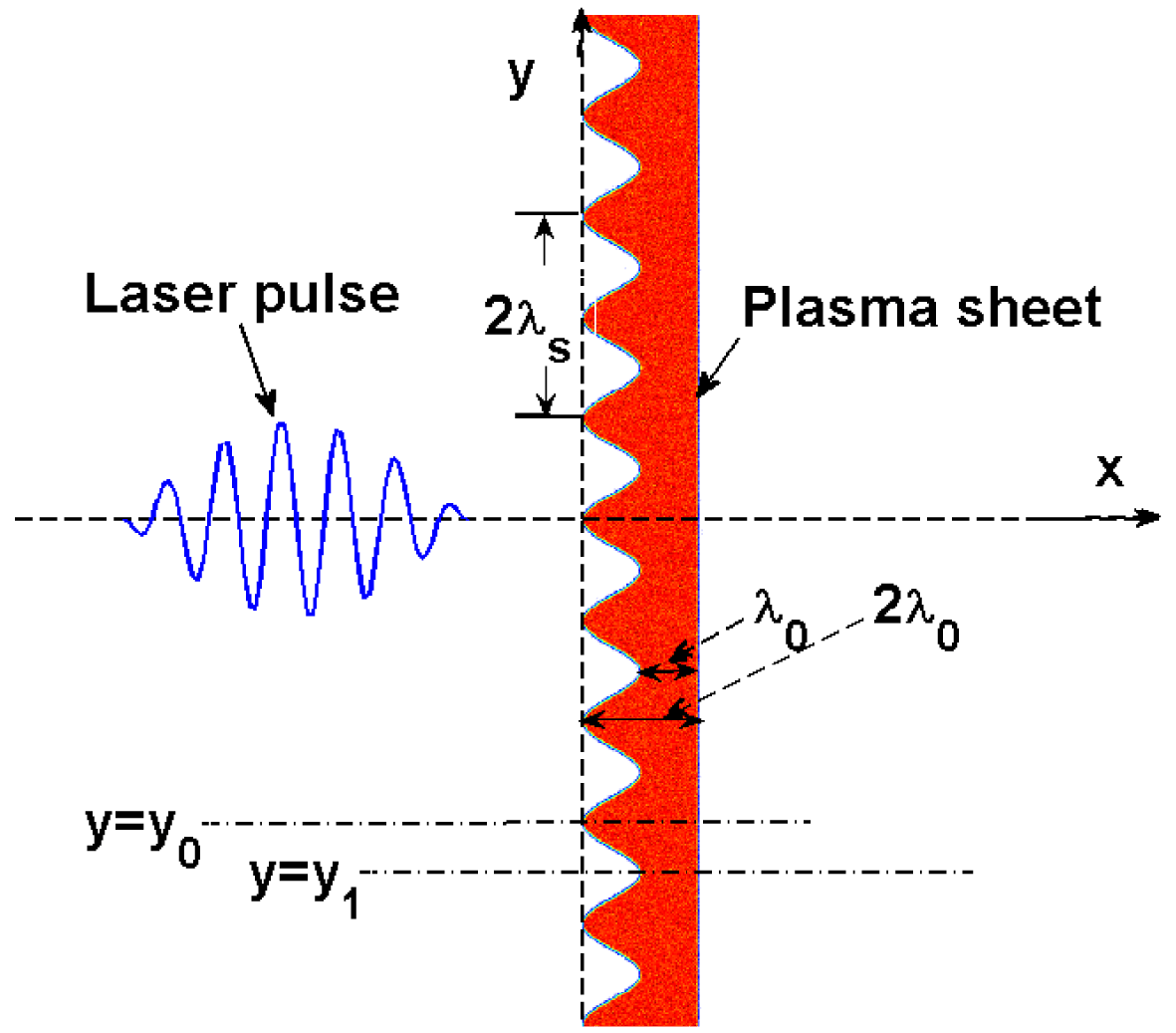
Figure 1. Scheme of the pre-structured target and the p-polarized laser pulse. The laser is normally incident, and the structure period and depth are both
![]() $\unicode[STIX]{x1D706}_{0}$
, where
$\unicode[STIX]{x1D706}_{0}$
, where
![]() $\unicode[STIX]{x1D706}_{0}$
is the laser wavelength.
$\unicode[STIX]{x1D706}_{0}$
is the laser wavelength.
In this paper, with the help of two-dimensional (2D) and three-dimensional (3D) particle-in-cell (PIC) simulations, we investigate the interactions between normally incident intense laser pulses and ultra-thin plasma sheets with densities much larger than the relativistically critical density
![]() $\unicode[STIX]{x1D6FE}_{0}n_{c}$
and thicknesses much larger than the skin depth
$\unicode[STIX]{x1D6FE}_{0}n_{c}$
and thicknesses much larger than the skin depth
![]() $l_{s}=c/\unicode[STIX]{x1D714}_{pe}$
. Both flat targets and pre-structured targets are used in our simulations. The pre-structured target is shown in Figure 1. The structure period is
$l_{s}=c/\unicode[STIX]{x1D714}_{pe}$
. Both flat targets and pre-structured targets are used in our simulations. The pre-structured target is shown in Figure 1. The structure period is
![]() $\unicode[STIX]{x1D706}_{s}=\unicode[STIX]{x1D706}_{0}$
, which satisfies the matching condition of the surface plasma wave (SPW) excitation for normal incidence[Reference Bigongiari, Raynaud, Riconda and Héron32]. The thickness of the flat target is also
$\unicode[STIX]{x1D706}_{s}=\unicode[STIX]{x1D706}_{0}$
, which satisfies the matching condition of the surface plasma wave (SPW) excitation for normal incidence[Reference Bigongiari, Raynaud, Riconda and Héron32]. The thickness of the flat target is also
![]() $\unicode[STIX]{x1D706}_{0}$
. The simulation results show that part of the laser energy will penetrate through both targets for both the laser’s fundamental frequency and its high-order harmonics. However, compared to the flat target, the transmitted laser energy behind the pre-structured target is increased by about two orders of magnitude. The intensity of the high-order harmonics behind the pre-structured target is also much larger. Further analysis shows that the fundamental emission, which was also observed experimentally[Reference Eidmann, Kawachi, Marcinkevičius, Bartlome, Tsakiris and Witte33], is emitted by electron bunches on the target rear surface.
$\unicode[STIX]{x1D706}_{0}$
. The simulation results show that part of the laser energy will penetrate through both targets for both the laser’s fundamental frequency and its high-order harmonics. However, compared to the flat target, the transmitted laser energy behind the pre-structured target is increased by about two orders of magnitude. The intensity of the high-order harmonics behind the pre-structured target is also much larger. Further analysis shows that the fundamental emission, which was also observed experimentally[Reference Eidmann, Kawachi, Marcinkevičius, Bartlome, Tsakiris and Witte33], is emitted by electron bunches on the target rear surface.
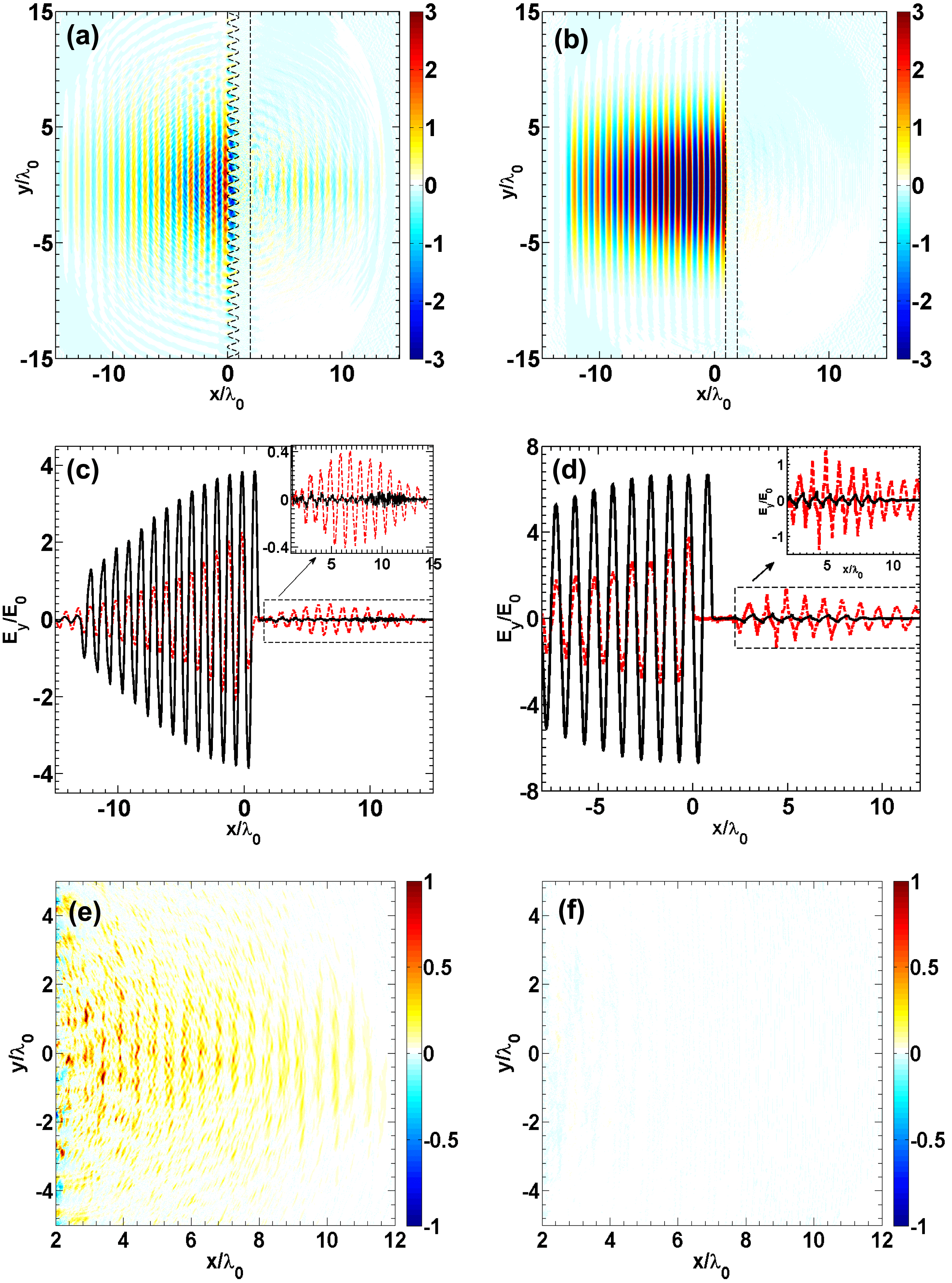
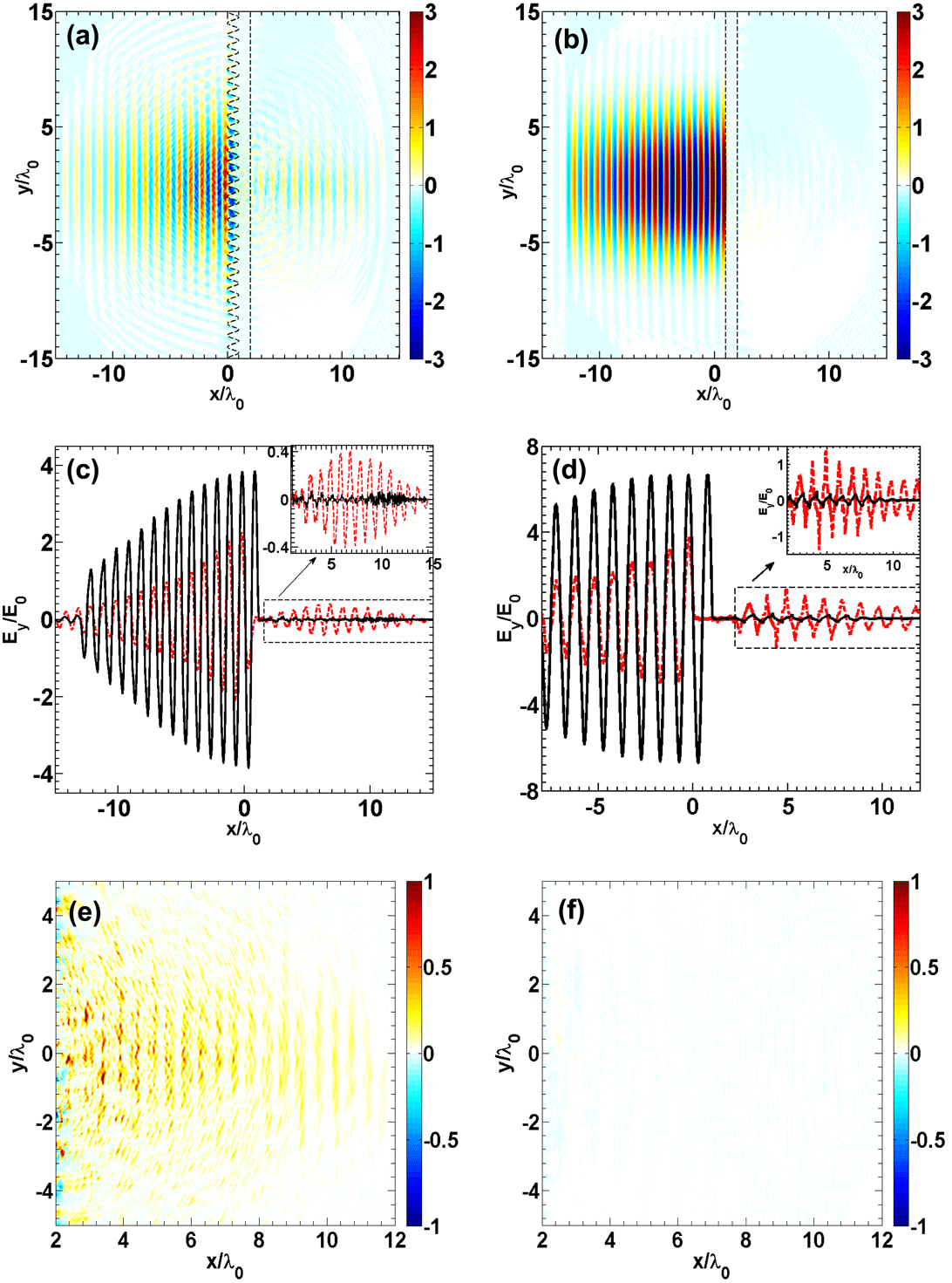
Figure 2. The electric field
![]() $E_{y}$
and the Poynting flux
$E_{y}$
and the Poynting flux
![]() $S_{x}=E_{y}B_{z}$
at
$S_{x}=E_{y}B_{z}$
at
![]() $t=30T_{0}$
(
$t=30T_{0}$
(
![]() $t=25T_{0}$
for (d)). (a) and (b) are the distributions of
$t=25T_{0}$
for (d)). (a) and (b) are the distributions of
![]() $E_{y}$
for the pre-structured and flat targets, respectively. (c) and (d) are the distributions along the
$E_{y}$
for the pre-structured and flat targets, respectively. (c) and (d) are the distributions along the
![]() $x$
axis for the pre-structured and flat targets, respectively. (e) and (f) are the distributions of
$x$
axis for the pre-structured and flat targets, respectively. (e) and (f) are the distributions of
![]() $S_{x}$
behind the target for the pre-structured and flat targets, respectively. In (a)–(c), (e) and (f), the laser normalized vector potential is
$S_{x}$
behind the target for the pre-structured and flat targets, respectively. In (a)–(c), (e) and (f), the laser normalized vector potential is
![]() $a_{0}=3$
and the electron density is
$a_{0}=3$
and the electron density is
![]() $n_{e}=25n_{c}$
. In (d), the laser normalized vector potential is
$n_{e}=25n_{c}$
. In (d), the laser normalized vector potential is
![]() $a_{0}=5$
and the electron density is
$a_{0}=5$
and the electron density is
![]() $n_{e}=900n_{c}$
. In (c) and (d), the red dashed line and the black solid line represent the pre-structured and flat target cases, respectively. In this figure,
$n_{e}=900n_{c}$
. In (c) and (d), the red dashed line and the black solid line represent the pre-structured and flat target cases, respectively. In this figure,
![]() $E_{0}=m_{e}\unicode[STIX]{x1D714}_{0}c/e\approx 3.22\times 10^{12}~\text{V}/\text{m}$
. The electric fields in (a) and (b) are both normalized by
$E_{0}=m_{e}\unicode[STIX]{x1D714}_{0}c/e\approx 3.22\times 10^{12}~\text{V}/\text{m}$
. The electric fields in (a) and (b) are both normalized by
![]() $E_{0}$
.
$E_{0}$
.
2 Enhancement of the transmitted laser energy and the transmitted high-order harmonics
The pre-structured targets used in our work have been applied in many previous works[Reference Pan, Zheng, Wu, Cao, Liu and He8, Reference Cerchez, Giesecke, Peth, Toncian, Albertazzi, Fuchs, Willi and Toncian12, Reference Bigongiari, Raynaud, Riconda and Héron32, Reference Bigongiari, Raynaud, Riconda, Héron and Macchi34–Reference Bargsten, Hollinger, Capeluto, Kaymak, Pukhov, Wang, Rockwood, Wang, Keiss, Tommasini, London, Park, Busquet, Klapisch, Shlyaptsev and Rocca38]. A very important application of the pre-structured target is to excite SPWs. Since the SPW excitation is also important for our work, we first give the matching condition for SPW excitation, which is sin
![]() $\unicode[STIX]{x1D703}+\unicode[STIX]{x1D706}_{0}/\unicode[STIX]{x1D706}_{s}\approx 1$
[Reference Bigongiari, Raynaud, Riconda and Héron32, Reference Bigongiari, Raynaud, Riconda, Héron and Macchi34], where
$\unicode[STIX]{x1D703}+\unicode[STIX]{x1D706}_{0}/\unicode[STIX]{x1D706}_{s}\approx 1$
[Reference Bigongiari, Raynaud, Riconda and Héron32, Reference Bigongiari, Raynaud, Riconda, Héron and Macchi34], where
![]() $\unicode[STIX]{x1D706}_{s}$
is the structure period and
$\unicode[STIX]{x1D706}_{s}$
is the structure period and
![]() $\unicode[STIX]{x1D703}$
is the laser incidence angle. This condition is valid for an overdense (
$\unicode[STIX]{x1D703}$
is the laser incidence angle. This condition is valid for an overdense (
![]() $n_{e}\gg n_{c}$
) cold plasma. The target shown in Figure 1 is also an overdense cold plasma, so the structure period is
$n_{e}\gg n_{c}$
) cold plasma. The target shown in Figure 1 is also an overdense cold plasma, so the structure period is
![]() $\unicode[STIX]{x1D706}_{s}=\unicode[STIX]{x1D706}_{0}$
to make sure the SPW can be excited by the normally incident laser (
$\unicode[STIX]{x1D706}_{s}=\unicode[STIX]{x1D706}_{0}$
to make sure the SPW can be excited by the normally incident laser (
![]() $\unicode[STIX]{x1D703}=0$
). To make comparisons, 2D PIC simulations with both pre-structured targets and flat targets are performed. In the first two simulations, we use a p-polarized Gaussian laser pulse with a peak amplitude
$\unicode[STIX]{x1D703}=0$
). To make comparisons, 2D PIC simulations with both pre-structured targets and flat targets are performed. In the first two simulations, we use a p-polarized Gaussian laser pulse with a peak amplitude
![]() $a_{0}=3$
and duration
$a_{0}=3$
and duration
![]() $\unicode[STIX]{x1D70F}=20T_{0}$
, where
$\unicode[STIX]{x1D70F}=20T_{0}$
, where
![]() $T_{0}$
is the laser period. The laser wavelength is
$T_{0}$
is the laser period. The laser wavelength is
![]() $\unicode[STIX]{x1D706}_{0}=1~\unicode[STIX]{x03BC}\text{m}$
. The electron densities for both the pre-structured target and the flat target are
$\unicode[STIX]{x1D706}_{0}=1~\unicode[STIX]{x03BC}\text{m}$
. The electron densities for both the pre-structured target and the flat target are
![]() $n_{e}=25n_{c}$
and the mass-to-charge ratio of the ion is set to 1836 (the unit is
$n_{e}=25n_{c}$
and the mass-to-charge ratio of the ion is set to 1836 (the unit is
![]() $m_{e}/e$
, meaning the ion is equivalent to a proton) to make sure that the ion motion is also taken into account. The electron temperature used in both cases is
$m_{e}/e$
, meaning the ion is equivalent to a proton) to make sure that the ion motion is also taken into account. The electron temperature used in both cases is
![]() $T_{e}=1$
keV. The amplitude of the target structure is
$T_{e}=1$
keV. The amplitude of the target structure is
![]() $\unicode[STIX]{x1D706}_{0}$
and the thinnest part of the pre-structured target is also
$\unicode[STIX]{x1D706}_{0}$
and the thinnest part of the pre-structured target is also
![]() $\unicode[STIX]{x1D706}_{0}$
, as well as its structure period. The simulation box is
$\unicode[STIX]{x1D706}_{0}$
, as well as its structure period. The simulation box is
![]() $40\unicode[STIX]{x1D706}_{0}\times 30\unicode[STIX]{x1D706}_{0}$
in the
$40\unicode[STIX]{x1D706}_{0}\times 30\unicode[STIX]{x1D706}_{0}$
in the
![]() $x$
and
$x$
and
![]() $y$
directions, with grid steps of
$y$
directions, with grid steps of
![]() $0.01\unicode[STIX]{x1D706}_{0}\times 0.01\unicode[STIX]{x1D706}_{0}$
for
$0.01\unicode[STIX]{x1D706}_{0}\times 0.01\unicode[STIX]{x1D706}_{0}$
for
![]() $n_{e}=25n_{c}$
. In each cell, there are 100 electrons and 100 ions. To verify the robustness of our mechanism, in the third and fourth simulations, the laser peak amplitude is increased to
$n_{e}=25n_{c}$
. In each cell, there are 100 electrons and 100 ions. To verify the robustness of our mechanism, in the third and fourth simulations, the laser peak amplitude is increased to
![]() $a_{0}=5$
and the plasma density is increased to
$a_{0}=5$
and the plasma density is increased to
![]() $n_{e}=900n_{c}$
. Since the plasma density is increased to
$n_{e}=900n_{c}$
. Since the plasma density is increased to
![]() $n_{e}=900n_{c}$
, to make sure that the grid step is still smaller than the skin depth
$n_{e}=900n_{c}$
, to make sure that the grid step is still smaller than the skin depth
![]() $l_{s}=c/\unicode[STIX]{x1D714}_{pe}$
, the grid steps are decreased to
$l_{s}=c/\unicode[STIX]{x1D714}_{pe}$
, the grid steps are decreased to
![]() $0.001\unicode[STIX]{x1D706}_{0}\times 0.002\unicode[STIX]{x1D706}_{0}$
in the
$0.001\unicode[STIX]{x1D706}_{0}\times 0.002\unicode[STIX]{x1D706}_{0}$
in the
![]() $x$
and
$x$
and
![]() $y$
directions. The simulation results are shown in Figures 2–4.
$y$
directions. The simulation results are shown in Figures 2–4.
Figure 2 shows information of
![]() $E_{y}$
and
$E_{y}$
and
![]() $S_{x}=E_{y}B_{z}$
for the first four simulations at
$S_{x}=E_{y}B_{z}$
for the first four simulations at
![]() $t=30T_{0}$
. In Figures 2(a)–2(c), 2(e) and 2(f), the electron density is
$t=30T_{0}$
. In Figures 2(a)–2(c), 2(e) and 2(f), the electron density is
![]() $n_{e}=25n_{c}$
and the laser has a normalized vector potential
$n_{e}=25n_{c}$
and the laser has a normalized vector potential
![]() $a_{0}=3$
. However, in Figure 2(d), the electron density is
$a_{0}=3$
. However, in Figure 2(d), the electron density is
![]() $n_{e}=900n_{c}$
and the laser normalized vector potential is
$n_{e}=900n_{c}$
and the laser normalized vector potential is
![]() $a_{0}=5$
. As is seen in Figures 2(a) and 2(b), part of the laser energy ‘penetrates’ through the pre-structured target but little laser energy is found behind the flat target, which correspond to the Poynting flux distributions shown in Figures 2(e) and 2(f), respectively. Further calculation shows that the total energy of the transmitted radiation behind the pre-structured target is about 3.4% of the laser energy. More details of the distribution of
$a_{0}=5$
. As is seen in Figures 2(a) and 2(b), part of the laser energy ‘penetrates’ through the pre-structured target but little laser energy is found behind the flat target, which correspond to the Poynting flux distributions shown in Figures 2(e) and 2(f), respectively. Further calculation shows that the total energy of the transmitted radiation behind the pre-structured target is about 3.4% of the laser energy. More details of the distribution of
![]() $E_{y}$
on the laser axis are shown in Figure 2(c). For the flat target (the black solid lines), almost all laser energy is reflected. However, for the pre-structured target, the peak amplitude of the transmitted radiation is more than 13% of the incident laser. The inserted figure in Figure 2(c) further shows that the intensity (
$E_{y}$
on the laser axis are shown in Figure 2(c). For the flat target (the black solid lines), almost all laser energy is reflected. However, for the pre-structured target, the peak amplitude of the transmitted radiation is more than 13% of the incident laser. The inserted figure in Figure 2(c) further shows that the intensity (
![]() $\propto E_{y}^{2}$
) of the transmitted radiation behind the pre-structured target is increased by about two orders of magnitude compared to the flat target. Figure 2(d) shows that, even if the electron density is increased to
$\propto E_{y}^{2}$
) of the transmitted radiation behind the pre-structured target is increased by about two orders of magnitude compared to the flat target. Figure 2(d) shows that, even if the electron density is increased to
![]() $n_{e}=900n_{c}$
, the enhancement of the transmitted energy is still valid. It is also shown that when the laser intensity is increased, the intensity of the transmitted radiation is also increased, as well as the percentage of the transmitted energy. When comparing the peaks of the black lines in Figures 2(c) and 2(d), one finds that when the electron density is
$n_{e}=900n_{c}$
, the enhancement of the transmitted energy is still valid. It is also shown that when the laser intensity is increased, the intensity of the transmitted radiation is also increased, as well as the percentage of the transmitted energy. When comparing the peaks of the black lines in Figures 2(c) and 2(d), one finds that when the electron density is
![]() $n_{e}=25n_{c}$
, the peak (near
$n_{e}=25n_{c}$
, the peak (near
![]() $x=10\unicode[STIX]{x1D706}_{0}$
) of the transmitted radiation is much more intense and its wavelength is also shorter (or its frequency is higher). For the laser and plasma parameters used, these high-order harmonics should be generated by the coherence synchrotron emission (CSE) mechanism or the wavebreaking-associated transmitted emission (WTE) mechanism[Reference Z.-Y., Cherednychek and Pukhov39]. It is known that the radiation generated by the CSE or WTE mechanisms will be filtered by the target when propagating to the target back surface. When
$x=10\unicode[STIX]{x1D706}_{0}$
) of the transmitted radiation is much more intense and its wavelength is also shorter (or its frequency is higher). For the laser and plasma parameters used, these high-order harmonics should be generated by the coherence synchrotron emission (CSE) mechanism or the wavebreaking-associated transmitted emission (WTE) mechanism[Reference Z.-Y., Cherednychek and Pukhov39]. It is known that the radiation generated by the CSE or WTE mechanisms will be filtered by the target when propagating to the target back surface. When
![]() $n_{e}=900n_{c}$
, harmonics with orders lower than 30 will be filtered and harmonics with orders higher than 30 will be very weak, or not even excited by a laser with such a low intensity. However, when
$n_{e}=900n_{c}$
, harmonics with orders lower than 30 will be filtered and harmonics with orders higher than 30 will be very weak, or not even excited by a laser with such a low intensity. However, when
![]() $n_{e}=25n_{c}$
, the lowest order of the transmitted harmonics is only 5, and it can be easily excited by the given laser. So the transmitted radiation behind a flat target with
$n_{e}=25n_{c}$
, the lowest order of the transmitted harmonics is only 5, and it can be easily excited by the given laser. So the transmitted radiation behind a flat target with
![]() $n_{e}=25n_{c}$
is much more intense.
$n_{e}=25n_{c}$
is much more intense.

Figure 3. Time-space evolution of
![]() $E_{y}$
and snapshots of the electron density distribution at
$E_{y}$
and snapshots of the electron density distribution at
![]() $t=30T_{0}$
for both targets. (a) is the evolution of
$t=30T_{0}$
for both targets. (a) is the evolution of
![]() $E_{y}$
on
$E_{y}$
on
![]() $y=y_{1}$
, (b) is the evolution of
$y=y_{1}$
, (b) is the evolution of
![]() $E_{y}$
on
$E_{y}$
on
![]() $y=y_{0}$
, (c) is the density on the pre-structured target and (d) is the density on the flat target. Here,
$y=y_{0}$
, (c) is the density on the pre-structured target and (d) is the density on the flat target. Here,
![]() $E_{y}$
is also normalized by
$E_{y}$
is also normalized by
![]() $E_{0}$
and the electron densities (normalized by
$E_{0}$
and the electron densities (normalized by
![]() $n_{c}$
) are on a logarithmic scale.
$n_{c}$
) are on a logarithmic scale.
To understand how the pre-structured target enhances the transmitted laser energy, we give more details of the propagation properties of
![]() $E_{y}$
in Figures 3(a) and 3(b), which show the time-space evolution of
$E_{y}$
in Figures 3(a) and 3(b), which show the time-space evolution of
![]() $E_{y}$
on two lines shown in Figure 1 (
$E_{y}$
on two lines shown in Figure 1 (
![]() $y=y_{1}$
, the thinnest part of the target, and
$y=y_{1}$
, the thinnest part of the target, and
![]() $y=y_{0}=y_{1}+\unicode[STIX]{x1D706}_{0}/2$
, the thickest part of the target). We firstly discuss the evolution of
$y=y_{0}=y_{1}+\unicode[STIX]{x1D706}_{0}/2$
, the thickest part of the target). We firstly discuss the evolution of
![]() $E_{y}$
on
$E_{y}$
on
![]() $y=y_{1}$
shown in Figure 2(a). We have four regions along the
$y=y_{1}$
shown in Figure 2(a). We have four regions along the
![]() $x$
axis. In region I (vacuum in front of the target, where
$x$
axis. In region I (vacuum in front of the target, where
![]() $x/\unicode[STIX]{x1D706}_{0}<0$
), the reflected laser is very weak compared to the incident laser, which shows the same result as Figure 2. In region II (valley of the structure, where
$x/\unicode[STIX]{x1D706}_{0}<0$
), the reflected laser is very weak compared to the incident laser, which shows the same result as Figure 2. In region II (valley of the structure, where
![]() $0<x/\unicode[STIX]{x1D706}_{0}<1$
), the phase velocity (
$0<x/\unicode[STIX]{x1D706}_{0}<1$
), the phase velocity (
![]() $v_{p}=\unicode[STIX]{x1D714}/k=\text{d}x/\text{d}t$
) is getting larger, which means the valley is eventually filled by many electrons according to the dispersion relation
$v_{p}=\unicode[STIX]{x1D714}/k=\text{d}x/\text{d}t$
) is getting larger, which means the valley is eventually filled by many electrons according to the dispersion relation
![]() $\unicode[STIX]{x1D714}^{2}=\unicode[STIX]{x1D714}_{pe}^{2}+c^{2}k^{2}$
. In region III (inside the target, where
$\unicode[STIX]{x1D714}^{2}=\unicode[STIX]{x1D714}_{pe}^{2}+c^{2}k^{2}$
. In region III (inside the target, where
![]() $1<x/\unicode[STIX]{x1D706}_{0}<2$
), only weaker high-frequency components are observed, which means part of the transmitted radiation energy comes from the high-order harmonics generated on the target front surface. The high-order harmonics should be generated by the CSE mechanism because we can see an electron nanobunch[Reference Dromey, Cousens, Rykovanov, Yeung, Jung, Gautier, Dzelzainis, Kiefer, Palaniyppan, Shah, Schreiber, Fernandez, Lewis, Zepf and Hegelich25] in Figure 3(c). However, besides the CSE mechanism, the high-order harmonics could also be generated by the WTE[Reference Z.-Y., Cherednychek and Pukhov39] mechanism. Nevertheless, it is difficult to judge which the dominant radiation mechanism is, purely on the basis of this figure. The dominant radiation mechanism will be discussed further later in this paper. In region IV (vacuum behind the target, where
$1<x/\unicode[STIX]{x1D706}_{0}<2$
), only weaker high-frequency components are observed, which means part of the transmitted radiation energy comes from the high-order harmonics generated on the target front surface. The high-order harmonics should be generated by the CSE mechanism because we can see an electron nanobunch[Reference Dromey, Cousens, Rykovanov, Yeung, Jung, Gautier, Dzelzainis, Kiefer, Palaniyppan, Shah, Schreiber, Fernandez, Lewis, Zepf and Hegelich25] in Figure 3(c). However, besides the CSE mechanism, the high-order harmonics could also be generated by the WTE[Reference Z.-Y., Cherednychek and Pukhov39] mechanism. Nevertheless, it is difficult to judge which the dominant radiation mechanism is, purely on the basis of this figure. The dominant radiation mechanism will be discussed further later in this paper. In region IV (vacuum behind the target, where
![]() $x/\unicode[STIX]{x1D706}_{0}>2$
), the phase
$x/\unicode[STIX]{x1D706}_{0}>2$
), the phase
![]() $\unicode[STIX]{x1D711}=kx-\unicode[STIX]{x1D714}t$
of the transmitted radiation remains unchanged (see the black lines), and only the amplitude is reduced. It seems the target becomes transparent (or translucent) to the laser. However, region III shows that the laser does not really penetrate into the target, which means the transmitted radiation should be generated on the target back surface. Although Figure 3(b) shows results similar to Figure 3(a), there is a large difference in region IV. In Figure 3(a), each wavefront appears at
$\unicode[STIX]{x1D711}=kx-\unicode[STIX]{x1D714}t$
of the transmitted radiation remains unchanged (see the black lines), and only the amplitude is reduced. It seems the target becomes transparent (or translucent) to the laser. However, region III shows that the laser does not really penetrate into the target, which means the transmitted radiation should be generated on the target back surface. Although Figure 3(b) shows results similar to Figure 3(a), there is a large difference in region IV. In Figure 3(a), each wavefront appears at
![]() $x=2\unicode[STIX]{x1D706}_{0}$
. However, in Figure 3(b), the wavefront appears at
$x=2\unicode[STIX]{x1D706}_{0}$
. However, in Figure 3(b), the wavefront appears at
![]() $x=2.5\unicode[STIX]{x1D706}_{0}$
. Since Figures 3(a) and 3(b) have different
$x=2.5\unicode[STIX]{x1D706}_{0}$
. Since Figures 3(a) and 3(b) have different
![]() $y$
coordinates, we can conclude that the wavefront is discrete along the
$y$
coordinates, we can conclude that the wavefront is discrete along the
![]() $y$
axis for
$y$
axis for
![]() $2<x/\unicode[STIX]{x1D706}_{0}<2.5$
. The region
$2<x/\unicode[STIX]{x1D706}_{0}<2.5$
. The region
![]() $2<x/\unicode[STIX]{x1D706}_{0}<2.5$
is just the region where the transmitted radiation is generated. As a result, the discretely distributed wavefront implies the radiation source is also discretely distributed along the
$2<x/\unicode[STIX]{x1D706}_{0}<2.5$
is just the region where the transmitted radiation is generated. As a result, the discretely distributed wavefront implies the radiation source is also discretely distributed along the
![]() $y$
direction, which is shown in Figure 3(c). Figure 3(c) shows the electron density distribution on a logarithmic scale at
$y$
direction, which is shown in Figure 3(c). Figure 3(c) shows the electron density distribution on a logarithmic scale at
![]() $t=30T_{0}$
. On the back of the pre-structured target, we find some electron ‘islands’, with a minimum distance between two nearest islands of
$t=30T_{0}$
. On the back of the pre-structured target, we find some electron ‘islands’, with a minimum distance between two nearest islands of
![]() $\unicode[STIX]{x1D706}_{0}$
, which is also the distance between the two nearest elements of the newly generated wavefront. As a result, we can conclude that the transmitted radiation should be re-emitted by these electron ‘islands’. For the flat target, Figure 3(d) shows no obvious electron ‘islands’ on the target back surface, so we see weaker transmitted radiation in Figure 2(b).
$\unicode[STIX]{x1D706}_{0}$
, which is also the distance between the two nearest elements of the newly generated wavefront. As a result, we can conclude that the transmitted radiation should be re-emitted by these electron ‘islands’. For the flat target, Figure 3(d) shows no obvious electron ‘islands’ on the target back surface, so we see weaker transmitted radiation in Figure 2(b).

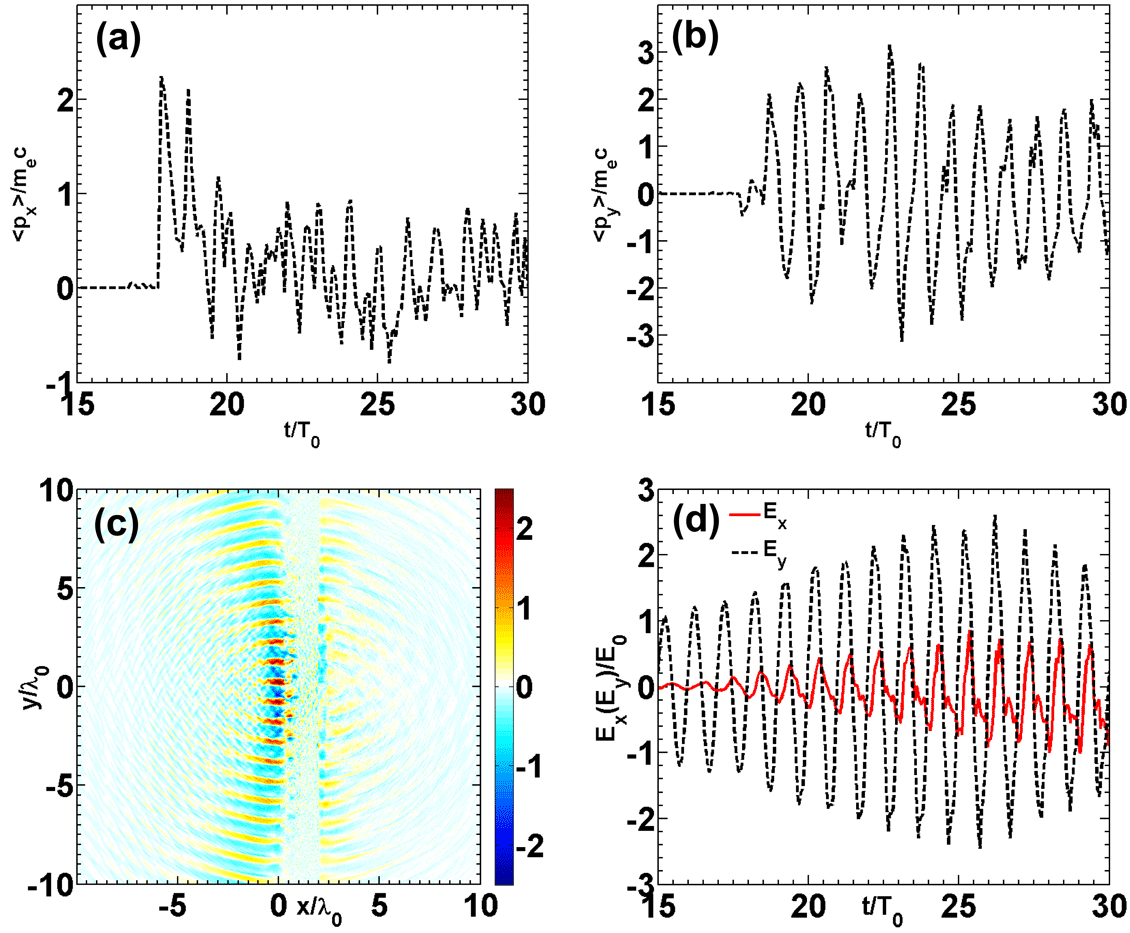
Figure 4. Time evolution of the averaged momentum of the electrons near the target back surface, snapshot of the SPW and time evolution of the electric fields at a point
![]() $(x_{1},y_{0})$
near the front surface. (a) is the evolution of
$(x_{1},y_{0})$
near the front surface. (a) is the evolution of
![]() $p_{x}$
, (b) is the evolution of
$p_{x}$
, (b) is the evolution of
![]() $p_{y}$
, (c) is the SPW
$p_{y}$
, (c) is the SPW
![]() $E_{x}/E_{0}$
(the electrostatic field
$E_{x}/E_{0}$
(the electrostatic field
![]() $\langle E_{x}/E_{0}\rangle$
, which is calculated by averaging
$\langle E_{x}/E_{0}\rangle$
, which is calculated by averaging
![]() $E_{x}/E_{0}$
in 5 laser cycles, is omitted) and (d) is the evolution of the electric fields
$E_{x}/E_{0}$
in 5 laser cycles, is omitted) and (d) is the evolution of the electric fields
![]() $E_{x}$
(red solid line) and
$E_{x}$
(red solid line) and
![]() $E_{y}$
(black dashed line). In (a) and (b), the momentum is calculated by
$E_{y}$
(black dashed line). In (a) and (b), the momentum is calculated by
![]() $\langle p_{\unicode[STIX]{x1D6FC}}\rangle =\sum p_{\unicode[STIX]{x1D6FC}i}/N$
(
$\langle p_{\unicode[STIX]{x1D6FC}}\rangle =\sum p_{\unicode[STIX]{x1D6FC}i}/N$
(
![]() $\unicode[STIX]{x1D6FC}=x,y$
), where
$\unicode[STIX]{x1D6FC}=x,y$
), where
![]() $p_{\unicode[STIX]{x1D6FC}i}$
is the
$p_{\unicode[STIX]{x1D6FC}i}$
is the
![]() $p_{\unicode[STIX]{x1D6FC}}$
of the
$p_{\unicode[STIX]{x1D6FC}}$
of the
![]() $i$
th electron in an area
$i$
th electron in an area
![]() $x\in (x_{0},x_{0}+\unicode[STIX]{x1D6FF}x)$
and
$x\in (x_{0},x_{0}+\unicode[STIX]{x1D6FF}x)$
and
![]() $y\in (y_{0},y_{0}+\unicode[STIX]{x1D6FF}y)$
, and
$y\in (y_{0},y_{0}+\unicode[STIX]{x1D6FF}y)$
, and
![]() $N$
is the total number.
$N$
is the total number.
As it is known from electrodynamics that the source of an electromagnetic field is the current, we need to further discuss the motion of the electron ‘islands’. For the transmitted
![]() $E_{y}$
, the source current is
$E_{y}$
, the source current is
![]() $j_{y}=-en_{e}p_{y}/\unicode[STIX]{x1D6FE}m_{e}$
, where the contribution of ion motion to the current is neglected. The wave equation is
$j_{y}=-en_{e}p_{y}/\unicode[STIX]{x1D6FE}m_{e}$
, where the contribution of ion motion to the current is neglected. The wave equation is
If we only consider the time evolution of
![]() $E_{y}$
at the point
$E_{y}$
at the point
![]() $(x_{0},y_{0})$
, the wave equation for the first wavefront (
$(x_{0},y_{0})$
, the wave equation for the first wavefront (
![]() $\unicode[STIX]{x1D6FB}^{2}E_{y}=0$
) becomes
$\unicode[STIX]{x1D6FB}^{2}E_{y}=0$
) becomes
However, even an area as small as an electron occupies cannot be called a geometrical point, so the current in Equation (2) should be replaced by
where
![]() $\unicode[STIX]{x0394}V=\unicode[STIX]{x1D6FF}x\unicode[STIX]{x1D6FF}y$
and
$\unicode[STIX]{x0394}V=\unicode[STIX]{x1D6FF}x\unicode[STIX]{x1D6FF}y$
and
![]() $\unicode[STIX]{x1D6FF}x,\unicode[STIX]{x1D6FF}y\ll \unicode[STIX]{x1D706}$
(the wavelength). As a result, we should consider
$\unicode[STIX]{x1D6FF}x,\unicode[STIX]{x1D6FF}y\ll \unicode[STIX]{x1D706}$
(the wavelength). As a result, we should consider
![]() $p_{y}$
as the momentum of the fluid elements, as well as the Lorentz factor
$p_{y}$
as the momentum of the fluid elements, as well as the Lorentz factor
![]() $\unicode[STIX]{x1D6FE}=\sqrt{1+(p_{x}/m_{e}c)^{2}+(p_{y}/m_{e}c)^{2}}$
. Figures 4(a) and 4(b) show the time evolution of the momentum of the fluid element in the area
$\unicode[STIX]{x1D6FE}=\sqrt{1+(p_{x}/m_{e}c)^{2}+(p_{y}/m_{e}c)^{2}}$
. Figures 4(a) and 4(b) show the time evolution of the momentum of the fluid element in the area
![]() $x\in (x_{0},x_{0}+\unicode[STIX]{x1D6FF}x)$
and
$x\in (x_{0},x_{0}+\unicode[STIX]{x1D6FF}x)$
and
![]() $y\in (y_{0},y_{0}+\unicode[STIX]{x1D6FF}y)$
near the target back surface. It is shown that the period of the
$y\in (y_{0},y_{0}+\unicode[STIX]{x1D6FF}y)$
near the target back surface. It is shown that the period of the
![]() $p_{x}$
is half the laser period and the peak amplitude is
$p_{x}$
is half the laser period and the peak amplitude is
![]() $p_{x}/m_{e}c\approx 2$
when the SPW is small (see
$p_{x}/m_{e}c\approx 2$
when the SPW is small (see
![]() $E_{x}$
in Figure 4(d)), but becomes
$E_{x}$
in Figure 4(d)), but becomes
![]() $p_{x}/m_{e}c\approx 0.8$
when the SPW grows larger. In Figure 4(b), the period of
$p_{x}/m_{e}c\approx 0.8$
when the SPW grows larger. In Figure 4(b), the period of
![]() $p_{y}$
is the laser period and the amplitude is
$p_{y}$
is the laser period and the amplitude is
![]() $p_{y}/m_{e}c\approx 2$
, which is nearly the same as the laser (see
$p_{y}/m_{e}c\approx 2$
, which is nearly the same as the laser (see
![]() $E_{y}$
in Figure 4(d)). The evolution is easily understood. With no driving laser on the target back surface, electron ‘islands’ should be formed by electrons from the target front. As a result, we firstly discuss the equations of motion of the electrons on the target front surface[Reference Lichters, ter Vehn and Pukhov10, Reference an der Brügge and Pukhov11, Reference Baeva, Gordienko and Pukhov40] together with the continuity equation and Poisson’s equation:
$E_{y}$
in Figure 4(d)). The evolution is easily understood. With no driving laser on the target back surface, electron ‘islands’ should be formed by electrons from the target front. As a result, we firstly discuss the equations of motion of the electrons on the target front surface[Reference Lichters, ter Vehn and Pukhov10, Reference an der Brügge and Pukhov11, Reference Baeva, Gordienko and Pukhov40] together with the continuity equation and Poisson’s equation:
where
![]() $\mathbf{A}$
is the vector potential,
$\mathbf{A}$
is the vector potential,
![]() $\unicode[STIX]{x1D719}$
is the electrostatic potential and
$\unicode[STIX]{x1D719}$
is the electrostatic potential and
![]() $E_{\text{SPW}}$
is the electric field intensity of the SPW. The electric field and the magnetic field of the laser are
$E_{\text{SPW}}$
is the electric field intensity of the SPW. The electric field and the magnetic field of the laser are
![]() $E_{y}=-\unicode[STIX]{x2202}_{t}A_{y}$
and
$E_{y}=-\unicode[STIX]{x2202}_{t}A_{y}$
and
![]() $B_{z}=-\unicode[STIX]{x2202}_{t}A_{y}/c$
, respectively. The electrostatic field is
$B_{z}=-\unicode[STIX]{x2202}_{t}A_{y}/c$
, respectively. The electrostatic field is
![]() $E_{x}=-\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D719}$
. In Equation (4), the contributions of the transverse electrostatic field and the SPW’s magnetic field are neglected because they are small variables compared to the laser field. For normal incidence
$E_{x}=-\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D719}$
. In Equation (4), the contributions of the transverse electrostatic field and the SPW’s magnetic field are neglected because they are small variables compared to the laser field. For normal incidence
![]() $\mathbf{p}_{0}=\mathbf{0}$
, we have
$\mathbf{p}_{0}=\mathbf{0}$
, we have
![]() $p_{y}/m_{e}c=eA_{y}/m_{e}c=a$
from Equation (4). For the first two cycles during the laser–plasma interaction, both the SPW and the electrostatic field are negligible because they are not excited (or very small) at this time, and we have
$p_{y}/m_{e}c=eA_{y}/m_{e}c=a$
from Equation (4). For the first two cycles during the laser–plasma interaction, both the SPW and the electrostatic field are negligible because they are not excited (or very small) at this time, and we have
![]() $p_{x}/m_{e}c=a^{2}/2=2$
from Equations (4) and (5). Afterwards, the ponderomotive force will be balanced by the electrostatic field, and we have
$p_{x}/m_{e}c=a^{2}/2=2$
from Equations (4) and (5). Afterwards, the ponderomotive force will be balanced by the electrostatic field, and we have
![]() $p_{x}=eE_{\text{SPW}}/m_{e}\unicode[STIX]{x1D714}_{0}c=a_{\text{SPW}}$
from Equation (5). With no (or small) collisional effects, the electrons will retain their momentum when they move inside the target before reaching the target back surface. As a result, the motion of the electrons on the target back surface is similar to that of the electrons on the front surface, as are shown in Figures 4(a) and 4(b). It is understandable that the positive amplitude of
$p_{x}=eE_{\text{SPW}}/m_{e}\unicode[STIX]{x1D714}_{0}c=a_{\text{SPW}}$
from Equation (5). With no (or small) collisional effects, the electrons will retain their momentum when they move inside the target before reaching the target back surface. As a result, the motion of the electrons on the target back surface is similar to that of the electrons on the front surface, as are shown in Figures 4(a) and 4(b). It is understandable that the positive amplitude of
![]() $p_{x}/m_{e}c$
is close to the negative amplitude of the SPW shown in Figure 4(d), because the negative part pushes the electrons inside the target. However, the SPW on the front surface cannot pull the electrons back to the target again. What pulls them back are the electrostatic fields and the SPW on the target back surface shown in Figure 4(c). The SPW on the target back surface is obviously weaker, so
$p_{x}/m_{e}c$
is close to the negative amplitude of the SPW shown in Figure 4(d), because the negative part pushes the electrons inside the target. However, the SPW on the front surface cannot pull the electrons back to the target again. What pulls them back are the electrostatic fields and the SPW on the target back surface shown in Figure 4(c). The SPW on the target back surface is obviously weaker, so
![]() $p_{x}/m_{e}c$
has a smaller negative amplitude. Once the electron ‘islands’ are formed, their densities are considered to be slow variables, so the frequencies of
$p_{x}/m_{e}c$
has a smaller negative amplitude. Once the electron ‘islands’ are formed, their densities are considered to be slow variables, so the frequencies of
![]() $j_{y}$
are controlled mainly by
$j_{y}$
are controlled mainly by
![]() $p_{y}/\unicode[STIX]{x1D6FE}$
. From the time evolution of
$p_{y}/\unicode[STIX]{x1D6FE}$
. From the time evolution of
![]() $p_{x}$
and
$p_{x}$
and
![]() $p_{y}$
, we know the fundamental frequency of
$p_{y}$
, we know the fundamental frequency of
![]() $j_{y}$
is the laser frequency; which is why the fundamental frequency of the transmitted radiation is also the laser frequency, as is shown in Figure 2(d). For the flat target where no SPW is excited, without the help of the SPW, few electrons reach the target back surface after the ponderomotive force is balanced by the electrostatic field and no electron ‘islands’ are formed on the target back surface, as is shown in Figure 3(d). As a result, no transmitted radiation with the fundamental frequency is generated. Since the transmitted radiation is actually generated by these electron ‘islands’, one way of increasing the intensity of the transmitted radiation is by increasing the density of the ‘islands’. Three-dimensional (3D) PIC simulations are also performed to prove the validity of our mechanism. In 3D PIC simulations, we also observe the transmitted radiation – the most important difference from the 2D PIC simulations being that the percentage of the transmitted energy is slightly decreased; it is only about 1.5% in the 3D case. We also investigate the influence of the pre-plasma on our mechanism, and the initial plasma density is shown in Figure 5(a). In Figure 5(a), the valleys of the target structure are filled by a plasma with an electron density
$j_{y}$
is the laser frequency; which is why the fundamental frequency of the transmitted radiation is also the laser frequency, as is shown in Figure 2(d). For the flat target where no SPW is excited, without the help of the SPW, few electrons reach the target back surface after the ponderomotive force is balanced by the electrostatic field and no electron ‘islands’ are formed on the target back surface, as is shown in Figure 3(d). As a result, no transmitted radiation with the fundamental frequency is generated. Since the transmitted radiation is actually generated by these electron ‘islands’, one way of increasing the intensity of the transmitted radiation is by increasing the density of the ‘islands’. Three-dimensional (3D) PIC simulations are also performed to prove the validity of our mechanism. In 3D PIC simulations, we also observe the transmitted radiation – the most important difference from the 2D PIC simulations being that the percentage of the transmitted energy is slightly decreased; it is only about 1.5% in the 3D case. We also investigate the influence of the pre-plasma on our mechanism, and the initial plasma density is shown in Figure 5(a). In Figure 5(a), the valleys of the target structure are filled by a plasma with an electron density
![]() $n_{e}=2n_{c}$
. Also, the electron density between
$n_{e}=2n_{c}$
. Also, the electron density between
![]() $x/\unicode[STIX]{x1D706}_{0}=-2$
and
$x/\unicode[STIX]{x1D706}_{0}=-2$
and
![]() $x=0$
increases exponentially from zero to
$x=0$
increases exponentially from zero to
![]() $2n_{c}$
. The electron density of the pre-structured target is
$2n_{c}$
. The electron density of the pre-structured target is
![]() $n_{e}=25n_{c}$
. More detailed information is shown in the inserted figure in Figure 5(a). The case without a pre-plasma is also simulated for comparison. In both cases, the laser normalized vector potential is
$n_{e}=25n_{c}$
. More detailed information is shown in the inserted figure in Figure 5(a). The case without a pre-plasma is also simulated for comparison. In both cases, the laser normalized vector potential is
![]() $a_{0}=3$
. Figures 5(b) and 5(c) show the electric fields
$a_{0}=3$
. Figures 5(b) and 5(c) show the electric fields
![]() $E_{y}$
on the
$E_{y}$
on the
![]() $x$
axis and their spectra for both cases at
$x$
axis and their spectra for both cases at
![]() $t=25T_{0}$
. It is obvious from Figure 5(b) that, with a pre-plasma on the target front surface, the intensity of the transmitted radiation is decreased. This happens mainly because the laser wavelength in the pre-plasma is no longer
$t=25T_{0}$
. It is obvious from Figure 5(b) that, with a pre-plasma on the target front surface, the intensity of the transmitted radiation is decreased. This happens mainly because the laser wavelength in the pre-plasma is no longer
![]() $\unicode[STIX]{x1D706}_{0}$
and the matching condition of the SPW excitation is no longer met. As a result, the SPW will be decreased, as is shown in Figure 5(d), which shows a snapshot of the electric field
$\unicode[STIX]{x1D706}_{0}$
and the matching condition of the SPW excitation is no longer met. As a result, the SPW will be decreased, as is shown in Figure 5(d), which shows a snapshot of the electric field
![]() $E_{x}$
for the case with a pre-plasma at
$E_{x}$
for the case with a pre-plasma at
![]() $t=25T_{0}$
. From Figure 5 we can see that the intensity of the SPW is greatly decreased compared to that shown in Figure 4(c). When the intensity of the SPW is decreased, the number of the electrons that penetrate through the target is also decreased, which results in a lower intensity of the transmitted radiation. From the spectra shown in Figure 5(c), we also find that the high-order harmonic generation will also be suppressed by the pre-plasma. However, it is shown in Ref. [Reference Z.-Y., Cherednychek and Pukhov39] that the pre-plasma will help the WTE to occur, so we can conclude from Figure 5(c) that the high-order harmonic generation inside the target is not dominated by the WTE. To avoid the influence of the pre-plasma generated by the pre-pulse of the laser, the drive laser should have a sufficiently high contrast.
$t=25T_{0}$
. From Figure 5 we can see that the intensity of the SPW is greatly decreased compared to that shown in Figure 4(c). When the intensity of the SPW is decreased, the number of the electrons that penetrate through the target is also decreased, which results in a lower intensity of the transmitted radiation. From the spectra shown in Figure 5(c), we also find that the high-order harmonic generation will also be suppressed by the pre-plasma. However, it is shown in Ref. [Reference Z.-Y., Cherednychek and Pukhov39] that the pre-plasma will help the WTE to occur, so we can conclude from Figure 5(c) that the high-order harmonic generation inside the target is not dominated by the WTE. To avoid the influence of the pre-plasma generated by the pre-pulse of the laser, the drive laser should have a sufficiently high contrast.
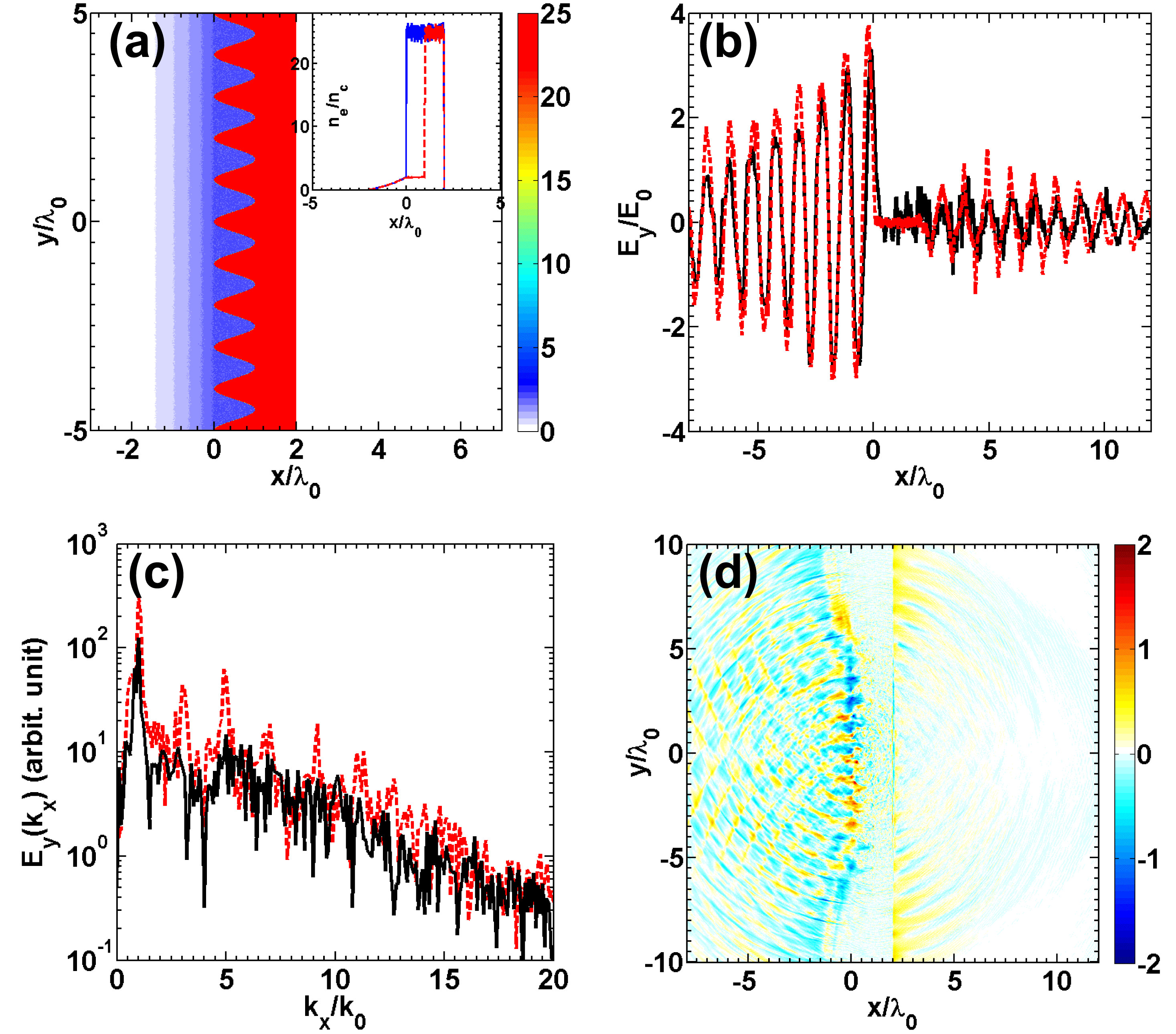
Figure 5. Comparison between the cases with and without a pre-plasma. (a) is the initial electron density with a pre-plasma, (b) is the electric field
![]() $E_{y}$
on the
$E_{y}$
on the
![]() $x$
axis for cases with a pre-plasma (black solid line) and without a pre-plasma (red dashed line), (c) is the spectra of the electric fields shown in (b) (the black solid line also represents the case with a pre-plasma) and (d) is a snapshot of the electric field
$x$
axis for cases with a pre-plasma (black solid line) and without a pre-plasma (red dashed line), (c) is the spectra of the electric fields shown in (b) (the black solid line also represents the case with a pre-plasma) and (d) is a snapshot of the electric field
![]() $E_{x}$
, with
$E_{x}$
, with
![]() $\langle E_{x}/E_{0}\rangle$
omitted. In the inserted figure of (a), the electron density distribution along the
$\langle E_{x}/E_{0}\rangle$
omitted. In the inserted figure of (a), the electron density distribution along the
![]() $x$
axis is shown on
$x$
axis is shown on
![]() $y=0$
(blue line) and on
$y=0$
(blue line) and on
![]() $y=\unicode[STIX]{x1D706}_{0}/2$
(red line).
$y=\unicode[STIX]{x1D706}_{0}/2$
(red line).
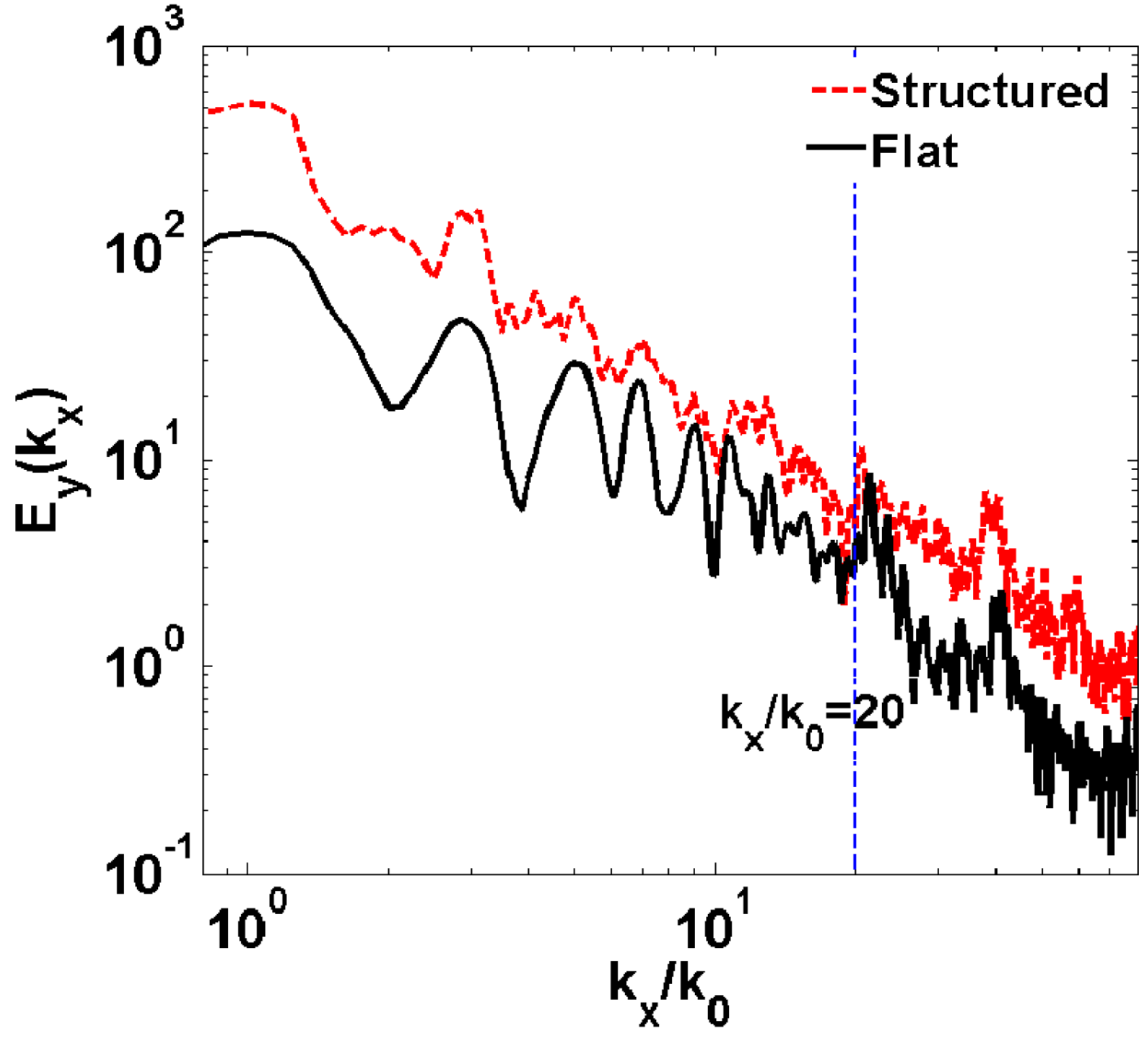
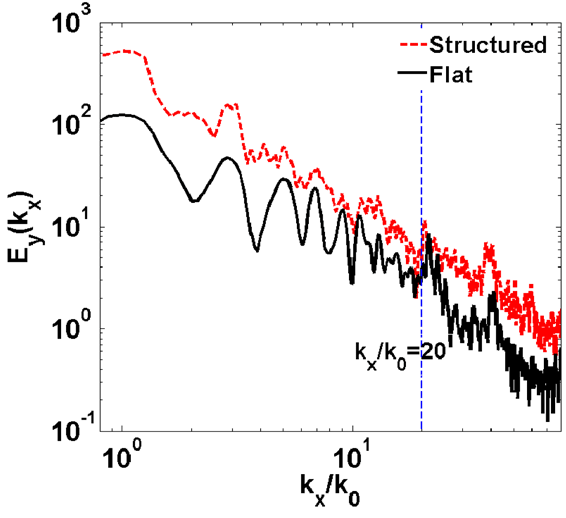
Figure 6. Spectra of the transmitted radiation behind the pre-structured target (red dashed line) and the flat target (black solid line). In this case
![]() $a_{0}=12$
and
$a_{0}=12$
and
![]() $n_{e}=400n_{c}$
.
$n_{e}=400n_{c}$
.
To investigate the enhancement of the higher-order harmonics, we continue to increase the laser normalized vector potential to
![]() $a_{0}=12$
. The electron density is
$a_{0}=12$
. The electron density is
![]() $n_{e}=400n_{c}$
, while the other simulation parameters are the same as in the above simulations. The spectra of the transmitted radiation behind the flat target and the pre-structured target are plotted in Figure 6. It is shown that the spectra of radiation behind both the pre-structured target and the flat target experience a jump at
$n_{e}=400n_{c}$
, while the other simulation parameters are the same as in the above simulations. The spectra of the transmitted radiation behind the flat target and the pre-structured target are plotted in Figure 6. It is shown that the spectra of radiation behind both the pre-structured target and the flat target experience a jump at
![]() $k/k_{0}=20$
. This happens because the harmonics with orders higher than 20 contain radiation generated both in front of and behind the target; however, lower-order harmonics generated in front of the target will be filtered by the solid target. It is also shown that the intensity of the higher-order harmonics behind the pre-structured target is much enhanced compared to that behind the flat target. The higher-order harmonics are also enhanced by the SPW, because the SPW helps drag more electrons out of the target surface and also helps heat the dragged-out electrons to a higher energy.
$k/k_{0}=20$
. This happens because the harmonics with orders higher than 20 contain radiation generated both in front of and behind the target; however, lower-order harmonics generated in front of the target will be filtered by the solid target. It is also shown that the intensity of the higher-order harmonics behind the pre-structured target is much enhanced compared to that behind the flat target. The higher-order harmonics are also enhanced by the SPW, because the SPW helps drag more electrons out of the target surface and also helps heat the dragged-out electrons to a higher energy.
Simulations with different target thicknesses were also performed, but the results are not shown in the paper. The simulation results show that as the target becomes thicker, the intensity of the transmitted laser decreases, and may even disappear. What restricts the target thickness is the so-called ‘return current’. When an electron bunch propagates in a plasma, the background cold electrons can go back to generate a so-called ‘return current’. The return current will generate magnetic fields that can change the propagation direction of the electron bunch. When the target is thick enough, the propagation directions of these electrons with lower energy can even change by more than
![]() $90^{\circ }$
. As a result, fewer electrons reach the target back surface to generate transmitted radiation.
$90^{\circ }$
. As a result, fewer electrons reach the target back surface to generate transmitted radiation.
3 Conclusion
In conclusion, we investigate the interaction between an intense laser and an overdense plasma slab with the help of 2D and 3D PIC simulations. It is shown that, even if the plasma density is far higher than the relativistically critical density and the thickness is also much greater than the skin depth, considerable laser energy penetrates the plasma slab when the target is pre-structured. Compared to the flat target, the transmitted laser energy behind the pre-structured is increased by about two orders of magnitude. Detailed analyses show that the ‘transmitted’ radiation behind the pre-structured target is actually radiated by the electron ‘islands’ on the target back surface. Also these electron ‘islands’ are generated by the SPW excited on the target front surface. When the SPW is excited on the target front surface, more hot electrons with higher energies will be generated, and some of these hot electrons will get to the target rear surface to generate electron bunches with the help of the SPW. It is also shown that the transmitted radiation contains high-order harmonics, the intensity of which behind the pre-structured target is also greatly enhanced compared to behind the flat target. The enhancement of the higher-order harmonics is also related to the excitation of the SPWs, because the SPWs will increase both the number and energy of the electrons that radiate the high-order harmonics. It is also shown that the pre-plasma will have a negative influence on the SPW excitation; as a result, the intensity of the transmitted radiation will be decreased when the SPW generation is suppressed by the pre-plasma. To avoid or weaken the influence of the pre-plasma, a laser with higher contrast is needed.
Acknowledgements
This research was supported by the Science Challenge Project (No. TZ2016005), China Postdoctoral Science Foundation (No. 2017M620430), National Natural Science Foundation of China (Nos. 11435011, 11575035, 11705180, and 11875241) and the National Basic Research Program of China (No. 2013CB834101).