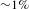1 Introduction
Free-electron lasers (FELs), which serve as tunable coherent sources of short-wavelength radiation, have attracted considerable attention owing to their widespread application in spectroscopy[Reference Takahashi, Brunel, Edwards, Tol, Ramian, Han and Sherwin1], materials science[Reference Young, Kanter, Krässig, Li, March, Pratt, Santra, Southworth, Rohringer, Dimauro, Doumy, Roedig, Berrah, Fang, Hoener, Bucksbaum, Cryan, Ghimire, Glownia, Reis, Bozek, Bostedt and Messerschmidt2], biology[Reference Barends, Foucar, Botha, Doak, Shoeman, Nass, Koglin, Williams, Boutet, Messerschmidt and Schlichting3] and other fields[Reference Bilderback, Elleaume and Weckert4, Reference Tono5]. Several FEL facilities based on state-of-the-art linear accelerators have been operated successfully at X-ray wavelengths[Reference Ackermann, Asova, Ayvazyan, Azima, Baboi, Bahr, Balandin, Beutner, Brandt, Bolzmann, Brinkmann, Brovko, Castellano, Castro, Catani, Chiadroni, Choroba, Cianchi, Costello, Cubaynes, Dardis, Decking, Delsim-Hashemi, Delserieys, Pirro, Dohlus, Dusterer, Eckhardt, Edwards, Faatz, Feldhaus, Flottmann, Frisch, Fröhlich, Garvey, Gensch, Gerth, Gorler, Golubeva, Grabosch, Grecki, Grimm, Hacker, Hahn, Han, Honkavaara, Hott, Hüning, Ivanisenko, Jaeschke, Jalmuzna, Jezynski, Kammering, Katalev, Kavanagh, Kennedy, Khodyachykh, Klose, Kocharyan, Korfer, Kollewe, Koprek, Korepanov, Kostin, Krassilnikov, Kube, Kuhlmann, Lewis, Lilje, Limberg, Lipka, Löhl, Luna, Luong, Martins, Meyer, Michelato, Miltchev, Moller, Monaco, Muller, Napieralski, Napoly, Nicolosi, Nolle, Nunez, Oppelt, Pagani, Paparella, Pchalek, Pedregosa-Gutierrez, Petersen, Petrosyan, Petrosyan, Petrosyan, Pfluger, Plonjes, Poletto, Pozniak, Prat, Proch, Pucyk, Radcliffe, Redlin, Rehlich, Richter, Roehrs, Roensch, Romaniuk, Ross, Rossbach, Rybnikov, Sachwitz, Saldin, Sandner, Schlarb, Schmidt, Schmitz, Schmuser, Schneider, Schneidmiller, Schnepp, Schreiber, Seidel, Sertore, Shabunov, Simon, Simrock, Sombrowski, Sorokin, Spanknebel, Spesyvtsev, Staykov, Steffen, Stephan, Stulle, Thom, Tiedtke, Tischer, Toleikis, Treusch, Trines, Tsakov, Vogel, Weiland, Weise, Wellhofer, Wendt, Will, Winter, Wittenburg, Wurth, Yeates, Yurkov, Zagorodnov and Zapfe6–Reference Ishikawa, Aoyagi, Asaka, Asano, Azumi, Bizen, Ego, Fukami, Fukui, Furukawa, Goto, Hanaki, Hara, Hasegawa, Hatsui, Higashiya, Hirono, Hosoda, Ishii, Inagaki, Inubushi, Itoga, Joti, Kago, Kameshima, Kimura, Kirihara, Kiyomichi, Kobayashi, Kondo, Kudo, Maesaka, Mar’echal, Masuda, Matsubara, Matsumoto, Matsushita, Matsui, Nagasono, Nariyama, Ohashi, Ohata, Ohshima, Ono, Otake, Saji, Sakurai, Sato, Sawada, Seike, Shirasawa, Sugimoto, Suzuki, Takahashi, Takebe, Takeshita, Tamasaku, Tanaka, Tanaka, Tanaka, Togashi, Togawa, Tokuhisa, Tomizawa, Tono, Wu, Yabashi, Yamaga, Yamashita, Yanagida, Zhang, Shintake, Kitamura and Kumagai9] but have hitherto been limited to these large facilities, which are costly and only accessible to limited users. It is highly desirable to develop a compact and affordable laboratory-scale electron accelerator. In recent years, remarkable progress has been made in generating high-energy (
![]() ${\sim}1$
GeV), high-peak current (
${\sim}1$
GeV), high-peak current (
![]() ${\sim}10$
kA), and low-emittance (
${\sim}10$
kA), and low-emittance (
![]() ${\sim}0.1~\unicode[STIX]{x03BC}\text{m}$
) electron beams (
${\sim}0.1~\unicode[STIX]{x03BC}\text{m}$
) electron beams (
![]() $e$
beams) using laser wakefield accelerators (LWFAs) [Reference Tajima and Dawson10–Reference Hafz, Li, Li, Mohammad, Zeng and Zhang18]. Such accelerators can be used for driving next-generation advanced light sources. However, these
$e$
beams) using laser wakefield accelerators (LWFAs) [Reference Tajima and Dawson10–Reference Hafz, Li, Li, Mohammad, Zeng and Zhang18]. Such accelerators can be used for driving next-generation advanced light sources. However, these
![]() $e$
beams usually have a large energy spread of a few percent[Reference Rechatin, Faure, Benismail, Lim, Fitour, Specka, Videau, Tafzi, Burgy and Malka19, Reference Mirzaie, Li, Zeng, Hafz, Chen, Li, Zhu, Liao, Sokollik, Liu, Ma, Chen, Sheng and Zhang20], which degrades the FEL gain[Reference Huang and Kim21]. Various efforts have been directed toward energy-spread compression in LWFAs via energy chirp control[Reference Wang, Li, Liu, Zhang, Qi, Yu, Liu, Fang, Qin, Wang, Xu, Wu, Leng, Li and Xu17, Reference Zhang, Liu, Wang, Li, Yu, Tian, Qi, Wang, Qin, Fang, Liu, Nakajima, Li and Xu22]. Researchers have also focused on compensating the large energy-spread effects in high-gain FELs by using a transverse gradient undulator (TGU) together with a properly dispersed
$e$
beams usually have a large energy spread of a few percent[Reference Rechatin, Faure, Benismail, Lim, Fitour, Specka, Videau, Tafzi, Burgy and Malka19, Reference Mirzaie, Li, Zeng, Hafz, Chen, Li, Zhu, Liao, Sokollik, Liu, Ma, Chen, Sheng and Zhang20], which degrades the FEL gain[Reference Huang and Kim21]. Various efforts have been directed toward energy-spread compression in LWFAs via energy chirp control[Reference Wang, Li, Liu, Zhang, Qi, Yu, Liu, Fang, Qin, Wang, Xu, Wu, Leng, Li and Xu17, Reference Zhang, Liu, Wang, Li, Yu, Tian, Qi, Wang, Qin, Fang, Liu, Nakajima, Li and Xu22]. Researchers have also focused on compensating the large energy-spread effects in high-gain FELs by using a transverse gradient undulator (TGU) together with a properly dispersed
![]() $e$
beam[Reference Smith, Madey, Elias and Deacon23–Reference Baxevanis, Ding, Huang and Ruth25]. The dispersion of the
$e$
beam[Reference Smith, Madey, Elias and Deacon23–Reference Baxevanis, Ding, Huang and Ruth25]. The dispersion of the
![]() $e$
beam must be matched with the transverse gradient field of the TGU to satisfy the resonant condition[Reference Huang, Ding and Schroeder24]. However, the transversely tapered TGUs require a special design and manufacturing process, and the transverse gradient cannot be tuned arbitrarily. A similar scheme using the natural transverse gradient of a normal planar undulator (PU) doubling as a TGU was recently proposed[Reference Jia and Li26], where the vertical dispersion of the
$e$
beam must be matched with the transverse gradient field of the TGU to satisfy the resonant condition[Reference Huang, Ding and Schroeder24]. However, the transversely tapered TGUs require a special design and manufacturing process, and the transverse gradient cannot be tuned arbitrarily. A similar scheme using the natural transverse gradient of a normal planar undulator (PU) doubling as a TGU was recently proposed[Reference Jia and Li26], where the vertical dispersion of the
![]() $e$
beam is introduced.
$e$
beam is introduced.
In this study, we investigate a simple scheme to improve the performance of the radiation using a PU together with a properly dispersed
![]() $e$
beam from the LWFA. Our scheme has no need of extra field for correcting the orbit deflection induced by the field gradient and is easy to implement. In the proposed scheme, the energy of the
$e$
beam from the LWFA. Our scheme has no need of extra field for correcting the orbit deflection induced by the field gradient and is easy to implement. In the proposed scheme, the energy of the
![]() $e$
beam is dispersed with its horizontal position so that only the center electrons satisfy the resonant condition, but the frequency detuning increases when the electrons deviate from the beam center, which inhibits the radiation growth. This mechanism can be regarded as a selection process, in which the PU acts as a filter for selecting the electrons near the beam center to achieve the radiation. Although only the center electrons contribute, the radiation can be enhanced owing to the high-peak current of the
$e$
beam is dispersed with its horizontal position so that only the center electrons satisfy the resonant condition, but the frequency detuning increases when the electrons deviate from the beam center, which inhibits the radiation growth. This mechanism can be regarded as a selection process, in which the PU acts as a filter for selecting the electrons near the beam center to achieve the radiation. Although only the center electrons contribute, the radiation can be enhanced owing to the high-peak current of the
![]() $e$
beam. Theoretical analysis and numerical simulations demonstrate the feasibility of a self-amplified spontaneous emission (SASE) FEL with sub-gigawatt power, a narrow bandwidth (
$e$
beam. Theoretical analysis and numerical simulations demonstrate the feasibility of a self-amplified spontaneous emission (SASE) FEL with sub-gigawatt power, a narrow bandwidth (
![]() ${<}1\%$
) and good transverse coherence in the proposed scheme with typical parameters of the
${<}1\%$
) and good transverse coherence in the proposed scheme with typical parameters of the
![]() $e$
beam from the LWFA.
$e$
beam from the LWFA.

Figure 1. SASE FEL scheme using the PU with the
![]() $e$
beam from the LWFA. The transverse distribution of the
$e$
beam from the LWFA. The transverse distribution of the
![]() $e$
beam (a) without and (c) with the transverse dispersion. (b), (d) Corresponding angular profiles of the radiation power.
$e$
beam (a) without and (c) with the transverse dispersion. (b), (d) Corresponding angular profiles of the radiation power.
2 Dispersion effects on FEL radiation
Assuming a highly relativistic
![]() $e$
beam with normalized energy
$e$
beam with normalized energy
![]() $\unicode[STIX]{x1D6FE}_{0}$
propagating through an undulator with the period
$\unicode[STIX]{x1D6FE}_{0}$
propagating through an undulator with the period
![]() $\unicode[STIX]{x1D706}_{u}$
and strength parameter
$\unicode[STIX]{x1D706}_{u}$
and strength parameter
![]() $K_{0}$
, the on-axis radiation wavelength is
$K_{0}$
, the on-axis radiation wavelength is
![]() $\unicode[STIX]{x1D706}_{r}=\unicode[STIX]{x1D706}_{u}(1+K_{0}^{2}/2)/2\unicode[STIX]{x1D6FE}_{0}^{2}$
. To obtain a high-gain FEL, the beam energy spread
$\unicode[STIX]{x1D706}_{r}=\unicode[STIX]{x1D706}_{u}(1+K_{0}^{2}/2)/2\unicode[STIX]{x1D6FE}_{0}^{2}$
. To obtain a high-gain FEL, the beam energy spread
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FF}}$
should satisfy[Reference Huang and Kim21]
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FF}}$
should satisfy[Reference Huang and Kim21]
to prevent the velocity difference from washing out the micro-bunching buildup. Here,
![]() $\unicode[STIX]{x1D70C}$
is the dimensionless Pierce parameter, which can be defined as[Reference Huang and Kim21, Reference Bonifacio, Pellegrini and Narducci27]
$\unicode[STIX]{x1D70C}$
is the dimensionless Pierce parameter, which can be defined as[Reference Huang and Kim21, Reference Bonifacio, Pellegrini and Narducci27]
where
![]() $I_{p}$
is the peak current,
$I_{p}$
is the peak current,
![]() $I_{A}$
is the Alfvén current,
$I_{A}$
is the Alfvén current,
![]() $\unicode[STIX]{x1D70E}_{x}$
is the root-mean-square (RMS) transverse beam size,
$\unicode[STIX]{x1D70E}_{x}$
is the root-mean-square (RMS) transverse beam size,
![]() $k_{u}=2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D706}_{u}$
, and
$k_{u}=2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D706}_{u}$
, and
![]() $[JJ]=[J_{0}(\unicode[STIX]{x1D709})-J_{1}(\unicode[STIX]{x1D709})]$
, with
$[JJ]=[J_{0}(\unicode[STIX]{x1D709})-J_{1}(\unicode[STIX]{x1D709})]$
, with
![]() $\unicode[STIX]{x1D709}=K_{0}^{2}/(4+2K_{0}^{2})$
. However, satisfying Equation (1) remains a challenge for
$\unicode[STIX]{x1D709}=K_{0}^{2}/(4+2K_{0}^{2})$
. However, satisfying Equation (1) remains a challenge for
![]() $e$
beams from LWFAs.
$e$
beams from LWFAs.
Considering an
![]() $e$
beam with horizontal dispersion
$e$
beam with horizontal dispersion
![]() $D_{x}$
, the horizontal position of the electrons depends on the energy:
$D_{x}$
, the horizontal position of the electrons depends on the energy:
![]() $x=D_{x}\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FE}_{0}$
, as shown in Figure 1(c). The wavelength of the radiation emitted by the off-center electrons deviates from the center wavelength according to the resonant condition of the undulator. The corresponding angular profiles of the radiation power obtained by
$x=D_{x}\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FE}_{0}$
, as shown in Figure 1(c). The wavelength of the radiation emitted by the off-center electrons deviates from the center wavelength according to the resonant condition of the undulator. The corresponding angular profiles of the radiation power obtained by
![]() $e$
beams without and with the dispersion are shown in Figures 1(b) and 1(d), respectively.
$e$
beams without and with the dispersion are shown in Figures 1(b) and 1(d), respectively.
Once the horizontal dispersion is introduced, the horizontal size of the
![]() $e$
beam increases to
$e$
beam increases to
![]() $\unicode[STIX]{x1D70E}_{T}=(\unicode[STIX]{x1D70E}_{x}^{2}+D_{x}^{2}\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FF}}^{2})^{1/2}$
, and the density of the
$\unicode[STIX]{x1D70E}_{T}=(\unicode[STIX]{x1D70E}_{x}^{2}+D_{x}^{2}\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FF}}^{2})^{1/2}$
, and the density of the
![]() $e$
beam decreases. Using the method of perturbation analysis and integration along the unperturbed trajectories[Reference Baxevanis, Ding, Huang and Ruth25], the effective energy spread can be reduced as follows:
$e$
beam decreases. Using the method of perturbation analysis and integration along the unperturbed trajectories[Reference Baxevanis, Ding, Huang and Ruth25], the effective energy spread can be reduced as follows:
and the attenuated FEL parameter is given as
As indicated by Equation (3),
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FF}}^{ef}$
depends on the properties of the
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FF}}^{ef}$
depends on the properties of the
![]() $e$
beam and not the type of undulator. A significantly reduced effective energy spread is required for optimum operation of the FEL; thus, we can usually approximate
$e$
beam and not the type of undulator. A significantly reduced effective energy spread is required for optimum operation of the FEL; thus, we can usually approximate
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FF}}^{ef}\approx \unicode[STIX]{x1D70E}_{x}/D_{x}$
.
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FF}}^{ef}\approx \unicode[STIX]{x1D70E}_{x}/D_{x}$
.

Figure 2. (a) Radiation power along the PU around 30 nm; (b) single-shot spectra of an SASE FEL; (c), (d) corresponding transverse angular profiles of the radiation power obtained by
![]() $e$
beam without and with the horizontal dispersion.
$e$
beam without and with the horizontal dispersion.
We attempt to perform the EUV FEL operation by employing the attainable LWFA beam parameters from Shanghai Institute of Optics and Fine Mechanics (SIOM)[Reference Wang, Li, Liu, Zhang, Qi, Yu, Liu, Fang, Qin, Wang, Xu, Wu, Leng, Li and Xu17, Reference Qin, Yu, Wang, Liu, Li, Qi, Zhang, Liu, Fang, Feng, Wu, Ke, Chen, Xu, Leng, Wang, Li and Xu28, Reference Fang, Wang, Zhang, Liu, Yu, Qi, Qin, Liu, Feng, Wu, Wang, Liu, Wang, Xu, Wu, Leng, Li and Xu29] and the compact beam transport system considered in Ref. [Reference Liu, Zhang, Wang and Huang30]. The parameters for the
![]() $e$
beam at the entrance of the undulator are shown in Table 1. For a short undulator of length
$e$
beam at the entrance of the undulator are shown in Table 1. For a short undulator of length
![]() $L_{u}$
without external focusing, it is reasonable to assume a beta function of
$L_{u}$
without external focusing, it is reasonable to assume a beta function of
![]() $\unicode[STIX]{x1D6FD}=L_{u}/2=3~\text{m}$
. Thus, the initial transverse beam size is estimated as
$\unicode[STIX]{x1D6FD}=L_{u}/2=3~\text{m}$
. Thus, the initial transverse beam size is estimated as
![]() $\unicode[STIX]{x1D70E}_{x}=\unicode[STIX]{x1D70E}_{y}=20~\unicode[STIX]{x03BC}\text{m}$
. The horizontal dispersion is chosen as
$\unicode[STIX]{x1D70E}_{x}=\unicode[STIX]{x1D70E}_{y}=20~\unicode[STIX]{x03BC}\text{m}$
. The horizontal dispersion is chosen as
![]() $D_{x}=2.5$
cm, which is the optimum dispersion of the beam according to the simulation results presented in the next section. Here, only the linear dispersion is considered in our simulation. It is noted that the beta function is the one before introducing the dispersion[Reference Huang, Ding and Schroeder24, Reference Jia and Li26]. As we discuss in the following part, only the electrons near the beam center achieve the radiation. The beta function for the central electrons in the beam remains the same as the beta function for the whole beam after removing the influence of the dispersion. After the dispersion is introduced, the horizontal beam size increases to
$D_{x}=2.5$
cm, which is the optimum dispersion of the beam according to the simulation results presented in the next section. Here, only the linear dispersion is considered in our simulation. It is noted that the beta function is the one before introducing the dispersion[Reference Huang, Ding and Schroeder24, Reference Jia and Li26]. As we discuss in the following part, only the electrons near the beam center achieve the radiation. The beta function for the central electrons in the beam remains the same as the beta function for the whole beam after removing the influence of the dispersion. After the dispersion is introduced, the horizontal beam size increases to
![]() $\unicode[STIX]{x1D70E}_{T}=250~\unicode[STIX]{x03BC}\text{m}$
.
$\unicode[STIX]{x1D70E}_{T}=250~\unicode[STIX]{x03BC}\text{m}$
.
Table 1.
![]() $E$
beam and undulator parameters used in our study for EUV and soft X-ray FELs.
$E$
beam and undulator parameters used in our study for EUV and soft X-ray FELs.

The FEL radiation was simulated in the time-dependent mode of GENESIS, which includes three-dimensional (3D) effects, such as the diffraction and transverse modes[Reference Reiche31]. Figure 2(a) shows the FEL power along the PU for SASE using
![]() $e$
beams with (blue) and without (black) the horizontal dispersion. For a 6 m undulator, the radiation power increases by almost three orders of magnitude when the horizontal dispersion of the
$e$
beams with (blue) and without (black) the horizontal dispersion. For a 6 m undulator, the radiation power increases by almost three orders of magnitude when the horizontal dispersion of the
![]() $e$
beam is introduced. Figure 2(b) shows the typical single-shot spectra for the two different cases. A single coherent spike is generated with an RMS bandwidth of 1% by using the dispersed
$e$
beam is introduced. Figure 2(b) shows the typical single-shot spectra for the two different cases. A single coherent spike is generated with an RMS bandwidth of 1% by using the dispersed
![]() $e$
beam. Figures 2(c) and 2(d) show the corresponding angular patterns of the FEL radiation. Without the initial
$e$
beam. Figures 2(c) and 2(d) show the corresponding angular patterns of the FEL radiation. Without the initial
![]() $e$
-beam dispersion, the divergence angle is large owing to the large emittance of the
$e$
-beam dispersion, the divergence angle is large owing to the large emittance of the
![]() $e$
beam and the relatively low gain, as shown in Figure 2(c). The angular property is significantly improved with a dispersed
$e$
beam and the relatively low gain, as shown in Figure 2(c). The angular property is significantly improved with a dispersed
![]() $e$
beam, as shown in Figure 2(d).
$e$
beam, as shown in Figure 2(d).
We now consider an FEL operating at the ‘water window’ radiation wavelength. The parameters of the
![]() $e$
beam and the undulator considered in Ref. [Reference Huang, Ding and Schroeder24] are used. The transverse dispersion is
$e$
beam and the undulator considered in Ref. [Reference Huang, Ding and Schroeder24] are used. The transverse dispersion is
![]() $D_{x}=2$
cm. Reasonably assuming a beta function of
$D_{x}=2$
cm. Reasonably assuming a beta function of
![]() $\unicode[STIX]{x1D6FD}=L_{u}/2=3$
m, we obtain an initial beam size of
$\unicode[STIX]{x1D6FD}=L_{u}/2=3$
m, we obtain an initial beam size of
![]() $\unicode[STIX]{x1D70E}_{x}=\unicode[STIX]{x1D70E}_{y}=12.4~\unicode[STIX]{x03BC}\text{m}$
. After dispersion, the horizontal beam size increases to
$\unicode[STIX]{x1D70E}_{x}=\unicode[STIX]{x1D70E}_{y}=12.4~\unicode[STIX]{x03BC}\text{m}$
. After dispersion, the horizontal beam size increases to
![]() $\unicode[STIX]{x1D70E}_{T}=200~\unicode[STIX]{x03BC}\text{m}$
. The radiation power is improved by two orders of magnitude and reaches saturation with a properly dispersed
$\unicode[STIX]{x1D70E}_{T}=200~\unicode[STIX]{x03BC}\text{m}$
. The radiation power is improved by two orders of magnitude and reaches saturation with a properly dispersed
![]() $e$
beam, as shown in Figure 3(a). A single coherent spike is formed with a dispersed
$e$
beam, as shown in Figure 3(a). A single coherent spike is formed with a dispersed
![]() $e$
beam owing to the short duration of the beam, as shown in Figure 3(b). The transverse angular patterns for the cases without and with dispersion are shown in Figures 3(c) and 3(d).
$e$
beam owing to the short duration of the beam, as shown in Figure 3(b). The transverse angular patterns for the cases without and with dispersion are shown in Figures 3(c) and 3(d).

Figure 3. (a) Radiation power along the PU around 3.9 nm; (b) single-shot spectra of the SASE FEL; (c), (d) corresponding transverse angular profiles of the radiation power obtained by
![]() $e$
beam without and with the horizontal dispersion.
$e$
beam without and with the horizontal dispersion.
3 Analysis of radiation properties
According to the aforementioned discussion, the radiation properties can be significantly improved by utilizing a properly dispersed
![]() $e$
beam in the PU scheme. Taking the 30 nm radiation as an example, we now study the properties of the radiation with different dispersions of the
$e$
beam in the PU scheme. Taking the 30 nm radiation as an example, we now study the properties of the radiation with different dispersions of the
![]() $e$
beam. Figure 4(a) shows the radiation power at the exit of the undulator as a function of the transverse dispersion in both the PU and TGU schemes. The perfect-matching condition of
$e$
beam. Figure 4(a) shows the radiation power at the exit of the undulator as a function of the transverse dispersion in both the PU and TGU schemes. The perfect-matching condition of
![]() $\unicode[STIX]{x1D6FC}=(2+K_{0}^{2})/D_{x}K_{0}^{2}$
is satisfied in all of our simulation cases for the TGU scheme. The radiation power is significantly enhanced by introducing the
$\unicode[STIX]{x1D6FC}=(2+K_{0}^{2})/D_{x}K_{0}^{2}$
is satisfied in all of our simulation cases for the TGU scheme. The radiation power is significantly enhanced by introducing the
![]() $e$
-beam dispersion. As discussed previously, Equation (1) must be satisfied for obtaining a high-gain FEL. After the dispersion of the
$e$
-beam dispersion. As discussed previously, Equation (1) must be satisfied for obtaining a high-gain FEL. After the dispersion of the
![]() $e$
beam is introduced, the localized energy spread decreases, as does the effective FEL parameter. However, compared with the effective FEL parameter, the localized energy spread decreases rapidly as the dispersion increases, as indicated by Equations (2) and (3). Equation (1) can be satisfied when the horizontal dispersion is greater than a certain value, which results in the enhancement of the radiation power. Figure 4(a) indicates that the optimum dispersion region in the PU scheme differs from that in the TGU scheme and that the maximum radiation power in the PU scheme is approximated one order of magnitude lower than that in the TGU scheme. In our simulation cases in the last section, the dispersion is chosen to be 2.5 cm, which is the optimum dispersion for the PU scheme.
$e$
beam is introduced, the localized energy spread decreases, as does the effective FEL parameter. However, compared with the effective FEL parameter, the localized energy spread decreases rapidly as the dispersion increases, as indicated by Equations (2) and (3). Equation (1) can be satisfied when the horizontal dispersion is greater than a certain value, which results in the enhancement of the radiation power. Figure 4(a) indicates that the optimum dispersion region in the PU scheme differs from that in the TGU scheme and that the maximum radiation power in the PU scheme is approximated one order of magnitude lower than that in the TGU scheme. In our simulation cases in the last section, the dispersion is chosen to be 2.5 cm, which is the optimum dispersion for the PU scheme.

Figure 4. SASE FEL (a) radiation power, (b) bandwidth and (c) transverse mode parameter at 30 nm at the exit of the undulator with different dispersions of the
![]() $e$
beam in the PU (blue) and TGU (red) schemes.
$e$
beam in the PU (blue) and TGU (red) schemes.
Figure 4(b) shows the bandwidth of the FEL radiation at the exit of the undulator. The bandwidth decreases rapidly as the dispersion increases and then reaches its minimum value; after that, the bandwidth increases slowly as the dispersion increases in the PU scheme. To achieve the minimum value, the optimum dispersion is chosen to be 1 and 2.5 cm for the TGU and PU schemes, respectively, and the corresponding transverse gradient for the TGU scheme is 251.2 T/m. According to the resonant condition, the electrons that deviate from the transverse beam center cause a radiation wavelength shift, increasing the bandwidth. However, Figure 4(b) indicates that the bandwidth in the PU scheme is comparable to or even less than that in the TGU scheme in a certain range of the dispersion, which provides evidence that only part of the electrons near the beam center contribute to the radiation.
Because of the stronger diffraction and smaller spatial overlap with the
![]() $e$
beam, the higher-order modes can be suppressed. Thus, the SASE FEL can reach almost full transverse coherence before saturation, and the radiation emittance is almost given by the diffraction-limited radiation emittance
$e$
beam, the higher-order modes can be suppressed. Thus, the SASE FEL can reach almost full transverse coherence before saturation, and the radiation emittance is almost given by the diffraction-limited radiation emittance
![]() $\unicode[STIX]{x1D700}_{r0}=\unicode[STIX]{x1D706}_{1}/(4\unicode[STIX]{x1D70B})$
, where
$\unicode[STIX]{x1D700}_{r0}=\unicode[STIX]{x1D706}_{1}/(4\unicode[STIX]{x1D70B})$
, where
![]() $\unicode[STIX]{x1D706}_{1}$
is the resonant wavelength of the radiation. However, the large transverse beam size due to the dispersion provides enough transverse space for the high-order modes to couple with the
$\unicode[STIX]{x1D706}_{1}$
is the resonant wavelength of the radiation. However, the large transverse beam size due to the dispersion provides enough transverse space for the high-order modes to couple with the
![]() $e$
beam, reducing the transverse coherence. The transverse mode parameter can be defined as[Reference Huang and Kim21]
$e$
beam, reducing the transverse coherence. The transverse mode parameter can be defined as[Reference Huang and Kim21]
where
![]() $\unicode[STIX]{x1D700}_{r}=\unicode[STIX]{x1D70E}_{r}\unicode[STIX]{x1D70E}_{r^{\prime }}$
is the radiation emittance,
$\unicode[STIX]{x1D700}_{r}=\unicode[STIX]{x1D70E}_{r}\unicode[STIX]{x1D70E}_{r^{\prime }}$
is the radiation emittance,
![]() $\unicode[STIX]{x1D70E}_{r}$
and
$\unicode[STIX]{x1D70E}_{r}$
and
![]() $\unicode[STIX]{x1D70E}_{r^{\prime }}$
are the RMS radius and the far-field divergence half-angle of the radiation, respectively[Reference Vartanyants and Singer32]. Here, the RMS radius is defined as the second-order moment of light intensity and the evolution of the RMS radius is
$\unicode[STIX]{x1D70E}_{r^{\prime }}$
are the RMS radius and the far-field divergence half-angle of the radiation, respectively[Reference Vartanyants and Singer32]. Here, the RMS radius is defined as the second-order moment of light intensity and the evolution of the RMS radius is
![]() $\unicode[STIX]{x1D70E}_{r}^{2}(z)=\unicode[STIX]{x1D70E}_{r}^{2}(z_{0})+\unicode[STIX]{x1D70E}_{r^{\prime }}^{2}(z-z_{0})^{2}$
, where
$\unicode[STIX]{x1D70E}_{r}^{2}(z)=\unicode[STIX]{x1D70E}_{r}^{2}(z_{0})+\unicode[STIX]{x1D70E}_{r^{\prime }}^{2}(z-z_{0})^{2}$
, where
![]() $\unicode[STIX]{x1D70E}_{r}(z_{0})$
is the RMS waist radius[Reference Vartanyants and Singer32]. The transverse mode parameter is discussed only in the horizontal direction, owing to the horizontal dispersion. Figure 4(c) shows the transverse mode parameter as a function of the dispersions of the
$\unicode[STIX]{x1D70E}_{r}(z_{0})$
is the RMS waist radius[Reference Vartanyants and Singer32]. The transverse mode parameter is discussed only in the horizontal direction, owing to the horizontal dispersion. Figure 4(c) shows the transverse mode parameter as a function of the dispersions of the
![]() $e$
beam for both the PU and TGU schemes. Without the dispersion,
$e$
beam for both the PU and TGU schemes. Without the dispersion,
![]() $M_{T}^{2}\gg 1$
, indicating that the transverse coherence is poor. After the dispersion of the
$M_{T}^{2}\gg 1$
, indicating that the transverse coherence is poor. After the dispersion of the
![]() $e$
beam is introduced, the coherent properties are improved in both schemes. For obtaining the best transverse coherence of the radiation, the optimum dispersion is 1.5 and 2.5 cm for the TGU and PU scheme, respectively. Figure 4(c) indicates that the mode parameter in the PU scheme is lower than that in the TGU scheme when the dispersion is
$e$
beam is introduced, the coherent properties are improved in both schemes. For obtaining the best transverse coherence of the radiation, the optimum dispersion is 1.5 and 2.5 cm for the TGU and PU scheme, respectively. Figure 4(c) indicates that the mode parameter in the PU scheme is lower than that in the TGU scheme when the dispersion is
![]() ${\geqslant}2$
cm. That is, for the high-order modes, it is more difficult to couple with the
${\geqslant}2$
cm. That is, for the high-order modes, it is more difficult to couple with the
![]() $e$
beam in the PU scheme than in the TGU scheme when the horizontal dispersion is large, which may provide additional evidence that the radiation emitted by the center electrons dominates.
$e$
beam in the PU scheme than in the TGU scheme when the horizontal dispersion is large, which may provide additional evidence that the radiation emitted by the center electrons dominates.
4 Physical mechanism of proposed scheme
Consider an
![]() $e$
beam having a horizontal dispersion, whose phase-space distribution is schematically illustrated in Figure 1(c). In the start-up process, the radiation wavelength has a linear dependence on the horizontal position according to the resonant condition, and the gain is relatively low. As the radiation power increases, the center electrons start bunching owing to the highest localized density, which results in the exponential gain of the central-wavelength radiation. According to the resonant condition, the wavelength of the radiation emitted by the off-center electrons differs from the center wavelength in the PU scheme. Because of the interaction between the center-wavelength radiation and the off-center electrons, the bunching efficiency in the PU scheme is lower than that in the TGU scheme for the off-center electrons. This is equivalent to that the bunching efficiency is lower when the wavelength of the seed laser differs from the resonant wavelength than that situation when the seed wavelength equals the resonant wavelength of the undulator. The radiation emitted by the center electrons dominates; thus, the PU can be regarded as the filter for selecting the central electrons to achieve the radiation.
$e$
beam having a horizontal dispersion, whose phase-space distribution is schematically illustrated in Figure 1(c). In the start-up process, the radiation wavelength has a linear dependence on the horizontal position according to the resonant condition, and the gain is relatively low. As the radiation power increases, the center electrons start bunching owing to the highest localized density, which results in the exponential gain of the central-wavelength radiation. According to the resonant condition, the wavelength of the radiation emitted by the off-center electrons differs from the center wavelength in the PU scheme. Because of the interaction between the center-wavelength radiation and the off-center electrons, the bunching efficiency in the PU scheme is lower than that in the TGU scheme for the off-center electrons. This is equivalent to that the bunching efficiency is lower when the wavelength of the seed laser differs from the resonant wavelength than that situation when the seed wavelength equals the resonant wavelength of the undulator. The radiation emitted by the center electrons dominates; thus, the PU can be regarded as the filter for selecting the central electrons to achieve the radiation.
We now give a theoretical description of the radiation with a dispersed
![]() $e$
beam and compare between the PU and TGU schemes. A 3D theoretical model based on the analysis of the eigenmode was established in Ref. [Reference Baxevanis, Huang, Ruth and Schroeder33] to explain the properties of the FEL radiation. Each growth mode of the radiation, characterized by the transverse profile
$e$
beam and compare between the PU and TGU schemes. A 3D theoretical model based on the analysis of the eigenmode was established in Ref. [Reference Baxevanis, Huang, Ruth and Schroeder33] to explain the properties of the FEL radiation. Each growth mode of the radiation, characterized by the transverse profile
![]() $A(\boldsymbol{x})$
and the complex growth rate
$A(\boldsymbol{x})$
and the complex growth rate
![]() $\unicode[STIX]{x1D707}$
, has a solution of the form
$\unicode[STIX]{x1D707}$
, has a solution of the form
![]() $A(\boldsymbol{x})e^{i\unicode[STIX]{x1D707}z}$
. The growth rate with a negative imaginary part represents the growth mode. An analytical solution is obtained for the case where the transverse emittance and focusing are negligible (which is suitable for
$A(\boldsymbol{x})e^{i\unicode[STIX]{x1D707}z}$
. The growth rate with a negative imaginary part represents the growth mode. An analytical solution is obtained for the case where the transverse emittance and focusing are negligible (which is suitable for
![]() $e$
beams from an LWFA owing to the small emittance), and the scaled growth rate
$e$
beams from an LWFA owing to the small emittance), and the scaled growth rate
![]() $\hat{\unicode[STIX]{x1D707}}$
of a growing mode is obtained using the relation[Reference Baxevanis, Huang, Ruth and Schroeder33]
$\hat{\unicode[STIX]{x1D707}}$
of a growing mode is obtained using the relation[Reference Baxevanis, Huang, Ruth and Schroeder33]
 $$\begin{eqnarray}\displaystyle & & \displaystyle \hat{\unicode[STIX]{x1D707}}-\frac{i}{\sqrt{2}{\hat{w}}}\biggl[\left(2m+1\right)\sqrt{p_{dx}}\biggl(1-\frac{24\hat{p}_{0}^{2}}{{\hat{w}}^{2}}\biggr)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad +\,(2n+1)\sqrt{p_{dy}}\biggr]+\frac{8\hat{p}_{0}^{2}}{{\hat{w}}^{4}}\biggl(1-\frac{24\hat{p}_{0}^{2}}{{\hat{w}}^{2}}\biggr)^{-1}=-\frac{1}{{\hat{w}}^{2}}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \hat{\unicode[STIX]{x1D707}}-\frac{i}{\sqrt{2}{\hat{w}}}\biggl[\left(2m+1\right)\sqrt{p_{dx}}\biggl(1-\frac{24\hat{p}_{0}^{2}}{{\hat{w}}^{2}}\biggr)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad +\,(2n+1)\sqrt{p_{dy}}\biggr]+\frac{8\hat{p}_{0}^{2}}{{\hat{w}}^{4}}\biggl(1-\frac{24\hat{p}_{0}^{2}}{{\hat{w}}^{2}}\biggr)^{-1}=-\frac{1}{{\hat{w}}^{2}}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Here,
![]() $p_{dx}=(4\unicode[STIX]{x1D70C}_{T}k_{u}k_{r}\unicode[STIX]{x1D70E}_{T}^{2})^{-1}$
and
$p_{dx}=(4\unicode[STIX]{x1D70C}_{T}k_{u}k_{r}\unicode[STIX]{x1D70E}_{T}^{2})^{-1}$
and
![]() $p_{dy}=(4\unicode[STIX]{x1D70C}_{T}k_{u}k_{r}\unicode[STIX]{x1D70E}_{y}^{2})^{-1}$
are the diffraction parameters,
$p_{dy}=(4\unicode[STIX]{x1D70C}_{T}k_{u}k_{r}\unicode[STIX]{x1D70E}_{y}^{2})^{-1}$
are the diffraction parameters,
![]() $k_{u}=2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D706}_{u}$
,
$k_{u}=2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D706}_{u}$
,
![]() $k_{r}=2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D706}_{r}$
,
$k_{r}=2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D706}_{r}$
,
![]() $m$
and
$m$
and
![]() $n$
are the transverse mode numbers, and
$n$
are the transverse mode numbers, and
![]() ${\hat{w}}=\hat{\unicode[STIX]{x1D707}}-\hat{\unicode[STIX]{x1D708}}$
, where
${\hat{w}}=\hat{\unicode[STIX]{x1D707}}-\hat{\unicode[STIX]{x1D708}}$
, where
![]() $\hat{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D707}/\left(2\unicode[STIX]{x1D70C}_{T}k_{u}\right)$
and
$\hat{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D707}/\left(2\unicode[STIX]{x1D70C}_{T}k_{u}\right)$
and
![]() $\hat{\unicode[STIX]{x1D708}}=\unicode[STIX]{x0394}\unicode[STIX]{x1D708}/\left(2\unicode[STIX]{x1D70C}_{T}\right)$
are the scaled growth rate and the detuning parameter, respectively. Here,
$\hat{\unicode[STIX]{x1D708}}=\unicode[STIX]{x0394}\unicode[STIX]{x1D708}/\left(2\unicode[STIX]{x1D70C}_{T}\right)$
are the scaled growth rate and the detuning parameter, respectively. Here,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D708}$
is the dimensionless detuning variable which represents the normalized deviation of the radiation wavelength
$\unicode[STIX]{x0394}\unicode[STIX]{x1D708}$
is the dimensionless detuning variable which represents the normalized deviation of the radiation wavelength
![]() $\unicode[STIX]{x1D706}$
from the resonant wavelength
$\unicode[STIX]{x1D706}$
from the resonant wavelength
![]() $\unicode[STIX]{x1D706}_{1}$
according to Refs. [Reference Huang and Kim21, Reference Baxevanis, Huang, Ruth and Schroeder33].
$\unicode[STIX]{x1D706}_{1}$
according to Refs. [Reference Huang and Kim21, Reference Baxevanis, Huang, Ruth and Schroeder33].
![]() $p_{0}=\unicode[STIX]{x1D70E}_{T}C_{p}/\left(2\unicode[STIX]{x1D70C}_{T}D_{x}\right)$
is the scaled TGU resonant parameter, where
$p_{0}=\unicode[STIX]{x1D70E}_{T}C_{p}/\left(2\unicode[STIX]{x1D70C}_{T}D_{x}\right)$
is the scaled TGU resonant parameter, where
![]() $C_{p}=\unicode[STIX]{x1D70E}_{x}^{2}/\unicode[STIX]{x1D70E}_{T}^{2}$
when the resonant condition is satisfied. The effective operation of an FEL setup requires a significantly reduced effective energy spread; thus, we can make the large-dispersion approximate
$C_{p}=\unicode[STIX]{x1D70E}_{x}^{2}/\unicode[STIX]{x1D70E}_{T}^{2}$
when the resonant condition is satisfied. The effective operation of an FEL setup requires a significantly reduced effective energy spread; thus, we can make the large-dispersion approximate
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FF}}^{ef}=\unicode[STIX]{x1D70E}_{x}/D_{x}$
.
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FF}}^{ef}=\unicode[STIX]{x1D70E}_{x}/D_{x}$
.

Figure 5. Negative imaginary part of the FEL growth rate
![]() $\hat{\unicode[STIX]{x1D707}}$
(in units of
$\hat{\unicode[STIX]{x1D707}}$
(in units of
![]() $2\unicode[STIX]{x1D70C}_{T}k_{u}$
) as a function of the horizontal position (in units of
$2\unicode[STIX]{x1D70C}_{T}k_{u}$
) as a function of the horizontal position (in units of
![]() $\unicode[STIX]{x1D70E}_{T}$
) for both the PU and TGU schemes in the fundamental mode (
$\unicode[STIX]{x1D70E}_{T}$
) for both the PU and TGU schemes in the fundamental mode (
![]() $D_{x}=2.5$
cm).
$D_{x}=2.5$
cm).
The above theoretical analysis is based on the TGU scheme and cannot be directly applied to the PU scheme. From a local viewpoint, the wavelength of a photon emitted by an electron is determined by the energy of the electron, which follows the relation
![]() $\unicode[STIX]{x1D706}_{rad}=\unicode[STIX]{x1D706}_{u}(1+K_{0}^{2}/2)/2\unicode[STIX]{x1D6FE}^{2}$
. We make the simple assumption that
$\unicode[STIX]{x1D706}_{rad}=\unicode[STIX]{x1D706}_{u}(1+K_{0}^{2}/2)/2\unicode[STIX]{x1D6FE}^{2}$
. We make the simple assumption that
![]() $\hat{p}_{0}=0$
, which means that all the electrons satisfy the resonant condition under the large-dispersion approximation in both the PU and TGU schemes. However, the radiation wavelength shifts in the PU scheme when the energy of the electron deviates from
$\hat{p}_{0}=0$
, which means that all the electrons satisfy the resonant condition under the large-dispersion approximation in both the PU and TGU schemes. However, the radiation wavelength shifts in the PU scheme when the energy of the electron deviates from
![]() $\unicode[STIX]{x1D6FE}_{0}$
, which can be described by the frequency-detuning parameter
$\unicode[STIX]{x1D6FE}_{0}$
, which can be described by the frequency-detuning parameter
![]() $\hat{\unicode[STIX]{x1D708}}$
. The difference between the TGU and PU schemes is that the frequency detuning is independent upon the transverse position in the TGU when the matching condition is fulfilled (here, we set
$\hat{\unicode[STIX]{x1D708}}$
. The difference between the TGU and PU schemes is that the frequency detuning is independent upon the transverse position in the TGU when the matching condition is fulfilled (here, we set
![]() $\hat{\unicode[STIX]{x1D708}}=0$
under the large-dispersion approximation). In the PU scheme, the detuning increases when the electron deviates from the horizontal beam center. We define a detuning parameter in the PU scheme that depends on the horizontal position
$\hat{\unicode[STIX]{x1D708}}=0$
under the large-dispersion approximation). In the PU scheme, the detuning increases when the electron deviates from the horizontal beam center. We define a detuning parameter in the PU scheme that depends on the horizontal position
![]() $x$
:
$x$
:
By substituting Equation (7) into Equation (6), the normalized growth rate can be determined as a function of the horizontal position, as shown in Figure 5. A simulation is performed using the parameters shown in Table 1 with the
![]() $e$
-beam horizontal dispersion of 2.5 cm. For this dispersion value, the corresponding parameters are given as
$e$
-beam horizontal dispersion of 2.5 cm. For this dispersion value, the corresponding parameters are given as
![]() $p_{dx}=0.013$
,
$p_{dx}=0.013$
,
![]() $p_{dy}=2$
, and
$p_{dy}=2$
, and
![]() $\unicode[STIX]{x1D70E}_{T}/\unicode[STIX]{x1D70E}_{x}=12.4$
. The growth rate remains constant at any horizontal position in the TGU scheme and decreases when the electron deviates from the beam center in the PU scheme. Once the horizontal position of the electron exceeds the blue covered region shown in Figure 5, the growth mode changes to the decrease mode, in which the electrons do not contribute to the radiation. Only part of the electrons contribute to the radiation, but intense FEL radiation is obtained owing to the high-peak current of the
$\unicode[STIX]{x1D70E}_{T}/\unicode[STIX]{x1D70E}_{x}=12.4$
. The growth rate remains constant at any horizontal position in the TGU scheme and decreases when the electron deviates from the beam center in the PU scheme. Once the horizontal position of the electron exceeds the blue covered region shown in Figure 5, the growth mode changes to the decrease mode, in which the electrons do not contribute to the radiation. Only part of the electrons contribute to the radiation, but intense FEL radiation is obtained owing to the high-peak current of the
![]() $e$
beams from the LWFA.
$e$
beams from the LWFA.

Figure 6. (a) SASE FEL power with different halfwidths of the slit at the entrance of the undulator in the PU scheme. (b)–(e) Horizontal distribution of the radiation with different halfwidths of the slit in the PU scheme. The halfwidths of the slit are
![]() $0.5\unicode[STIX]{x1D70E}_{T}$
,
$0.5\unicode[STIX]{x1D70E}_{T}$
,
![]() $1.0\unicode[STIX]{x1D70E}_{T}$
,
$1.0\unicode[STIX]{x1D70E}_{T}$
,
![]() $1.5\unicode[STIX]{x1D70E}_{T}$
and
$1.5\unicode[STIX]{x1D70E}_{T}$
and
![]() $3\unicode[STIX]{x1D70E}_{T}$
, respectively. The horizontal dispersion is 2.5 cm.
$3\unicode[STIX]{x1D70E}_{T}$
, respectively. The horizontal dispersion is 2.5 cm.
The simulation results and theoretical analysis demonstrate that the significant fraction of the off-center electrons makes no contribution to the lasing in our proposed scheme. This mechanism is similar to the collimation of the energy tail. Next, we conduct simulations by adding a horizontal collimator with different widths of the slit at the entrance of the undulator to perform a comparison. The horizontal dispersion of the
![]() $e$
beam is
$e$
beam is
![]() $D_{x}=2.5$
cm. Figure 6(a) shows that the radiation power increases as the slit width increases when the halfwidth of the slit is
$D_{x}=2.5$
cm. Figure 6(a) shows that the radiation power increases as the slit width increases when the halfwidth of the slit is
![]() ${\leqslant}0.5\unicode[STIX]{x1D70E}_{T}$
. However, when the halfwidth of the slit exceeds
${\leqslant}0.5\unicode[STIX]{x1D70E}_{T}$
. However, when the halfwidth of the slit exceeds
![]() $0.5\unicode[STIX]{x1D70E}_{T}$
, the radiation power changes little with the increase of the slit width in the PU scheme. For the cases with the collimator (the halfwidth of the slit is
$0.5\unicode[STIX]{x1D70E}_{T}$
, the radiation power changes little with the increase of the slit width in the PU scheme. For the cases with the collimator (the halfwidth of the slit is
![]() $0.5\unicode[STIX]{x1D70E}_{T}$
) and without the collimator, the average radiation power is 84 and 90 MW, respectively, in the PU scheme. That is, approximately 37% of the electrons near the beam center contribute more than 90% of the total radiation power. Figures 6(b)–6(e) show the horizontal distribution of the radiation with different slit widths in the PU scheme. The horizontal profile remains stable as the slit width increases. These simulation results show remarkable agreement with our aforementioned theory.
$0.5\unicode[STIX]{x1D70E}_{T}$
) and without the collimator, the average radiation power is 84 and 90 MW, respectively, in the PU scheme. That is, approximately 37% of the electrons near the beam center contribute more than 90% of the total radiation power. Figures 6(b)–6(e) show the horizontal distribution of the radiation with different slit widths in the PU scheme. The horizontal profile remains stable as the slit width increases. These simulation results show remarkable agreement with our aforementioned theory.
5 Conclusions
Simulations demonstrate that the FEL performance can be significantly improved with a PU by introducing the horizontal dispersion of the
![]() $e$
beam from the LWFA. Although only part of the electrons near the beam center contribute to the radiation, intense FEL radiation can be obtained owing to the high-peak current of the
$e$
beam from the LWFA. Although only part of the electrons near the beam center contribute to the radiation, intense FEL radiation can be obtained owing to the high-peak current of the
![]() $e$
beam. The radiation pulses can be sub-gigawatt level in power with a narrow bandwidth below 1% and good transverse coherence without seeding. The proposed scheme is easy to implement, which is significant for the experimental realization of the LWFA-based FEL. Further investigations on driving short-wavelength LWFA-based FELs are ongoing.
$e$
beam. The radiation pulses can be sub-gigawatt level in power with a narrow bandwidth below 1% and good transverse coherence without seeding. The proposed scheme is easy to implement, which is significant for the experimental realization of the LWFA-based FEL. Further investigations on driving short-wavelength LWFA-based FELs are ongoing.
Acknowledgements
This research was funded by the National Natural Science Foundation of China (Nos. 11127901, 11425418, 61521093, and 11505263), the Shanghai Sailing Program (No. 18YF1426000), the Strategic Priority Research Program (B) (No. XDB16), the Youth Innovation Promotion Association CAS and the State Key Laboratory Program of the Chinese Ministry of Science and Technology.